No CrossRef data available.
Article contents
Phase retrieval on circles and lines
Published online by Cambridge University Press: 10 May 2024
Abstract
Let f and g be analytic functions on the open unit disk 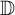 ${\mathbb D}$ such that
${\mathbb D}$ such that 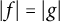 $|f|=|g|$ on a set A. We give an alternative proof of the result of Perez that there exists c in the unit circle
$|f|=|g|$ on a set A. We give an alternative proof of the result of Perez that there exists c in the unit circle 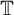 ${\mathbb T}$ such that
${\mathbb T}$ such that 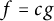 $f=cg$ when A is the union of two lines in
$f=cg$ when A is the union of two lines in 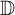 ${\mathbb D}$ intersecting at an angle that is an irrational multiple of
${\mathbb D}$ intersecting at an angle that is an irrational multiple of 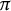 $\pi $, and from this, deduce a sequential generalization of the result. Similarly, the same conclusion is valid when f and g are in the Nevanlinna class and A is the union of the unit circle and an interior circle, tangential or not. We also provide sequential versions of this result and analyze the case
$\pi $, and from this, deduce a sequential generalization of the result. Similarly, the same conclusion is valid when f and g are in the Nevanlinna class and A is the union of the unit circle and an interior circle, tangential or not. We also provide sequential versions of this result and analyze the case 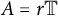 $A=r{\mathbb T}$. Finally, we examine the most general situation when there is equality on two distinct circles in the disk, proving a result or counterexample for each possible configuration.
$A=r{\mathbb T}$. Finally, we examine the most general situation when there is equality on two distinct circles in the disk, proving a result or counterexample for each possible configuration.
- Type
- Article
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press on behalf of Canadian Mathematical Society





