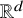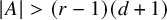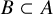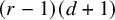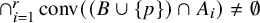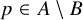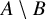1 Introduction
Let
![]() $\mathcal {F}$
be a family of (not necessarily distinct) sets, colored with r colors. Formally, we have a partition
$\mathcal {F}$
be a family of (not necessarily distinct) sets, colored with r colors. Formally, we have a partition
![]() $\mathcal {F}=\mathcal {F}_1\cup \cdots \cup \mathcal {F}_r$
. We call the subfamilies
$\mathcal {F}=\mathcal {F}_1\cup \cdots \cup \mathcal {F}_r$
. We call the subfamilies
![]() $\mathcal {F}_i$
the color classes of
$\mathcal {F}_i$
the color classes of
![]() $\mathcal {F}$
. We say that a subfamily
$\mathcal {F}$
. We say that a subfamily
![]() $\mathcal {F}'\subset \mathcal {F}$
is colorful if it contains at least one set from each color class. We say that
$\mathcal {F}'\subset \mathcal {F}$
is colorful if it contains at least one set from each color class. We say that
![]() $\mathcal {F}'$
is intersecting if
$\mathcal {F}'$
is intersecting if
![]() $\cap _{F\in \mathcal {F}'} F\neq \emptyset $
. The colorful Helly theorem, observed by Lovász, asserts the following:
$\cap _{F\in \mathcal {F}'} F\neq \emptyset $
. The colorful Helly theorem, observed by Lovász, asserts the following:
Theorem 1.1 (Lovász’s colorful Helly theorem (see [Reference Bárány4])).
Let
![]() $\mathcal {C}$
be a finite family of convex sets in
$\mathcal {C}$
be a finite family of convex sets in
![]() ${\mathbb R}^d$
colored with
${\mathbb R}^d$
colored with
![]() $d+1$
colors. If all colorful subfamilies of
$d+1$
colors. If all colorful subfamilies of
![]() $\mathcal {F}$
of size
$\mathcal {F}$
of size
![]() $d+1$
are intersecting, then one of the color classes is intersecting.
$d+1$
are intersecting, then one of the color classes is intersecting.
Many combinatorial properties of families of convex sets, and in particular Helly-type results like Theorem 1.1, can be described in terms of the nerve of the family. Given a finite family
![]() $\mathcal {F}$
of sets, the nerve of
$\mathcal {F}$
of sets, the nerve of
![]() $\mathcal {F}$
is the simplicial complex on vertex set
$\mathcal {F}$
is the simplicial complex on vertex set
![]() $\mathcal {F}$
whose simplices are the subfamilies
$\mathcal {F}$
whose simplices are the subfamilies
![]() $\mathcal {F}'\subset \mathcal {F}$
that are intersecting. We say that a simplicial complex X is d-representable if it is isomorphic to the nerve of some family of convex sets in
$\mathcal {F}'\subset \mathcal {F}$
that are intersecting. We say that a simplicial complex X is d-representable if it is isomorphic to the nerve of some family of convex sets in
![]() ${\mathbb R}^d$
.
${\mathbb R}^d$
.
Two related notions are those of d-collapsibility and d-Lerayness, introduced by Wegner in [Reference Wegner24]. Let X be a simplicial complex. A simplex
![]() $\sigma \in X$
is called a free face of X if
$\sigma \in X$
is called a free face of X if
![]() $\sigma $
is contained in a unique maximal face
$\sigma $
is contained in a unique maximal face
![]() $\tau $
(possibly equal to
$\tau $
(possibly equal to
![]() $\sigma $
) of X. Given a free face
$\sigma $
) of X. Given a free face
![]() $\sigma $
of size at most d in X, an elementary d-collapse is the operation of removing from X all the simplices containing
$\sigma $
of size at most d in X, an elementary d-collapse is the operation of removing from X all the simplices containing
![]() $\sigma $
(and contained in
$\sigma $
(and contained in
![]() $\tau $
). We say that X is d-collapsible if there is a sequence of elementary d-collapses reducing X to the void complex
$\tau $
). We say that X is d-collapsible if there is a sequence of elementary d-collapses reducing X to the void complex
![]() $\emptyset $
. A simplicial complex X is called d-Leray if all induced subcomplexes of X, including X itself, have trivial homology groups in dimensions d and higher.
$\emptyset $
. A simplicial complex X is called d-Leray if all induced subcomplexes of X, including X itself, have trivial homology groups in dimensions d and higher.
Wegner showed in [Reference Wegner24] that every d-representable complex is d-collapsible and that every d-collapsible complex is d-Leray. Many interesting results about the intersection patterns of a family of convex sets can be obtained from the fact that the nerve of such a family is d-collapsible (or d-Leray). For example, in [Reference Kalai and Meshulam9], Kalai and Meshulam proved the following generalizations of Theorem 1.1.
Theorem 1.2 [Reference Kalai and Meshulam9, Theorem 2.1].
Let X be a d-collapsible simplicial complex on vertex set V, and let M be a matroid on V of rank r, with rank function
![]() $\rho $
such that
$\rho $
such that
![]() $M\subset X$
. Then, there is some
$M\subset X$
. Then, there is some
![]() $\tau \in X$
such that
$\tau \in X$
such that
![]() $\rho (\tau )=r$
and
$\rho (\tau )=r$
and
![]() $\rho (V\setminus \tau )\leq d$
.
$\rho (V\setminus \tau )\leq d$
.
Theorem 1.3 [Reference Kalai and Meshulam9, Theorem 1.6].
Let X be a d-Leray simplicial complex on vertex set V, and let M be a matroid on V of rank r, with rank function
![]() $\rho $
such that
$\rho $
such that
![]() $M\subset X$
. Then, there is some
$M\subset X$
. Then, there is some
![]() $\tau \in X$
such that
$\tau \in X$
such that
![]() $\rho (V\setminus \tau )\leq d$
.
$\rho (V\setminus \tau )\leq d$
.
Theorem 1.1 can be deduced from either Theorem 1.2 or 1.3 by taking X to be the nerve of the family of convex sets, and M to be a ‘partition matroid’ corresponding to the coloring of the family (see Section 6 for more details).
Generalizations of Theorem 1.1 in a different direction were presented by Arocha et al. in [Reference Arocha, Bárány, Bracho, Fabila and Montejano3] and by Montejano and Karasev in [Reference Montejano and Karasev13].
Theorem 1.4 (Very colorful Helly theorem [Reference Arocha, Bárány, Bracho, Fabila and Montejano3, Theorem 10]).
Let
![]() $1\leq k\leq d+1$
, and let
$1\leq k\leq d+1$
, and let
![]() $\mathcal {C}$
be a finite family of convex sets in
$\mathcal {C}$
be a finite family of convex sets in
![]() ${\mathbb R}^d$
colored with
${\mathbb R}^d$
colored with
![]() $d+1$
colors. If every subfamily
$d+1$
colors. If every subfamily
![]() $\mathcal {C}'\subset \mathcal {C}$
of size
$\mathcal {C}'\subset \mathcal {C}$
of size
![]() $d+1$
having at least k different colors is intersecting, then there are
$d+1$
having at least k different colors is intersecting, then there are
![]() $d+2-k$
color classes whose union is intersecting.
$d+2-k$
color classes whose union is intersecting.
Theorem 1.5 (‘Semi-intersecting’ colorful Helly theorem [Reference Montejano and Karasev13, Lemma 2]).
Let
![]() $\mathcal {C}$
be a finite family of convex sets in
$\mathcal {C}$
be a finite family of convex sets in
![]() ${\mathbb R}^d$
colored with
${\mathbb R}^d$
colored with
![]() $d+2$
colors. If every colorful subfamily of size
$d+2$
colors. If every colorful subfamily of size
![]() $d+2$
has at most one nonintersecting subfamily of size
$d+2$
has at most one nonintersecting subfamily of size
![]() $d+1$
, then one of the color classes is intersecting.
$d+1$
, then one of the color classes is intersecting.
Our main results consist of the following common generalizations of Theorem 1.4, Theorem 1.5 and Theorem 1.2 (Theorem 1.3, respectively).
Theorem 1.6. Let
![]() $d\geq 1$
,
$d\geq 1$
,
![]() $r\geq d+1$
,
$r\geq d+1$
,
![]() $1\leq m\leq r$
and
$1\leq m\leq r$
and
![]() $m\leq k\leq \min \{m+d,r\}$
be integers. Let V be a finite set with
$m\leq k\leq \min \{m+d,r\}$
be integers. Let V be a finite set with
![]() $|V|\geq \max \{m+d,r\}$
. Let X be a d-collapsible simplicial complex on vertex set V, and let M be a matroid of rank r on vertex set V with rank function
$|V|\geq \max \{m+d,r\}$
. Let X be a d-collapsible simplicial complex on vertex set V, and let M be a matroid of rank r on vertex set V with rank function
![]() $\rho $
.
$\rho $
.
Assume that, for every
![]() $U=\{u_1,\ldots ,u_d,v_1,\ldots ,v_m\}\subset V$
with
$U=\{u_1,\ldots ,u_d,v_1,\ldots ,v_m\}\subset V$
with
![]() $\rho (U)\geq k$
, there is some
$\rho (U)\geq k$
, there is some
![]() $i\in [m]$
such that
$i\in [m]$
such that
![]() $\{u_1,\ldots ,u_d,v_i\}\in X$
. Then, there is some
$\{u_1,\ldots ,u_d,v_i\}\in X$
. Then, there is some
![]() $\tau \in X$
such that
$\tau \in X$
such that
![]() $\rho (\tau )\geq r+1-m$
and
$\rho (\tau )\geq r+1-m$
and
![]() $\rho (V\setminus \tau )\leq k-1$
.
$\rho (V\setminus \tau )\leq k-1$
.
Under the weaker assumption of d-Lerayness, we obtain a weaker conclusion:
Theorem 1.7. Let
![]() $d\geq 1$
,
$d\geq 1$
,
![]() $r\geq d+1$
,
$r\geq d+1$
,
![]() $1\leq m\leq r$
and
$1\leq m\leq r$
and
![]() $m\leq k\leq \min \{m+d,r\}$
be integers. Let V be a finite set with
$m\leq k\leq \min \{m+d,r\}$
be integers. Let V be a finite set with
![]() $|V|\geq \max \{m+d,r\}$
. Let X be a d-Leray simplicial complex on vertex set V, and let M be a matroid of rank r on vertex set V with rank function
$|V|\geq \max \{m+d,r\}$
. Let X be a d-Leray simplicial complex on vertex set V, and let M be a matroid of rank r on vertex set V with rank function
![]() $\rho $
.
$\rho $
.
Assume that for every
![]() $U=\{u_1,\ldots ,u_{d+1},v_1,\ldots ,v_{m-1}\}\subset V$
with
$U=\{u_1,\ldots ,u_{d+1},v_1,\ldots ,v_{m-1}\}\subset V$
with
![]() $\rho (U)\geq k$
, either
$\rho (U)\geq k$
, either
![]() $\{u_1,\ldots ,u_{d+1}\}\in X$
or there exists
$\{u_1,\ldots ,u_{d+1}\}\in X$
or there exists
![]() $j\in [m-1]$
such that
$j\in [m-1]$
such that
![]() $\sigma \cup \{v_j\}\in X$
for every
$\sigma \cup \{v_j\}\in X$
for every
![]() $\sigma \subsetneq \{u_1,\ldots ,u_{d+1}\}$
. Then, there is some
$\sigma \subsetneq \{u_1,\ldots ,u_{d+1}\}$
. Then, there is some
![]() $\tau \in X$
such that
$\tau \in X$
such that
![]() $\rho (V\setminus \tau ) \leq k-1$
.
$\rho (V\setminus \tau ) \leq k-1$
.
Remark 1.8. Note that the condition in Theorem 1.6 is implied by the condition in Theorem 1.7 and that both conditions are implied by the following stronger (but perhaps more natural) condition: ‘For every subset U of V of size
![]() $d+m$
with
$d+m$
with
![]() $\rho (U) \geq k$
, all but possibly at most
$\rho (U) \geq k$
, all but possibly at most
![]() $m-1$
of the the subsets of U of size
$m-1$
of the the subsets of U of size
![]() $d+1$
are simplices in X’. Moreover, note that all three conditions are equivalent for
$d+1$
are simplices in X’. Moreover, note that all three conditions are equivalent for
![]() $m\leq 2$
.
$m\leq 2$
.
As an immediate consequence of Theorem 1.6, we obtain the following:
Theorem 1.9. Let
![]() $d\geq 1$
,
$d\geq 1$
,
![]() $r\geq d+1$
,
$r\geq d+1$
,
![]() $1\leq m\leq r$
and
$1\leq m\leq r$
and
![]() $m\leq k\leq \min \{m+d,r\}$
. Let
$m\leq k\leq \min \{m+d,r\}$
. Let
![]() $\mathcal {C}$
be a finite family of convex sets in
$\mathcal {C}$
be a finite family of convex sets in
![]() ${\mathbb R}^d$
, colored with r different colors, of size
${\mathbb R}^d$
, colored with r different colors, of size
![]() $|\mathcal {C}|\geq \max \{m+d,r\}$
. Assume that for every family
$|\mathcal {C}|\geq \max \{m+d,r\}$
. Assume that for every family
![]() $\{A_1,\ldots ,A_d,B_1,\ldots ,B_m\}\subset \mathcal {C}$
, colored with at least k different colors, at least one of the subfamilies of the form
$\{A_1,\ldots ,A_d,B_1,\ldots ,B_m\}\subset \mathcal {C}$
, colored with at least k different colors, at least one of the subfamilies of the form
![]() $\{A_1,\ldots ,A_d,B_i\}$
, for
$\{A_1,\ldots ,A_d,B_i\}$
, for
![]() $i\in [m]$
, is intersecting. Then, there are
$i\in [m]$
, is intersecting. Then, there are
![]() $r-k+1$
color classes whose union is intersecting.
$r-k+1$
color classes whose union is intersecting.
In the special case
![]() $m=1$
and
$m=1$
and
![]() $r=d+1$
, we recover Theorem 1.4. For
$r=d+1$
, we recover Theorem 1.4. For
![]() $m=2$
and
$m=2$
and
![]() $r=k=d+2$
, we recover Theorem 1.5.
$r=k=d+2$
, we recover Theorem 1.5.
As an application of Theorem 1.9, we obtain the following extension of Tverberg’s theorem [Reference Tverberg23].
Let
![]() $A\subset {\mathbb R}^d$
be a finite set of points, and let
$A\subset {\mathbb R}^d$
be a finite set of points, and let
![]() $A=A_1\cup \ldots \cup A_r$
be a partition of A. We say that
$A=A_1\cup \ldots \cup A_r$
be a partition of A. We say that
![]() $A_1,\ldots , A_r$
is a Tverberg partition of A if
$A_1,\ldots , A_r$
is a Tverberg partition of A if
![]() $\cap _{i=1}^r \operatorname {\mathrm {\text {conv}}}(A_i)\neq \emptyset $
. Let
$\cap _{i=1}^r \operatorname {\mathrm {\text {conv}}}(A_i)\neq \emptyset $
. Let
![]() $B\subset A$
. We say that
$B\subset A$
. We say that
![]() $B\subsetneq A$
is a Tverberg center for the partition
$B\subsetneq A$
is a Tverberg center for the partition
![]() $A=A_1\cup \cdots \cup A_r$
if, for every
$A=A_1\cup \cdots \cup A_r$
if, for every
![]() $p\in A\setminus B$
,
$p\in A\setminus B$
,
![]() $ \bigcap _{i=1}^r \operatorname {\mathrm {\text {conv}}}\left ((B\cup \{p\})\cap A_i\right )\neq \emptyset. $
In other words, B is a Tverberg center for
$ \bigcap _{i=1}^r \operatorname {\mathrm {\text {conv}}}\left ((B\cup \{p\})\cap A_i\right )\neq \emptyset. $
In other words, B is a Tverberg center for
![]() $A=A_1\cup \ldots \cup A_r$
if, for every
$A=A_1\cup \ldots \cup A_r$
if, for every
![]() $p\in A\setminus B$
, the partition of
$p\in A\setminus B$
, the partition of
![]() $B\cup \{p\}$
induced by
$B\cup \{p\}$
induced by
![]() $A_1,\ldots ,A_r$
is a Tverberg partition.
$A_1,\ldots ,A_r$
is a Tverberg partition.
Theorem 1.10. Let
![]() $d\geq 1$
,
$d\geq 1$
,
![]() $r\geq 2$
, and let
$r\geq 2$
, and let
![]() $n=(r-1)(d+1)$
. Let
$n=(r-1)(d+1)$
. Let
![]() $A\subset {\mathbb R}^d$
be a finite set of points of size larger than n. Then, there exists a partition
$A\subset {\mathbb R}^d$
be a finite set of points of size larger than n. Then, there exists a partition
![]() $A_1,\ldots ,A_r$
of A that has a Tverberg center of size n.
$A_1,\ldots ,A_r$
of A that has a Tverberg center of size n.
For
![]() $|A|=n+1$
, this is exactly Tverberg’s theorem. Theorem 1.10 is sharp in the sense that we cannot guarantee a Tverberg center of size smaller than
$|A|=n+1$
, this is exactly Tverberg’s theorem. Theorem 1.10 is sharp in the sense that we cannot guarantee a Tverberg center of size smaller than
![]() $(r-1)(d+1)$
: Let A be a generic set of points in
$(r-1)(d+1)$
: Let A be a generic set of points in
![]() ${\mathbb R}^d$
(in the sense that the
${\mathbb R}^d$
(in the sense that the
![]() $d|A|$
coordinates of A are algebraically independent over the rationals). Assume for contradiction that A has a partition
$d|A|$
coordinates of A are algebraically independent over the rationals). Assume for contradiction that A has a partition
![]() $A_1,\ldots , A_r$
with a Tverberg center B of size
$A_1,\ldots , A_r$
with a Tverberg center B of size
![]() $k<(r-1)(d+1)$
. Then, for every
$k<(r-1)(d+1)$
. Then, for every
![]() $p\in A\setminus B$
,
$p\in A\setminus B$
,
![]() $B'=B\cup \{p\}$
is a generic set of
$B'=B\cup \{p\}$
is a generic set of
![]() $k+1\leq (r-1)(d+1)$
points in
$k+1\leq (r-1)(d+1)$
points in
![]() ${\mathbb R}^d$
, with a Tverberg partition into r parts. However, it is well known that such a set does not have a Tverberg partition into r parts (see, e.g., [Reference Tverberg23]). In fact, the condition of genericity can be replaced by the weaker property of ‘strong general position’ introduced by Reay in [Reference Reay18] (under the name ‘strong independence’); see also [Reference Perles and Sigron16, Reference Perles and Sigron17].
${\mathbb R}^d$
, with a Tverberg partition into r parts. However, it is well known that such a set does not have a Tverberg partition into r parts (see, e.g., [Reference Tverberg23]). In fact, the condition of genericity can be replaced by the weaker property of ‘strong general position’ introduced by Reay in [Reference Reay18] (under the name ‘strong independence’); see also [Reference Perles and Sigron16, Reference Perles and Sigron17].
Theorem 1.10 is closely related to the ‘tolerant Tverberg theorem’ (see, e.g., [Reference Larman12, Reference García-Colín6, Reference Soberón and Strausz21, Reference García-Colín and Larman7, Reference García-Colín, Raggi and Roldán-Pensado8]). Using Theorem 1.10, we obtain a new proof of the following result from [Reference Soberón and Strausz21]:
Theorem 1.11 (Soberón–Strausz [Reference Soberón and Strausz21, Theorem 1]).
Let
![]() $d\geq 1$
,
$d\geq 1$
,
![]() $r\geq 2$
and
$r\geq 2$
and
![]() $t\geq 0$
. Let
$t\geq 0$
. Let
![]() $A\subset {\mathbb R}^d$
be a finite set of points of size at least
$A\subset {\mathbb R}^d$
be a finite set of points of size at least
![]() $(t+1)(r-1)(d+1)+1$
. Then, there exists a partition
$(t+1)(r-1)(d+1)+1$
. Then, there exists a partition
![]() $A_1,\ldots ,A_r$
of A such that, for any
$A_1,\ldots ,A_r$
of A such that, for any
![]() $C\subset A$
of size t,
$C\subset A$
of size t,
 $$\begin{align*}\bigcap_{i=1}^r \operatorname{\mathrm{\text{conv}}}(A_i\setminus C)\neq\emptyset. \end{align*}$$
$$\begin{align*}\bigcap_{i=1}^r \operatorname{\mathrm{\text{conv}}}(A_i\setminus C)\neq\emptyset. \end{align*}$$
Our paper is organized as follows. In Section 2, we present some basic facts about simplicial complexes and matroids that we will use later. In Section 3, we introduce the notion of ‘tolerance complexes’ of matroids, which is used in the proofs of our main results. In Section 4, we present the proof of Theorem 1.6, and in Section 5, we present the proof of Theorem 1.7. Section 6 deals with the geometric applications of our results and contains the proofs of Theorems 1.9, 1.10 and 1.11. We conclude in Section 7 with some open problems arising from our work.
2 Preliminaries
2.1 Simplicial complexes
A simplicial complex X is a family of subsets of some finite set V such that for every
![]() $\sigma \in X$
and
$\sigma \in X$
and
![]() $\sigma '\subset \sigma $
, we have
$\sigma '\subset \sigma $
, we have
![]() $\sigma '\in X$
. The set
$\sigma '\in X$
. The set
![]() $V = V(X)$
is called the vertex set of X. The sets in X are called the simplices or faces of the complex. The dimension of a simplex
$V = V(X)$
is called the vertex set of X. The sets in X are called the simplices or faces of the complex. The dimension of a simplex
![]() $\sigma \in X$
is
$\sigma \in X$
is
![]() $|\sigma |-1$
, and the dimension of X, denoted by
$|\sigma |-1$
, and the dimension of X, denoted by
![]() $\dim (X)$
, is the maximal dimension of a simplex in X. We denote by
$\dim (X)$
, is the maximal dimension of a simplex in X. We denote by
![]() $2^V=\{\sigma :\, \sigma \subset U\}$
the complete complex on vertex set V.
$2^V=\{\sigma :\, \sigma \subset U\}$
the complete complex on vertex set V.
A subcomplex of X is a simplicial complex
![]() $X'$
such that each simplex of
$X'$
such that each simplex of
![]() $X'$
is also a simplex of X. For
$X'$
is also a simplex of X. For
![]() $U\subset V$
, the subcomplex of X induced by U is the complex
$U\subset V$
, the subcomplex of X induced by U is the complex
Let
![]() $\sigma $
be a simplex in X. We define the link of
$\sigma $
be a simplex in X. We define the link of
![]() $\sigma $
in X to be the subcomplex
$\sigma $
in X to be the subcomplex
and the costar of
![]() $\sigma $
in X to be the subcomplex
$\sigma $
in X to be the subcomplex
If
![]() $\sigma $
is a zero-dimensional simplex, that is, if
$\sigma $
is a zero-dimensional simplex, that is, if
![]() $\sigma = \{v\}$
for some vertex
$\sigma = \{v\}$
for some vertex
![]() $v \in V$
, we simply write
$v \in V$
, we simply write
![]() $\operatorname {\mathrm {lk}}(X,v)=\operatorname {\mathrm {lk}}(X,\{v\})$
, and
$\operatorname {\mathrm {lk}}(X,v)=\operatorname {\mathrm {lk}}(X,\{v\})$
, and
![]() $X\setminus v= \operatorname {\mathrm {cost}}(X,\{v\})=X[V\setminus \{v\}]$
.
$X\setminus v= \operatorname {\mathrm {cost}}(X,\{v\})=X[V\setminus \{v\}]$
.
Let X and Y be simplicial complexes on disjoint vertex sets. The join of X and Y is the simplicial complex on
![]() $V(X) \cup V(Y)$
defined as
$V(X) \cup V(Y)$
defined as
The following well-known special case of the Mayer–Vietoris exact sequence relates the homology of a complex X to that of the link and costar of one of its vertices (see, e.g., [Reference Kim and Lew11, Theorem 2.2] for a detailed proof).
Theorem 2.1. Let X be a simplicial complex on vertex set V, and let
![]() $v\in V$
. Then, there is an exact sequence
$v\in V$
. Then, there is an exact sequence
We will need the following equivalent definition of d-Leray complexes due to Kalai and Meshulam.
Lemma 2.2 [Reference Kalai and Meshulam10, Proposition 3.1].
A simplicial complex X is d-Leray if and only if
![]() $\tilde {H}_k(\operatorname {\mathrm {lk}}(X,\sigma ))=0$
for all
$\tilde {H}_k(\operatorname {\mathrm {lk}}(X,\sigma ))=0$
for all
![]() $\sigma \in X$
and
$\sigma \in X$
and
![]() $k\geq d$
.
$k\geq d$
.
Recall that, given a free face
![]() $\sigma \in X$
of size
$\sigma \in X$
of size
![]() $|\sigma |\leq d$
, an elementary d-collapse is the operation consisting of removing
$|\sigma |\leq d$
, an elementary d-collapse is the operation consisting of removing
![]() $\sigma $
and all simplices containing it from X. Note that the complex obtained after this operation is exactly
$\sigma $
and all simplices containing it from X. Note that the complex obtained after this operation is exactly
![]() $\operatorname {\mathrm {cost}}(X,\sigma )$
. We denote such an elementary d-collapse by
$\operatorname {\mathrm {cost}}(X,\sigma )$
. We denote such an elementary d-collapse by
![]() $X\to X'=\operatorname {\mathrm {cost}}(X,\sigma )$
. The following equivalent definition of d-collapsibility was observed by Tancer in [Reference Tancer22] (see also [Reference Wegner24, Lemma 1] for a similar statement):
$X\to X'=\operatorname {\mathrm {cost}}(X,\sigma )$
. The following equivalent definition of d-collapsibility was observed by Tancer in [Reference Tancer22] (see also [Reference Wegner24, Lemma 1] for a similar statement):
Lemma 2.3 [Reference Tancer22, Lemma 5.2].
A simplicial complex X is d-collapsible if and only if there is a sequence of elementary d-collapses
such that the free face in each elementary d-collapse is of size exactly d, and
![]() $\dim (X_t)< d-1$
.
$\dim (X_t)< d-1$
.
2.2 Matroids
A family M of subsets of a nonempty set V is a matroid if it satisfies
-
(i)
 $\emptyset \in M$
,
$\emptyset \in M$
, -
(ii) for all
 $A' \subset A \subset V$
, if
$A' \subset A \subset V$
, if
 $A \in M$
, then
$A \in M$
, then
 $A' \in M$
, and
$A' \in M$
, and -
(iii) if
 $A, B \in M$
and
$A, B \in M$
and
 $|A| < |B|$
, then there exists
$|A| < |B|$
, then there exists
 $x \in B \setminus A$
such that
$x \in B \setminus A$
such that
 $A \cup \{x\} \in M$
.
$A \cup \{x\} \in M$
.
The elements of M are usually called the independent sets of M, and the maximal elements are called the bases of M. The rank function of a matroid M on V is a function
![]() $\rho : 2^V \to \mathbb {N}$
such that for every
$\rho : 2^V \to \mathbb {N}$
such that for every
![]() $W \subset V$
,
$W \subset V$
,
![]() $\rho (W)$
equals the maximal size of a set
$\rho (W)$
equals the maximal size of a set
![]() $W' \subset W$
with
$W' \subset W$
with
![]() $W' \in M$
. The rank of the matroid M is defined as
$W' \in M$
. The rank of the matroid M is defined as
![]() $\rho (V)$
. The span of a set
$\rho (V)$
. The span of a set
![]() $U\subset V$
is defined as
$U\subset V$
is defined as
Note that the conditions (i) and (ii) allow us to regard a matroid M as a simplicial complex. Moreover, condition (iii), sometimes called the ‘exchange property’ for independent sets, implies that M is a pure simplicial complex – that is, all the bases of M are of the same size (equal to the rank of M). See, for example, [Reference Oxley15] for more background on matroids.
We will need the following very simple auxiliary results about matroids.
Lemma 2.4. Let M be a rank r matroid on vertex set V, and let
![]() $\rho $
be its rank function. Then, for each
$\rho $
be its rank function. Then, for each
![]() $0\leq t\leq |V|$
, there exists
$0\leq t\leq |V|$
, there exists
![]() $U\subset V$
such that
$U\subset V$
such that
![]() $|U|=t$
and
$|U|=t$
and
![]() $\rho (U)\geq \min \{t,r\}$
.
$\rho (U)\geq \min \{t,r\}$
.
Proof. If
![]() $t\leq r$
, let U be any independent set of M of size t. If
$t\leq r$
, let U be any independent set of M of size t. If
![]() $t\geq r$
, let
$t\geq r$
, let
![]() $U\subset V$
be any set of size t containing a basis of M.
$U\subset V$
be any set of size t containing a basis of M.
Lemma 2.5. Let M be a matroid on vertex set V with rank function
![]() $\rho $
. Let
$\rho $
. Let
![]() $U\subset W\subset V$
. Then
$U\subset W\subset V$
. Then
Proof. By definition of the rank function, W contains an independent set
![]() $W'$
of size
$W'$
of size
![]() $\rho (W)$
. Then,
$\rho (W)$
. Then,
![]() $W'\cap U$
is an independent set of size at least
$W'\cap U$
is an independent set of size at least
![]() $|W'|-|W\setminus U|=\rho (W)-|W\setminus U|$
. So
$|W'|-|W\setminus U|=\rho (W)-|W\setminus U|$
. So
![]() $\rho (U)\geq \rho (W)-|W\setminus U|$
.
$\rho (U)\geq \rho (W)-|W\setminus U|$
.
3 Tolerance complexes of matroids
Let M be a matroid with rank function
![]() $\rho $
on vertex set V. Let
$\rho $
on vertex set V. Let
![]() $r=\rho (V)$
be the rank of M. For
$r=\rho (V)$
be the rank of M. For
![]() $0\leq t\leq r$
, let
$0\leq t\leq r$
, let
In particular, for
![]() $t=0$
we have
$t=0$
we have
![]() $M^0=M$
. Note that
$M^0=M$
. Note that
![]() $M^t$
is exactly the ‘t-tolerance complex’ of M, as defined in [Reference Kim and Lew11].
$M^t$
is exactly the ‘t-tolerance complex’ of M, as defined in [Reference Kim and Lew11].
Lemma 3.1. Let
![]() $0\leq t\leq r$
. Then,
$0\leq t\leq r$
. Then,
![]() $M^t$
is a matroid.
$M^t$
is a matroid.
Proof. First, note that
![]() $M^t$
is a simplicial complex: If
$M^t$
is a simplicial complex: If
![]() $\sigma \in M^t$
and
$\sigma \in M^t$
and
![]() $\sigma '\subset \sigma $
, then, by Lemma 2.5,
$\sigma '\subset \sigma $
, then, by Lemma 2.5,
and therefore
![]() $\sigma '\in M^t$
.
$\sigma '\in M^t$
.
We will show that
![]() $M^t$
satisfies the exchange property for independent sets: Let
$M^t$
satisfies the exchange property for independent sets: Let
![]() $\sigma ,\tau \in M^t$
such that
$\sigma ,\tau \in M^t$
such that
![]() $|\tau |>|\sigma |$
. We have to show that there is a vertex
$|\tau |>|\sigma |$
. We have to show that there is a vertex
![]() $v\in \tau \setminus \sigma $
such that
$v\in \tau \setminus \sigma $
such that
![]() $\sigma \cup \{v\}\in M^t$
.
$\sigma \cup \{v\}\in M^t$
.
Since
![]() $\sigma \in M^t$
, we have
$\sigma \in M^t$
, we have
![]() $\rho (\sigma )\geq |\sigma |-t$
. If
$\rho (\sigma )\geq |\sigma |-t$
. If
![]() $\rho (\sigma )>|\sigma |-t$
, then for all
$\rho (\sigma )>|\sigma |-t$
, then for all
![]() $v\in V\setminus \sigma $
we have
$v\in V\setminus \sigma $
we have
![]() $\rho (\sigma \cup \{v\})\geq \rho (\sigma ) \geq |\sigma \cup \{v\}|-t$
, as wanted. If
$\rho (\sigma \cup \{v\})\geq \rho (\sigma ) \geq |\sigma \cup \{v\}|-t$
, as wanted. If
![]() $\rho (\sigma )=|\sigma |-t$
, then, since
$\rho (\sigma )=|\sigma |-t$
, then, since
![]() $\tau \in M^t$
,
$\tau \in M^t$
,
Let
![]() $\tau '\subset \tau $
such that
$\tau '\subset \tau $
such that
![]() $|\tau '|=\rho (\tau )$
and
$|\tau '|=\rho (\tau )$
and
![]() $\tau '\in M$
, and let
$\tau '\in M$
, and let
![]() $\sigma '\subset \sigma $
such that
$\sigma '\subset \sigma $
such that
![]() $|\sigma '|=\rho (\sigma )$
and
$|\sigma '|=\rho (\sigma )$
and
![]() $\sigma '\in M$
. Then, since
$\sigma '\in M$
. Then, since
![]() $|\tau '|>|\sigma '|$
, there exists
$|\tau '|>|\sigma '|$
, there exists
![]() $v\in \tau '\setminus \sigma '$
such that
$v\in \tau '\setminus \sigma '$
such that
![]() $\sigma '\cup \{v\}\in M$
. Note that
$\sigma '\cup \{v\}\in M$
. Note that
![]() $v\in \tau \setminus \sigma $
(otherwise,
$v\in \tau \setminus \sigma $
(otherwise,
![]() $\sigma '\cup \{v\}\subset \sigma $
, in contradiction to
$\sigma '\cup \{v\}\subset \sigma $
, in contradiction to
![]() $\rho (\sigma )=|\sigma '|$
). We obtain
$\rho (\sigma )=|\sigma '|$
). We obtain
and therefore,
![]() $\sigma \cup \{v\}\in M^t$
. Hence,
$\sigma \cup \{v\}\in M^t$
. Hence,
![]() $M^t$
is a matroid.
$M^t$
is a matroid.
Lemma 3.2. Let
![]() $0\leq t\leq r$
. Denote the rank function of
$0\leq t\leq r$
. Denote the rank function of
![]() $M^t$
by
$M^t$
by
![]() $\rho ^t$
. Then, for every
$\rho ^t$
. Then, for every
![]() $A\subset V$
,
$A\subset V$
,
Proof. Assume first that
![]() $|A|\leq \rho (A)+t$
. Then
$|A|\leq \rho (A)+t$
. Then
![]() $\rho (A) \geq |A|-t$
, and therefore
$\rho (A) \geq |A|-t$
, and therefore
![]() $A\in M^t$
. In particular,
$A\in M^t$
. In particular,
![]() $\rho ^t(A)=|A|$
.
$\rho ^t(A)=|A|$
.
Assume now that
![]() $|A|\geq \rho (A)+t$
. Let
$|A|\geq \rho (A)+t$
. Let
![]() $I\subset A$
such that
$I\subset A$
such that
![]() $|I|=\rho (A)$
and
$|I|=\rho (A)$
and
![]() $I\in M$
. Then, any
$I\in M$
. Then, any
![]() $U\subset A$
of size
$U\subset A$
of size
![]() $\rho (A)+t$
containing I satisfies
$\rho (A)+t$
containing I satisfies
and therefore belongs to
![]() $M^t$
. Thus,
$M^t$
. Thus,
![]() $\rho ^t(A)\geq \rho (A)+t$
. On the other hand, every
$\rho ^t(A)\geq \rho (A)+t$
. On the other hand, every
![]() $U\subset A$
such that
$U\subset A$
such that
![]() $U\in M^t$
satisfies
$U\in M^t$
satisfies
![]() $\rho (U)\geq |U|-t$
, and therefore
$\rho (U)\geq |U|-t$
, and therefore
![]() $|U|\leq \rho (U)+t\leq \rho (A)+t$
. So
$|U|\leq \rho (U)+t\leq \rho (A)+t$
. So
![]() $\rho ^t(A)\leq \rho (A)+t$
.
$\rho ^t(A)\leq \rho (A)+t$
.
Remark 3.3. Given two matroids
![]() $M_1$
and
$M_1$
and
![]() $M_2$
on vertex set V, the matroid union of
$M_2$
on vertex set V, the matroid union of
![]() $M_1$
and
$M_1$
and
![]() $M_2$
is defined as
$M_2$
is defined as
![]() $M_1\vee M_2=\{\sigma \cup \tau :\, \sigma \in M_1,\, \tau \in M_2\}$
. The matroid union theorem (see, e.g., [Reference Oxley15, Sec. 11.3]) states that
$M_1\vee M_2=\{\sigma \cup \tau :\, \sigma \in M_1,\, \tau \in M_2\}$
. The matroid union theorem (see, e.g., [Reference Oxley15, Sec. 11.3]) states that
![]() $M_1\vee M_2$
is a matroid, with rank function
$M_1\vee M_2$
is a matroid, with rank function
![]() $\rho _{12}$
satisfying
$\rho _{12}$
satisfying
for every
![]() $A\subset V$
, where
$A\subset V$
, where
![]() $\rho _1$
and
$\rho _1$
and
![]() $\rho _2$
are the rank functions of
$\rho _2$
are the rank functions of
![]() $M_1$
and
$M_1$
and
![]() $M_2$
, respectively.
$M_2$
, respectively.
Note that
![]() $M^t$
is the matroid union of M and the uniform matroid
$M^t$
is the matroid union of M and the uniform matroid
![]() $\{A\subset V:\, |A|\leq t\}$
. Therefore, Lemma 3.1 and Lemma 3.2 can also be obtained as a consequence of the matroid union theorem.
$\{A\subset V:\, |A|\leq t\}$
. Therefore, Lemma 3.1 and Lemma 3.2 can also be obtained as a consequence of the matroid union theorem.
4 Proof of Theorem 1.6
In this section, we prove Theorem 1.6. Our proof extends the argument for the case
![]() $m=1, k=d+1$
given by Kalai and Meshulam in [Reference Kalai and Meshulam9, Theorem 2.1].
$m=1, k=d+1$
given by Kalai and Meshulam in [Reference Kalai and Meshulam9, Theorem 2.1].
Theorem 1.6. Let
![]() $d\geq 1$
,
$d\geq 1$
,
![]() $r\geq d+1$
,
$r\geq d+1$
,
![]() $1\leq m\leq r$
and
$1\leq m\leq r$
and
![]() $m\leq k\leq \min \{m+d,r\}$
be integers. Let V be a finite set with
$m\leq k\leq \min \{m+d,r\}$
be integers. Let V be a finite set with
![]() $|V|\geq \max \{m+d,r\}$
. Let X be a d-collapsible simplicial complex on vertex set V, and let M be a matroid of rank r on vertex set V with rank function
$|V|\geq \max \{m+d,r\}$
. Let X be a d-collapsible simplicial complex on vertex set V, and let M be a matroid of rank r on vertex set V with rank function
![]() $\rho $
.
$\rho $
.
Assume that, for every
![]() $U=\{u_1,\ldots ,u_d,v_1,\ldots ,v_m\}\subset V$
with
$U=\{u_1,\ldots ,u_d,v_1,\ldots ,v_m\}\subset V$
with
![]() $\rho (U)\geq k$
, there is some
$\rho (U)\geq k$
, there is some
![]() $i\in [m]$
such that
$i\in [m]$
such that
![]() $\{u_1,\ldots ,u_d,v_i\}\in X$
. Then, there is some
$\{u_1,\ldots ,u_d,v_i\}\in X$
. Then, there is some
![]() $\tau \in X$
such that
$\tau \in X$
such that
![]() $\rho (\tau )\geq r+1-m$
and
$\rho (\tau )\geq r+1-m$
and
![]() $\rho (V\setminus \tau )\leq k-1$
.
$\rho (V\setminus \tau )\leq k-1$
.
Proof of Theorem 1.6.
Let
 $$ \begin{align*} \mathcal{R} &=\{\eta\in X:\, |\eta|\geq d+1,\, \rho(\eta)\geq k-m-d+|\eta|\} \\&= \{\eta\in X\cap M^{d+m-k} : \, |\eta|\geq d+1\}. \end{align*} $$
$$ \begin{align*} \mathcal{R} &=\{\eta\in X:\, |\eta|\geq d+1,\, \rho(\eta)\geq k-m-d+|\eta|\} \\&= \{\eta\in X\cap M^{d+m-k} : \, |\eta|\geq d+1\}. \end{align*} $$
By Lemma 2.4, there is some
![]() $U=\{u_1,\ldots ,u_d,v_1,\ldots ,v_{m}\}\subset V$
with
$U=\{u_1,\ldots ,u_d,v_1,\ldots ,v_{m}\}\subset V$
with
![]() $\rho (U)\geq \min \{m+d,r\}\geq k$
. Then, there is some
$\rho (U)\geq \min \{m+d,r\}\geq k$
. Then, there is some
![]() $i\in [m]$
such that
$i\in [m]$
such that
![]() $\sigma _i=\{u_1,\ldots ,u_d,v_i\}\in X$
. Note that
$\sigma _i=\{u_1,\ldots ,u_d,v_i\}\in X$
. Note that
![]() $\sigma _i\subset U\in M^{d+m-k}$
, so
$\sigma _i\subset U\in M^{d+m-k}$
, so
![]() $\sigma _i\in \mathcal {R}$
, and in particular
$\sigma _i\in \mathcal {R}$
, and in particular
![]() $\mathcal {R}\neq \emptyset $
.
$\mathcal {R}\neq \emptyset $
.
By Lemma 2.3, there is a sequence of elementary d-collapses
![]() $X=X_1\to X_2\to \cdots \to X_t$
such that the free faces collapsed at each step are of size exactly d, and
$X=X_1\to X_2\to \cdots \to X_t$
such that the free faces collapsed at each step are of size exactly d, and
![]() $X_t$
satisfies
$X_t$
satisfies
![]() $\dim (X_t)< d-1$
.
$\dim (X_t)< d-1$
.
By definition,
![]() $\mathcal {R}\subset X=X_1$
, and clearly
$\mathcal {R}\subset X=X_1$
, and clearly
![]() $\mathcal {R}\not \subset X_t$
. Let
$\mathcal {R}\not \subset X_t$
. Let
![]() $1\leq n<t$
be the maximal index such that
$1\leq n<t$
be the maximal index such that
![]() $\mathcal {R}\subset X_n$
. Let
$\mathcal {R}\subset X_n$
. Let
![]() $\sigma $
be the free face of size d in the elementary d-collapse
$\sigma $
be the free face of size d in the elementary d-collapse
![]() $X_n\to X_{n+1}$
, and let
$X_n\to X_{n+1}$
, and let
![]() $\tau $
be the unique maximal face of
$\tau $
be the unique maximal face of
![]() $X_n$
containing
$X_n$
containing
![]() $\sigma $
.
$\sigma $
.
Since
![]() $\mathcal {R}\subset X_n$
but
$\mathcal {R}\subset X_n$
but
![]() $\mathcal {R}\not \subset X_{n+1}$
, there is some
$\mathcal {R}\not \subset X_{n+1}$
, there is some
![]() $\sigma \subset \sigma '\subset \tau $
such that
$\sigma \subset \sigma '\subset \tau $
such that
![]() $\sigma '\in M^{d+m-k}$
. In particular, we have
$\sigma '\in M^{d+m-k}$
. In particular, we have
![]() $\sigma \in M^{d+m-k}$
. Let
$\sigma \in M^{d+m-k}$
. Let
Note that, since
![]() $\sigma \in M^{d+m-k}$
, we have
$\sigma \in M^{d+m-k}$
, we have
![]() $\emptyset \in \mathcal {A}$
, and therefore
$\emptyset \in \mathcal {A}$
, and therefore
![]() $\mathcal {A}\neq \emptyset $
. Let
$\mathcal {A}\neq \emptyset $
. Let
![]() $\eta $
be a maximal element of
$\eta $
be a maximal element of
![]() $\mathcal {A}$
.
$\mathcal {A}$
.
First, note that
![]() $|\eta |\leq m-1$
. Otherwise, let
$|\eta |\leq m-1$
. Otherwise, let
![]() $v_1,\ldots ,v_m\in \eta $
, and let
$v_1,\ldots ,v_m\in \eta $
, and let
![]() $U=\sigma \cup \{v_1,\ldots ,v_m\}$
. Then
$U=\sigma \cup \{v_1,\ldots ,v_m\}$
. Then
![]() $U \subset \sigma \cup \eta \in M^{d+m-k}$
, and therefore
$U \subset \sigma \cup \eta \in M^{d+m-k}$
, and therefore
Therefore, there is some
![]() $i\in [m]$
such that
$i\in [m]$
such that
![]() $\sigma _i=\sigma \cup \{v_i\}\in X$
. Since
$\sigma _i=\sigma \cup \{v_i\}\in X$
. Since
![]() $\sigma _i\subset \sigma \cup \eta \in M^{d+m-k}$
, we also have
$\sigma _i\subset \sigma \cup \eta \in M^{d+m-k}$
, we also have
![]() $\sigma _i\in M^{d+m-k}$
. Thus,
$\sigma _i\in M^{d+m-k}$
. Thus,
![]() $\sigma _i\in \mathcal {R}$
, and therefore
$\sigma _i\in \mathcal {R}$
, and therefore
![]() $\sigma _i=\sigma \cup \{v_i\}\in X_n$
, in contradiction to
$\sigma _i=\sigma \cup \{v_i\}\in X_n$
, in contradiction to
![]() $\eta \in \mathcal {A}$
.
$\eta \in \mathcal {A}$
.
Next, note that, for all
![]() $v\in V\setminus \text {span}_M(\sigma \cup \eta )$
, we have
$v\in V\setminus \text {span}_M(\sigma \cup \eta )$
, we have
![]() $\sigma \cup \{v\}\in X_n$
. Otherwise, we would have
$\sigma \cup \{v\}\in X_n$
. Otherwise, we would have
So
![]() $\sigma \cup \eta \cup \{v\}\in M^{d+m-k}$
, and therefore
$\sigma \cup \eta \cup \{v\}\in M^{d+m-k}$
, and therefore
![]() $\eta \cup \{v\}\in \mathcal {A}$
, in contradiction the the maximality of
$\eta \cup \{v\}\in \mathcal {A}$
, in contradiction the the maximality of
![]() $\eta $
. Therefore, since
$\eta $
. Therefore, since
![]() $\sigma $
is contained in the unique maximal face
$\sigma $
is contained in the unique maximal face
![]() $\tau $
of
$\tau $
of
![]() $X_n$
, we obtain
$X_n$
, we obtain
or equivalently,
We divide into two cases: If
![]() $\rho (\sigma \cup \eta )=|\sigma \cup \eta |-(d+m-k)= k-m+|\eta |$
, then
$\rho (\sigma \cup \eta )=|\sigma \cup \eta |-(d+m-k)= k-m+|\eta |$
, then
as wanted.
If
![]() $\rho (\sigma \cup \eta )\geq |\sigma \cup \eta |-(d+m-k)+1$
, then for every
$\rho (\sigma \cup \eta )\geq |\sigma \cup \eta |-(d+m-k)+1$
, then for every
![]() $v\in V\setminus (\sigma \cup \eta )$
, we have
$v\in V\setminus (\sigma \cup \eta )$
, we have
So
![]() $\sigma \cup \eta \cup \{v\}\in M^{d+m-k}$
, and therefore, by the maximality of
$\sigma \cup \eta \cup \{v\}\in M^{d+m-k}$
, and therefore, by the maximality of
![]() $\eta $
in
$\eta $
in
![]() $\mathcal {A}$
, we must have
$\mathcal {A}$
, we must have
![]() $\sigma \cup \{v\}\in X_n$
. Hence, since
$\sigma \cup \{v\}\in X_n$
. Hence, since
![]() $\sigma $
is contained in the unique maximal face
$\sigma $
is contained in the unique maximal face
![]() $\tau $
of
$\tau $
of
![]() $X_n$
, we have
$X_n$
, we have
![]() $V\setminus \eta \subset \tau $
(actually,
$V\setminus \eta \subset \tau $
(actually,
![]() $V\setminus \eta = \tau $
since
$V\setminus \eta = \tau $
since
![]() $\sigma \cup \{u\}\notin X_n$
for all
$\sigma \cup \{u\}\notin X_n$
for all
![]() $u\in \eta $
by the definition of
$u\in \eta $
by the definition of
![]() $\mathcal {A}$
). Thus,
$\mathcal {A}$
). Thus,
Finally, let
![]() $v\in V$
. If
$v\in V$
. If
![]() $v\in \text {span}_M(\sigma \cup \eta )$
, then, since
$v\in \text {span}_M(\sigma \cup \eta )$
, then, since
![]() $\sigma \subset \tau $
, we have
$\sigma \subset \tau $
, we have
![]() $v\in \text {span}_M(\tau \cup \eta )$
. If
$v\in \text {span}_M(\tau \cup \eta )$
. If
![]() $v\notin \text {span}_M(\sigma \cup \eta )$
, then by Equation (4.1),
$v\notin \text {span}_M(\sigma \cup \eta )$
, then by Equation (4.1),
![]() $v\in \tau \subset \text {span}_M(\tau \cup \eta )$
. Thus,
$v\in \tau \subset \text {span}_M(\tau \cup \eta )$
. Thus,
![]() $\text {span}_M(\tau \cup \eta )=V$
, and therefore
$\text {span}_M(\tau \cup \eta )=V$
, and therefore
![]() $\rho (\tau \cup \eta )=\rho (V)=r$
. Hence, by Lemma 2.5, we obtain
$\rho (\tau \cup \eta )=\rho (V)=r$
. Hence, by Lemma 2.5, we obtain
5 Proof of Theorem 1.7
First, we prove the
![]() $m=1$
case of Theorem 1.7:
$m=1$
case of Theorem 1.7:
Theorem 5.1. Let X be a d-Leray simplicial complex on vertex set V. Let M be a matroid on V of rank
![]() $r\geq d+1$
. Denote by
$r\geq d+1$
. Denote by
![]() $\rho $
the rank function of M. Let
$\rho $
the rank function of M. Let
![]() $1\leq k\leq d+1$
.
$1\leq k\leq d+1$
.
Assume that X contains all the sets
![]() $\sigma \subset V$
of size
$\sigma \subset V$
of size
![]() $d+1$
such that
$d+1$
such that
![]() $\rho (\sigma )\geq k$
. Then, there is some
$\rho (\sigma )\geq k$
. Then, there is some
![]() $\tau \in X$
such that
$\tau \in X$
such that
![]() $\rho (V\setminus \tau )\leq k-1$
.
$\rho (V\setminus \tau )\leq k-1$
.
The main tool we will need for the proof is the following result by Kalai and Meshulam (implicit in the proof of [Reference Kalai and Meshulam9, Thm 1.6]; see also [Reference Aharoni, Briggs, Cho and Kim2, Theorem 3] for a similar statement and [Reference Aharoni and Berger1, Theorem 4.5] for an equivalent dual version).
Lemma 5.2 (Kalai–Meshulam [Reference Kalai and Meshulam9]).
Let X be a simplicial complex and M a matroid with rank function
![]() $\rho $
on the same vertex set V. For each
$\rho $
on the same vertex set V. For each
![]() $\sigma \in X$
, let
$\sigma \in X$
, let
If for all
![]() $\sigma \in X$
,
$\sigma \in X$
,
then
![]() $M\not \subset X$
.
$M\not \subset X$
.
We will also need the following well-known simple result.
Lemma 5.3 (Helly’s theorem for d-Leray complexes).
Let X be a d-Leray complex on vertex set V, and let
![]() $U\subset V$
be a set of size at least
$U\subset V$
be a set of size at least
![]() $d+1$
. Assume that every subset of U of size
$d+1$
. Assume that every subset of U of size
![]() $d+1$
is a simplex of X. Then,
$d+1$
is a simplex of X. Then,
![]() $U\in X$
.
$U\in X$
.
Proof. Assume for contradiction that
![]() $U\notin X$
. Let
$U\notin X$
. Let
![]() $S\subset U$
be an inclusion minimal set such that
$S\subset U$
be an inclusion minimal set such that
![]() $S\notin X$
. By the assumption of the lemma, we must have
$S\notin X$
. By the assumption of the lemma, we must have
![]() $|S|\geq d+2$
. But then, by the minimality of S,
$|S|\geq d+2$
. But then, by the minimality of S,
![]() $X[S]$
is just the boundary of a
$X[S]$
is just the boundary of a
![]() $(|S|-1)$
-dimensional simplex, which has nontrivial homology in dimension
$(|S|-1)$
-dimensional simplex, which has nontrivial homology in dimension
![]() $|S|-2 \geq d$
. This is a contradiction to the assumption that X is d-Leray.
$|S|-2 \geq d$
. This is a contradiction to the assumption that X is d-Leray.
Proof of Theorem 5.1.
Assume for contradiction that for all
![]() $\sigma \in X$
,
$\sigma \in X$
,
![]() $\rho (V\setminus \sigma )\geq k$
. In particular, we have
$\rho (V\setminus \sigma )\geq k$
. In particular, we have
![]() $|V\setminus \sigma |\geq k$
for all
$|V\setminus \sigma |\geq k$
for all
![]() $\sigma \in X$
.
$\sigma \in X$
.
Recall that we defined, for
![]() $\sigma \in X$
,
$\sigma \in X$
,
Let
![]() $t=d+1-k$
. In order to apply Lemma 5.2, we will show that
$t=d+1-k$
. In order to apply Lemma 5.2, we will show that
![]() $\rho ^t(V\setminus \sigma )\geq \ell _{\sigma }+1$
for all
$\rho ^t(V\setminus \sigma )\geq \ell _{\sigma }+1$
for all
![]() $\sigma \in X$
.
$\sigma \in X$
.
Let
![]() $\sigma \in X$
. By Lemma 3.2, we have
$\sigma \in X$
. By Lemma 3.2, we have
We divide into two cases:
First, assume
![]() $|V\setminus \sigma |\geq d+1$
. Then, since X is d-Leray, we have, by Lemma 2.2,
$|V\setminus \sigma |\geq d+1$
. Then, since X is d-Leray, we have, by Lemma 2.2,
![]() $\ell _{\sigma }\leq d$
, and therefore
$\ell _{\sigma }\leq d$
, and therefore
Now, assume
![]() $|V\setminus \sigma |\leq d$
. Then, we have
$|V\setminus \sigma |\leq d$
. Then, we have
![]() $\rho ^t(V\setminus \sigma )=|V\setminus \sigma |$
. Since
$\rho ^t(V\setminus \sigma )=|V\setminus \sigma |$
. Since
![]() $|V\setminus \sigma '|\geq k$
for all
$|V\setminus \sigma '|\geq k$
for all
![]() $\sigma '\in X$
, we must have
$\sigma '\in X$
, we must have
![]() $\dim (X)\leq |V|-k-1$
, and therefore
$\dim (X)\leq |V|-k-1$
, and therefore
In particular,
![]() $\ell _{\sigma }\leq |V\setminus \sigma |-k$
. We obtain
$\ell _{\sigma }\leq |V\setminus \sigma |-k$
. We obtain
Hence, by Lemma 5.2, we have
![]() $M^t\not \subset X$
. That is, there is some
$M^t\not \subset X$
. That is, there is some
![]() $\tau \in M^t$
such that
$\tau \in M^t$
such that
![]() $\tau \notin X$
. If
$\tau \notin X$
. If
![]() $|\tau |\geq d+1$
then, by Lemma 5.3, there is some
$|\tau |\geq d+1$
then, by Lemma 5.3, there is some
![]() $\tau '\subset \tau $
of size
$\tau '\subset \tau $
of size
![]() $d+1$
such that
$d+1$
such that
![]() $\tau '\notin X$
. If
$\tau '\notin X$
. If
![]() $|\tau |<d+1$
, then, since
$|\tau |<d+1$
, then, since
![]() $M^t$
is a matroid of rank
$M^t$
is a matroid of rank
![]() $r\geq d+1>|\tau |$
, there is some
$r\geq d+1>|\tau |$
, there is some
![]() $\tau '\supset \tau $
of size
$\tau '\supset \tau $
of size
![]() $d+1$
such that
$d+1$
such that
![]() $\tau '\in M^t$
, and, since
$\tau '\in M^t$
, and, since
![]() $\tau \notin X$
, we also have
$\tau \notin X$
, we also have
![]() $\tau '\notin X$
.
$\tau '\notin X$
.
In both cases, since
![]() $\tau '\in M^t$
, we have
$\tau '\in M^t$
, we have
but this is a contradiction to the assumption of the theorem.
For the proof of Theorem 1.7, we will need the following Lemma about d-Leray complexes.
Lemma 5.4. Let X be a d-Leray complex on vertex set V, and let
![]() $A\subset d+1$
such that
$A\subset d+1$
such that
![]() $A\notin X$
. Let
$A\notin X$
. Let
Assume that
![]() $U\neq \emptyset $
. Then, for every
$U\neq \emptyset $
. Then, for every
![]() $a\in A$
,
$a\in A$
,
![]() $U\cup A\setminus \{a\}\in X$
.
$U\cup A\setminus \{a\}\in X$
.
Proof. Given a set
![]() $B\subset V$
and
$B\subset V$
and
![]() $i\geq 0$
, we denote by
$i\geq 0$
, we denote by
![]() $\binom {B}{i}$
the family of all subsets of B of size i, and we denote by
$\binom {B}{i}$
the family of all subsets of B of size i, and we denote by
![]() $\partial 2^B$
the boundary of the simplex on vertex set B, that is, the simplicial complex consisting of all proper subsets of B.
$\partial 2^B$
the boundary of the simplex on vertex set B, that is, the simplicial complex consisting of all proper subsets of B.
First, note that, since
![]() $U\neq \emptyset $
, we must have
$U\neq \emptyset $
, we must have
![]() $\sigma \in X$
for every
$\sigma \in X$
for every
![]() $\sigma \subsetneq A$
. That is,
$\sigma \subsetneq A$
. That is,
![]() $\partial 2^A\subset X$
. We will show that, for every
$\partial 2^A\subset X$
. We will show that, for every
![]() $1\leq i\leq |U|$
and
$1\leq i\leq |U|$
and
![]() $W \in \binom {U}{i}$
,
$W \in \binom {U}{i}$
,
![]() $X[A\cup W] = \partial 2^A\ast 2^{W}$
. We argue by induction on i. The base case
$X[A\cup W] = \partial 2^A\ast 2^{W}$
. We argue by induction on i. The base case
![]() $i=1$
is obvious by the definition of U. Suppose, for some
$i=1$
is obvious by the definition of U. Suppose, for some
![]() $1\leq i<|U|$
, that
$1\leq i<|U|$
, that
![]() $X[A\cup T] =\partial 2^A\ast 2^{T}$
for every
$X[A\cup T] =\partial 2^A\ast 2^{T}$
for every
![]() $T \in \binom {U}{i}$
. Let
$T \in \binom {U}{i}$
. Let
![]() $W = \{u_1,u_2,\ldots ,u_{i+1}\} \subset U$
.
$W = \{u_1,u_2,\ldots ,u_{i+1}\} \subset U$
.
Consider
Note that, by Lemma 2.2,
![]() $\tilde {H}_j(L) = 0$
for every
$\tilde {H}_j(L) = 0$
for every
![]() $j \geq d$
. Furthermore, by the induction hypothesis, we have
$j \geq d$
. Furthermore, by the induction hypothesis, we have
![]() $X[A\cup (W\setminus \{u_{i}\})]=\partial 2^A \ast 2^{W\setminus \{u_{i}\}}$
, and therefore
$X[A\cup (W\setminus \{u_{i}\})]=\partial 2^A \ast 2^{W\setminus \{u_{i}\}}$
, and therefore
![]() $L \setminus u_{i} = \partial 2^A\ast 2^{\{u_{i+1}\}}$
. In particular,
$L \setminus u_{i} = \partial 2^A\ast 2^{\{u_{i+1}\}}$
. In particular,
![]() $L\setminus u_i$
contractible, and thus
$L\setminus u_i$
contractible, and thus
![]() $\tilde {H}_j(L\setminus u_i)=0$
for all
$\tilde {H}_j(L\setminus u_i)=0$
for all
![]() $j\geq 0$
. By Theorem 2.1, there exists a long exact sequence
$j\geq 0$
. By Theorem 2.1, there exists a long exact sequence
We obtain that
Since
![]() $\partial 2^A \subset \operatorname {\mathrm {lk}}(L, u_i)=\operatorname {\mathrm {lk}}(X[A\cup W], \{u_1,u_2,\ldots ,u_{i}\})$
, there must be a d-dimensional chain in
$\partial 2^A \subset \operatorname {\mathrm {lk}}(L, u_i)=\operatorname {\mathrm {lk}}(X[A\cup W], \{u_1,u_2,\ldots ,u_{i}\})$
, there must be a d-dimensional chain in
![]() $\operatorname {\mathrm {lk}}(L, u_i)$
whose boundary equals to
$\operatorname {\mathrm {lk}}(L, u_i)$
whose boundary equals to
![]() $\partial 2^A$
. For each
$\partial 2^A$
. For each
![]() $(d-1)$
-dimensional simplex
$(d-1)$
-dimensional simplex
![]() $\sigma $
in
$\sigma $
in
![]() $\partial 2^A$
, the only possible d-dimensional simplex of
$\partial 2^A$
, the only possible d-dimensional simplex of
![]() $\operatorname {\mathrm {lk}}(L, u_i)$
containing
$\operatorname {\mathrm {lk}}(L, u_i)$
containing
![]() $\sigma $
is
$\sigma $
is
![]() $\sigma \cup \{u_{i+1}\}$
. This shows
$\sigma \cup \{u_{i+1}\}$
. This shows
![]() $\partial 2^A \ast 2^{\{u_{i+1}\}}\subset \operatorname {\mathrm {lk}}(L,u_i)$
. Since
$\partial 2^A \ast 2^{\{u_{i+1}\}}\subset \operatorname {\mathrm {lk}}(L,u_i)$
. Since
![]() $A\notin \operatorname {\mathrm {lk}}(L,u_i)$
, we must actually have
$A\notin \operatorname {\mathrm {lk}}(L,u_i)$
, we must actually have
![]() $\operatorname {\mathrm {lk}}(L, u_i) = \partial 2^A\ast 2^{\{u_{i+1}\}} $
, and hence we have
$\operatorname {\mathrm {lk}}(L, u_i) = \partial 2^A\ast 2^{\{u_{i+1}\}} $
, and hence we have
![]() $X[A\cup W] = \partial 2^A \ast 2^W$
.
$X[A\cup W] = \partial 2^A \ast 2^W$
.
Finally, letting
![]() $i=|U|$
, we obtain that
$i=|U|$
, we obtain that
![]() $\partial 2^A\ast 2^U \subset X$
, as desired.
$\partial 2^A\ast 2^U \subset X$
, as desired.
Theorem 1.7. Let
![]() $d\geq 1$
,
$d\geq 1$
,
![]() $r\geq d+1$
,
$r\geq d+1$
,
![]() $1\leq m\leq r$
and
$1\leq m\leq r$
and
![]() $m\leq k\leq \min \{m+d,r\}$
be integers. Let V be a finite set with
$m\leq k\leq \min \{m+d,r\}$
be integers. Let V be a finite set with
![]() $|V|\geq \max \{m+d,r\}$
. Let X be a d-Leray simplicial complex on vertex set V, and let M be a matroid of rank r on vertex set V with rank function
$|V|\geq \max \{m+d,r\}$
. Let X be a d-Leray simplicial complex on vertex set V, and let M be a matroid of rank r on vertex set V with rank function
![]() $\rho $
.
$\rho $
.
Assume that for every
![]() $U=\{u_1,\ldots ,u_{d+1},v_1,\ldots ,v_{m-1}\}\subset V$
with
$U=\{u_1,\ldots ,u_{d+1},v_1,\ldots ,v_{m-1}\}\subset V$
with
![]() $\rho (U)\geq k$
, either
$\rho (U)\geq k$
, either
![]() $\{u_1,\ldots ,u_{d+1}\}\in X$
or there exists
$\{u_1,\ldots ,u_{d+1}\}\in X$
or there exists
![]() $j\in [m-1]$
such that
$j\in [m-1]$
such that
![]() $\sigma \cup \{v_j\}\in X$
for every
$\sigma \cup \{v_j\}\in X$
for every
![]() $\sigma \subsetneq \{u_1,\ldots ,u_{d+1}\}$
. Then, there is some
$\sigma \subsetneq \{u_1,\ldots ,u_{d+1}\}$
. Then, there is some
![]() $\tau \in X$
such that
$\tau \in X$
such that
![]() $\rho (V\setminus \tau ) \leq k-1$
.
$\rho (V\setminus \tau ) \leq k-1$
.
Proof. We argue by induction on m. For
![]() $m=1$
the claim holds by Theorem 5.1. Let
$m=1$
the claim holds by Theorem 5.1. Let
![]() $m>1$
, and assume that the claim holds for
$m>1$
, and assume that the claim holds for
![]() $m-1$
.
$m-1$
.
If for all
![]() $U=\{u_1,\ldots ,u_{d+1},v_1,\ldots ,v_{m-2}\}\subset V$
with
$U=\{u_1,\ldots ,u_{d+1},v_1,\ldots ,v_{m-2}\}\subset V$
with
![]() $\rho (U)\geq k-1$
, either
$\rho (U)\geq k-1$
, either
![]() $\{u_1,\ldots ,u_{d+1}\}\in X$
or there is some
$\{u_1,\ldots ,u_{d+1}\}\in X$
or there is some
![]() $1\leq j\leq m-2$
such that
$1\leq j\leq m-2$
such that
![]() $\sigma \cup \{v_j\}\in X$
for all
$\sigma \cup \{v_j\}\in X$
for all
![]() $\sigma \subsetneq \{u_1,\ldots ,u_{d+1}\}$
, then by the induction hypothesis there is some
$\sigma \subsetneq \{u_1,\ldots ,u_{d+1}\}$
, then by the induction hypothesis there is some
![]() $\tau \in X$
such that
$\tau \in X$
such that
![]() $\rho (V\setminus \tau )\leq k-2\leq k-1$
, as wanted.
$\rho (V\setminus \tau )\leq k-2\leq k-1$
, as wanted.
Otherwise, there exists
![]() $U=\{u_1,\ldots ,u_{d+1},v_1,\ldots ,v_{m-2}\}\subset V$
with
$U=\{u_1,\ldots ,u_{d+1},v_1,\ldots ,v_{m-2}\}\subset V$
with
![]() $\rho (U)\geq k-1$
such that
$\rho (U)\geq k-1$
such that
![]() $A=\{u_1,\ldots ,u_{d+1}\}\notin X$
and for every
$A=\{u_1,\ldots ,u_{d+1}\}\notin X$
and for every
![]() $1\leq j\leq m-2$
there is some
$1\leq j\leq m-2$
there is some
![]() $\sigma _j\subsetneq A$
such that
$\sigma _j\subsetneq A$
such that
![]() $\sigma _j\cup \{v_j\}\notin X$
. We divide into two cases: First, assume that
$\sigma _j\cup \{v_j\}\notin X$
. We divide into two cases: First, assume that
![]() $\rho (U)=k-1$
. Then, for any
$\rho (U)=k-1$
. Then, for any
![]() $v\in V\setminus \text {span}_M(U)$
, we have
$v\in V\setminus \text {span}_M(U)$
, we have
![]() $\rho (\{u_1,\ldots ,u_{d+1},v_1,\ldots ,v_{m-2},v\})\geq k$
, and therefore by the assumption of the theorem we must have
$\rho (\{u_1,\ldots ,u_{d+1},v_1,\ldots ,v_{m-2},v\})\geq k$
, and therefore by the assumption of the theorem we must have
![]() $\sigma \cup \{v\}\in X$
for all
$\sigma \cup \{v\}\in X$
for all
![]() $\sigma \subsetneq A$
. Note that, since
$\sigma \subsetneq A$
. Note that, since
![]() $\rho (V)=r \geq k>\rho (U)$
, we must have
$\rho (V)=r \geq k>\rho (U)$
, we must have
![]() $V\setminus \text {span}_M(U)\neq \emptyset $
. Hence, by Lemma 5.4, we have
$V\setminus \text {span}_M(U)\neq \emptyset $
. Hence, by Lemma 5.4, we have
![]() $\tau =V\setminus \text {span}_M(U)\in X$
. Note that
$\tau =V\setminus \text {span}_M(U)\in X$
. Note that
![]() $\rho (V\setminus \tau )=\rho (U)= k-1$
, as desired.
$\rho (V\setminus \tau )=\rho (U)= k-1$
, as desired.
Next, assume that
![]() $\rho (U)\geq k$
. Then, for any
$\rho (U)\geq k$
. Then, for any
![]() $v\in V\setminus U$
, we have
$v\in V\setminus U$
, we have
![]() $\rho (\{u_1,\ldots ,u_{d+1},v_1,\ldots ,v_{m-2},v\})\geq \rho (U)\geq k$
, and therefore by the assumption of the theorem, we must have
$\rho (\{u_1,\ldots ,u_{d+1},v_1,\ldots ,v_{m-2},v\})\geq \rho (U)\geq k$
, and therefore by the assumption of the theorem, we must have
![]() $\sigma \cup \{v\}\in X$
for every
$\sigma \cup \{v\}\in X$
for every
![]() $\sigma \subsetneq A$
. Note that, since
$\sigma \subsetneq A$
. Note that, since
![]() $|V|\geq d+m \geq |U|+1$
, we must have
$|V|\geq d+m \geq |U|+1$
, we must have
![]() $V\setminus U\neq \emptyset $
. So, by Lemma 5.4, we have
$V\setminus U\neq \emptyset $
. So, by Lemma 5.4, we have
![]() $\tau =(V\setminus U)\cup \{u_1,\ldots ,u_d\}\in X$
. Since
$\tau =(V\setminus U)\cup \{u_1,\ldots ,u_d\}\in X$
. Since
![]() $\rho (V\setminus \tau )=\rho (\{u_{d+1},v_1,\ldots ,v_{m-2})\leq m-1\leq k-1$
, we are done.
$\rho (V\setminus \tau )=\rho (\{u_{d+1},v_1,\ldots ,v_{m-2})\leq m-1\leq k-1$
, we are done.
6 Geometric applications
6.1 Colorful Helly and Carathéodory theorems
In this section, we present a proof of Theorem 1.9 and show how to derive from it an analogous extension of Bárány’s colorful Carathéodory theorem [Reference Bárány4]. The arguments in this section are standard and well known (see, e.g., [Reference Kalai and Meshulam9, Reference Bárány4]), but we include detailed proofs for completeness.
Theorem 1.9. Let
![]() $d\geq 1$
,
$d\geq 1$
,
![]() $r\geq d+1$
,
$r\geq d+1$
,
![]() $1\leq m\leq r$
and
$1\leq m\leq r$
and
![]() $m\leq k\leq \min \{m+d,r\}$
. Let
$m\leq k\leq \min \{m+d,r\}$
. Let
![]() $\mathcal {C}$
be a finite family of convex sets in
$\mathcal {C}$
be a finite family of convex sets in
![]() ${\mathbb R}^d$
, colored with r different colors, of size
${\mathbb R}^d$
, colored with r different colors, of size
![]() $|\mathcal {C}|\geq \max \{m+d,r\}$
. Assume that, for every family
$|\mathcal {C}|\geq \max \{m+d,r\}$
. Assume that, for every family
![]() $\{A_1,\ldots ,A_d,B_1,\ldots ,B_m\}\subset \mathcal {C}$
, colored with at least k different colors, at least one of the subfamilies of the form
$\{A_1,\ldots ,A_d,B_1,\ldots ,B_m\}\subset \mathcal {C}$
, colored with at least k different colors, at least one of the subfamilies of the form
![]() $\{A_1,\ldots ,A_d,B_i\}$
, for
$\{A_1,\ldots ,A_d,B_i\}$
, for
![]() $i\in [m]$
, is intersecting. Then, there are
$i\in [m]$
, is intersecting. Then, there are
![]() $r-k+1$
color classes whose union is intersecting.
$r-k+1$
color classes whose union is intersecting.
Proof. Let X be the nerve of the family
![]() $\mathcal {C}$
. By Wegner’s theorem [Reference Wegner24], X is d-collapsible. Let
$\mathcal {C}$
. By Wegner’s theorem [Reference Wegner24], X is d-collapsible. Let
![]() $\mathcal {C}_1,\ldots ,\mathcal {C}_r$
be the color classes of
$\mathcal {C}_1,\ldots ,\mathcal {C}_r$
be the color classes of
![]() $\mathcal {C}$
. Let M be the partition matroid on vertex set
$\mathcal {C}$
. Let M be the partition matroid on vertex set
![]() $\mathcal {C}$
, corresponding to the partition
$\mathcal {C}$
, corresponding to the partition
![]() $\mathcal {C}=\mathcal {C}_1\cup \cdots \cup \mathcal {C}_r$
. That is, the independent sets of M are exactly the colorful subfamilies of
$\mathcal {C}=\mathcal {C}_1\cup \cdots \cup \mathcal {C}_r$
. That is, the independent sets of M are exactly the colorful subfamilies of
![]() $\mathcal {C}$
, and the rank function
$\mathcal {C}$
, and the rank function
![]() $\rho $
satisfies
$\rho $
satisfies
for all
![]() $\mathcal {C}'\subset \mathcal {C}$
. That is,
$\mathcal {C}'\subset \mathcal {C}$
. That is,
![]() $\rho (\mathcal {C}')$
is the number of different colors appearing in
$\rho (\mathcal {C}')$
is the number of different colors appearing in
![]() $\mathcal {C}'$
.
$\mathcal {C}'$
.
Let
![]() $U=\{A_1,\ldots ,A_d,B_1,\ldots ,B_m\}\subset V$
be a subfamily colored with at least k different colors (or equivalently, satisfying
$U=\{A_1,\ldots ,A_d,B_1,\ldots ,B_m\}\subset V$
be a subfamily colored with at least k different colors (or equivalently, satisfying
![]() $\rho (U)\geq k$
). Then, there is some
$\rho (U)\geq k$
). Then, there is some
![]() $i\in [m]$
such that
$i\in [m]$
such that
![]() $\{A_1,\ldots ,A_d,B_i\}$
is intersecting. In other words,
$\{A_1,\ldots ,A_d,B_i\}$
is intersecting. In other words,
![]() $\{A_1,\ldots ,A_d,B_i\}\in X$
. Therefore, by Theorem 1.6, there is some
$\{A_1,\ldots ,A_d,B_i\}\in X$
. Therefore, by Theorem 1.6, there is some
![]() $\tau \in X$
such that
$\tau \in X$
such that
![]() $\rho (V\setminus \tau )\leq k-1$
. That is,
$\rho (V\setminus \tau )\leq k-1$
. That is,
![]() $\tau \subset \mathcal {C}$
is an intersecting subfamily, whose complement intersects at most
$\tau \subset \mathcal {C}$
is an intersecting subfamily, whose complement intersects at most
![]() $k-1$
color classes. This means that
$k-1$
color classes. This means that
![]() $\tau $
contains at least
$\tau $
contains at least
![]() $r-k+1$
entire color classes, as wanted.
$r-k+1$
entire color classes, as wanted.
Theorem 6.1. Let
![]() $d\geq 1$
,
$d\geq 1$
,
![]() $r\geq d+1$
,
$r\geq d+1$
,
![]() $1\leq m\leq r$
and
$1\leq m\leq r$
and
![]() $m\leq k\leq \min \{m+d,r\}$
. Let P be a finite family of points in
$m\leq k\leq \min \{m+d,r\}$
. Let P be a finite family of points in
![]() ${\mathbb R}^d$
colored with r colors of size
${\mathbb R}^d$
colored with r colors of size
![]() $|P|\geq \max \{m+d,r\}$
.
$|P|\geq \max \{m+d,r\}$
.
Assume that the convex hull of the union of every
![]() $r-k+1$
color classes contains the origin. Then, there is some
$r-k+1$
color classes contains the origin. Then, there is some
![]() $\{u_1,\ldots ,u_d,v_1,\ldots ,v_m\}\subset P$
, colored with at least k different colors, such that
$\{u_1,\ldots ,u_d,v_1,\ldots ,v_m\}\subset P$
, colored with at least k different colors, such that
![]() $0\in \operatorname {\mathrm {\text {conv}}}(\{u_1,\ldots ,u_d,v_i\})$
for all
$0\in \operatorname {\mathrm {\text {conv}}}(\{u_1,\ldots ,u_d,v_i\})$
for all
![]() $i\in [m]$
.
$i\in [m]$
.
Proof. For each
![]() $p\in P$
, let
$p\in P$
, let
![]() $H_p\subset {\mathbb R}^d$
be defined as
$H_p\subset {\mathbb R}^d$
be defined as
Note that, for
![]() $p\neq 0$
,
$p\neq 0$
,
![]() $H_p$
is an open half-space, and for
$H_p$
is an open half-space, and for
![]() $p=0$
,
$p=0$
,
![]() $H_p=\emptyset $
. In particular,
$H_p=\emptyset $
. In particular,
![]() $H_p$
is convex for all
$H_p$
is convex for all
![]() $p\in P$
.
$p\in P$
.
It is a well-known fact that for any
![]() $P'\subset P$
,
$P'\subset P$
,
![]() $0\in \operatorname {\mathrm {\text {conv}}}(P')$
if and only if
$0\in \operatorname {\mathrm {\text {conv}}}(P')$
if and only if
![]() $\cap _{p\in P'} H_p=\emptyset $
. Indeed, assume first that
$\cap _{p\in P'} H_p=\emptyset $
. Indeed, assume first that
![]() $\cap _{p\in P'} H_p\neq \emptyset $
. That is, there is some
$\cap _{p\in P'} H_p\neq \emptyset $
. That is, there is some
![]() $x\in {\mathbb R}^d$
such that
$x\in {\mathbb R}^d$
such that
![]() $x\cdot p>0$
for all
$x\cdot p>0$
for all
![]() $p\in P'$
. Let
$p\in P'$
. Let
![]() $\{t_p\}_{p\in P'}$
be nonnegative real numbers such that
$\{t_p\}_{p\in P'}$
be nonnegative real numbers such that
![]() $\sum _{p\in P'} t_p=1$
. Then, there is some
$\sum _{p\in P'} t_p=1$
. Then, there is some
![]() $p_0\in P'$
such that
$p_0\in P'$
such that
![]() $t_{p_0}>0$
. Thus, we obtain
$t_{p_0}>0$
. Thus, we obtain
 $$\begin{align*}\left(\sum_{p\in P'} t_p p\right) \cdot x = \sum_{p\in P'} t_p (p\cdot x)\geq t_{p_0}(p_0\cdot x)>0. \end{align*}$$
$$\begin{align*}\left(\sum_{p\in P'} t_p p\right) \cdot x = \sum_{p\in P'} t_p (p\cdot x)\geq t_{p_0}(p_0\cdot x)>0. \end{align*}$$
Therefore,
![]() $0\notin \operatorname {\mathrm {\text {conv}}}(P')$
. In the other direction, assume that
$0\notin \operatorname {\mathrm {\text {conv}}}(P')$
. In the other direction, assume that
![]() $0\notin \operatorname {\mathrm {\text {conv}}}(P')$
. Then, there is some hyperplane separating
$0\notin \operatorname {\mathrm {\text {conv}}}(P')$
. Then, there is some hyperplane separating
![]() $0$
from
$0$
from
![]() $ \operatorname {\mathrm {\text {conv}}}(P')$
. In other words, there exists
$ \operatorname {\mathrm {\text {conv}}}(P')$
. In other words, there exists
![]() $x\in {\mathbb R}^d$
such that
$x\in {\mathbb R}^d$
such that
![]() $x\cdot y>0$
for all
$x\cdot y>0$
for all
![]() $y\in \operatorname {\mathrm {\text {conv}}}(P')$
. In particular,
$y\in \operatorname {\mathrm {\text {conv}}}(P')$
. In particular,
![]() $x\in H_p$
for all
$x\in H_p$
for all
![]() $p\in P'$
. Therefore,
$p\in P'$
. Therefore,
![]() $\cap _{p\in P'} H_p\neq \emptyset $
.
$\cap _{p\in P'} H_p\neq \emptyset $
.
We color the family
![]() $\mathcal {H}=\{H_p\}_{p\in P}$
in r colors, each set
$\mathcal {H}=\{H_p\}_{p\in P}$
in r colors, each set
![]() $H_p$
colored with the color of p. Assume for contradiction that for all
$H_p$
colored with the color of p. Assume for contradiction that for all
![]() $\{u_1,\ldots ,u_d,v_1,\ldots ,v_m\}\subset P$
, colored with at least k colors,
$\{u_1,\ldots ,u_d,v_1,\ldots ,v_m\}\subset P$
, colored with at least k colors,
![]() $0\notin \operatorname {\mathrm {\text {conv}}}(\{u_1,\ldots ,u_d,v_i\})$
for some
$0\notin \operatorname {\mathrm {\text {conv}}}(\{u_1,\ldots ,u_d,v_i\})$
for some
![]() $i\in [m]$
. Equivalently, for all
$i\in [m]$
. Equivalently, for all
![]() $\{H_{u_1},\ldots ,H_{u_d},H_{v_1},\ldots ,H_{v_m}\}\subset \mathcal {H}$
, colored with at least k colors,
$\{H_{u_1},\ldots ,H_{u_d},H_{v_1},\ldots ,H_{v_m}\}\subset \mathcal {H}$
, colored with at least k colors,
![]() $\{ H_{u_1},\ldots ,H_{u_d},H_{v_i}\}$
is intersecting for some
$\{ H_{u_1},\ldots ,H_{u_d},H_{v_i}\}$
is intersecting for some
![]() $i\in [m]$
.
$i\in [m]$
.
By Theorem 1.9, there are
![]() $r-k+1$
color classes in
$r-k+1$
color classes in
![]() $\mathcal {H}$
whose union is intersecting. Equivalently, there are
$\mathcal {H}$
whose union is intersecting. Equivalently, there are
![]() $r-k+1$
color classes in P that do not contain the origin in the convex hull of their union. But this is a contradiction to the assumption of the theorem.
$r-k+1$
color classes in P that do not contain the origin in the convex hull of their union. But this is a contradiction to the assumption of the theorem.
For the next section, we will need the special case
![]() $r=k=d+m$
of Theorem 6.1:
$r=k=d+m$
of Theorem 6.1:
Theorem 6.2. Let
![]() $d\geq 1$
and
$d\geq 1$
and
![]() $m\geq 1$
. Let P be a finite family of points in
$m\geq 1$
. Let P be a finite family of points in
![]() ${\mathbb R}^d$
colored with
${\mathbb R}^d$
colored with
![]() $d+m$
colors. Assume that the convex hull of every color class contains the origin. Then, there is some colorful set
$d+m$
colors. Assume that the convex hull of every color class contains the origin. Then, there is some colorful set
![]() $\{u_1,\ldots ,u_d,v_1,\ldots ,v_m\}\subset P$
such that
$\{u_1,\ldots ,u_d,v_1,\ldots ,v_m\}\subset P$
such that
![]() $0\in \operatorname {\mathrm {\text {conv}}}(\{u_1,\ldots ,u_d,v_i\})$
for all
$0\in \operatorname {\mathrm {\text {conv}}}(\{u_1,\ldots ,u_d,v_i\})$
for all
![]() $i\in [m]$
.
$i\in [m]$
.
6.2 Tverberg centers for large point sets
In this section, we prove Theorem 1.10. Theorem 1.10 follows from Theorem 6.2 by a straightforward adaptation of Sarkaria’s proof of Tverberg’s theorem via the colorful Carathéodory theorem [Reference Sarkaria19]. For completeness, we write down the argument, closely following the exposition in [Reference Arocha, Bárány, Bracho, Fabila and Montejano3] (which in turn is based on Bárány and Onn’s variant of Sarkaria’s proof given in [Reference Bárány and Onn5]).
First, we will need the following Lemma:
Lemma 6.3 (Sarkaria (see, e.g., [Reference Arocha, Bárány, Bracho, Fabila and Montejano3, Lemma 2])).
Let
![]() $P_1,\ldots ,P_r$
be finite sets of points in
$P_1,\ldots ,P_r$
be finite sets of points in
![]() ${\mathbb R}^d$
. Let
${\mathbb R}^d$
. Let
![]() $v_1,\ldots ,v_r\in {\mathbb R}^{r-1}$
be the vertices of the standard
$v_1,\ldots ,v_r\in {\mathbb R}^{r-1}$
be the vertices of the standard
![]() $(r-1)$
-dimensional simplex. Define
$(r-1)$
-dimensional simplex. Define
 $$\begin{align*}\bar{P}= \left\{ \begin{pmatrix} x\\1 \end{pmatrix}\otimes v_j :\, j\in[r],\, x\in P_j\right\}\subset {\mathbb R}^{(r-1)(d+1)}, \end{align*}$$
$$\begin{align*}\bar{P}= \left\{ \begin{pmatrix} x\\1 \end{pmatrix}\otimes v_j :\, j\in[r],\, x\in P_j\right\}\subset {\mathbb R}^{(r-1)(d+1)}, \end{align*}$$
where
![]() $\otimes $
denotes the Kronecker product. Then
$\otimes $
denotes the Kronecker product. Then
![]() $\cap _{j=1}^r \operatorname {\mathrm {\text {conv}}}(P_j)=\emptyset $
if and only if
$\cap _{j=1}^r \operatorname {\mathrm {\text {conv}}}(P_j)=\emptyset $
if and only if
![]() $0\notin \operatorname {\mathrm {\text {conv}}}(\bar {P})$
.
$0\notin \operatorname {\mathrm {\text {conv}}}(\bar {P})$
.
Theorem 1.10. Let
![]() $d\geq 1$
,
$d\geq 1$
,
![]() $r\geq 2$
, and let
$r\geq 2$
, and let
![]() $n=(r-1)(d+1)$
. Let
$n=(r-1)(d+1)$
. Let
![]() $A\subset {\mathbb R}^d$
be a finite set of points of size larger than n. Then, there exists a partition
$A\subset {\mathbb R}^d$
be a finite set of points of size larger than n. Then, there exists a partition
![]() $A_1,\ldots ,A_r$
of A that has a Tverberg center of size n.
$A_1,\ldots ,A_r$
of A that has a Tverberg center of size n.
Proof. Let
![]() $n=(r-1)(d+1)$
and
$n=(r-1)(d+1)$
and
![]() $m=|A|-n$
. Write
$m=|A|-n$
. Write
![]() $A=\{x_1,\ldots ,x_{n+m}\}$
. For
$A=\{x_1,\ldots ,x_{n+m}\}$
. For
![]() $1\leq i\leq m+n$
and
$1\leq i\leq m+n$
and
![]() $1\leq j\leq r$
, let
$1\leq j\leq r$
, let
![]() $x_i^j$
be a copy of the point
$x_i^j$
be a copy of the point
![]() $x_i$
. For
$x_i$
. For
![]() $1\leq j\leq r$
, let
$1\leq j\leq r$
, let
![]() $P_j=\{x_1^j,\ldots ,x_{n+m}^j\}$
, and let
$P_j=\{x_1^j,\ldots ,x_{n+m}^j\}$
, and let
![]() $P=P_1\cup \cdots \cup P_r$
. Let
$P=P_1\cup \cdots \cup P_r$
. Let
![]() $v_1,\ldots ,v_r\in {\mathbb R}^{r-1}$
be the vertices of the standard simplex, and define for each
$v_1,\ldots ,v_r\in {\mathbb R}^{r-1}$
be the vertices of the standard simplex, and define for each
![]() $1\leq i\leq n+m$
and
$1\leq i\leq n+m$
and
![]() $1\leq j\leq r$
,
$1\leq j\leq r$
,
 $$\begin{align*}\bar{x}_i^j = \begin{pmatrix} x_i^j\\1 \end{pmatrix}\otimes v_j\in {\mathbb R}^n. \end{align*}$$
$$\begin{align*}\bar{x}_i^j = \begin{pmatrix} x_i^j\\1 \end{pmatrix}\otimes v_j\in {\mathbb R}^n. \end{align*}$$
Let
![]() $\bar {P}=\{\bar {x}_i^j :\, 1\leq i\leq n+m, 1\leq j\leq r\}$
. We color the points in P with
$\bar {P}=\{\bar {x}_i^j :\, 1\leq i\leq n+m, 1\leq j\leq r\}$
. We color the points in P with
![]() $|A|=n+m$
colors, where, for
$|A|=n+m$
colors, where, for
![]() $1\leq i\leq n+m$
and
$1\leq i\leq n+m$
and
![]() $1\leq j\leq r$
,
$1\leq j\leq r$
,
![]() $x_i^j$
is colored with color i. Similarly, we color
$x_i^j$
is colored with color i. Similarly, we color
![]() $\bar {P}$
with
$\bar {P}$
with
![]() $n+m$
colors, where, for
$n+m$
colors, where, for
![]() $1\leq i\leq n+m$
and
$1\leq i\leq n+m$
and
![]() $1\leq j\leq r$
,
$1\leq j\leq r$
,
![]() $\bar {x}_i^j$
is colored with color i.
$\bar {x}_i^j$
is colored with color i.
Note that for each color class
![]() $C_i=\{x_i^j :\, 1\leq j\leq r\}$
,
$C_i=\{x_i^j :\, 1\leq j\leq r\}$
,
![]() $1\leq i\leq n+m$
, we have
$1\leq i\leq n+m$
, we have
![]() $\cap _{j=1}^r \operatorname {\mathrm {\text {conv}}}(C_i\cap P_j)=\cap _{j=1}^r\operatorname {\mathrm {\text {conv}}}(\{x_i^j\})= \{x_i\}\neq \emptyset $
. So, by Lemma 6.3, we have
$\cap _{j=1}^r \operatorname {\mathrm {\text {conv}}}(C_i\cap P_j)=\cap _{j=1}^r\operatorname {\mathrm {\text {conv}}}(\{x_i^j\})= \{x_i\}\neq \emptyset $
. So, by Lemma 6.3, we have
for all
![]() $1\leq i\leq n+m$
. That is, the convex hull of each of the color classes of
$1\leq i\leq n+m$
. That is, the convex hull of each of the color classes of
![]() $\bar {P}$
contains the origin. Therefore, by Theorem 6.2, there is a colorful set
$\bar {P}$
contains the origin. Therefore, by Theorem 6.2, there is a colorful set
![]() $U=\{\bar {x}_{a_1}^{b_1},\ldots ,\bar {x}_{a_{n+m}}^{b_{n+m}}\}\subset \bar {P}$
such that
$U=\{\bar {x}_{a_1}^{b_1},\ldots ,\bar {x}_{a_{n+m}}^{b_{n+m}}\}\subset \bar {P}$
such that
for all
![]() $1\leq i\leq m$
. Since U is colorful, the index set
$1\leq i\leq m$
. Since U is colorful, the index set
![]() $\{a_1,\ldots ,a_{n+m}\}$
is a permutation of
$\{a_1,\ldots ,a_{n+m}\}$
is a permutation of
![]() $[n+m]$
. Therefore, we can define a partition
$[n+m]$
. Therefore, we can define a partition
![]() $A=A_1\cup \cdots \cup A_r$
by
$A=A_1\cup \cdots \cup A_r$
by
for
![]() $1\leq j\leq r$
. Let
$1\leq j\leq r$
. Let
![]() $B=\{ x_{a_1},\ldots ,x_{a_n}\}\subset A$
. By Lemma 6.3, Equation (6.1) implies that for all
$B=\{ x_{a_1},\ldots ,x_{a_n}\}\subset A$
. By Lemma 6.3, Equation (6.1) implies that for all
![]() $1\leq i\leq m$
,
$1\leq i\leq m$
,
 $$\begin{align*}\bigcap_{j=1}^r \operatorname{\mathrm{\text{conv}}}\left(\{x_{a_1}^{b_1},\ldots,x_{a_n}^{b_n},x_{a_{n+i}}^{b_{n+i}}\}\cap P_j\right) = \bigcap_{j=1}^r \operatorname{\mathrm{\text{conv}}}\left((B\cup \{x_{a_{n+i}}\})\cap A_j\right)\neq \emptyset, \end{align*}$$
$$\begin{align*}\bigcap_{j=1}^r \operatorname{\mathrm{\text{conv}}}\left(\{x_{a_1}^{b_1},\ldots,x_{a_n}^{b_n},x_{a_{n+i}}^{b_{n+i}}\}\cap P_j\right) = \bigcap_{j=1}^r \operatorname{\mathrm{\text{conv}}}\left((B\cup \{x_{a_{n+i}}\})\cap A_j\right)\neq \emptyset, \end{align*}$$
as wanted.
Remark 6.4. For any point set in
![]() ${\mathbb R}^d$
of size larger than
${\mathbb R}^d$
of size larger than
![]() $(r-1)(d+1)$
, Theorem 1.10 guarantees the existence of a partition into r parts with Tverberg center of size at most
$(r-1)(d+1)$
, Theorem 1.10 guarantees the existence of a partition into r parts with Tverberg center of size at most
![]() $(r-1)(d+1)$
. Note, however, that the same point set may have other Tverberg partitions without such a center (see Figure 1).
$(r-1)(d+1)$
. Note, however, that the same point set may have other Tverberg partitions without such a center (see Figure 1).

Figure 1 Two Tverberg partitions of nine points in the plane into three parts. The partition on the left does not have a Tverberg center of size
![]() $6$
, while the partition on the right has one:
$6$
, while the partition on the right has one:
![]() $\{v_2,v_4,v_5,v_6,v_7,v_9\}$
.
$\{v_2,v_4,v_5,v_6,v_7,v_9\}$
.
Let
![]() $A\subset {\mathbb R}^d$
be a finite set of points. We say that a partition
$A\subset {\mathbb R}^d$
be a finite set of points. We say that a partition
![]() $A_1,\ldots ,A_r$
of A is a Tverberg partition with tolerance t if
$A_1,\ldots ,A_r$
of A is a Tverberg partition with tolerance t if
 $$\begin{align*}\bigcap_{i=1}^r \operatorname{\mathrm{\text{conv}}}(A_i\setminus C)\neq\emptyset, \end{align*}$$
$$\begin{align*}\bigcap_{i=1}^r \operatorname{\mathrm{\text{conv}}}(A_i\setminus C)\neq\emptyset, \end{align*}$$
for any
![]() $C\subset A$
of size at most t. In other words, the partition has tolerance t if it remains a Tverberg partition even after removing any t points from A. Larman showed in [Reference Larman12] that any
$C\subset A$
of size at most t. In other words, the partition has tolerance t if it remains a Tverberg partition even after removing any t points from A. Larman showed in [Reference Larman12] that any
![]() $2d+3$
points in
$2d+3$
points in
![]() ${\mathbb R}^d$
have a Tverberg partition into two parts (that is, a Radon partition) with tolerance
${\mathbb R}^d$
have a Tverberg partition into two parts (that is, a Radon partition) with tolerance
![]() $1$
. This was later extended by García-Colín ([Reference García-Colín6, Reference García-Colín and Larman7]) who showed that any
$1$
. This was later extended by García-Colín ([Reference García-Colín6, Reference García-Colín and Larman7]) who showed that any
![]() $(t+1)(d+1)+1$
points in
$(t+1)(d+1)+1$
points in
![]() ${\mathbb R}^d$
have a Radon partition with tolerance t, and by Soberón and Strausz in [Reference Soberón and Strausz21], who showed that any
${\mathbb R}^d$
have a Radon partition with tolerance t, and by Soberón and Strausz in [Reference Soberón and Strausz21], who showed that any
![]() $(t+1)(r-1)(d+1)+1$
points in
$(t+1)(r-1)(d+1)+1$
points in
![]() ${\mathbb R}^d$
have a Tverberg partition into r parts with tolerance t. Note that this bound is not sharp in general: In [Reference García-Colín, Raggi and Roldán-Pensado8], it was shown that any set of
${\mathbb R}^d$
have a Tverberg partition into r parts with tolerance t. Note that this bound is not sharp in general: In [Reference García-Colín, Raggi and Roldán-Pensado8], it was shown that any set of
![]() $rt+o(t)$
points in
$rt+o(t)$
points in
![]() ${\mathbb R}^d$
has a Tverberg partition into r parts with tolerance t, giving an improved bound for large values of t (see [Reference Soberón20] for a further improvement of this bound). In [Reference Mulzer and Stein14], an improved bound was given in the case
${\mathbb R}^d$
has a Tverberg partition into r parts with tolerance t, giving an improved bound for large values of t (see [Reference Soberón20] for a further improvement of this bound). In [Reference Mulzer and Stein14], an improved bound was given in the case
![]() $d=1$
, and in the case
$d=1$
, and in the case
![]() $d=2$
for some values of
$d=2$
for some values of
![]() $r,t$
.
$r,t$
.
It was brought to our attention by Andreas Holmsen that one can recover Soberón and Strausz’s result as a consequence of Theorem 1.10, in the following way:
Theorem 1.11 (Soberón-Strausz [Reference Soberón and Strausz21, Theorem 1]).
Let
![]() $d\geq 1$
,
$d\geq 1$
,
![]() $r\geq 2$
and
$r\geq 2$
and
![]() $t\geq 0$
. Let
$t\geq 0$
. Let
![]() $A\subset {\mathbb R}^d$
be finite set of points of size at least
$A\subset {\mathbb R}^d$
be finite set of points of size at least
![]() $(t+1)(r-1)(d+1)+1$
. Then, A has a Tverberg partition into r parts with tolerance t.
$(t+1)(r-1)(d+1)+1$
. Then, A has a Tverberg partition into r parts with tolerance t.
Proof. We argue by induction on t. For
![]() $t=0$
, the claim is just Tverberg’s theorem. Assume
$t=0$
, the claim is just Tverberg’s theorem. Assume
![]() $t\geq 1$
. By Theorem 1.10, there exists a partition
$t\geq 1$
. By Theorem 1.10, there exists a partition
![]() $A_1,\ldots ,A_r$
of A and a set
$A_1,\ldots ,A_r$
of A and a set
![]() $B\subset A$
of size
$B\subset A$
of size
![]() $(r-1)(d+1)$
such that
$(r-1)(d+1)$
such that
 $$\begin{align*}\bigcap_{i=1}^r \operatorname{\mathrm{\text{conv}}}((B\cup\{p\})\cap A_i)\neq\emptyset \end{align*}$$
$$\begin{align*}\bigcap_{i=1}^r \operatorname{\mathrm{\text{conv}}}((B\cup\{p\})\cap A_i)\neq\emptyset \end{align*}$$
for any
![]() $p\in A\setminus B$
. Note that
$p\in A\setminus B$
. Note that
![]() $|A\setminus B|\geq t(r-1)(d+1)+1$
. Therefore, by the induction hypothesis, there is a Tverberg partition
$|A\setminus B|\geq t(r-1)(d+1)+1$
. Therefore, by the induction hypothesis, there is a Tverberg partition
![]() $B_1,\ldots ,B_r$
of
$B_1,\ldots ,B_r$
of
![]() $A\setminus B$
with tolerance
$A\setminus B$
with tolerance
![]() $t-1$
.
$t-1$
.
We denote by
![]() $S_r$
the set of permutations of
$S_r$
the set of permutations of
![]() $[r]$
. Since
$[r]$
. Since
![]() $|A\setminus B|> t(r-1)(d+1)\geq tr$
, we have
$|A\setminus B|> t(r-1)(d+1)\geq tr$
, we have
 $$ \begin{align*} \frac{1}{r!}\sum_{\pi\in S_r} |\cup_{i=1}^r A_i\cap B_{\pi(i)}| &=\frac{1}{r!}\sum_{\pi\in S_r} \sum_{i=1}^r |A_i\cap B_{\pi(i)}| =\frac{1}{r!} \sum_{i=1}^r \sum_{\pi\in S_r} |A_i\cap B_{\pi(i)}| \\ &=\frac{1}{r!} \sum_{i=1}^r (r-1)! |A_i\setminus B| = \frac{|A\setminus B|}{r}>t. \end{align*} $$
$$ \begin{align*} \frac{1}{r!}\sum_{\pi\in S_r} |\cup_{i=1}^r A_i\cap B_{\pi(i)}| &=\frac{1}{r!}\sum_{\pi\in S_r} \sum_{i=1}^r |A_i\cap B_{\pi(i)}| =\frac{1}{r!} \sum_{i=1}^r \sum_{\pi\in S_r} |A_i\cap B_{\pi(i)}| \\ &=\frac{1}{r!} \sum_{i=1}^r (r-1)! |A_i\setminus B| = \frac{|A\setminus B|}{r}>t. \end{align*} $$
Therefore, there is some
![]() $\pi \in S_r$
such that
$\pi \in S_r$
such that
![]() $|\cup _{i=1}^r A_i\cap B_{\pi (i)}|\geq t+1$
. Let
$|\cup _{i=1}^r A_i\cap B_{\pi (i)}|\geq t+1$
. Let
![]() $D=\cup _{i=1}^r A_i\cap B_{\pi (i)}$
. We define a new partition
$D=\cup _{i=1}^r A_i\cap B_{\pi (i)}$
. We define a new partition
![]() $\tilde {A}_1,\ldots ,\tilde {A}_r$
of A by
$\tilde {A}_1,\ldots ,\tilde {A}_r$
of A by
for all
![]() $1\leq i\leq r$
. Note that
$1\leq i\leq r$
. Note that
![]() $\tilde {A}_i\cap D=A_i\cap D$
for all i.
$\tilde {A}_i\cap D=A_i\cap D$
for all i.
We are left to show that
![]() $\tilde {A}_1,\ldots ,\tilde {A}_r$
is a Tverberg partition of A with tolerance t. Let
$\tilde {A}_1,\ldots ,\tilde {A}_r$
is a Tverberg partition of A with tolerance t. Let
![]() $C\subset A$
be a subset of size at most t. We divide into two cases. First, assume that C is disjoint from B. Then, since
$C\subset A$
be a subset of size at most t. We divide into two cases. First, assume that C is disjoint from B. Then, since
![]() $|C|\leq t$
and
$|C|\leq t$
and
![]() $|D|\geq t+1$
, there is some
$|D|\geq t+1$
, there is some
![]() $p\in D\setminus C$
. We obtain
$p\in D\setminus C$
. We obtain
 $$ \begin{align*} \bigcap_{i=1}^r \operatorname{\mathrm{\text{conv}}}(\tilde{A_i}\setminus C) \supset \bigcap_{i=1}^r \operatorname{\mathrm{\text{conv}}}&((\tilde{A_i}\cap (B\cup D))\setminus C) \\ & = \bigcap_{i=1}^r \operatorname{\mathrm{\text{conv}}}((A_i\cap(B\cup D) )\setminus C) \supset \bigcap_{i=1}^r \operatorname{\mathrm{\text{conv}}}(A_i\cap(B\cup \{p\}))\neq \emptyset, \end{align*} $$
$$ \begin{align*} \bigcap_{i=1}^r \operatorname{\mathrm{\text{conv}}}(\tilde{A_i}\setminus C) \supset \bigcap_{i=1}^r \operatorname{\mathrm{\text{conv}}}&((\tilde{A_i}\cap (B\cup D))\setminus C) \\ & = \bigcap_{i=1}^r \operatorname{\mathrm{\text{conv}}}((A_i\cap(B\cup D) )\setminus C) \supset \bigcap_{i=1}^r \operatorname{\mathrm{\text{conv}}}(A_i\cap(B\cup \{p\}))\neq \emptyset, \end{align*} $$
as desired. Next, assume that
![]() $C\cap B\neq \emptyset $
. Let
$C\cap B\neq \emptyset $
. Let
![]() $C'=C\cap (A\setminus B)$
. Then
$C'=C\cap (A\setminus B)$
. Then
![]() $|C'|\leq t-1$
, and therefore, since
$|C'|\leq t-1$
, and therefore, since
![]() $B_1,\ldots ,B_r$
is a Tverberg partition of
$B_1,\ldots ,B_r$
is a Tverberg partition of
![]() $A\setminus B$
with tolerance
$A\setminus B$
with tolerance
![]() $t-1$
, we obtain
$t-1$
, we obtain
 $$\begin{align*}\bigcap_{i=1}^r \operatorname{\mathrm{\text{conv}}}(\tilde{A_i}\setminus C) \supset \bigcap_{i=1}^r\operatorname{\mathrm{\text{conv}}}((\tilde{A_i}\cap (A\setminus B))\setminus C') =\bigcap_{i=1}^r\operatorname{\mathrm{\text{conv}}}( B_{\pi(i)}\setminus C') =\bigcap_{i=1}^r\operatorname{\mathrm{\text{conv}}}( B_{i}\setminus C') \neq \emptyset. \end{align*}$$
$$\begin{align*}\bigcap_{i=1}^r \operatorname{\mathrm{\text{conv}}}(\tilde{A_i}\setminus C) \supset \bigcap_{i=1}^r\operatorname{\mathrm{\text{conv}}}((\tilde{A_i}\cap (A\setminus B))\setminus C') =\bigcap_{i=1}^r\operatorname{\mathrm{\text{conv}}}( B_{\pi(i)}\setminus C') =\bigcap_{i=1}^r\operatorname{\mathrm{\text{conv}}}( B_{i}\setminus C') \neq \emptyset. \end{align*}$$
Thus,
![]() $\tilde {A}_1,\ldots ,\tilde {A}_r$
is a Tverberg partition of A with tolerance t, as wanted.
$\tilde {A}_1,\ldots ,\tilde {A}_r$
is a Tverberg partition of A with tolerance t, as wanted.
7 Concluding remarks
It would be interesting to prove a stronger version of Theorem 1.7, analogous to Theorem 1.6:
Conjecture 7.1. Let
![]() $d\geq 1$
,
$d\geq 1$
,
![]() $r\geq d+1$
,
$r\geq d+1$
,
![]() $1\leq m\leq r$
and
$1\leq m\leq r$
and
![]() $m\leq k\leq \min \{m+d,r\}$
be integers. Let V be a finite set with
$m\leq k\leq \min \{m+d,r\}$
be integers. Let V be a finite set with
![]() $|V|\geq \max \{m+d,r\}$
. Let X be a d-Leray simplicial complex on vertex set V, and let M be a matroid of rank r on vertex set V with rank function
$|V|\geq \max \{m+d,r\}$
. Let X be a d-Leray simplicial complex on vertex set V, and let M be a matroid of rank r on vertex set V with rank function
![]() $\rho $
.
$\rho $
.
Assume that for every
![]() $U=\{u_1,\ldots ,u_d,v_1,\ldots ,v_m\}\subset V$
with
$U=\{u_1,\ldots ,u_d,v_1,\ldots ,v_m\}\subset V$
with
![]() $\rho (U)\geq k$
, there is some
$\rho (U)\geq k$
, there is some
![]() $i\in [m]$
such that
$i\in [m]$
such that
![]() $\{u_1,\ldots ,u_d,v_i\}\in X$
. Then, there is some
$\{u_1,\ldots ,u_d,v_i\}\in X$
. Then, there is some
![]() $\tau \in X$
such that
$\tau \in X$
such that
![]() $\rho (V\setminus \tau )\leq k-1$
.
$\rho (V\setminus \tau )\leq k-1$
.
Another interesting question, suggested to us by Florian Frick, is whether a version of Theorem 1.10 holds in the context of the topological Tverberg theorem. That is,
Conjecture 7.2. Let
![]() $d\geq 1$
,
$d\geq 1$
,
![]() $r\geq 2$
a prime power, and
$r\geq 2$
a prime power, and
![]() $n=(r-1)(d+1)$
. Let
$n=(r-1)(d+1)$
. Let
![]() $N>n$
, and let
$N>n$
, and let
![]() $\Delta _N$
be the N-dimensional simplex. Then, for every continuous map
$\Delta _N$
be the N-dimensional simplex. Then, for every continuous map
![]() $ f: \Delta _N\to {\mathbb R}^d, $
there exist r pairwise disjoint faces
$ f: \Delta _N\to {\mathbb R}^d, $
there exist r pairwise disjoint faces
![]() $F_1,\ldots ,F_r$
of
$F_1,\ldots ,F_r$
of
![]() $\Delta _N$
, and an
$\Delta _N$
, and an
![]() $(n-1)$
-dimensional face F of
$(n-1)$
-dimensional face F of
![]() $\Delta _N$
such that, for each n-dimensional face
$\Delta _N$
such that, for each n-dimensional face
![]() $F'$
of
$F'$
of
![]() $\Delta _N$
containing F,
$\Delta _N$
containing F,
![]() $\cap _{i=1}^r f(F_i\cap F')\neq \emptyset $
.
$\cap _{i=1}^r f(F_i\cap F')\neq \emptyset $
.
Acknowledgements
We thank Florian Frick, Andreas Holmsen and Roy Meshulam for their helpful comments and suggestions. We thank Andreas Holmsen for sharing with us his argument for deriving Theorem 1.11 from Theorem 1.10. We also thank an anonymous referee for carefully reading our manuscript and pointing out a few typos.
Competing interest
The authors have no competing interest to declare.
Funding statement
M. Kim was supported by the Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education (NRF-2022R1F1A1063424).