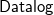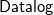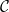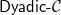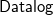1 Introduction
In ontology-based query answering, a conjunctive query is typically evaluated over a logical theory consisting of a relational database paired with an ontology. Description logics (Baader et al. Reference Baader, Calvanese, McGuinness, Nardi and Patel-Schneider2003) and existential rules – a.k.a. tuple generating dependencies, or
![]() ${{\textsf{Datalog}}}^\pm$
rules – (Baget et al. Reference Baget, Leclère, Mugnier and Salvat2011) are the main languages used to specify ontologies. In particular, the latter are essentially classical datalog rules (Abiteboul et al. Reference Abiteboul, Hull and Vianu1995) extended with existential quantified variables in rule-heads. The presence of existential quantification in the head of rules, however, makes query answering undecidable in the general case. To overcome this limitation, in the last two decades, a number of classes of existential rules – based on both semantic and syntactic conditions – that guarantee the decidability of query answering have been proposed. Concerning the semantic conditions, we recall finite expansions sets, finite treewidth sets, finite unification sets, and strongly parsimonious sets (Baget et al. Reference Baget, Leclère, Mugnier and Salvat2009; Baget et al. Reference Baget, Leclère, Mugnier and Salvat2011; Leone et al. Reference Leone, Manna, Terracina and Veltri2019). Each of these classes encompasses a number of concrete classes based on syntactic conditions (Baget et al. Reference Baget, Leclère, Mugnier and Salvat2011; Calì et al. Reference Calì, Gottlob and Kifer2013; Fagin et al. Reference Fagin, Kolaitis, Miller and Popa2005; Krötzsch and Rudolph 2011; Ceri et al. Reference Ceri, Gottlob and Tanca1989; Leone et al. Reference Leone, Manna, Terracina and Veltri2019; Gottlob and Pieris 2015; Baldazzi et al. Reference Baldazzi, Bellomarini, Favorito and Sallinger2022; Calì et al. Reference Calì, Gottlob and Pieris2012b; Calì et al. Reference Calì, Gottlob and Lukasiewicz2012a; Gogacz and Marcinkowski 2017; Johnson and Klug Reference Johnson and Klug1984). Table 1 summarizes these classes and their computational complexity with respect to query answering, by distinguishing between combined complexity (the input consists of a database, an ontology, a conjunctive query, and a tuple of constants) and data complexity (only a database is given as input, whereas the remaining parameters are considered fixed).
${{\textsf{Datalog}}}^\pm$
rules – (Baget et al. Reference Baget, Leclère, Mugnier and Salvat2011) are the main languages used to specify ontologies. In particular, the latter are essentially classical datalog rules (Abiteboul et al. Reference Abiteboul, Hull and Vianu1995) extended with existential quantified variables in rule-heads. The presence of existential quantification in the head of rules, however, makes query answering undecidable in the general case. To overcome this limitation, in the last two decades, a number of classes of existential rules – based on both semantic and syntactic conditions – that guarantee the decidability of query answering have been proposed. Concerning the semantic conditions, we recall finite expansions sets, finite treewidth sets, finite unification sets, and strongly parsimonious sets (Baget et al. Reference Baget, Leclère, Mugnier and Salvat2009; Baget et al. Reference Baget, Leclère, Mugnier and Salvat2011; Leone et al. Reference Leone, Manna, Terracina and Veltri2019). Each of these classes encompasses a number of concrete classes based on syntactic conditions (Baget et al. Reference Baget, Leclère, Mugnier and Salvat2011; Calì et al. Reference Calì, Gottlob and Kifer2013; Fagin et al. Reference Fagin, Kolaitis, Miller and Popa2005; Krötzsch and Rudolph 2011; Ceri et al. Reference Ceri, Gottlob and Tanca1989; Leone et al. Reference Leone, Manna, Terracina and Veltri2019; Gottlob and Pieris 2015; Baldazzi et al. Reference Baldazzi, Bellomarini, Favorito and Sallinger2022; Calì et al. Reference Calì, Gottlob and Pieris2012b; Calì et al. Reference Calì, Gottlob and Lukasiewicz2012a; Gogacz and Marcinkowski 2017; Johnson and Klug Reference Johnson and Klug1984). Table 1 summarizes these classes and their computational complexity with respect to query answering, by distinguishing between combined complexity (the input consists of a database, an ontology, a conjunctive query, and a tuple of constants) and data complexity (only a database is given as input, whereas the remaining parameters are considered fixed).
Table 1. Computational complexity of query answering

[1] Baget et al. (2011); [2] Calì et al. (2013); [3] Fagin et al. (2005); [4] Krötzsch and Rudolph (2011); [5] Ceri et al. (1989); [6] Leone et al. (2019); [7] Gottlob and Pieris (2015); [8] Baldazzi et al. (2022); [9] Calì et al. (2012b); [10] Calì et al. (2012a); [11] Gogacz and Marcinkowski (2017); [12] Johnson and Klug (1984).
Unfortunately, on the one side, despite the fact that existential rules generalize datalog rules, only some of these syntactic classes fully encompass Datalog and, in some cases, this even comes at the price of higher computational complexity of query answering. Moreover, on the other side, expressive classes typically need ad hoc reasoners without being able to exploit mature tools developed for classes exhibiting lower expressiveness.
With the aim of mitigating the two aforementioned shortcomings, this paper introduces a novel general syntactic condition that allows to define, systematically and in a uniform way, from any decidable class
![]() $\mathcal{C}$
of existential rules, a new class called
$\mathcal{C}$
of existential rules, a new class called
![]() ${{\textsf{Dyadic-}\mathcal{C}}}$
that enjoys the following properties: (i) it is decidable; (ii) it generalizes Datalog;Footnote 1 (iii) it generalizes
${{\textsf{Dyadic-}\mathcal{C}}}$
that enjoys the following properties: (i) it is decidable; (ii) it generalizes Datalog;Footnote 1 (iii) it generalizes
![]() $\mathcal{C}$
; and (iv) it can effectively exploit any reasoner for query answering over
$\mathcal{C}$
; and (iv) it can effectively exploit any reasoner for query answering over
![]() $\mathcal{C}$
. In particular, let
$\mathcal{C}$
. In particular, let
![]() $\mathbb{C}_d$
(resp.,
$\mathbb{C}_d$
(resp.,
![]() $\mathbb{C}_c$
) be the data (resp., combined) complexity of query answering over
$\mathbb{C}_c$
) be the data (resp., combined) complexity of query answering over
![]() ${{\mathcal{C}}}$
, query answering over
${{\mathcal{C}}}$
, query answering over
![]() ${{\textsf{Dyadic-}\mathcal{C}}}$
is
${{\textsf{Dyadic-}\mathcal{C}}}$
is
![]() ${ \textbf{PTIME}}^{\mathbb{C}_d}$
(resp.,
${ \textbf{PTIME}}^{\mathbb{C}_d}$
(resp.,
![]() ${ \textbf{EXPTIME}}^{\mathbb{C}_c}$
provided that there is at least an exponential jump from
${ \textbf{EXPTIME}}^{\mathbb{C}_c}$
provided that there is at least an exponential jump from
![]() $\mathbb{C}_d$
to
$\mathbb{C}_d$
to
![]() $\mathbb{C}_c$
). Since all the classes reported in Table 1 comply with the exponential jump assumption, we get the following: (a) whenever
$\mathbb{C}_c$
). Since all the classes reported in Table 1 comply with the exponential jump assumption, we get the following: (a) whenever
![]() ${\mathbb{C}_d} \supseteq { \textbf{PTIME}}$
(entries 1–8 of Table 1), then query answering over
${\mathbb{C}_d} \supseteq { \textbf{PTIME}}$
(entries 1–8 of Table 1), then query answering over
![]() ${{\textsf{Dyadic-}\mathcal{C}}}$
is complete for
${{\textsf{Dyadic-}\mathcal{C}}}$
is complete for
![]() $\mathbb{C}_d$
(resp.,
$\mathbb{C}_d$
(resp.,
![]() $\mathbb{C}_c$
); (b) in all the remaining cases (entries 9-12 of Table 1), query answering over
$\mathbb{C}_c$
); (b) in all the remaining cases (entries 9-12 of Table 1), query answering over
![]() ${{\textsf{Dyadic-}\mathcal{C}}}$
is complete for
${{\textsf{Dyadic-}\mathcal{C}}}$
is complete for
![]() ${ \textbf{PTIME}}$
(resp.,
${ \textbf{PTIME}}$
(resp.,
![]() ${ \textbf{EXPTIME}}$
), namely it has the same complexity of query answering over
${ \textbf{EXPTIME}}$
), namely it has the same complexity of query answering over
![]() ${{\textsf{Datalog}}}$
.
${{\textsf{Datalog}}}$
.
Concerning the key principle at the heart of this new general syntactic condition, basically, an ontology
![]() $\Sigma$
belongs to
$\Sigma$
belongs to
![]() ${{\textsf{Dyadic-}\mathcal{C}}}$
if one can easily construct a pair
${{\textsf{Dyadic-}\mathcal{C}}}$
if one can easily construct a pair
![]() $(\Sigma_\mathrm{HG}, \Sigma_\mathcal{C})$
of ontologies, called dyadic, such that: (i)
$(\Sigma_\mathrm{HG}, \Sigma_\mathcal{C})$
of ontologies, called dyadic, such that: (i)
![]() $\Sigma_\mathrm{HG} \cup \Sigma_\mathcal{C}$
is equivalent to
$\Sigma_\mathrm{HG} \cup \Sigma_\mathcal{C}$
is equivalent to
![]() $\Sigma$
with respect to query answering; (ii)
$\Sigma$
with respect to query answering; (ii)
![]() $\Sigma_\mathcal{C} \in \mathcal{C}$
; and (iii)
$\Sigma_\mathcal{C} \in \mathcal{C}$
; and (iii)
![]() $\Sigma_\mathrm{HG}$
is a set rules called head-ground with respect to
$\Sigma_\mathrm{HG}$
is a set rules called head-ground with respect to
![]() $\Sigma_\mathrm{HG} \cup \Sigma_\mathcal{C}$
(Gottlob and Pieris 2015). Intuitively,
$\Sigma_\mathrm{HG} \cup \Sigma_\mathcal{C}$
(Gottlob and Pieris 2015). Intuitively,
![]() $\Sigma_\mathrm{HG}$
satisfies the following properties: (1) it belongs to
$\Sigma_\mathrm{HG}$
satisfies the following properties: (1) it belongs to
![]() $\mathsf{Datalog}$
; (2) for each database D, the chase procedure (Deutsch et al. 2008) over
$\mathsf{Datalog}$
; (2) for each database D, the chase procedure (Deutsch et al. 2008) over
![]() $D \cup \Sigma_\mathrm{HG} \cup \Sigma_\mathcal{C}$
never generates atoms containing null-values via rules of
$D \cup \Sigma_\mathrm{HG} \cup \Sigma_\mathcal{C}$
never generates atoms containing null-values via rules of
![]() $\Sigma_\mathrm{HG}$
; (3) head-predicates of
$\Sigma_\mathrm{HG}$
; (3) head-predicates of
![]() $\Sigma_\mathrm{HG}$
and body-predicates of
$\Sigma_\mathrm{HG}$
and body-predicates of
![]() $\Sigma_\mathrm{HG}$
are disjoint; and (4) head-predicates of
$\Sigma_\mathrm{HG}$
are disjoint; and (4) head-predicates of
![]() $\Sigma_\mathrm{HG}$
and head-predicates of
$\Sigma_\mathrm{HG}$
and head-predicates of
![]() $\Sigma_\mathcal{C}$
are disjoint. Finally, since
$\Sigma_\mathcal{C}$
are disjoint. Finally, since
![]() ${{\textsf{Dyadic-}\mathcal{C}}}$
is well-defined even if
${{\textsf{Dyadic-}\mathcal{C}}}$
is well-defined even if
![]() ${{\mathcal{C}}}$
is a class of existential rules based on some semantic conditions and, if so, since query answering is still decidable over
${{\mathcal{C}}}$
is a class of existential rules based on some semantic conditions and, if so, since query answering is still decidable over
![]() ${{\textsf{Dyadic-}\mathcal{C}}}$
, then – in analogy with the existing semantic classes – the union of all the
${{\textsf{Dyadic-}\mathcal{C}}}$
, then – in analogy with the existing semantic classes – the union of all the
![]() ${{\textsf{Dyadic-}\mathcal{C}}}$
classes are called dyadic decomposable sets.
${{\textsf{Dyadic-}\mathcal{C}}}$
classes are called dyadic decomposable sets.
The article is a revised version of an earlier workshop paper (Gottlob et al. 2022). Specifically, the content that was previously presented in a single preliminary section has been expanded and reorganized into two longer separate sections, namely Sections 2 and 3. These sections now contain the necessary background information, ensuring that the paper is self-contained. Furthermore, the previous notion of “dyadic decomposition” has evolved into the novel notion of a “Dyadic Pair of TGDs”, which is discussed in Section 4. This new notion captures the essential properties of dyadic decompositions and also generalizes the notion of ontology, providing new perspectives and insights. Additionally, in Section 5, the notion of “Dyadic Decomposable Sets” is now supported by a canonical concrete algorithm that produces a Dyadic Pair of TGDs from each Dyadic Decomposable Set. The revisions also lead to new results regarding decidability and complexity. First, if
![]() $\mathcal{C}$
is an abstract (resp., concrete) and decidable class, then
$\mathcal{C}$
is an abstract (resp., concrete) and decidable class, then
![]() ${{\textsf{Dyadic-}\mathcal{C}}}$
is now also an abstract (resp., concrete) and decidable class. Second, the relationship between Datalog and any
${{\textsf{Dyadic-}\mathcal{C}}}$
is now also an abstract (resp., concrete) and decidable class. Second, the relationship between Datalog and any
![]() ${{\textsf{Dyadic-}\mathcal{C}}}$
is made explicit, emphasizing the low expressive power required for
${{\textsf{Dyadic-}\mathcal{C}}}$
is made explicit, emphasizing the low expressive power required for
![]() $\mathcal{C}$
to ensure that
$\mathcal{C}$
to ensure that
![]() ${{\textsf{Dyadic-}\mathcal{C}}}$
fully encompasses Datalog. Finally, the computational complexity analysis is completed in Section 6, where both data and combined complexity for any
${{\textsf{Dyadic-}\mathcal{C}}}$
fully encompasses Datalog. Finally, the computational complexity analysis is completed in Section 6, where both data and combined complexity for any
![]() ${{\textsf{Dyadic-}\mathcal{C}}}$
class are systematically studied.
${{\textsf{Dyadic-}\mathcal{C}}}$
class are systematically studied.
2 Preliminaries
In this section, we introduce the syntax and the semantics of the class of rules that generalizes Datalog with existential quantifiers in rule-heads. Regarding computational complexity, we assume the reader is familiar with the basic complexity classes used in the subsequent sections:
![]() ${{{ \textbf{AC}_0}}}$
${{{ \textbf{AC}_0}}}$
![]() $\subseteq$
PTIME
$\subseteq$
PTIME
![]() $\subseteq$
NP
$\subseteq$
NP
![]() $\subseteq$
PSPACE
$\subseteq$
PSPACE
![]() $\subseteq$
EXPTIME
$\subseteq$
EXPTIME
![]() $\subseteq$
2EXPTIME. Moreover, for a complexity class
$\subseteq$
2EXPTIME. Moreover, for a complexity class
![]() $\mathbb{C}$
, we denote by
$\mathbb{C}$
, we denote by
![]() ${ \textbf{PTIME}}^{\mathbb{C}}$
(resp.,
${ \textbf{PTIME}}^{\mathbb{C}}$
(resp.,
![]() ${ \textbf{EXPTIME}}^{\mathbb{C}}$
) the class of decision problems that can be solved by an oracle Turing machine operating in polynomial (resp., exponential) time with the aid of an oracle that decides a problem in
${ \textbf{EXPTIME}}^{\mathbb{C}}$
) the class of decision problems that can be solved by an oracle Turing machine operating in polynomial (resp., exponential) time with the aid of an oracle that decides a problem in
![]() $\mathbb{C}$
.
$\mathbb{C}$
.
2.1 Basics on relational structures
Fix three pairwise disjoint lexicographically enumerable infinite sets
![]() $\mathsf{C}$
of constants,
$\mathsf{C}$
of constants,
![]() $\mathsf{N}$
of nulls (
$\mathsf{N}$
of nulls (
![]() $\varphi$
,
$\varphi$
,
![]() $\varphi_0$
,
$\varphi_0$
,
![]() $\varphi_1$
, …), and
$\varphi_1$
, …), and
![]() $\mathsf{V}$
of variables (x, y, z, and variations thereof). Their union is denoted by
$\mathsf{V}$
of variables (x, y, z, and variations thereof). Their union is denoted by
![]() $\mathsf{T}$
and its elements are called terms. For any integer
$\mathsf{T}$
and its elements are called terms. For any integer
![]() $k \geq 0$
, we may write [k] for the set
$k \geq 0$
, we may write [k] for the set
![]() $ \{1,..., k \}$
; in particular, as usual, if
$ \{1,..., k \}$
; in particular, as usual, if
![]() $k = 0$
, then
$k = 0$
, then
![]() $[k] = \emptyset$
.
$[k] = \emptyset$
.
An atom
![]() $\underline{a}$
is an expression of the form
$\underline{a}$
is an expression of the form
![]() $P(\textbf{t})$
, where
$P(\textbf{t})$
, where
![]() $\mathit{preds}(\underline{a})=P$
is a (relational) predicate,
$\mathit{preds}(\underline{a})=P$
is a (relational) predicate,
![]() $\textbf{t}=t_1,..., t_k$
is a tuple of terms
$\textbf{t}=t_1,..., t_k$
is a tuple of terms
![]() $\mathit{arity}(\underline{a}) = \mathit{arity}(P)=k \geq 0$
is the arity of both
$\mathit{arity}(\underline{a}) = \mathit{arity}(P)=k \geq 0$
is the arity of both
![]() $\underline{a}$
and P, and
$\underline{a}$
and P, and
![]() $\underline{a}[i]$
denotes the i-th term
$\underline{a}[i]$
denotes the i-th term
![]() $\textbf{t}[i] = t_i$
of
$\textbf{t}[i] = t_i$
of
![]() $\underline{a}$
, for each
$\underline{a}$
, for each
![]() $i \in [k]$
. In particular, if
$i \in [k]$
. In particular, if
![]() $k = 0$
, then
$k = 0$
, then
![]() $\textbf{t}$
is the empty tuple and
$\textbf{t}$
is the empty tuple and
![]() $\underline{a} = P()$
. By
$\underline{a} = P()$
. By
![]() $\mathit{consts}(\underline{a})$
and
$\mathit{consts}(\underline{a})$
and
![]() $\mathit{vars}(\underline{a})$
we denote, respectively, the set of constants and variables occurring in
$\mathit{vars}(\underline{a})$
we denote, respectively, the set of constants and variables occurring in
![]() $\underline{a}$
. A fact is an atom that contains only constants.
$\underline{a}$
. A fact is an atom that contains only constants.
A (relational) schema
![]() $\mathbf{S}$
is a finite set of predicates, each with its own arity. The set of positions of
$\mathbf{S}$
is a finite set of predicates, each with its own arity. The set of positions of
![]() $\mathbf{S}$
, denoted by
$\mathbf{S}$
, denoted by
![]() $\mathit{pos}(\mathbf{S})$
, is defined as the set
$\mathit{pos}(\mathbf{S})$
, is defined as the set
![]() $\{P[i] \ | \ P \in \mathbf{S}~\wedge~ 1 \leq i \leq \mathit{arity}(P)\}$
, where each P[i] denotes the i-th position of P. A (relational) structure over
$\{P[i] \ | \ P \in \mathbf{S}~\wedge~ 1 \leq i \leq \mathit{arity}(P)\}$
, where each P[i] denotes the i-th position of P. A (relational) structure over
![]() $\mathbf{S}$
is any (possibly infinite) set of atoms using only predicates from
$\mathbf{S}$
is any (possibly infinite) set of atoms using only predicates from
![]() $\mathbf{S}$
. The domain of a structure S, denoted by
$\mathbf{S}$
. The domain of a structure S, denoted by
![]() $\mathit{dom}(S)$
, is the set of all the terms forming the atoms of S. An instance over
$\mathit{dom}(S)$
, is the set of all the terms forming the atoms of S. An instance over
![]() $\mathbf{S}$
is any structure I over
$\mathbf{S}$
is any structure I over
![]() $\mathbf{S}$
such that
$\mathbf{S}$
such that
![]() $\mathit{dom}(I) \subseteq \mathsf{C} \cup \mathsf{N}$
. A database over
$\mathit{dom}(I) \subseteq \mathsf{C} \cup \mathsf{N}$
. A database over
![]() $\mathbf{S}$
is any finite instance over
$\mathbf{S}$
is any finite instance over
![]() $\mathbf{S}$
containing only facts. The active domain of an instance I, denoted by
$\mathbf{S}$
containing only facts. The active domain of an instance I, denoted by
![]() $\mathit{dom}(I)$
, is the set of all the terms occurring in I, whereas the Herbrand Base of I, denoted by
$\mathit{dom}(I)$
, is the set of all the terms occurring in I, whereas the Herbrand Base of I, denoted by
![]() ${{\mathit{HB}}}(I)$
, is the set of all the atoms that can be formed using the predicate symbols of
${{\mathit{HB}}}(I)$
, is the set of all the atoms that can be formed using the predicate symbols of
![]() $\mathbf{S}$
and terms of
$\mathbf{S}$
and terms of
![]() $\mathit{dom}(I)$
.
$\mathit{dom}(I)$
.
Consider two sets of terms
![]() $T_1$
and
$T_1$
and
![]() $T_2$
and a map
$T_2$
and a map
![]() $\mu : T_1 \rightarrow T_2$
. Given a set T of terms, the restriction of
$\mu : T_1 \rightarrow T_2$
. Given a set T of terms, the restriction of
![]() $\mu$
with respect to T is the map
$\mu$
with respect to T is the map
![]() $\mu|_{T} = \{t \mapsto \mu(t):t \in T_1 \cap T\}$
. An extension of
$\mu|_{T} = \{t \mapsto \mu(t):t \in T_1 \cap T\}$
. An extension of
![]() $\mu$
is any map
$\mu$
is any map
![]() $\mu'$
between terms, denoted by
$\mu'$
between terms, denoted by
![]() $\mu' \supseteq \mu$
, such that
$\mu' \supseteq \mu$
, such that
![]() $\mu'|_{T_1} = \mu$
. A homomorphism from a structure
$\mu'|_{T_1} = \mu$
. A homomorphism from a structure
![]() $S_1$
to a structure
$S_1$
to a structure
![]() $S_2$
is any map
$S_2$
is any map
![]() $h: \mathit{dom}(S_1) \rightarrow \mathit{dom}(S_2)$
such that both the following hold: (i) if
$h: \mathit{dom}(S_1) \rightarrow \mathit{dom}(S_2)$
such that both the following hold: (i) if
![]() $t \in \mathsf{C} \cap \mathit{dom}(S_1)$
, then
$t \in \mathsf{C} \cap \mathit{dom}(S_1)$
, then
![]() $h(t) = t$
; and (ii)
$h(t) = t$
; and (ii)
![]() $h(S_1) = \{P(h(\mathbf{t})) : P(\mathbf{t}) \in S_1\} \subseteq S_2$
.
$h(S_1) = \{P(h(\mathbf{t})) : P(\mathbf{t}) \in S_1\} \subseteq S_2$
.
2.2 Conjunctive queries
A conjunctive query (CQ) q over a schema
![]() $\mathbf{S}$
is a (first-order) formula of the form
$\mathbf{S}$
is a (first-order) formula of the form
where
![]() $\mathbf{x}$
and
$\mathbf{x}$
and
![]() $\mathbf{y}$
are tuples (often seen as sets) of variables such that
$\mathbf{y}$
are tuples (often seen as sets) of variables such that
![]() $\mathbf{x} \cap \mathbf{y} = \emptyset$
, and
$\mathbf{x} \cap \mathbf{y} = \emptyset$
, and
![]() $\Phi(\mathbf{x,y})$
is a conjunction (often seen as a set) of atoms using only predicates from
$\Phi(\mathbf{x,y})$
is a conjunction (often seen as a set) of atoms using only predicates from
![]() $\mathbf{S}$
. In particular,
$\mathbf{S}$
. In particular,
–
 $\mathit{dom}(\Phi) \subseteq \mathbf{x} \cup \mathbf{y} \cup \mathsf{C}$
,
$\mathit{dom}(\Phi) \subseteq \mathbf{x} \cup \mathbf{y} \cup \mathsf{C}$
,– whenever a variable z belongs to
 $\mathbf{x} \cup \mathbf{y}$
, then z occurs also in
$\mathbf{x} \cup \mathbf{y}$
, then z occurs also in
 $\Phi$
,
$\Phi$
,–
 $\mathbf{x}$
are the output variables of q, and
$\mathbf{x}$
are the output variables of q, and–
 $\mathbf{y}$
are the existential variables of q.
$\mathbf{y}$
are the existential variables of q.
To highlight the output variables, we may write
![]() $q(\mathbf{x})$
instead of q. The evaluation of q over an instance I is the set q(I) of every tuple
$q(\mathbf{x})$
instead of q. The evaluation of q over an instance I is the set q(I) of every tuple
![]() $\mathbf{t}$
of constants admitting a homomorphism
$\mathbf{t}$
of constants admitting a homomorphism
![]() $h_{\mathbf{t}}$
from
$h_{\mathbf{t}}$
from
![]() $\Phi(\mathbf{x,y})$
to I such that
$\Phi(\mathbf{x,y})$
to I such that
![]() $h_{\mathbf{t}}(\mathbf{x}) = \mathbf{t}$
.
$h_{\mathbf{t}}(\mathbf{x}) = \mathbf{t}$
.
A Boolean conjunctive query (BCQ) is a CQ with no output variable, namely an expression of the form
![]() $\langle \rangle \leftarrow \exists \ \mathbf{y} \ \Phi(\mathbf{y})$
. An instance I satisfies a BCQ q, denoted
$\langle \rangle \leftarrow \exists \ \mathbf{y} \ \Phi(\mathbf{y})$
. An instance I satisfies a BCQ q, denoted
![]() $I \models q$
, if q(I) is nonempty, namely q(I) contains only the empty tuple
$I \models q$
, if q(I) is nonempty, namely q(I) contains only the empty tuple
![]() $\langle \rangle $
.
$\langle \rangle $
.
2.3 Tuple-generating dependencies
A tuple-generating dependency (TGD)
![]() $\sigma$
– also known as (existential) rule – over a schema
$\sigma$
– also known as (existential) rule – over a schema
![]() $\mathbf{S}$
is a (first-order) formula of the form
$\mathbf{S}$
is a (first-order) formula of the form
where
![]() $\mathbf{x}$
,
$\mathbf{x}$
,
![]() $\mathbf{y}$
, and
$\mathbf{y}$
, and
![]() $\mathbf{z}$
are pairwise disjoint tuples of variables, and both
$\mathbf{z}$
are pairwise disjoint tuples of variables, and both
![]() $\Phi(\mathbf{x,y})$
and
$\Phi(\mathbf{x,y})$
and
![]() $\Psi(\mathbf{x,z})$
are conjunctions (often seen as a sets) of atoms using only predicates from
$\Psi(\mathbf{x,z})$
are conjunctions (often seen as a sets) of atoms using only predicates from
![]() $\mathbf{S}$
. In particular,
$\mathbf{S}$
. In particular,
–
 $\Phi$
(resp.,
$\Phi$
(resp.,
 $\Psi$
) contains all and only the variables in
$\Psi$
) contains all and only the variables in
 $\mathbf{x} \cup \mathbf{y}$
(resp.,
$\mathbf{x} \cup \mathbf{y}$
(resp.,
 $\mathbf{x} \cup \mathbf{z}$
),
$\mathbf{x} \cup \mathbf{z}$
),– constants (but not nulls) may also occur in
 $\sigma$
,
$\sigma$
,–
 $\mathbf{x} \cup \mathbf{y}$
are the universal variables of
$\mathbf{x} \cup \mathbf{y}$
are the universal variables of
 $\sigma$
denoted by
$\sigma$
denoted by
 $\mathit{vars_\forall}(\sigma)$
,
$\mathit{vars_\forall}(\sigma)$
,–
 $\mathbf{z}$
are the existential variables of
$\mathbf{z}$
are the existential variables of
 $\sigma$
denoted by
$\sigma$
denoted by
 $\mathit{vars_\exists}(\sigma)$
, and
$\mathit{vars_\exists}(\sigma)$
, and–
 $\mathbf{x}$
are the frontier variables of
$\mathbf{x}$
are the frontier variables of
 $\sigma$
denoted by
$\sigma$
denoted by
 $\mathsf{vars_\curvearrowright}(\sigma)$
.
$\mathsf{vars_\curvearrowright}(\sigma)$
.
We refer to
![]() $\mathit{body}(\sigma) = \Phi$
and
$\mathit{body}(\sigma) = \Phi$
and
![]() $\mathit{head}(\sigma) = \Psi$
as the body and head of
$\mathit{head}(\sigma) = \Psi$
as the body and head of
![]() $\sigma$
, respectively. If
$\sigma$
, respectively. If
![]() $|\mathit{head}(\sigma)| = 1$
, the TGD is called single-head, otherwise it called multi-head. If
$|\mathit{head}(\sigma)| = 1$
, the TGD is called single-head, otherwise it called multi-head. If
![]() $\mathit{vars_\exists}(\sigma) = \emptyset$
and
$\mathit{vars_\exists}(\sigma) = \emptyset$
and
![]() $|\mathit{head}(\sigma)|=1$
, then
$|\mathit{head}(\sigma)|=1$
, then
![]() $\sigma$
is called
$\sigma$
is called
![]() $\mathit{datalog}$
rule. With
$\mathit{datalog}$
rule. With
![]() $ \mathit{h}\textrm{-}\mathit{preds}(\sigma) $
(resp.,
$ \mathit{h}\textrm{-}\mathit{preds}(\sigma) $
(resp.,
![]() $\mathit{b}\textrm{-}\mathit{preds}(\sigma)$
) we denote the set of predicates in
$\mathit{b}\textrm{-}\mathit{preds}(\sigma)$
) we denote the set of predicates in
![]() $\mathit{head}(\sigma)$
(resp.,
$\mathit{head}(\sigma)$
(resp.,
![]() $\mathit{body}(\sigma)$
). An instance I satisfies
$\mathit{body}(\sigma)$
). An instance I satisfies
![]() $\sigma$
, written
$\sigma$
, written
![]() $I \models \sigma$
, if the existence of a homomorphism h from
$I \models \sigma$
, if the existence of a homomorphism h from
![]() $\Phi$
to I implies the existence of a homomorphism
$\Phi$
to I implies the existence of a homomorphism
![]() $h' \supseteq h_{| \mathbf{x}}$
from
$h' \supseteq h_{| \mathbf{x}}$
from
![]() $\Psi$
to I.
$\Psi$
to I.
An ontology
![]() $\Sigma$
is a set of rules. An instance I satisfies
$\Sigma$
is a set of rules. An instance I satisfies
![]() $\Sigma$
, written
$\Sigma$
, written
![]() $I \models \Sigma$
, if
$I \models \Sigma$
, if
![]() $I \models \sigma$
for each
$I \models \sigma$
for each
![]() $ \sigma \in \Sigma $
. Without loss of generality, we assume that
$ \sigma \in \Sigma $
. Without loss of generality, we assume that
![]() $\mathit{vars}(\sigma_1) \cap \mathit{vars}(\sigma_2)~=~\emptyset$
, for each pair
$\mathit{vars}(\sigma_1) \cap \mathit{vars}(\sigma_2)~=~\emptyset$
, for each pair
![]() $\sigma_1, \sigma_2$
of rules in
$\sigma_1, \sigma_2$
of rules in
![]() $\Sigma$
. Operators
$\Sigma$
. Operators
![]() $\mathit{vars_\exists}$
,
$\mathit{vars_\exists}$
,
![]() $\mathit{h}\textrm{-}\mathit{preds}$
, and
$\mathit{h}\textrm{-}\mathit{preds}$
, and
![]() $\mathit{b}\textrm{-}\mathit{preds}$
naturally extend on ontologies.
$\mathit{b}\textrm{-}\mathit{preds}$
naturally extend on ontologies.
A class
![]() $\mathcal{C}$
of ontologies is any (typically infinite) set of TGDs fulfilling some syntactic or semantic conditions (see, e.g., the classes shown in Table 1, some of which will be formally defined in the subsequent sections). In particular,
$\mathcal{C}$
of ontologies is any (typically infinite) set of TGDs fulfilling some syntactic or semantic conditions (see, e.g., the classes shown in Table 1, some of which will be formally defined in the subsequent sections). In particular,
![]() $\mathsf{Datalog}$
is the class of ontologies containing only datalog rules.
$\mathsf{Datalog}$
is the class of ontologies containing only datalog rules.
Finally, the schema of an ontology
![]() $\Sigma$
, denoted
$\Sigma$
, denoted
![]() $\mathit{sch}(\Sigma)$
, is the subset of
$\mathit{sch}(\Sigma)$
, is the subset of
![]() $ \mathbf{S}$
containing all and only the predicates occurring in
$ \mathbf{S}$
containing all and only the predicates occurring in
![]() $\Sigma$
, whereas
$\Sigma$
, whereas
![]() $ \mathit{arity}(\Sigma) = \max_{P \in \mathit{sch}(\Sigma)} \mathit{arity}(P)$
. For simplicity of exposition, we write
$ \mathit{arity}(\Sigma) = \max_{P \in \mathit{sch}(\Sigma)} \mathit{arity}(P)$
. For simplicity of exposition, we write
![]() $\mathit{pos}(\Sigma)$
instead of
$\mathit{pos}(\Sigma)$
instead of
![]() $\mathit{pos}(\mathit{sch}(\Sigma))$
.
$\mathit{pos}(\mathit{sch}(\Sigma))$
.
2.4 Ontological query answering
Consider a database D and a set
![]() $\Sigma$
of TGDs. A model of D and
$\Sigma$
of TGDs. A model of D and
![]() $\Sigma$
is an instance I such that
$\Sigma$
is an instance I such that
![]() $I \supseteq D$
and
$I \supseteq D$
and
![]() $I \models \Sigma$
. Let
$I \models \Sigma$
. Let
![]() $\mathit{mods}(D, \Sigma)$
be the set of all models of D and
$\mathit{mods}(D, \Sigma)$
be the set of all models of D and
![]() $\Sigma$
. The certain answers to a CQ q w.r.t. D and
$\Sigma$
. The certain answers to a CQ q w.r.t. D and
![]() $\Sigma$
are defined as the set of tuples
$\Sigma$
are defined as the set of tuples
![]() $ \mathit{cert}(q, D, \Sigma) = \bigcap_{M \in \mathit{mods}(D,\Sigma)} q(M).$
Accordingly, for any fixed schema
$ \mathit{cert}(q, D, \Sigma) = \bigcap_{M \in \mathit{mods}(D,\Sigma)} q(M).$
Accordingly, for any fixed schema
![]() $\mathbf{S}$
, two ontologies
$\mathbf{S}$
, two ontologies
![]() $\Sigma_1$
and
$\Sigma_1$
and
![]() $\Sigma_2$
over
$\Sigma_2$
over
![]() $\mathbf{S}$
are said to be
$\mathbf{S}$
are said to be
![]() $\mathbf{S}$
-equivalent (in symbols
$\mathbf{S}$
-equivalent (in symbols
![]() $\Sigma_1 \equiv_\mathbf{S} \Sigma_2$
) if, for each D and q over
$\Sigma_1 \equiv_\mathbf{S} \Sigma_2$
) if, for each D and q over
![]() $\mathbf{S}$
, it holds that
$\mathbf{S}$
, it holds that
![]() $\mathit{cert}(q,D,\Sigma_1) = \mathit{cert}(q,D,\Sigma_2).$
The pair D and
$\mathit{cert}(q,D,\Sigma_1) = \mathit{cert}(q,D,\Sigma_2).$
The pair D and
![]() $\Sigma$
satisfies a BCQ q, written
$\Sigma$
satisfies a BCQ q, written
![]() $D \cup \Sigma \models q$
, if
$D \cup \Sigma \models q$
, if
![]() $\mathit{cert}(q, D, \Sigma) = \langle \rangle$
, namely
$\mathit{cert}(q, D, \Sigma) = \langle \rangle$
, namely
![]() $M \models q$
for each
$M \models q$
for each
![]() $M \in \mathit{mods}(D,\Sigma)$
. Fix a class
$M \in \mathit{mods}(D,\Sigma)$
. Fix a class
![]() $\mathcal{C}$
of ontologies. The computational problem studied in this work – called cert-eval
$\mathcal{C}$
of ontologies. The computational problem studied in this work – called cert-eval
![]() ${{[{{\mathcal{C}}}]}}$
– can be schematized as follows:
${{[{{\mathcal{C}}}]}}$
– can be schematized as follows:

In what follows, with a slight abuse of terminology, whenever we say that
![]() ${{\mathcal{C}}}$
is decidable, we mean that cert-eval
${{\mathcal{C}}}$
is decidable, we mean that cert-eval
![]() ${{[{{\mathcal{C}}}]}}$
is decidable. Note that
${{[{{\mathcal{C}}}]}}$
is decidable. Note that
![]() $\mathbf{c} \in \mathit{cert}(q, D, \Sigma)$
if, and only if,
$\mathbf{c} \in \mathit{cert}(q, D, \Sigma)$
if, and only if,
![]() $D \cup \Sigma \models q(\mathbf{c})$
, where
$D \cup \Sigma \models q(\mathbf{c})$
, where
![]() $q(\mathbf{c})$
is the BCQ obtained from
$q(\mathbf{c})$
is the BCQ obtained from
![]() $q(\mathbf{x})$
by replacing, for each
$q(\mathbf{x})$
by replacing, for each
![]() $i \in \{1,...,|\mathbf{x}|\}$
, every occurrence of the variable
$i \in \{1,...,|\mathbf{x}|\}$
, every occurrence of the variable
![]() $\mathbf{x}[i]$
with the constant
$\mathbf{x}[i]$
with the constant
![]() $\mathbf{c}[i]$
. Actually, the former problem is
$\mathbf{c}[i]$
. Actually, the former problem is
![]() ${{{ \textbf{AC}_0}}}$
reducible to the latter.
${{{ \textbf{AC}_0}}}$
reducible to the latter.
While considering the computational complexity of cert-eval
![]() ${{[{{\mathcal{C}}}]}}$
, we recall the following convention: (i) combined complexity means that D,
${{[{{\mathcal{C}}}]}}$
, we recall the following convention: (i) combined complexity means that D,
![]() $\Sigma$
, q, and
$\Sigma$
, q, and
![]() $\mathbf{c}$
are given in input; and (ii) data complexity means that only D and
$\mathbf{c}$
are given in input; and (ii) data complexity means that only D and
![]() $\mathbf{c}$
are given in input, whereas
$\mathbf{c}$
are given in input, whereas
![]() $\Sigma$
and q are considered fixed. Accordingly, we point out that complexity results reported in Table 1 refer to cert-eval
$\Sigma$
and q are considered fixed. Accordingly, we point out that complexity results reported in Table 1 refer to cert-eval
![]() ${{[{{\mathcal{C}}}]}}$
under this convention.
${{[{{\mathcal{C}}}]}}$
under this convention.
2.5 The chase procedure
The chase procedure (Deutsch et al. 2008) is a tool exploited for reasoning with TGDs. Consider a database D and a set
![]() $\Sigma$
of TGDs. Given an instance
$\Sigma$
of TGDs. Given an instance
![]() $I \supseteq D$
, a trigger for I is any pair
$I \supseteq D$
, a trigger for I is any pair
![]() $\langle \sigma, h\rangle$
, where
$\langle \sigma, h\rangle$
, where
![]() $\sigma \in \Sigma$
is a rule as in equation (2) and h is a homomorphism from
$\sigma \in \Sigma$
is a rule as in equation (2) and h is a homomorphism from
![]() $\mathit{body}(\sigma)$
to I. Let
$\mathit{body}(\sigma)$
to I. Let
![]() $I' = I \cup h'(\mathit{head}(\sigma))$
, where
$I' = I \cup h'(\mathit{head}(\sigma))$
, where
![]() $h' \supseteq h|_{\mathbf{x}}$
maps each
$h' \supseteq h|_{\mathbf{x}}$
maps each
![]() $z \in \mathit{vars_\exists}(\sigma)$
to a “fresh” null h’(z) not occurring in I such that
$z \in \mathit{vars_\exists}(\sigma)$
to a “fresh” null h’(z) not occurring in I such that
![]() $z_1 \neq z_2$
in
$z_1 \neq z_2$
in
![]() $\mathit{vars_\exists}(\sigma)$
implies
$\mathit{vars_\exists}(\sigma)$
implies
![]() $h'(z_1) \neq h'(z_2)$
. Such an operation which constructs I’ from I is called chase step and denoted
$h'(z_1) \neq h'(z_2)$
. Such an operation which constructs I’ from I is called chase step and denoted
![]() $\langle \sigma, h \rangle (I) = I'$
.
$\langle \sigma, h \rangle (I) = I'$
.
Without loss of generality, we assume that nulls introduced at each trigger functionally depend on the pair
![]() $ \langle \sigma, h \rangle $
that is involved in the trigger. For example, given a rule
$ \langle \sigma, h \rangle $
that is involved in the trigger. For example, given a rule
![]() $\sigma$
as in equation (2) and a homomorphism h, it is sufficient to pick
$\sigma$
as in equation (2) and a homomorphism h, it is sufficient to pick
![]() $ \varphi_{\langle \mathbf{z},h(\mathbf{x},\mathbf{y}) \rangle} $
as the fresh null replacing
$ \varphi_{\langle \mathbf{z},h(\mathbf{x},\mathbf{y}) \rangle} $
as the fresh null replacing
![]() $\mathbf{z}$
when the chase produces the trigger
$\mathbf{z}$
when the chase produces the trigger
![]() $\langle \sigma, h \rangle$
. Accordingly, the processing order of rules and triggers does not change the result of the chase, and hence
$\langle \sigma, h \rangle$
. Accordingly, the processing order of rules and triggers does not change the result of the chase, and hence
![]() $\mathit{chase}(D, \Sigma$
) can be considered unique. The chase procedure of
$\mathit{chase}(D, \Sigma$
) can be considered unique. The chase procedure of
![]() $D \cup \Sigma$
is an exhaustive application of chase steps, starting from D, which produce a sequence
$D \cup \Sigma$
is an exhaustive application of chase steps, starting from D, which produce a sequence
![]() $I_0 = D \subset I_1 \subset I_2 \subset \dots \subset I_m \subset \dots$
of instances in such a way that: (i) for each
$I_0 = D \subset I_1 \subset I_2 \subset \dots \subset I_m \subset \dots$
of instances in such a way that: (i) for each
![]() $i\geq 0$
,
$i\geq 0$
,
![]() $I_{i+1} = \langle \sigma, h \rangle (I_{i})$
is a chase step obtained via some trigger
$I_{i+1} = \langle \sigma, h \rangle (I_{i})$
is a chase step obtained via some trigger
![]() $\langle \sigma, h \rangle$
for
$\langle \sigma, h \rangle$
for
![]() $I_{i}$
; (ii) for each
$I_{i}$
; (ii) for each
![]() $i \geq 0$
, if there exists a trigger
$i \geq 0$
, if there exists a trigger
![]() $\langle \sigma, h \rangle$
for
$\langle \sigma, h \rangle$
for
![]() $I_i$
, then there exists some
$I_i$
, then there exists some
![]() $j>i$
such that
$j>i$
such that
![]() $I_{j} = \langle \sigma, h\rangle (I_{j-1})$
is a chase step; and (iii) any trigger
$I_{j} = \langle \sigma, h\rangle (I_{j-1})$
is a chase step; and (iii) any trigger
![]() $\langle \sigma, h\rangle$
is used only once. We define
$\langle \sigma, h\rangle$
is used only once. We define
![]() $\mathit{chase}(D,\Sigma) = \cup_{i\geq0} I_i$
.
$\mathit{chase}(D,\Sigma) = \cup_{i\geq0} I_i$
.
The chase bottom is the finite set of all null-free atoms in
![]() $\mathit{chase}(D,\Sigma)$
and is defined as
$\mathit{chase}(D,\Sigma)$
and is defined as
![]() $\mathit{chase}^{\bot} (D, \Sigma) = \mathit{chase}(D, \Sigma) \cap {{\mathit{HB}}}(D)$
.
$\mathit{chase}^{\bot} (D, \Sigma) = \mathit{chase}(D, \Sigma) \cap {{\mathit{HB}}}(D)$
.
It is well know that
![]() $\mathit{chase}(D,\Sigma)$
is a universal model of
$\mathit{chase}(D,\Sigma)$
is a universal model of
![]() $D \cup \Sigma$
, that is, for each
$D \cup \Sigma$
, that is, for each
![]() $M \in \mathit{mods}(D, \Sigma)$
there is a homomorphism from
$M \in \mathit{mods}(D, \Sigma)$
there is a homomorphism from
![]() $\mathit{chase}(D,\Sigma)$
to M. Hence, given a BCQ q it holds that
$\mathit{chase}(D,\Sigma)$
to M. Hence, given a BCQ q it holds that
![]() $\mathit{chase}(D,\Sigma) \models q \Leftrightarrow D \cup \Sigma \models q$
.
$\mathit{chase}(D,\Sigma) \models q \Leftrightarrow D \cup \Sigma \models q$
.
We recall that
![]() $\mathit{chase}(D, \Sigma)$
can be decomposed into levels (Calì et al. Reference Calì, Gottlob and Pieris2010): each atom of D has level
$\mathit{chase}(D, \Sigma)$
can be decomposed into levels (Calì et al. Reference Calì, Gottlob and Pieris2010): each atom of D has level
![]() $\gamma = 0$
; an atom of
$\gamma = 0$
; an atom of
![]() $\mathit{chase}(D,\Sigma)$
has level
$\mathit{chase}(D,\Sigma)$
has level
![]() $\gamma + 1$
if, during its generation, the exploited trigger
$\gamma + 1$
if, during its generation, the exploited trigger
![]() $\langle \sigma, h \rangle$
maps the body of
$\langle \sigma, h \rangle$
maps the body of
![]() $\sigma$
via h to atoms whose maximum level is
$\sigma$
via h to atoms whose maximum level is
![]() $\gamma$
. We refer to the part of the chase up to level
$\gamma$
. We refer to the part of the chase up to level
![]() $\gamma$
as
$\gamma$
as
![]() $\mathit{chase}^\gamma(D, \Sigma)$
. Clearly,
$\mathit{chase}^\gamma(D, \Sigma)$
. Clearly,
![]() $\mathit{chase}(D,\Sigma) = \cup_{\gamma \geq 0} \mathit{chase}^\gamma(D, \Sigma)$
. Finally, a trigger involved at a certain level j if it gives rise to an atom of level j.
$\mathit{chase}(D,\Sigma) = \cup_{\gamma \geq 0} \mathit{chase}^\gamma(D, \Sigma)$
. Finally, a trigger involved at a certain level j if it gives rise to an atom of level j.
3 Considered decidable classes of TGDs
In this section we provide an overview of the main existing decidable classes of TGDs. We recall both syntactic and semantic classes, where the first are based on a specific syntactic condition that can be checked, while the latter are classes that do not come with a syntactic property that can be checked on rules and, hence, are not recognizable. Finally, we introduce a very simple new class of existential rules called Af-Inds. We will exploit the latter to sharpen our results presented in Sections 5 and 6.
3.1 Preliminary notions
We start fixing some basics notions. We have chosen to provide a uniform notation for the key existing notions of affected and invaded positions, such as attacked, protected, harmless, harmful, and dangerous variables (Leone et al. Reference Leone, Manna, Terracina and Veltri2019; Calì et al. Reference Calì, Gottlob and Kifer2013; Krötzsch and Rudolph 2011; Berger et al. Reference Berger, Gottlob, Pieris and Sallinger2022; Gottlob et al. 2022). Basically, these notions serve to separate positions in which the chase can introduce only constants from those where nulls might appear.
Definition 1 (S-affected positions) Consider an ontology
![]() $\Sigma$
and a variable
$\Sigma$
and a variable
![]() $ z \in \mathit{vars_\exists}(\Sigma) $
. A position
$ z \in \mathit{vars_\exists}(\Sigma) $
. A position
![]() $\pi \in \mathsf{pos}(\Sigma)$
is z-affected (or invaded by z) if one of the following two properties holds: (i) there exists
$\pi \in \mathsf{pos}(\Sigma)$
is z-affected (or invaded by z) if one of the following two properties holds: (i) there exists
![]() $ \sigma \in \Sigma $
such that z appears in the head of
$ \sigma \in \Sigma $
such that z appears in the head of
![]() $ \sigma $
at position
$ \sigma $
at position
![]() $\pi$
; (ii) there exist
$\pi$
; (ii) there exist
![]() $ \sigma \in \Sigma $
and
$ \sigma \in \Sigma $
and
![]() $ x \in \mathsf{front}(\sigma) $
such that x occurs both in
$ x \in \mathsf{front}(\sigma) $
such that x occurs both in
![]() $ \mathit{head}(\sigma) $
at position
$ \mathit{head}(\sigma) $
at position
![]() $\pi$
and in
$\pi$
and in
![]() $ \mathit{body}(\sigma) $
at z-affected positions only. Moreover, a position
$ \mathit{body}(\sigma) $
at z-affected positions only. Moreover, a position
![]() $ \pi \in \mathsf{pos}(\Sigma)$
is S - affected, where
$ \pi \in \mathsf{pos}(\Sigma)$
is S - affected, where
![]() $ S \subseteq \mathit{vars_\exists}(\Sigma) $
, if: (i) for each
$ S \subseteq \mathit{vars_\exists}(\Sigma) $
, if: (i) for each
![]() $ z \in S $
,
$ z \in S $
,
![]() $ \pi $
is z-affected; and (ii) for each
$ \pi $
is z-affected; and (ii) for each
![]() $ z \in \mathit{vars_\exists}(\Sigma) $
, if
$ z \in \mathit{vars_\exists}(\Sigma) $
, if
![]() $ \pi $
is z -affected, then
$ \pi $
is z -affected, then
![]() $ z \in S $
.
$ z \in S $
.
![]()
Note that for every position
![]() $ \pi $
there exists a unique set S such that
$ \pi $
there exists a unique set S such that
![]() $\pi$
is S-affected. We write
$\pi$
is S-affected. We write
![]() $\mathit{aff}(\pi)$
for this set S. Moreover,
$\mathit{aff}(\pi)$
for this set S. Moreover,
![]() $ \mathit{aff}(\Sigma) = \{\pi \in \mathit{pos}(\Sigma) \ | \ \mathit{aff}(\pi) \neq \emptyset \}, $
and
$ \mathit{aff}(\Sigma) = \{\pi \in \mathit{pos}(\Sigma) \ | \ \mathit{aff}(\pi) \neq \emptyset \}, $
and
![]() $ \mathit{nonaff}(\Sigma) = \mathit{pos}(\Sigma) \setminus \mathit{aff}(\Sigma).$
$ \mathit{nonaff}(\Sigma) = \mathit{pos}(\Sigma) \setminus \mathit{aff}(\Sigma).$
We point out that the notion above presented is a refined version of the classical notion of affected position (Calì et al. Reference Calì, Gottlob and Kifer2008). In particular, it holds that if a position
![]() $\pi$
is S-affected, then
$\pi$
is S-affected, then
![]() $\pi$
is also affected; whereas if
$\pi$
is also affected; whereas if
![]() $\pi$
is affected, then
$\pi$
is affected, then
![]() $\pi$
may not be S-affected. Moreover, the S-affected notion coincides with the one of attacked positions by a variable (Leone et al. Reference Leone, Manna, Terracina and Veltri2019; Krötzsch and Rudolph 2011). We highlight that its key nature and properties are not modified by the notion of S-affected position introduced above. Hence, for simplicity of exposition, we give only this refined definition. In the same spirit, we classify variables occurring in a conjunction of atoms.
$\pi$
may not be S-affected. Moreover, the S-affected notion coincides with the one of attacked positions by a variable (Leone et al. Reference Leone, Manna, Terracina and Veltri2019; Krötzsch and Rudolph 2011). We highlight that its key nature and properties are not modified by the notion of S-affected position introduced above. Hence, for simplicity of exposition, we give only this refined definition. In the same spirit, we classify variables occurring in a conjunction of atoms.
Definition 2 (Variables classification) Let
![]() $\sigma$
be a TGD and
$\sigma$
be a TGD and
![]() $ x \in \mathit{vars}(\mathit{body}(\sigma)) $
. Then, (i) if x occurs at positions
$ x \in \mathit{vars}(\mathit{body}(\sigma)) $
. Then, (i) if x occurs at positions
![]() $ \pi_1, \dots, \pi_n $
and
$ \pi_1, \dots, \pi_n $
and
![]() $ \bigcap_{i=1}^{n} \mathsf{aff}(\pi_i) = \emptyset $
, x is said to be
$ \bigcap_{i=1}^{n} \mathsf{aff}(\pi_i) = \emptyset $
, x is said to be
![]() $\mathit{harmless}$
; (ii) if x is not harmless, with
$\mathit{harmless}$
; (ii) if x is not harmless, with
![]() $S = \bigcap_{i=1}^{n} \mathsf{aff}(\pi_i) $
, it is said to be S -harmful; (iii) if x is S -harmful and belongs to
$S = \bigcap_{i=1}^{n} \mathsf{aff}(\pi_i) $
, it is said to be S -harmful; (iii) if x is S -harmful and belongs to
![]() $ \mathsf{vars_\curvearrowright}(\sigma) $
, x is S -dangerous.
$ \mathsf{vars_\curvearrowright}(\sigma) $
, x is S -dangerous.
![]()
Given a variable x that is S-dangerous, we write
![]() $ \mathit{dang}(x) $
for the set S . Hereinafter, for simplicity of exposition, the prefix S- is omitted when it is not necessary. Consider an ontology
$ \mathit{dang}(x) $
for the set S . Hereinafter, for simplicity of exposition, the prefix S- is omitted when it is not necessary. Consider an ontology
![]() $\Sigma$
. Given a rule
$\Sigma$
. Given a rule
![]() $\sigma \in \Sigma$
, we denote by
$\sigma \in \Sigma$
, we denote by
![]() $\mathit{dang}(\sigma)$
(resp.,
$\mathit{dang}(\sigma)$
(resp.,
![]() $\mathit{harmless}(\sigma)$
and
$\mathit{harmless}(\sigma)$
and
![]() $\mathit{harmful}(\sigma)$
) the dangerous (resp., harmless and harmful) variables in
$\mathit{harmful}(\sigma)$
) the dangerous (resp., harmless and harmful) variables in
![]() $\sigma$
. These sets of variables naturally extend to the whole
$\sigma$
. These sets of variables naturally extend to the whole
![]() $\Sigma$
by taking, for each of them, the union over all the rules of
$\Sigma$
by taking, for each of them, the union over all the rules of
![]() $\Sigma$
.
$\Sigma$
.
3.2 Decidable classes of existential rules
We now survey the 15 concrete classes reported in Table 1 as well as the known abstract classes based on semantic conditions. On the one side, we report some specific syntactic conditions whenever these are useful for the rest of the presentation; on the other side, for all of them (both concrete and abstract), we recall their containment relationships. For the rest of the section, fix a
![]() ${{\textsf{Datalog}^{_\exists}}}$
ontology
${{\textsf{Datalog}^{_\exists}}}$
ontology
![]() $\Sigma$
.
$\Sigma$
.
The class
![]() ${{\textsf{FES}}}$
(Baget et al. Reference Baget, Leclère, Mugnier and Salvat2009) stands for finite expansions sets, which intuitively are sets of TGDs which ensure the termination of the chase procedure. The class
${{\textsf{FES}}}$
(Baget et al. Reference Baget, Leclère, Mugnier and Salvat2009) stands for finite expansions sets, which intuitively are sets of TGDs which ensure the termination of the chase procedure. The class
![]() ${{\textsf{BTS}}}$
(Baget et al. Reference Baget, Leclère, Mugnier and Salvat2009) stands for bounded treewidth sets, which intuitively are sets of TGDs which guarantee that the (possibly infinite) instance constructed by the chase procedure has bounded treewidth. The class
${{\textsf{BTS}}}$
(Baget et al. Reference Baget, Leclère, Mugnier and Salvat2009) stands for bounded treewidth sets, which intuitively are sets of TGDs which guarantee that the (possibly infinite) instance constructed by the chase procedure has bounded treewidth. The class
![]() ${{\textsf{FUS}}}$
(Baget et al. Reference Baget, Leclère, Mugnier and Salvat2011) stands for finite unification sets, which intuitively are sets of TGDs which guarantee the termination of (resolution-based) backward chaining procedures. The class
${{\textsf{FUS}}}$
(Baget et al. Reference Baget, Leclère, Mugnier and Salvat2011) stands for finite unification sets, which intuitively are sets of TGDs which guarantee the termination of (resolution-based) backward chaining procedures. The class
![]() ${{\textsf{SPS}}}$
(Leone et al. Reference Leone, Manna, Terracina and Veltri2019) stands for strongly parsimonious sets, which intuitively are sets of TGDs which guarantee that the parsimonious chase procedure can be reapplied a number of times that is linear in the size of the query.
${{\textsf{SPS}}}$
(Leone et al. Reference Leone, Manna, Terracina and Veltri2019) stands for strongly parsimonious sets, which intuitively are sets of TGDs which guarantee that the parsimonious chase procedure can be reapplied a number of times that is linear in the size of the query.
The class
![]() ${{\textsf{Weakly-Acyclic}}}$
(Fagin et al. Reference Fagin, Kolaitis, Miller and Popa2005) is based on the acyclicity condition. To define the latter, we recall the label graph of
${{\textsf{Weakly-Acyclic}}}$
(Fagin et al. Reference Fagin, Kolaitis, Miller and Popa2005) is based on the acyclicity condition. To define the latter, we recall the label graph of
![]() $\Sigma$
,
$\Sigma$
,
![]() $G(\Sigma) = \langle N,A\rangle$
, defined as follows: (i)
$G(\Sigma) = \langle N,A\rangle$
, defined as follows: (i)
![]() $N = \cup_{P \in \mathit{sch}(\Sigma)} \mathit{pos}(P)$
; (ii)
$N = \cup_{P \in \mathit{sch}(\Sigma)} \mathit{pos}(P)$
; (ii)
![]() $(\pi_1, \pi_2, \forall) \in A$
if there are
$(\pi_1, \pi_2, \forall) \in A$
if there are
![]() $\sigma \in \Sigma$
and
$\sigma \in \Sigma$
and
![]() $x \in \mathsf{vars_\curvearrowright}(\sigma)$
such that x occurs both in
$x \in \mathsf{vars_\curvearrowright}(\sigma)$
such that x occurs both in
![]() $\mathit{body}(\sigma)$
at position
$\mathit{body}(\sigma)$
at position
![]() $\pi_1$
and in
$\pi_1$
and in
![]() $\mathit{head}(\sigma)$
at position
$\mathit{head}(\sigma)$
at position
![]() $\pi_2$
; and (iii)
$\pi_2$
; and (iii)
![]() $(\pi_1, \pi_2, \exists) \in A$
if there are
$(\pi_1, \pi_2, \exists) \in A$
if there are
![]() $\sigma \in \Sigma$
,
$\sigma \in \Sigma$
,
![]() $x \in \mathsf{vars_\curvearrowright}(\sigma)$
, and
$x \in \mathsf{vars_\curvearrowright}(\sigma)$
, and
![]() $y \in \mathit{vars_\exists}(\sigma)$
such that both x occurs in
$y \in \mathit{vars_\exists}(\sigma)$
such that both x occurs in
![]() $\mathit{body}(\sigma)$
at position
$\mathit{body}(\sigma)$
at position
![]() $\pi_1$
and y occurs in
$\pi_1$
and y occurs in
![]() $\mathit{head}(\sigma)$
at position
$\mathit{head}(\sigma)$
at position
![]() $\pi_2$
. The existential graph of
$\pi_2$
. The existential graph of
![]() $\Sigma$
is
$\Sigma$
is
![]() $G_\exists(\Sigma) = \langle N,A\rangle$
, where: (i)
$G_\exists(\Sigma) = \langle N,A\rangle$
, where: (i)
![]() $N = \cup_{\sigma \in \Sigma}\mathit{vars_\exists}(\sigma)$
; and (ii)
$N = \cup_{\sigma \in \Sigma}\mathit{vars_\exists}(\sigma)$
; and (ii)
![]() $(X,Y) \in A$
if the rule
$(X,Y) \in A$
if the rule
![]() $\sigma$
where y occurs contains a universal variable x-affected and occurring in
$\sigma$
where y occurs contains a universal variable x-affected and occurring in
![]() $\mathit{head}(\sigma)$
. Therefore,
$\mathit{head}(\sigma)$
. Therefore,
![]() $\Sigma$
belongs to
$\Sigma$
belongs to
![]() ${{\textsf{Weakly-Acyclic}}}$
(resp.,
${{\textsf{Weakly-Acyclic}}}$
(resp.,
![]() ${{\textsf{Jointly-Acyclic}}}$
) if
${{\textsf{Jointly-Acyclic}}}$
) if
![]() $G(\Sigma)$
(resp.,
$G(\Sigma)$
(resp.,
![]() $G_\exists(\Sigma)$
) has no cycle going through an
$G_\exists(\Sigma)$
) has no cycle going through an
![]() $\exists$
-arc (resp., is acyclic).
$\exists$
-arc (resp., is acyclic).
We now recall the notion of marked variable, in order to define the class
![]() ${{\textsf{Sticky}}}$
(Calì et al. Reference Calì, Gottlob and Pieris2012b). A variable x of
${{\textsf{Sticky}}}$
(Calì et al. Reference Calì, Gottlob and Pieris2012b). A variable x of
![]() $\Sigma$
is marked if (i) there is
$\Sigma$
is marked if (i) there is
![]() $\sigma \in \Sigma$
such that x occurs in
$\sigma \in \Sigma$
such that x occurs in
![]() $\mathit{body}(\sigma)$
but not in
$\mathit{body}(\sigma)$
but not in
![]() $\mathit{head}(\sigma$
); or (ii) there is
$\mathit{head}(\sigma$
); or (ii) there is
![]() $\sigma \in \Sigma$
such that x occurs in
$\sigma \in \Sigma$
such that x occurs in
![]() $\mathit{head}(\sigma)$
at position
$\mathit{head}(\sigma)$
at position
![]() $\pi$
together with some
$\pi$
together with some
![]() $\sigma' \in \Sigma$
having a marked variable in its body at position
$\sigma' \in \Sigma$
having a marked variable in its body at position
![]() $\pi$
. Accordingly, the stickiness condition states that
$\pi$
. Accordingly, the stickiness condition states that
![]() $\Sigma$
is
$\Sigma$
is
![]() ${{\textsf{Sticky}}}$
if, for each
${{\textsf{Sticky}}}$
if, for each
![]() $\sigma \in \Sigma$
, x occurs multiple times in
$\sigma \in \Sigma$
, x occurs multiple times in
![]() $\mathit{body}(\sigma)$
implies x is not marked.
$\mathit{body}(\sigma)$
implies x is not marked.
The class
![]() ${{\textsf{Linear}}}$
(Calì et al. Reference Calì, Gottlob and Lukasiewicz2012a) is based on the linearity condition: an ontology
${{\textsf{Linear}}}$
(Calì et al. Reference Calì, Gottlob and Lukasiewicz2012a) is based on the linearity condition: an ontology
![]() $\Sigma$
belongs to
$\Sigma$
belongs to
![]() ${{\textsf{Linear}}}$
if each rule contains at most one body atoms. This class generalize the class
${{\textsf{Linear}}}$
if each rule contains at most one body atoms. This class generalize the class
![]() ${{\textsf{Inclusion-Dependencies}}}$
(Abiteboul et al. Reference Abiteboul, Hull and Vianu1995; Johnson and Klug Reference Johnson and Klug1984) in which rules contain only one body atom and one head atom and the repetition of variables is not allowed neither in the body nor in the head.
${{\textsf{Inclusion-Dependencies}}}$
(Abiteboul et al. Reference Abiteboul, Hull and Vianu1995; Johnson and Klug Reference Johnson and Klug1984) in which rules contain only one body atom and one head atom and the repetition of variables is not allowed neither in the body nor in the head.
The class
![]() ${{\textsf{Guarded}}}$
(Calì et al. Reference Calì, Gottlob and Kifer2013) is based on the guardedness condition: an ontology
${{\textsf{Guarded}}}$
(Calì et al. Reference Calì, Gottlob and Kifer2013) is based on the guardedness condition: an ontology
![]() $\Sigma$
belongs to
$\Sigma$
belongs to
![]() ${{\textsf{Guarded}}}$
if for each rule
${{\textsf{Guarded}}}$
if for each rule
![]() $\sigma \in \Sigma$
there is
$\sigma \in \Sigma$
there is
![]() $\underline{a}$
in
$\underline{a}$
in
![]() $\mathit{body}(\sigma)$
such that
$\mathit{body}(\sigma)$
such that
![]() $\mathit{vars_\forall}(\sigma) = \mathit{vars}(\underline{a})$
. In similar fashion,
$\mathit{vars_\forall}(\sigma) = \mathit{vars}(\underline{a})$
. In similar fashion,
![]() $\Sigma$
belongs to
$\Sigma$
belongs to
![]() ${{\textsf{Weakly-Guarded}}}$
if, for each
${{\textsf{Weakly-Guarded}}}$
if, for each
![]() $\sigma \in \Sigma$
, there is an atom of
$\sigma \in \Sigma$
, there is an atom of
![]() $\mathit{body}(\sigma)$
containing all the affected variables of
$\mathit{body}(\sigma)$
containing all the affected variables of
![]() $\sigma$
.
$\sigma$
.
We recall the shyness condition underlying the class
![]() ${{\textsf{Shy}}}$
(Leone et al. Reference Leone, Manna, Terracina and Veltri2019). An ontology
${{\textsf{Shy}}}$
(Leone et al. Reference Leone, Manna, Terracina and Veltri2019). An ontology
![]() $\Sigma$
is
$\Sigma$
is
![]() ${{\textsf{Shy}}}$
if, for each
${{\textsf{Shy}}}$
if, for each
![]() $\sigma \in \Sigma$
the following conditions both hold: (i) if a variable x occurs in more than one body atom, then x is harmless; (ii) for every pair of distinct dangerous variable z and w in different atoms,
$\sigma \in \Sigma$
the following conditions both hold: (i) if a variable x occurs in more than one body atom, then x is harmless; (ii) for every pair of distinct dangerous variable z and w in different atoms,
![]() $ \mathit{dang}(z) \cap \mathit{dang}(w) = \emptyset$
.
$ \mathit{dang}(z) \cap \mathit{dang}(w) = \emptyset$
.
The class
![]() ${{\textsf{Ward}}}$
(Gottlob and Pieris 2015) is based on the wardedness condition:
${{\textsf{Ward}}}$
(Gottlob and Pieris 2015) is based on the wardedness condition:
![]() $\Sigma \in {{\textsf{Ward}}}$
if, for each
$\Sigma \in {{\textsf{Ward}}}$
if, for each
![]() $\sigma \in \Sigma$
, there are no dangerous variables in
$\sigma \in \Sigma$
, there are no dangerous variables in
![]() $\mathit{body}(\sigma)$
, or there exists an atom
$\mathit{body}(\sigma)$
, or there exists an atom
![]() $\underline{a} \in \mathit{body}(\sigma)$
, called a ward, such that (i) all the dangerous variables in
$\underline{a} \in \mathit{body}(\sigma)$
, called a ward, such that (i) all the dangerous variables in
![]() $\mathit{body}(\sigma)$
occur in
$\mathit{body}(\sigma)$
occur in
![]() $\underline{a}$
, and (ii) each variable of
$\underline{a}$
, and (ii) each variable of
![]() $\mathit{vars}(\underline{a}) \cap \mathit{vars}(\mathit{body}(\sigma) \setminus \{\underline{a}\})$
is harmless.
$\mathit{vars}(\underline{a}) \cap \mathit{vars}(\mathit{body}(\sigma) \setminus \{\underline{a}\})$
is harmless.
Having finished with syntactic and semantic conditions, we close the section with a proposition stating their containment relationships (Baget et al. Reference Baget, Leclère, Mugnier and Salvat2011; Krötzsch and Rudolph 2011; Leone et al. Reference Leone, Manna, Terracina and Veltri2019; Baldazzi et al. Reference Baldazzi, Bellomarini, Favorito and Sallinger2022).
Proposition 1
The following classes are pairwise uncomparable, except for:
–
 ${{\textsf{Inclusion-Dependencies}}} \subset {{\textsf{Joinless}}}$
,
${{\textsf{Inclusion-Dependencies}}} \subset {{\textsf{Joinless}}}$
,
 ${{\textsf{Inclusion-Dependencies}}} \subset {{\textsf{Linear}}}$
;
${{\textsf{Inclusion-Dependencies}}} \subset {{\textsf{Linear}}}$
;–
 ${{\textsf{Joinless}}} \subset {{\textsf{Sticky}}} \subset {{\textsf{Sticky}}}$
-
${{\textsf{Joinless}}} \subset {{\textsf{Sticky}}} \subset {{\textsf{Sticky}}}$
-
 $\mathsf{Join} \subset {{\textsf{FUS}}}$
;
$\mathsf{Join} \subset {{\textsf{FUS}}}$
;–
 ${{\textsf{Linear}}} \subset {{\textsf{Guarded}}}$
,
${{\textsf{Linear}}} \subset {{\textsf{Guarded}}}$
,
 ${{\textsf{Linear}}} \subset \mathsf{Protected}$
;
${{\textsf{Linear}}} \subset \mathsf{Protected}$
;–
 ${{\textsf{Guarded}}} \subset \mathsf{Weakly}$
-
${{\textsf{Guarded}}} \subset \mathsf{Weakly}$
-
 ${{\textsf{Guarded}}}$
,
${{\textsf{Guarded}}}$
,
 ${{\textsf{Guarded}}} \subset \mathsf{Fr}$
-Guarded;
${{\textsf{Guarded}}} \subset \mathsf{Fr}$
-Guarded;–
 $\mathsf{Weakly}$
-
$\mathsf{Weakly}$
-
 ${{\textsf{Guarded}}} \subset \mathsf{Weakly}$
-
${{\textsf{Guarded}}} \subset \mathsf{Weakly}$
-
 $\mathsf{Fr}$
-Guarded
$\mathsf{Fr}$
-Guarded
 $\subset {{\textsf{BTS}}}$
;
$\subset {{\textsf{BTS}}}$
;–
 $\mathsf{Fr}$
-Guarded
$\mathsf{Fr}$
-Guarded
 $\subset \mathsf{Weakly}$
-
$\subset \mathsf{Weakly}$
-
 $\mathsf{Fr}$
-Guarded;
$\mathsf{Fr}$
-Guarded;–
 ${{\textsf{Datalog}}} \subset \mathsf{Weakly}$
-
${{\textsf{Datalog}}} \subset \mathsf{Weakly}$
-
 ${{\textsf{Guarded}}}$
,
${{\textsf{Guarded}}}$
,
 ${{\textsf{Datalog}}} \subset \mathsf{Protected}$
,
${{\textsf{Datalog}}} \subset \mathsf{Protected}$
,
 ${{\textsf{Datalog}}} \subset {{\textsf{Weakly-Acyclic}}}$
;
${{\textsf{Datalog}}} \subset {{\textsf{Weakly-Acyclic}}}$
;–
 $\mathsf{Protected} \subset {{\textsf{Ward}}}$
,
$\mathsf{Protected} \subset {{\textsf{Ward}}}$
,
 $\mathsf{Protected} \subset {{\textsf{Shy}}} \subset {{\textsf{SPS}}}$
;
$\mathsf{Protected} \subset {{\textsf{Shy}}} \subset {{\textsf{SPS}}}$
;–
 ${{\textsf{Weakly-Acyclic}}} \subset {{\textsf{Jointly-Acyclic}}} \subset {{\textsf{FES}}}$
.
${{\textsf{Weakly-Acyclic}}} \subset {{\textsf{Jointly-Acyclic}}} \subset {{\textsf{FES}}}$
.
Throughout the remainder of the paper, let
![]() $\mathbb{E}_{syn}$
denote the set of all 15 decidable syntactic classes reported in Table 1. Analogously, let
$\mathbb{E}_{syn}$
denote the set of all 15 decidable syntactic classes reported in Table 1. Analogously, let
![]() $\mathbb{E}_{sem}$
denote the set of known decidable abstract classes considered in this paper, namely
$\mathbb{E}_{sem}$
denote the set of known decidable abstract classes considered in this paper, namely
![]() ${{\textsf{FES}}}$
,
${{\textsf{FES}}}$
,
![]() ${{\textsf{FUS}}}$
,
${{\textsf{FUS}}}$
,
![]() ${{\textsf{BTS}}}$
, and
${{\textsf{BTS}}}$
, and
![]() ${{\textsf{SPS}}}$
.
${{\textsf{SPS}}}$
.
3.3 Autonomous full inclusion dependencies
The aim of this section is to introduce a very simple new class of existential rules called
![]() ${{\textsf{Af-Inds}}}$
. Additionally, we characterize the main properties of this class.
${{\textsf{Af-Inds}}}$
. Additionally, we characterize the main properties of this class.
Definition 3 (Inds) An ontology
![]() $\Sigma$
belongs to
$\Sigma$
belongs to
![]() ${{\textsf{Af-Inds}}}$
(autonomous full inclusion dependencies) if
${{\textsf{Af-Inds}}}$
(autonomous full inclusion dependencies) if
![]() $\Sigma$
belongs to
$\Sigma$
belongs to
![]() ${{\textsf{Inclusion-Dependencies}}}$
and the following conditions are also satisfied: (1) head predicates do not appear in bodies (autonomous property); (2) rules have no existential variables (full property).
${{\textsf{Inclusion-Dependencies}}}$
and the following conditions are also satisfied: (1) head predicates do not appear in bodies (autonomous property); (2) rules have no existential variables (full property).
Now, we show that any class
![]() ${{\mathcal{C}}}$
of TGDs in
${{\mathcal{C}}}$
of TGDs in
![]() $\mathbb{E}_{syn} \cup \mathbb{E}_{sem}$
includes the class just defined. Formally, it holds the following.
$\mathbb{E}_{syn} \cup \mathbb{E}_{sem}$
includes the class just defined. Formally, it holds the following.
Proposition 2 Consider a class
![]() ${{\mathcal{C}}} \in \mathbb{E}_{syn} \cup \mathbb{E}_{sem}$
of TGDs. Then,
${{\mathcal{C}}} \in \mathbb{E}_{syn} \cup \mathbb{E}_{sem}$
of TGDs. Then,
![]() ${{\textsf{Af-Inds}}} \subseteq {{\mathcal{C}}}$
.
${{\textsf{Af-Inds}}} \subseteq {{\mathcal{C}}}$
.
Proof. Thanks to Proposition 1, the statement becomes equivalent to show that (i)
![]() ${{\textsf{Af-Inds}}} \subseteq {{\textsf{Inclusion-Dependencies}}}$
and (ii)
${{\textsf{Af-Inds}}} \subseteq {{\textsf{Inclusion-Dependencies}}}$
and (ii)
![]() ${{\textsf{Af-Inds}}} \subseteq {{\textsf{Datalog}}}$
. By Definition 3, the class
${{\textsf{Af-Inds}}} \subseteq {{\textsf{Datalog}}}$
. By Definition 3, the class
![]() ${{\textsf{Af-Inds}}}$
contains all the rules that have only one body and head atom, without repetition of variables neither in the body nor in the head, and that satisfy the autonomous property (head atom does not appear in bodies) and the full property (rules have only one head atom without existential variables). Accordingly, relation (i) and (ii) are trivially fulfilled.
${{\textsf{Af-Inds}}}$
contains all the rules that have only one body and head atom, without repetition of variables neither in the body nor in the head, and that satisfy the autonomous property (head atom does not appear in bodies) and the full property (rules have only one head atom without existential variables). Accordingly, relation (i) and (ii) are trivially fulfilled.
We conclude the section by providing the complexity of the class Af-Inds.
Proposition 3
![]() ${{cert-eval}}[{{\textsf{Af-Inds}}}]$
is in
${{cert-eval}}[{{\textsf{Af-Inds}}}]$
is in
![]() ${{{ \textbf{AC}_0}}}$
in data complexity and
${{{ \textbf{AC}_0}}}$
in data complexity and
![]() ${{{ \textbf{NP}}{\textrm{-complete}}}}$
in combined complexity.
${{{ \textbf{NP}}{\textrm{-complete}}}}$
in combined complexity.
Proof. By Proposition 2,
![]() ${{\textsf{Af-Inds}}} \subseteq {{\textsf{Inclusion-Dependencies}}}$
. Hence, the data complexity of the problem
${{\textsf{Af-Inds}}} \subseteq {{\textsf{Inclusion-Dependencies}}}$
. Hence, the data complexity of the problem
![]() ${{cert-eval}}[{{\textsf{Af-Inds}}}]$
is inherit from that of
${{cert-eval}}[{{\textsf{Af-Inds}}}]$
is inherit from that of
![]() ${{cert-eval}}[{{\textsf{Inclusion-Dependencies}}}]$
, that is
${{cert-eval}}[{{\textsf{Inclusion-Dependencies}}}]$
, that is
![]() ${{{ \textbf{AC}_0}}}$
. For the combined complexity, we first observe that the problem
${{{ \textbf{AC}_0}}}$
. For the combined complexity, we first observe that the problem
![]() ${{cert-eval}}[{{\textsf{Af-Inds}}}]$
is
${{cert-eval}}[{{\textsf{Af-Inds}}}]$
is
![]() ${{{ \textbf{NP}}{\textrm{-hard}}}}$
, building upon the well-known fact that
${{{ \textbf{NP}}{\textrm{-hard}}}}$
, building upon the well-known fact that
![]() ${{cert-eval}}[\emptyset]$
is already
${{cert-eval}}[\emptyset]$
is already
![]() ${{{ \textbf{NP}}{\textrm{-hard}}}}$
. The latter refers to the problem of evaluating a query against a database in the absence of an ontology. Secondly, to prove the completeness of the
${{{ \textbf{NP}}{\textrm{-hard}}}}$
. The latter refers to the problem of evaluating a query against a database in the absence of an ontology. Secondly, to prove the completeness of the
![]() ${{cert-eval}}[{{\textsf{Af-Inds}}}]$
problem, we show that given a query
${{cert-eval}}[{{\textsf{Af-Inds}}}]$
problem, we show that given a query
![]() $q(\mathbf{x})$
and an ontology
$q(\mathbf{x})$
and an ontology
![]() $\Sigma$
, it is possible to construct in
$\Sigma$
, it is possible to construct in
![]() ${ \textbf{NP}}$
a CQ
${ \textbf{NP}}$
a CQ
![]() $q_\Sigma(\mathbf{x})$
such that
$q_\Sigma(\mathbf{x})$
such that
![]() $c \in cert(D,\Sigma,q)$
iff
$c \in cert(D,\Sigma,q)$
iff
![]() $c \in q_\Sigma(D)$
, with
$c \in q_\Sigma(D)$
, with
![]() $\mathbf{c}$
being a tuple in
$\mathbf{c}$
being a tuple in
![]() $\mathsf{C}^{|\mathbf{x}|}$
. To this aim, for each atom
$\mathsf{C}^{|\mathbf{x}|}$
. To this aim, for each atom
![]() $\underline{a} \in q(\mathbf{x})$
, we guess if leave
$\underline{a} \in q(\mathbf{x})$
, we guess if leave
![]() $\underline{a}$
unchanged, or “resolv"
$\underline{a}$
unchanged, or “resolv"
![]() $\underline{a}$
with the body of some rule
$\underline{a}$
with the body of some rule
![]() $\sigma$
in
$\sigma$
in
![]() $\Sigma$
such that
$\Sigma$
such that
![]() $\mathit{head}(\sigma)$
unify with
$\mathit{head}(\sigma)$
unify with
![]() $\underline{a}$
. Accordingly,
$\underline{a}$
. Accordingly,
![]() $q_\Sigma(D)$
is polynomial with respect to the input and, finally, it is possible to guess in
$q_\Sigma(D)$
is polynomial with respect to the input and, finally, it is possible to guess in
![]() ${ \textbf{NP}}$
an homomorphism to check if
${ \textbf{NP}}$
an homomorphism to check if
![]() $c \in q_\Sigma(D)$
.
$c \in q_\Sigma(D)$
.
4 Dyadic pairs of TGDs
In this section we lay the groundwork for the main contribution of the paper, that is the definition of a new decidable class of TGDs called
![]() ${{\textsf{Dyadic-}\mathcal{C}}}$
. To this aim we first introduce some preliminary notions in order to define a dyadic pair and, then we conclude with some computational properties.
${{\textsf{Dyadic-}\mathcal{C}}}$
. To this aim we first introduce some preliminary notions in order to define a dyadic pair and, then we conclude with some computational properties.
4.1 Formal definition
We start introducing the concept of head-ground set of rules, being roughly “non-recursive” rules in which nulls are neither created nor propagated.
Definition 4 (Head-ground rules) Consider an ontology
![]() $ \Sigma $
. A set
$ \Sigma $
. A set
![]() $\Sigma' \subseteq \Sigma $
is head-ground w.r.t.
$\Sigma' \subseteq \Sigma $
is head-ground w.r.t.
![]() $ \Sigma $
if the following are true: (1)
$ \Sigma $
if the following are true: (1)
![]() $ \Sigma' \in \mathsf{Datalog}$
; (2) each head atom of
$ \Sigma' \in \mathsf{Datalog}$
; (2) each head atom of
![]() $ \Sigma'$
contains only harmless variables w.r.t.
$ \Sigma'$
contains only harmless variables w.r.t.
![]() $ \Sigma$
; (3)
$ \Sigma$
; (3)
![]() $ \mathit{h}\textrm{-}\mathit{preds}(\Sigma') \cap \mathit{b}\textrm{-}\mathit{preds}(\Sigma') = \emptyset $
; and (4)
$ \mathit{h}\textrm{-}\mathit{preds}(\Sigma') \cap \mathit{b}\textrm{-}\mathit{preds}(\Sigma') = \emptyset $
; and (4)
![]() $ \mathit{h}\textrm{-}\mathit{preds}(\Sigma') \cap \mathit{h}\textrm{-}\mathit{preds}(\Sigma \setminus \Sigma') = \emptyset $
.
$ \mathit{h}\textrm{-}\mathit{preds}(\Sigma') \cap \mathit{h}\textrm{-}\mathit{preds}(\Sigma \setminus \Sigma') = \emptyset $
.
![]()
The following example is given to better understand the above definition.
Example 1 Consider the next set of rules:
 $$\begin{array}{rrcl} \sigma_1: & R(x_1, y_1), {S(y_1,u_1), T(u_1,v_1)} & \rightarrow & \exists \ z_1, w_1 \ Q(z_1, w_1)\\ \sigma_2: & C(y_2), R(x_2, z_2) & \rightarrow & S(y_2, z_2) \\ \sigma_3: & D(y_3,z_3), R(x_3, w_3) & \rightarrow & T(x_3, y_3)\end{array}$$
$$\begin{array}{rrcl} \sigma_1: & R(x_1, y_1), {S(y_1,u_1), T(u_1,v_1)} & \rightarrow & \exists \ z_1, w_1 \ Q(z_1, w_1)\\ \sigma_2: & C(y_2), R(x_2, z_2) & \rightarrow & S(y_2, z_2) \\ \sigma_3: & D(y_3,z_3), R(x_3, w_3) & \rightarrow & T(x_3, y_3)\end{array}$$
A subset of head-ground rule w.r.t.
![]() $\Sigma$
is given by
$\Sigma$
is given by
![]() $ \Sigma_\mathrm{HG} = \{ \sigma_2, \sigma_3 \}$
. In fact,
$ \Sigma_\mathrm{HG} = \{ \sigma_2, \sigma_3 \}$
. In fact,
![]() $\mathit{harmless}(\Sigma)$
is the set
$\mathit{harmless}(\Sigma)$
is the set
![]() $\{x_1, y_1, y_2, x_2, z_2, x_3,y_3, z_3, y_5, z_5\}$
; hence, according to Definition 4, it is easy to check that (i)
$\{x_1, y_1, y_2, x_2, z_2, x_3,y_3, z_3, y_5, z_5\}$
; hence, according to Definition 4, it is easy to check that (i)
![]() $\sigma_2$
and
$\sigma_2$
and
![]() $\sigma_3$
are datalog rules; (ii) the head atoms of
$\sigma_3$
are datalog rules; (ii) the head atoms of
![]() $\sigma_2$
and
$\sigma_2$
and
![]() $\sigma_3$
contain only harmless variables; (iii) both predicates S and T do not occur in the body of any rule in
$\sigma_3$
contain only harmless variables; (iii) both predicates S and T do not occur in the body of any rule in
![]() $\Sigma_\mathrm{HG}$
, and (iv) both predicates S and T do not occur in the head of any rule in
$\Sigma_\mathrm{HG}$
, and (iv) both predicates S and T do not occur in the head of any rule in
![]() $\{\sigma_1, \sigma_4, \sigma_5\}$
. On the contrary, none of the rules in
$\{\sigma_1, \sigma_4, \sigma_5\}$
. On the contrary, none of the rules in
![]() $\{\sigma_1, \sigma_4, \sigma_5\}$
can be part of any head-ground subset of
$\{\sigma_1, \sigma_4, \sigma_5\}$
can be part of any head-ground subset of
![]() $\Sigma$
. Indeed, according to Definition 4, both
$\Sigma$
. Indeed, according to Definition 4, both
![]() $\sigma_1$
and
$\sigma_1$
and
![]() $\sigma_2$
violate properties (1) and (2), whereas
$\sigma_2$
violate properties (1) and (2), whereas
![]() $\sigma_5$
violates property (2). Hence, we observe that the set
$\sigma_5$
violates property (2). Hence, we observe that the set
![]() $\Sigma_\mathrm{HG}$
is also maximal.
$\Sigma_\mathrm{HG}$
is also maximal.
![]()
Having in mind the notion of head-ground set of rules, we can now formally define what is a dyadic pair.
Definition 5 (Dyadic pairs) Consider a class
![]() ${{\mathcal{C}}}$
of TGDs. A pair
${{\mathcal{C}}}$
of TGDs. A pair
![]() $\Pi = (\Sigma_\mathrm{HG}, \Sigma_\mathcal{C}) $
of TGDs is dyadic with respect to
$\Pi = (\Sigma_\mathrm{HG}, \Sigma_\mathcal{C}) $
of TGDs is dyadic with respect to
![]() $\mathcal{C}$
if the next hold: (1)
$\mathcal{C}$
if the next hold: (1)
![]() $ \Sigma_\mathrm{HG} $
is head-ground with respect to
$ \Sigma_\mathrm{HG} $
is head-ground with respect to
![]() $ \Sigma_\mathrm{HG} \cup \Sigma_\mathcal{C}$
; and (2)
$ \Sigma_\mathrm{HG} \cup \Sigma_\mathcal{C}$
; and (2)
![]() $\Sigma_\mathcal{C} \in \mathcal{C}$
.
$\Sigma_\mathcal{C} \in \mathcal{C}$
.
![]()
Whenever the above definition applies, we also say, for short, that
![]() $\Pi$
is a
$\Pi$
is a
![]() ${{\mathcal{C}}}$
-dyadic pair. Consider the following example to more easily understand the concept of dyadic pair.
${{\mathcal{C}}}$
-dyadic pair. Consider the following example to more easily understand the concept of dyadic pair.
Example 2 Consider the following pair
![]() $\Pi = (\Sigma_\mathrm{HG}, \Sigma_\mathcal{C}) $
of TGDs, where
$\Pi = (\Sigma_\mathrm{HG}, \Sigma_\mathcal{C}) $
of TGDs, where
![]() $\Sigma_\mathrm{HG}$
is:
$\Sigma_\mathrm{HG}$
is:
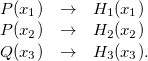 $\begin{array}{rcl} P(x_1) & \rightarrow & H_1(x_1)\\ P(x_2) & \rightarrow & H_2(x_2)\\ Q(x_3) & \rightarrow & H_3(x_3).\\ \end{array}$
$\begin{array}{rcl} P(x_1) & \rightarrow & H_1(x_1)\\ P(x_2) & \rightarrow & H_2(x_2)\\ Q(x_3) & \rightarrow & H_3(x_3).\\ \end{array}$
and
![]() $\Sigma_\mathcal{C}$
is:
$\Sigma_\mathcal{C}$
is:

In particular,
![]() $\Pi$
is a dyadic pair with respect to any
$\Pi$
is a dyadic pair with respect to any
![]() ${{\mathcal{C}}} \in \{{{\textsf{Guarded}}}, {{\textsf{Shy}}}, {{\textsf{Ward}}}.\}$
. To this aim, let
${{\mathcal{C}}} \in \{{{\textsf{Guarded}}}, {{\textsf{Shy}}}, {{\textsf{Ward}}}.\}$
. To this aim, let
![]() $\Sigma = \Sigma_\mathrm{HG} \cup \Sigma_\mathcal{C}$
. It easy computable that
$\Sigma = \Sigma_\mathrm{HG} \cup \Sigma_\mathcal{C}$
. It easy computable that
![]() $\mathit{aff}(\Sigma) = \{R[1],R[2],Q[1],S[1]\}$
, where
$\mathit{aff}(\Sigma) = \{R[1],R[2],Q[1],S[1]\}$
, where
![]() $\mathit{aff}(R[1])=\{y_1\}$
,
$\mathit{aff}(R[1])=\{y_1\}$
,
![]() $\mathit{aff}(R[2])=\{z_1\}$
,
$\mathit{aff}(R[2])=\{z_1\}$
,
![]() $\mathit{aff}(Q[1])=\{y_2\}$
, and
$\mathit{aff}(Q[1])=\{y_2\}$
, and
![]() $\mathit{aff}(S[1])=\{y_1\}$
. Accordingly,
$\mathit{aff}(S[1])=\{y_1\}$
. Accordingly,
![]() $\mathit{harmless}(\Sigma) = \{x_1,x_2,x_3\}$
,
$\mathit{harmless}(\Sigma) = \{x_1,x_2,x_3\}$
,
![]() $\mathit{harmful}(\Sigma) = \{y_3\}$
and
$\mathit{harmful}(\Sigma) = \{y_3\}$
and
![]() $ \mathit{dang}(\Sigma) = \{y_3\}$
. To prove that
$ \mathit{dang}(\Sigma) = \{y_3\}$
. To prove that
![]() $\Pi$
is a dyadic pair, we have first to show that
$\Pi$
is a dyadic pair, we have first to show that
![]() $\Sigma_\mathrm{HG}$
is an head-ground set of rules with respect to
$\Sigma_\mathrm{HG}$
is an head-ground set of rules with respect to
![]() $\Sigma$
. Clearly,
$\Sigma$
. Clearly,
![]() $\Sigma_\mathrm{HG} \in {{\textsf{Datalog}}}$
and each head atom contains only harmless variables; moreover, the head predicates do not appear neither in body atoms of
$\Sigma_\mathrm{HG} \in {{\textsf{Datalog}}}$
and each head atom contains only harmless variables; moreover, the head predicates do not appear neither in body atoms of
![]() $\Sigma_\mathrm{HG}$
nor in head atoms of
$\Sigma_\mathrm{HG}$
nor in head atoms of
![]() $\Sigma_\mathcal{C}$
. Hence,
$\Sigma_\mathcal{C}$
. Hence,
![]() $\Sigma_\mathrm{HG}$
is head-ground with respect to
$\Sigma_\mathrm{HG}$
is head-ground with respect to
![]() $\Sigma$
. It remains to show that
$\Sigma$
. It remains to show that
![]() $\Sigma_\mathcal{C} \in {{\mathcal{C}}}$
. We focus on the last rule of
$\Sigma_\mathcal{C} \in {{\mathcal{C}}}$
. We focus on the last rule of
![]() $\Sigma_\mathcal{C}$
, since the first two rules are linear rules, and hence are trivially guarded, shy and ward rules. The last rule belongs to
$\Sigma_\mathcal{C}$
, since the first two rules are linear rules, and hence are trivially guarded, shy and ward rules. The last rule belongs to
![]() ${{\textsf{Guarded}}}$
since the atom
${{\textsf{Guarded}}}$
since the atom
![]() $R(y_3,x_3)$
contains all the universal variables of the rule (guardedness condition); it belong to
$R(y_3,x_3)$
contains all the universal variables of the rule (guardedness condition); it belong to
![]() ${{\textsf{Shy}}}$
since the variable
${{\textsf{Shy}}}$
since the variable
![]() $x_3$
that occurs in two body atoms is harmless (shyness condition); finally, it belongs to
$x_3$
that occurs in two body atoms is harmless (shyness condition); finally, it belongs to
![]() ${{\textsf{Ward}}}$
since atom
${{\textsf{Ward}}}$
since atom
![]() $R(y_3,x_3)$
is the ward that contains the dangerous variables
$R(y_3,x_3)$
is the ward that contains the dangerous variables
![]() $(y_3)$
and shares with the rest of the body only harmless variables
$(y_3)$
and shares with the rest of the body only harmless variables
![]() $(x_3)$
(wardedness condition).
$(x_3)$
(wardedness condition).
![]()
The next step is to extend the query answering problem – classically defined over an ontology – over a dyadic pair. Therefore, we extend both notions of chase and certain answers for a dyadic pair. Accordingly, given a dyadic pair
![]() $\Pi = (\Sigma_\mathrm{HG}, \Sigma_\mathcal{C})$
, we define
$\Pi = (\Sigma_\mathrm{HG}, \Sigma_\mathcal{C})$
, we define
and
Now we can fix the problem studied in the rest of the paper.

4.2 Computational properties
For the rest of the section, fix a decidable class
![]() ${{\mathcal{C}}}$
of TGDs. Given a database D and a
${{\mathcal{C}}}$
of TGDs. Given a database D and a
![]() ${{\mathcal{C}}}$
-dyadic pair
${{\mathcal{C}}}$
-dyadic pair
![]() $\Pi$
of TGDs, we define the following set of ground atoms:
$\Pi$
of TGDs, we define the following set of ground atoms:
Our idea is to reduce query answering over a dyadic pair
![]() $\Pi$
to query answering over
$\Pi$
to query answering over
![]() $\mathcal{C}$
, the latter being decidable by assumption.
$\mathcal{C}$
, the latter being decidable by assumption.
Theorem 1 Consider a database D, a
![]() ${{\mathcal{C}}}$
-dyadic pair
${{\mathcal{C}}}$
-dyadic pair
![]() $\Pi = (\Sigma_\mathrm{HG},\Sigma_\mathcal{C})$
of TGDs, and a conjunctive query
$\Pi = (\Sigma_\mathrm{HG},\Sigma_\mathcal{C})$
of TGDs, and a conjunctive query
![]() $q(\mathbf{x})$
. Let
$q(\mathbf{x})$
. Let
![]() $D^+ = D \cup {{\mathit{gra}}}(D,\Pi)$
. It holds that
$D^+ = D \cup {{\mathit{gra}}}(D,\Pi)$
. It holds that
![]() ${{\mathit{dp}\textrm{-}\mathit{cert}}}(q,D, \Pi) = \mathit{cert}(q,D^+,\Sigma_\mathcal{C})$
.
${{\mathit{dp}\textrm{-}\mathit{cert}}}(q,D, \Pi) = \mathit{cert}(q,D^+,\Sigma_\mathcal{C})$
.
Proof. Consider
![]() $\Pi = (\Sigma_\mathrm{HG},\Sigma_\mathcal{C})$
. By equation (4),
$\Pi = (\Sigma_\mathrm{HG},\Sigma_\mathcal{C})$
. By equation (4),
![]() ${{\mathit{dp}\textrm{-}\mathit{cert}}}(q,D,\Pi) = \mathit{cert}(q,D,\Sigma_\mathrm{HG} \cup \Sigma_\mathcal{C})$
. Moreover, by fixing any arbitrary
${{\mathit{dp}\textrm{-}\mathit{cert}}}(q,D,\Pi) = \mathit{cert}(q,D,\Sigma_\mathrm{HG} \cup \Sigma_\mathcal{C})$
. Moreover, by fixing any arbitrary
![]() $|{\bf x}|$
-ary tuple c of constants, it holds that
$|{\bf x}|$
-ary tuple c of constants, it holds that
![]() ${\bf c} \in \mathit{cert}(q,D,\Sigma_\mathrm{HG} \cup \Sigma_\mathcal{C}) \Leftrightarrow D \cup \Sigma_\mathrm{HG} \cup \Sigma_\mathcal{C} \models q({\bf c})$
and
${\bf c} \in \mathit{cert}(q,D,\Sigma_\mathrm{HG} \cup \Sigma_\mathcal{C}) \Leftrightarrow D \cup \Sigma_\mathrm{HG} \cup \Sigma_\mathcal{C} \models q({\bf c})$
and
![]() ${\bf c} \in \mathit{cert}(q,D^+,\Sigma_\mathcal{C}) \Leftrightarrow D^+ \cup \Sigma_\mathcal{C} \models q({\bf c})$
. Let
${\bf c} \in \mathit{cert}(q,D^+,\Sigma_\mathcal{C}) \Leftrightarrow D^+ \cup \Sigma_\mathcal{C} \models q({\bf c})$
. Let
![]() $q' = q({\bf c})$
. Accordingly, the thesis boils down to showing that
$q' = q({\bf c})$
. Accordingly, the thesis boils down to showing that
![]() $[\Rightarrow]$
Assume that
$[\Rightarrow]$
Assume that
![]() $D \cup \Sigma_\mathrm{HG} \cup \Sigma_\mathcal{C} \models q'$
holds. Hence,
$D \cup \Sigma_\mathrm{HG} \cup \Sigma_\mathcal{C} \models q'$
holds. Hence,
![]() $\mathit{chase}(D , \Sigma_\mathrm{HG} \cup \Sigma_\mathcal{C}) \models q'$
. Given that
$\mathit{chase}(D , \Sigma_\mathrm{HG} \cup \Sigma_\mathcal{C}) \models q'$
. Given that
![]() ${{\mathit{gra}}}(D,\Pi) \subseteq \mathit{chase}(D, \Sigma_\mathrm{HG} \cup \Sigma_\mathcal{C})$
, it holds that
${{\mathit{gra}}}(D,\Pi) \subseteq \mathit{chase}(D, \Sigma_\mathrm{HG} \cup \Sigma_\mathcal{C})$
, it holds that
![]() $\mathit{chase}(D \cup {{\mathit{gra}}}(D,\Pi) , \Sigma_\mathrm{HG} \cup \Sigma_\mathcal{C}) \models q'$
. Moreover, since
$\mathit{chase}(D \cup {{\mathit{gra}}}(D,\Pi) , \Sigma_\mathrm{HG} \cup \Sigma_\mathcal{C}) \models q'$
. Moreover, since
![]() ${{\mathit{gra}}}(D,\Pi)$
contains all the auxiliary ground consequences of
${{\mathit{gra}}}(D,\Pi)$
contains all the auxiliary ground consequences of
![]() $\Sigma_\mathrm{HG}$
, the latter becomes equivalent to
$\Sigma_\mathrm{HG}$
, the latter becomes equivalent to
![]() $\mathit{chase}(D \cup {{\mathit{gra}}}(D,\Pi) , \Sigma_\mathcal{C}) \models q'$
. Hence,
$\mathit{chase}(D \cup {{\mathit{gra}}}(D,\Pi) , \Sigma_\mathcal{C}) \models q'$
. Hence,
![]() $D \cup {{\mathit{gra}}}(D,\Pi) \cup \Sigma_\mathcal{C} \models q'$
, that is
$D \cup {{\mathit{gra}}}(D,\Pi) \cup \Sigma_\mathcal{C} \models q'$
, that is
![]() $D^+ \cup \Sigma_\mathcal{C} \models q'$
.
$D^+ \cup \Sigma_\mathcal{C} \models q'$
.
![]() $[\Leftarrow]$
Assume that
$[\Leftarrow]$
Assume that
![]() $D^+ \cup \Sigma_\mathcal{C} \models q'$
, hence
$D^+ \cup \Sigma_\mathcal{C} \models q'$
, hence
![]() $\mathit{chase}(D^+ , \Sigma_\mathcal{C}) \models q'$
. Since
$\mathit{chase}(D^+ , \Sigma_\mathcal{C}) \models q'$
. Since
![]() $\Sigma_\mathcal{C} \subseteq \Sigma_\mathrm{HG} \cup \Sigma_\mathcal{C}$
, it holds that
$\Sigma_\mathcal{C} \subseteq \Sigma_\mathrm{HG} \cup \Sigma_\mathcal{C}$
, it holds that
![]() $\mathit{chase}(D^+, \Sigma_\mathrm{HG} \cup \Sigma_\mathcal{C}) \models q'$
. By hypothesis,
$\mathit{chase}(D^+, \Sigma_\mathrm{HG} \cup \Sigma_\mathcal{C}) \models q'$
. By hypothesis,
![]() ${{\mathit{gra}}}(D,\Pi) \subseteq \mathit{chase}(D , \Sigma_\mathrm{HG} \cup \Sigma_\mathcal{C})$
; hence
${{\mathit{gra}}}(D,\Pi) \subseteq \mathit{chase}(D , \Sigma_\mathrm{HG} \cup \Sigma_\mathcal{C})$
; hence
![]() $\mathit{chase}(D , \Sigma_\mathrm{HG} \cup \Sigma_\mathcal{C}) \models q'$
, that is
$\mathit{chase}(D , \Sigma_\mathrm{HG} \cup \Sigma_\mathcal{C}) \models q'$
, that is
![]() $D \cup \Sigma_\mathrm{HG} \cup \Sigma_\mathcal{C} \models q'$
.
$D \cup \Sigma_\mathrm{HG} \cup \Sigma_\mathcal{C} \models q'$
.
According to Theorem 1, to solve dp-cert-eval
![]() $[\mathcal{C}]$
one can first “complete” D and then performing classical query evaluation. To this aim we design Algorithms 1 and 2. The correctness of the latter will be proved in Proposition 4. Consequently, the correctness of the former is guaranteed by Theorem 1.
$[\mathcal{C}]$
one can first “complete” D and then performing classical query evaluation. To this aim we design Algorithms 1 and 2. The correctness of the latter will be proved in Proposition 4. Consequently, the correctness of the former is guaranteed by Theorem 1.
In particular, given a database D and a dyadic pair
![]() $\Pi = (\Sigma_\mathrm{HG}, \Sigma_\mathcal{C})$
, Algorithm 2 iteratively constructs the set
$\Pi = (\Sigma_\mathrm{HG}, \Sigma_\mathcal{C})$
, Algorithm 2 iteratively constructs the set
![]() $D^+ = D \cup {{\mathit{gra}}}(D,\Pi)$
, with
$D^+ = D \cup {{\mathit{gra}}}(D,\Pi)$
, with
![]() ${{\mathit{gra}}}(D,\Pi)$
being the set defined by equation (5). Roughly speaking, the first two instructions are required, respectively, to add D to
${{\mathit{gra}}}(D,\Pi)$
being the set defined by equation (5). Roughly speaking, the first two instructions are required, respectively, to add D to
![]() $D^+$
and to initialize a temporary set
$D^+$
and to initialize a temporary set
![]() $\tilde{D}$
used to store ground consequences derived from
$\tilde{D}$
used to store ground consequences derived from
![]() $\Sigma_\mathrm{HG}$
. The rest of the algorithm is an iterative procedure that computes the certain answers (instruction 5) to the queries constructed from the rules of
$\Sigma_\mathrm{HG}$
. The rest of the algorithm is an iterative procedure that computes the certain answers (instruction 5) to the queries constructed from the rules of
![]() $\Sigma_\mathrm{HG}$
(instruction 4) and completes the initial database D (instruction 7) until no more auxiliary ground atoms can be produced (instruction 6). We point out that, in general,
$\Sigma_\mathrm{HG}$
(instruction 4) and completes the initial database D (instruction 7) until no more auxiliary ground atoms can be produced (instruction 6). We point out that, in general,
![]() $\tilde{D} \subseteq {{\mathit{gra}}}(D,\Pi)$
holds; in particular,
$\tilde{D} \subseteq {{\mathit{gra}}}(D,\Pi)$
holds; in particular,
![]() $\tilde{D} = {{\mathit{gra}}}(D,\Pi)$
holds in the last execution of instruction 7 or, equivalently, when the condition
$\tilde{D} = {{\mathit{gra}}}(D,\Pi)$
holds in the last execution of instruction 7 or, equivalently, when the condition
![]() $D \cup \tilde{D} \supset D^+$
examined at instruction 6 is false, since all the auxiliary ground atoms have been added to
$D \cup \tilde{D} \supset D^+$
examined at instruction 6 is false, since all the auxiliary ground atoms have been added to
![]() $D^+$
.
$D^+$
.
Algorithm 1: DpCertEval[![]() $\mathcal{C}$](q, D, Π, c)
$\mathcal{C}$](q, D, Π, c)

Before we prove that Algorithm 2 always terminates and correctly constructs
![]() $D^+$
, we show the following preliminary lemma.
$D^+$
, we show the following preliminary lemma.
Algorithm 2: Complete[![]() $_\mathcal{C}$](D, Π)
$_\mathcal{C}$](D, Π)

Lemma 1 Consider a database D and a set
![]() $\Sigma$
of TGDs. Let
$\Sigma$
of TGDs. Let
![]() $\Sigma' \subseteq \Sigma$
and
$\Sigma' \subseteq \Sigma$
and
![]() $X \subseteq \mathit{chase}^\bot(D,\Sigma) \setminus D$
. Then,
$X \subseteq \mathit{chase}^\bot(D,\Sigma) \setminus D$
. Then,
![]() $\mathit{chase}(D \cup X, \Sigma') \subseteq \mathit{chase}(D, \Sigma)$
.
$\mathit{chase}(D \cup X, \Sigma') \subseteq \mathit{chase}(D, \Sigma)$
.
Proof. Let
![]() $X = \{\underline{a}_1,...,\underline{a}_n \}$
. For each
$X = \{\underline{a}_1,...,\underline{a}_n \}$
. For each
![]() $j \in [n]$
, let
$j \in [n]$
, let
![]() $\mathit{lev}(\underline{a}_i)$
be the level of
$\mathit{lev}(\underline{a}_i)$
be the level of
![]() $\underline{a}_i$
inside
$\underline{a}_i$
inside
![]() $\mathit{chase}(D, \Sigma)$
. Let
$\mathit{chase}(D, \Sigma)$
. Let
![]() $p = \max_{j \in [n]}\{\mathit{lev}(\underline{a}_i)\}$
. The proof proceeds by induction on the level i of
$p = \max_{j \in [n]}\{\mathit{lev}(\underline{a}_i)\}$
. The proof proceeds by induction on the level i of
![]() $\mathit{chase}(D \cup X, \Sigma')$
.
$\mathit{chase}(D \cup X, \Sigma')$
.
Base case:
![]() $i = 1$
. We want to prove that
$i = 1$
. We want to prove that
![]() $\mathit{chase}^1(D \cup X, \Sigma') \subseteq \mathit{chase}(D, \Sigma)$
. Let
$\mathit{chase}^1(D \cup X, \Sigma') \subseteq \mathit{chase}(D, \Sigma)$
. Let
![]() $\underline{a}$
be an atom of
$\underline{a}$
be an atom of
![]() $\mathit{chase}^1(D \cup X, \Sigma')$
generated exactly at level
$\mathit{chase}^1(D \cup X, \Sigma')$
generated exactly at level
![]() $i = 1$
. By definition,
$i = 1$
. By definition,
![]() $\underline{a}$
is obtained due to some trigger
$\underline{a}$
is obtained due to some trigger
![]() $\langle \sigma, h \rangle$
such that h maps
$\langle \sigma, h \rangle$
such that h maps
![]() $\mathit{body}(\sigma)$
to
$\mathit{body}(\sigma)$
to
![]() $D \cup X$
. If
$D \cup X$
. If
![]() $\underline{a} \in \mathit{chase}^p(D, \Sigma)$
, then the claim holds trivially. Otherwise, we can show that
$\underline{a} \in \mathit{chase}^p(D, \Sigma)$
, then the claim holds trivially. Otherwise, we can show that
![]() $\underline{a} \in \mathit{chase}^{p+1}(D, \Sigma)$
. Indeed, since h maps
$\underline{a} \in \mathit{chase}^{p+1}(D, \Sigma)$
. Indeed, since h maps
![]() $\mathit{body}(\sigma)$
to
$\mathit{body}(\sigma)$
to
![]() $D \cup X$
, then h is also a trigger involved at level
$D \cup X$
, then h is also a trigger involved at level
![]() $p+1$
since it maps
$p+1$
since it maps
![]() $\mathit{body}(\sigma)$
to
$\mathit{body}(\sigma)$
to
![]() $\mathit{chase}^{p}(D, \Sigma)$
. In particular, h maps at least one atom of
$\mathit{chase}^{p}(D, \Sigma)$
. In particular, h maps at least one atom of
![]() $\mathit{body}(\sigma)$
to some atom
$\mathit{body}(\sigma)$
to some atom
![]() $\underline{a}_k \in X$
such that
$\underline{a}_k \in X$
such that
![]() $\mathit{lev}(\underline{a}_k) = p$
. Since, by definition, nulls introduced during the chase functionally depend on the involved triggers, then
$\mathit{lev}(\underline{a}_k) = p$
. Since, by definition, nulls introduced during the chase functionally depend on the involved triggers, then
![]() $\underline{a}$
necessarily belongs to
$\underline{a}$
necessarily belongs to
![]() $\mathit{chase}^{p+1}(D, \Sigma)$
.
$\mathit{chase}^{p+1}(D, \Sigma)$
.
Induction step:
![]() $i = \ell$
. Given that for every level
$i = \ell$
. Given that for every level
![]() $i \leq \ell -1$
,
$i \leq \ell -1$
,
![]() $\mathit{chase}^{i}(D \cup X, \Sigma') \subseteq \mathit{chase}(D,\Sigma)$
(induction hypothesis), we prove that
$\mathit{chase}^{i}(D \cup X, \Sigma') \subseteq \mathit{chase}(D,\Sigma)$
(induction hypothesis), we prove that
![]() $ \mathit{chase}^{\ell}(D \cup X, \Sigma') \subseteq \mathit{chase}(D,\Sigma) $
holds, too. Let
$ \mathit{chase}^{\ell}(D \cup X, \Sigma') \subseteq \mathit{chase}(D,\Sigma) $
holds, too. Let
![]() $\beta$
be an atom of
$\beta$
be an atom of
![]() $ \mathit{chase}^{\ell}(D \cup X, \Sigma') $
generated exactly at level
$ \mathit{chase}^{\ell}(D \cup X, \Sigma') $
generated exactly at level
![]() $i=\ell$
. By definition,
$i=\ell$
. By definition,
![]() $\beta$
is obtained via some trigger
$\beta$
is obtained via some trigger
![]() $ \langle \sigma', h' \rangle $
such that h’ maps
$ \langle \sigma', h' \rangle $
such that h’ maps
![]() $\mathit{body}(\sigma')$
to atoms with level at most
$\mathit{body}(\sigma')$
to atoms with level at most
![]() $\ell-1$
. Accordingly, by induction hypothesis, h’ maps
$\ell-1$
. Accordingly, by induction hypothesis, h’ maps
![]() $\mathit{body}(\sigma')$
also to
$\mathit{body}(\sigma')$
also to
![]() $\mathit{chase}(D,\Sigma)$
. Hence, since the processing order of rules and triggers does not change the result of the chase and nulls functionally depend on the involved triggers, it follow that also
$\mathit{chase}(D,\Sigma)$
. Hence, since the processing order of rules and triggers does not change the result of the chase and nulls functionally depend on the involved triggers, it follow that also
![]() $\beta \in \mathit{chase}(D,\Sigma)$
.
$\beta \in \mathit{chase}(D,\Sigma)$
.
With the next proposition, we prove that Algorithm 2 always terminates and correctly constructs
![]() $D^+$
.
$D^+$
.
Proposition 4 Consider a database D and a
![]() ${{\mathcal{C}}}$
-dyadic pair
${{\mathcal{C}}}$
-dyadic pair
![]() $\Pi$
of TGDs. It holds that Algorithm 2 both terminates and computes
$\Pi$
of TGDs. It holds that Algorithm 2 both terminates and computes
![]() $D^+ = D \cup {{\mathit{gra}}}(D,\Pi)$
.
$D^+ = D \cup {{\mathit{gra}}}(D,\Pi)$
.
Proof. Let
![]() $\Pi = (\Sigma_\mathrm{HG}, \Sigma_\mathcal{C})$
. We proceed by proving first the termination of Algorithm 2 and then its correctness.
$\Pi = (\Sigma_\mathrm{HG}, \Sigma_\mathcal{C})$
. We proceed by proving first the termination of Algorithm 2 and then its correctness.
Termination. To prove the termination of Algorithm 2, it suffices to show that each instruction alone always terminates and that the overall procedure never falls into an infinite loop. First, observe that
![]() $|{{\mathit{gra}(D,\Pi)}}| \leq |\mathit{h}\textrm{-}\mathit{preds}(\Sigma_\mathrm{HG})|\cdot d^\mu$
, where
$|{{\mathit{gra}(D,\Pi)}}| \leq |\mathit{h}\textrm{-}\mathit{preds}(\Sigma_\mathrm{HG})|\cdot d^\mu$
, where
![]() $d=|\mathit{consts}(D)|$
and
$d=|\mathit{consts}(D)|$
and
![]() $ \mu = \max_{P \in \mathit{h}\textrm{-}\mathit{preds}(\Sigma_\mathrm{HG})}{\mathit{arity}(P)}$
. Instructions 1, 2, 4, 8, and 9 trivially terminate. Instructions 6 and 7 both terminate, since
$ \mu = \max_{P \in \mathit{h}\textrm{-}\mathit{preds}(\Sigma_\mathrm{HG})}{\mathit{arity}(P)}$
. Instructions 1, 2, 4, 8, and 9 trivially terminate. Instructions 6 and 7 both terminate, since
![]() $\tilde{D} \subseteq {{\mathit{gra}(D,\Pi)}}$
always holds (see correctness below). Each time instruction 3 is reached, the for-loop simply scans the set
$\tilde{D} \subseteq {{\mathit{gra}(D,\Pi)}}$
always holds (see correctness below). Each time instruction 3 is reached, the for-loop simply scans the set
![]() $\Sigma_\mathrm{HG}$
, which is finite by definition. Concerning instruction 5, it suffices to observe that its termination relies on the termination of cert-eval
$\Sigma_\mathrm{HG}$
, which is finite by definition. Concerning instruction 5, it suffices to observe that its termination relies on the termination of cert-eval
![]() ${{[{{\mathcal{C}}}]}}$
– which is true by hypothesis – and on the fact that, for each query q, to construct the set
${{[{{\mathcal{C}}}]}}$
– which is true by hypothesis – and on the fact that, for each query q, to construct the set
![]() $\{ \mathtt{H}_i(\mathbf{t}) \ | \ \mathbf{t} \in \mathit{cert}(q,D^+,\Sigma_\mathcal{C}) \}$
, the problem cert-eval
$\{ \mathtt{H}_i(\mathbf{t}) \ | \ \mathbf{t} \in \mathit{cert}(q,D^+,\Sigma_\mathcal{C}) \}$
, the problem cert-eval
![]() ${{[{{\mathcal{C}}}]}}$
must be solved at most
${{[{{\mathcal{C}}}]}}$
must be solved at most
![]() $d^\mu$
times, where
$d^\mu$
times, where
![]() $d^\mu$
is the maximum number of tuples t for which the check
$d^\mu$
is the maximum number of tuples t for which the check
![]() $\mathbf{t} \in \mathit{cert}(q,D^+,\Sigma_\mathcal{C})$
has to be performed. Since each instruction alone terminates, it remains to analyze the overall procedure. It contains two loops. The first, namely the for-loop at instruction 3, is not problematic; indeed, we shown that it locally terminates. The second one, namely the go to-loop, depends on the evaluation of the if-instruction, which can be executed at most
$\mathbf{t} \in \mathit{cert}(q,D^+,\Sigma_\mathcal{C})$
has to be performed. Since each instruction alone terminates, it remains to analyze the overall procedure. It contains two loops. The first, namely the for-loop at instruction 3, is not problematic; indeed, we shown that it locally terminates. The second one, namely the go to-loop, depends on the evaluation of the if-instruction, which can be executed at most
![]() $|{{\mathit{gra}(D,\Pi)}}|$
times. Thus, also the go to-loop does the same.
$|{{\mathit{gra}(D,\Pi)}}|$
times. Thus, also the go to-loop does the same.
Correctness. We now claim that Algorithm 2 correctly completes the database. Let
![]() $D^+$
be the output of Algorithm 2. Our claim is that
$D^+$
be the output of Algorithm 2. Our claim is that
![]() $D^+ = D \cup {{\mathit{gra}(D,\Pi)}}$
.
$D^+ = D \cup {{\mathit{gra}(D,\Pi)}}$
.
Inclusion 1 (
![]() $D^+ \supseteq D \cup {{\mathit{gra}(D,\Pi)}}$
). Assume, by contradiction, that
$D^+ \supseteq D \cup {{\mathit{gra}(D,\Pi)}}$
). Assume, by contradiction, that
![]() $D \cup {{\mathit{gra}(D,\Pi)}}$
contains some atom that does not belong to
$D \cup {{\mathit{gra}(D,\Pi)}}$
contains some atom that does not belong to
![]() $D^+$
. This means that there exists some
$D^+$
. This means that there exists some
![]() $j>0$
such that both
$j>0$
such that both
![]() $\bar{D} = ((D \cup {{\mathit{gra}(D,\Pi)}}) \cap \mathit{chase}^{j-1}(D, \Sigma_\mathrm{HG} \cup \Sigma_\mathcal{C})) \subseteq D^+$
and
$\bar{D} = ((D \cup {{\mathit{gra}(D,\Pi)}}) \cap \mathit{chase}^{j-1}(D, \Sigma_\mathrm{HG} \cup \Sigma_\mathcal{C})) \subseteq D^+$
and
![]() $((D \cup {{\mathit{gra}(D,\Pi)}}) \cap \mathit{chase}^j(D, \Sigma_\mathrm{HG} \cup \Sigma_\mathcal{C})) \setminus D^+ \neq \emptyset$
hold. Thus, there exists some
$((D \cup {{\mathit{gra}(D,\Pi)}}) \cap \mathit{chase}^j(D, \Sigma_\mathrm{HG} \cup \Sigma_\mathcal{C})) \setminus D^+ \neq \emptyset$
hold. Thus, there exists some
![]() $\underline{a} \in \mathit{chase}^j(D, \Sigma_\mathrm{HG} \cup \Sigma_\mathcal{C})$
whose level is exactly j and that does not belong to
$\underline{a} \in \mathit{chase}^j(D, \Sigma_\mathrm{HG} \cup \Sigma_\mathcal{C})$
whose level is exactly j and that does not belong to
![]() $D^+$
. Let
$D^+$
. Let
![]() $\langle \sigma, h\rangle$
be the trigger used by the chase to generate
$\langle \sigma, h\rangle$
be the trigger used by the chase to generate
![]() $\underline{a}$
, where
$\underline{a}$
, where
![]() $\sigma$
is of the form
$\sigma$
is of the form
![]() $\Phi(\mathbf{x,y}) \rightarrow \mathtt{H}(\mathbf{x})$
. Clearly, h maps
$\Phi(\mathbf{x,y}) \rightarrow \mathtt{H}(\mathbf{x})$
. Clearly, h maps
![]() $\Phi(\mathbf{x},\mathbf{y})$
to
$\Phi(\mathbf{x},\mathbf{y})$
to
![]() $\mathit{chase}^{j-1}(D, \Sigma_\mathrm{HG} \cup \Sigma_\mathcal{C})$
, and we also have that
$\mathit{chase}^{j-1}(D, \Sigma_\mathrm{HG} \cup \Sigma_\mathcal{C})$
, and we also have that
![]() $\underline{a} = \mathtt{H}(h(\mathbf{x}))$
. Consider now the query
$\underline{a} = \mathtt{H}(h(\mathbf{x}))$
. Consider now the query
![]() $q =\langle \mathbf{x} \rangle \leftarrow \Phi(\mathbf{x,y})$
constructed from
$q =\langle \mathbf{x} \rangle \leftarrow \Phi(\mathbf{x,y})$
constructed from
![]() $\sigma$
by Algorithm 2 at instruction 4. Thus,
$\sigma$
by Algorithm 2 at instruction 4. Thus,
![]() $\mathit{chase}^{j-1}(D, \Sigma_\mathrm{HG} \cup \Sigma_\mathcal{C}) \models q(h({\bf x}))$
holds. Since
$\mathit{chase}^{j-1}(D, \Sigma_\mathrm{HG} \cup \Sigma_\mathcal{C}) \models q(h({\bf x}))$
holds. Since
![]() $\bar{D} \subseteq D^+$
, we have that
$\bar{D} \subseteq D^+$
, we have that
![]() $\mathit{chase}^{j-1}(D, \Sigma_\mathrm{HG}\cup\Sigma_\mathcal{C}) \subseteq\mathit{chase}(\bar{D}, \Sigma_\mathcal{C})\subseteq\mathit{chase}(D^+, \Sigma_\mathcal{C})$
. Hence,
$\mathit{chase}^{j-1}(D, \Sigma_\mathrm{HG}\cup\Sigma_\mathcal{C}) \subseteq\mathit{chase}(\bar{D}, \Sigma_\mathcal{C})\subseteq\mathit{chase}(D^+, \Sigma_\mathcal{C})$
. Hence,
![]() $\mathit{chase}(D^+, \Sigma_\mathcal{C}) \models q(h({\bf x}))$
, namely
$\mathit{chase}(D^+, \Sigma_\mathcal{C}) \models q(h({\bf x}))$
, namely
![]() $h({\bf x}) \in \mathit{cert}(q,D^+,\Sigma_\mathcal{C})$
and, thus,
$h({\bf x}) \in \mathit{cert}(q,D^+,\Sigma_\mathcal{C})$
and, thus,
![]() $\underline{a} \in D^+$
, which is a contradiction.
$\underline{a} \in D^+$
, which is a contradiction.
Inclusion 2 (
![]() $D^+ \subseteq D \cup {{\mathit{gra}(D,\Pi)}}$
). Let
$D^+ \subseteq D \cup {{\mathit{gra}(D,\Pi)}}$
). Let
![]() $D^+$
be the set produced by Algorithm 2. Let
$D^+$
be the set produced by Algorithm 2. Let
![]() $\ell$
be the number of time instruction 7 of Algorithm 2 is executed. At each execution
$\ell$
be the number of time instruction 7 of Algorithm 2 is executed. At each execution
![]() $i \in [\ell]$
of instruction 7, the algorithm computes the set
$i \in [\ell]$
of instruction 7, the algorithm computes the set
![]() $\tilde{D}_i$
containing only auxiliary ground atoms, and produces the set
$\tilde{D}_i$
containing only auxiliary ground atoms, and produces the set
![]() $D^+_i = D \cup \tilde{D}_i$
. By construction,
$D^+_i = D \cup \tilde{D}_i$
. By construction,
![]() $D^+ = D \cup \tilde{D}_\ell$
. Let
$D^+ = D \cup \tilde{D}_\ell$
. Let
![]() $\tilde{D}_0 = \emptyset$
,
$\tilde{D}_0 = \emptyset$
,
![]() $D^+_0 = D \cup \tilde{D}_0$
, and
$D^+_0 = D \cup \tilde{D}_0$
, and
![]() $I_i = \tilde{D}_i \setminus \tilde{D}_{i-1}$
, for each
$I_i = \tilde{D}_i \setminus \tilde{D}_{i-1}$
, for each
![]() $i \in [\ell]$
. We show that
$i \in [\ell]$
. We show that
![]() $D \cup \tilde{D}_\ell \subseteq D \cup {{\mathit{gra}(D,\Pi)}}$
, that is
$D \cup \tilde{D}_\ell \subseteq D \cup {{\mathit{gra}(D,\Pi)}}$
, that is
![]() $\tilde{D}_\ell \subseteq {{\mathit{gra}(D,\Pi)}}$
. We proceed by induction on the number
$\tilde{D}_\ell \subseteq {{\mathit{gra}(D,\Pi)}}$
. We proceed by induction on the number
![]() $\ell$
of iterations.
$\ell$
of iterations.
Base case: Let
![]() $i = 1$
. We claim that
$i = 1$
. We claim that
![]() $ \tilde{D}_1 \subseteq {{\mathit{gra}(D,\Pi)}} $
. By construction, the set
$ \tilde{D}_1 \subseteq {{\mathit{gra}(D,\Pi)}} $
. By construction, the set
![]() $\tilde{D}_1 = \{ \mathtt{H}_i(\mathbf{t}) ~|~ i \in [|\Sigma_\mathrm{HG}|] ~\wedge~ \mathbf{t} \in \mathit{cert}(q, D^+_0, \Sigma_\mathcal{C}) \}$
. Since
$\tilde{D}_1 = \{ \mathtt{H}_i(\mathbf{t}) ~|~ i \in [|\Sigma_\mathrm{HG}|] ~\wedge~ \mathbf{t} \in \mathit{cert}(q, D^+_0, \Sigma_\mathcal{C}) \}$
. Since
![]() $D^+_0 = D$
and the component
$D^+_0 = D$
and the component
![]() $\Sigma_\mathcal{C}$
does not produce any atom in the first iteration of the algorithm, the latter is equal to
$\Sigma_\mathcal{C}$
does not produce any atom in the first iteration of the algorithm, the latter is equal to
![]() $\{ \mathtt{H}(\mathbf{t}) ~|~ i \in [|\Sigma_\mathrm{HG}|] ~\wedge~ \mathbf{t} \in \mathit{cert}(q, D, \emptyset) \}= \{ \underline{a} \in \mathit{chase}^1(D, \Sigma_\mathrm{HG}) ~|~ \mathit{preds}(\underline{a}) \in \mathit{h}\textrm{-}\mathit{preds}(\Sigma_\mathrm{HG}) \}\subseteq \{ \underline{a} \in \mathit{chase}(D, \Sigma_\mathrm{HG} \cup \Sigma_\mathcal{C}) ~|~ \mathit{preds}(\underline{a}) \in \mathit{h}\textrm{-}\mathit{preds}(\Sigma_\mathrm{HG}) \} = {{\mathit{gra}(D,\Pi)}}$
.
$\{ \mathtt{H}(\mathbf{t}) ~|~ i \in [|\Sigma_\mathrm{HG}|] ~\wedge~ \mathbf{t} \in \mathit{cert}(q, D, \emptyset) \}= \{ \underline{a} \in \mathit{chase}^1(D, \Sigma_\mathrm{HG}) ~|~ \mathit{preds}(\underline{a}) \in \mathit{h}\textrm{-}\mathit{preds}(\Sigma_\mathrm{HG}) \}\subseteq \{ \underline{a} \in \mathit{chase}(D, \Sigma_\mathrm{HG} \cup \Sigma_\mathcal{C}) ~|~ \mathit{preds}(\underline{a}) \in \mathit{h}\textrm{-}\mathit{preds}(\Sigma_\mathrm{HG}) \} = {{\mathit{gra}(D,\Pi)}}$
.
Induction step: Given that, for
![]() $i = \ell-1, \ \tilde{D}_{\ell -1} \subseteq {{\mathit{gra}(D,\Pi)}} $
(induction hypothesis), we prove that
$i = \ell-1, \ \tilde{D}_{\ell -1} \subseteq {{\mathit{gra}(D,\Pi)}} $
(induction hypothesis), we prove that
![]() $ \tilde{D}_\ell \subseteq {{\mathit{gra}(D,\Pi)}} $
holds, too. By construction
$ \tilde{D}_\ell \subseteq {{\mathit{gra}(D,\Pi)}} $
holds, too. By construction
![]() $\tilde{D}_\ell = \{ \mathtt{H}_i(\mathbf{t}) ~|~ i \in [|\Sigma_\mathrm{HG}|] ~\wedge~ \mathbf{t} \in \mathit{cert}(q, D^+_{\ell-1}, \Sigma_\mathcal{C}) \}= \{ \mathtt{H}_i(\mathbf{t}) ~|~ i \in [|\Sigma_\mathrm{HG}|] ~\wedge~ \mathbf{t} \in \mathit{cert}(q, D \cup \tilde{D}_{\ell-1}, \Sigma_\mathcal{C}) \}= \{ \underline{a} \in \mathit{chase}(D \cup \tilde{D}_{\ell-1}, \Sigma_\mathrm{HG} \cup \Sigma_\mathcal{C}) ~|~ \mathit{preds}(\underline{a}) \in \mathit{h}\textrm{-}\mathit{preds}(\Sigma_\mathrm{HG}) \}$
. Since the set
$\tilde{D}_\ell = \{ \mathtt{H}_i(\mathbf{t}) ~|~ i \in [|\Sigma_\mathrm{HG}|] ~\wedge~ \mathbf{t} \in \mathit{cert}(q, D^+_{\ell-1}, \Sigma_\mathcal{C}) \}= \{ \mathtt{H}_i(\mathbf{t}) ~|~ i \in [|\Sigma_\mathrm{HG}|] ~\wedge~ \mathbf{t} \in \mathit{cert}(q, D \cup \tilde{D}_{\ell-1}, \Sigma_\mathcal{C}) \}= \{ \underline{a} \in \mathit{chase}(D \cup \tilde{D}_{\ell-1}, \Sigma_\mathrm{HG} \cup \Sigma_\mathcal{C}) ~|~ \mathit{preds}(\underline{a}) \in \mathit{h}\textrm{-}\mathit{preds}(\Sigma_\mathrm{HG}) \}$
. Since the set
![]() $ D \cup \tilde{D}_{\ell-1}$
already contains all the ground consequences of
$ D \cup \tilde{D}_{\ell-1}$
already contains all the ground consequences of
![]() $\Sigma_\mathrm{HG}$
, the latter is equivalent to
$\Sigma_\mathrm{HG}$
, the latter is equivalent to
![]() $\{ \underline{a} \in \mathit{chase}(D \cup \tilde{D}_{\ell-1}, \Sigma_\mathcal{C}) ~|~ \mathit{preds}(\underline{a}) \in \mathit{h}\textrm{-}\mathit{preds}(\Sigma_\mathrm{HG}) \}$
. Applying Lemma 1 together with the induction hypothesis, the last one is a subset of
$\{ \underline{a} \in \mathit{chase}(D \cup \tilde{D}_{\ell-1}, \Sigma_\mathcal{C}) ~|~ \mathit{preds}(\underline{a}) \in \mathit{h}\textrm{-}\mathit{preds}(\Sigma_\mathrm{HG}) \}$
. Applying Lemma 1 together with the induction hypothesis, the last one is a subset of
![]() $ \{ \underline{a} \in \mathit{chase}(D, \Sigma_\mathrm{HG} \cup \Sigma_\mathcal{C}) ~|~ \mathit{preds}(\underline{a}) \in \mathit{h}\textrm{-}\mathit{preds}(\Sigma_\mathrm{HG}) \} = {{\mathit{gra}(D,\Pi)}}$
.
$ \{ \underline{a} \in \mathit{chase}(D, \Sigma_\mathrm{HG} \cup \Sigma_\mathcal{C}) ~|~ \mathit{preds}(\underline{a}) \in \mathit{h}\textrm{-}\mathit{preds}(\Sigma_\mathrm{HG}) \} = {{\mathit{gra}(D,\Pi)}}$
.
We conclude the section by proving the decidability of the problem dp-cert-eval
![]() ${{[{{\mathcal{C}}}]}}$
, under the assumption that cert-eval
${{[{{\mathcal{C}}}]}}$
, under the assumption that cert-eval
![]() ${{[{{\mathcal{C}}}]}}$
is decidable.
${{[{{\mathcal{C}}}]}}$
is decidable.
Theorem 2 If cert-eval
![]() ${{[{{\mathcal{C}}}]}}$
is decidable, then dp-cert-eval
${{[{{\mathcal{C}}}]}}$
is decidable, then dp-cert-eval
![]() ${{[{{\mathcal{C}}}]}}$
is decidable.
${{[{{\mathcal{C}}}]}}$
is decidable.
Proof. To prove the decidability of dp-cert-eval
![]() ${{[{{\mathcal{C}}}]}}$
we design Algorithm 1. Let D be a database,
${{[{{\mathcal{C}}}]}}$
we design Algorithm 1. Let D be a database,
![]() $\Pi=(\Sigma_\mathrm{HG},\Sigma_\mathcal{C})$
a dyadic pair,
$\Pi=(\Sigma_\mathrm{HG},\Sigma_\mathcal{C})$
a dyadic pair,
![]() $q(\mathbf{x})$
a CQ, and
$q(\mathbf{x})$
a CQ, and
![]() $\mathbf{c}$
a tuple in
$\mathbf{c}$
a tuple in
![]() $\mathsf{C}^{\mathbf{x}}$
. Clearly, step 1 always terminates since it recalls Algorithm 2 that, as shown in Proposition 4, always terminates and correctly constructs the set
$\mathsf{C}^{\mathbf{x}}$
. Clearly, step 1 always terminates since it recalls Algorithm 2 that, as shown in Proposition 4, always terminates and correctly constructs the set
![]() $D^+$
. By Theorem 1, checking if
$D^+$
. By Theorem 1, checking if
![]() $\mathbf{c} \in {{\mathit{dp}\textrm{-}\mathit{cert}}}(q,D,\Pi)$
boils down to checking if
$\mathbf{c} \in {{\mathit{dp}\textrm{-}\mathit{cert}}}(q,D,\Pi)$
boils down to checking if
![]() $\mathbf{c} \in \mathit{cert}(q,D^+,\Sigma_\mathcal{C})$
, that is decidable by hypothesis. Hence, step 2 never falls in a loop and Algorithm 1 correctly computes dp-cert-eval
$\mathbf{c} \in \mathit{cert}(q,D^+,\Sigma_\mathcal{C})$
, that is decidable by hypothesis. Hence, step 2 never falls in a loop and Algorithm 1 correctly computes dp-cert-eval
![]() ${{[{{\mathcal{C}}}]}}$
.
${{[{{\mathcal{C}}}]}}$
.
5 Dyadic decomposable sets
In this section we introduce a novel general condition that allows to define, from any decidable class
![]() $\mathcal{C}$
of ontologies, a new decidable class called
$\mathcal{C}$
of ontologies, a new decidable class called
![]() ${{\textsf{Dyadic-}\mathcal{C}}}$
enjoying desirable properties. The union of all the
${{\textsf{Dyadic-}\mathcal{C}}}$
enjoying desirable properties. The union of all the
![]() ${{\textsf{Dyadic-}\mathcal{C}}}$
classes, with
${{\textsf{Dyadic-}\mathcal{C}}}$
classes, with
![]() $\mathcal{C}$
being any decidable class of TGDs, forms what we call dyadic decomposable sets, which encompass and generalize any other existing decidable class, including those based on semantic conditions.
$\mathcal{C}$
being any decidable class of TGDs, forms what we call dyadic decomposable sets, which encompass and generalize any other existing decidable class, including those based on semantic conditions.
We start the section by providing a classification of atoms of the rule-body, according to where dangerous variables appear; then we define the class
![]() ${{\textsf{Dyadic-}\mathcal{C}}}$
proving that the query answer problem over this class is decidable.
${{\textsf{Dyadic-}\mathcal{C}}}$
proving that the query answer problem over this class is decidable.
Definition 6 (Atoms classification) Consider a set
![]() $\Sigma$
of TGDs and a rule
$\Sigma$
of TGDs and a rule
![]() $\sigma \in \Sigma$
. An atom
$\sigma \in \Sigma$
. An atom
![]() $\underline{a}$
of
$\underline{a}$
of
![]() $\mathit{body}(\sigma)$
is
$\mathit{body}(\sigma)$
is
![]() $\sigma$
-problematic if (i)
$\sigma$
-problematic if (i)
![]() $\underline{a}$
contains a dangerous variable w.r.t.
$\underline{a}$
contains a dangerous variable w.r.t.
![]() $\Sigma$
, or (ii)
$\Sigma$
, or (ii)
![]() $\underline{a}$
is connected to some
$\underline{a}$
is connected to some
![]() $\sigma$
-problematic atom via some harmful variable. The set of all the problematic atoms of
$\sigma$
-problematic atom via some harmful variable. The set of all the problematic atoms of
![]() $\sigma$
is denoted by
$\sigma$
is denoted by
![]() ${{\mathit{p}\textrm{-}\mathit{atoms}}}(\sigma)$
, whereas
${{\mathit{p}\textrm{-}\mathit{atoms}}}(\sigma)$
, whereas
![]() ${{\mathit{s}\textrm{-}\mathit{atoms}}}(\sigma) = \mathit{body}(\sigma) \setminus {{\mathit{p}\textrm{-}\mathit{atoms}}}(\sigma)$
denotes the set of all the safe atoms of
${{\mathit{s}\textrm{-}\mathit{atoms}}}(\sigma) = \mathit{body}(\sigma) \setminus {{\mathit{p}\textrm{-}\mathit{atoms}}}(\sigma)$
denotes the set of all the safe atoms of
![]() $\sigma$
.
$\sigma$
.
![]()
We highlight that
![]() ${{\mathit{p}\textrm{-}\mathit{atoms}}}$
and
${{\mathit{p}\textrm{-}\mathit{atoms}}}$
and
![]() ${{\mathit{s}\textrm{-}\mathit{atoms}}}$
can share only harmless variables. The next example is to clarify the above definition.
${{\mathit{s}\textrm{-}\mathit{atoms}}}$
can share only harmless variables. The next example is to clarify the above definition.
Example 3 Consider the database
![]() $D=\{L(a),R(a,b)\}$
, and the following set
$D=\{L(a),R(a,b)\}$
, and the following set
![]() $\Sigma$
of TGDs:
$\Sigma$
of TGDs:
 $$\begin{array}{rrcl}\sigma_1: & L(x_1) & \rightarrow & \exists ~ y_1 ~ P(y_1,x_1) \\\sigma_2: & P(x_2,y_2) & \rightarrow & \exists ~ z_2 ~ Q(y_2,z_2,x_2) \\\sigma_3: & P(z_3,x_3), Q(x_3,y_3,z_3) & \rightarrow & S(z_3)\\\sigma_4: & P(x_4,y_4), Q(y_4,z_4,w_4), S(w_4), R(u_4,v_4) & \rightarrow & T(x_4,z_4,u_4).\end{array}$$
$$\begin{array}{rrcl}\sigma_1: & L(x_1) & \rightarrow & \exists ~ y_1 ~ P(y_1,x_1) \\\sigma_2: & P(x_2,y_2) & \rightarrow & \exists ~ z_2 ~ Q(y_2,z_2,x_2) \\\sigma_3: & P(z_3,x_3), Q(x_3,y_3,z_3) & \rightarrow & S(z_3)\\\sigma_4: & P(x_4,y_4), Q(y_4,z_4,w_4), S(w_4), R(u_4,v_4) & \rightarrow & T(x_4,z_4,u_4).\end{array}$$
We focus on rule
![]() $\sigma_4$
. Taking into account that
$\sigma_4$
. Taking into account that
![]() $\mathit{aff}(\Sigma)=\{P[1],S[1],Q[2],Q[3]\}$
, it follows that
$\mathit{aff}(\Sigma)=\{P[1],S[1],Q[2],Q[3]\}$
, it follows that
![]() $\mathit{dang}(\Sigma)=\{x_2,x_4,z_3,z_4\}$
,
$\mathit{dang}(\Sigma)=\{x_2,x_4,z_3,z_4\}$
,
![]() $\mathit{harmful}(\Sigma)=\{x_2,x_4,y_3,z_3,z_4,w_4\}$
, and
$\mathit{harmful}(\Sigma)=\{x_2,x_4,y_3,z_3,z_4,w_4\}$
, and
![]() $\mathit{harmless}(\Sigma)=\{x_1,x_3,y_2,y_4,u_4,v_4\}$
. Hence,
$\mathit{harmless}(\Sigma)=\{x_1,x_3,y_2,y_4,u_4,v_4\}$
. Hence,
![]() ${{\mathit{p}\textrm{-}\mathit{atoms}}}(\sigma_4) = \{P(x_4,y_4), Q(y_4,z_4,w_4), S(w_4)\} $
, whereas
${{\mathit{p}\textrm{-}\mathit{atoms}}}(\sigma_4) = \{P(x_4,y_4), Q(y_4,z_4,w_4), S(w_4)\} $
, whereas
![]() ${{\mathit{s}\textrm{-}\mathit{atoms}}}(\sigma_4) = \{R(u_4,v_4)\}$
.
${{\mathit{s}\textrm{-}\mathit{atoms}}}(\sigma_4) = \{R(u_4,v_4)\}$
.
![]()
The second step consists in selecting variables shared by
![]() ${{\mathit{p}\textrm{-}\mathit{atoms}}}$
and
${{\mathit{p}\textrm{-}\mathit{atoms}}}$
and
![]() ${{\mathit{s}\textrm{-}\mathit{atoms}}}$
together with the harmless frontier variables appearing in
${{\mathit{s}\textrm{-}\mathit{atoms}}}$
together with the harmless frontier variables appearing in
![]() ${{\mathit{s}\textrm{-}\mathit{atoms}}}$
. The latter can be expressed via the set
${{\mathit{s}\textrm{-}\mathit{atoms}}}$
. The latter can be expressed via the set
![]() ${{\mathit{hf}}}(\sigma) = \{ x \in \mathit{vars}({{\mathit{s}\textrm{-}\mathit{atoms}}}{(\sigma)}) ~|~ x \in \mathit{harmless}(\sigma) ~\wedge~ x \in \mathsf{vars_\curvearrowright}(\sigma) \}$
. Then, we define
${{\mathit{hf}}}(\sigma) = \{ x \in \mathit{vars}({{\mathit{s}\textrm{-}\mathit{atoms}}}{(\sigma)}) ~|~ x \in \mathit{harmless}(\sigma) ~\wedge~ x \in \mathsf{vars_\curvearrowright}(\sigma) \}$
. Then, we define
![]() $\mathit{vars}_\star(\sigma) = \{\mathit{vars}({{\mathit{p}\textrm{-}\mathit{atoms}}}{(\sigma)}) ~\cap~ \mathit{vars}({{\mathit{s}\textrm{-}\mathit{atoms}}}{(\sigma)})\} ~ \cup ~ {{\mathit{hf}}}(\sigma)$
. Trivially, it holds that
$\mathit{vars}_\star(\sigma) = \{\mathit{vars}({{\mathit{p}\textrm{-}\mathit{atoms}}}{(\sigma)}) ~\cap~ \mathit{vars}({{\mathit{s}\textrm{-}\mathit{atoms}}}{(\sigma)})\} ~ \cup ~ {{\mathit{hf}}}(\sigma)$
. Trivially, it holds that
![]() $\mathit{vars}_\star(\sigma) \subseteq \mathit{vars}({{\mathit{s}\textrm{-}\mathit{atoms}}}{(\sigma)})$
. Finally, let
$\mathit{vars}_\star(\sigma) \subseteq \mathit{vars}({{\mathit{s}\textrm{-}\mathit{atoms}}}{(\sigma)})$
. Finally, let
By considering again Example 3, we have that
![]() $\mathit{vars}_\star(\sigma_4)=\{u_4,y_4\}$
and also that
$\mathit{vars}_\star(\sigma_4)=\{u_4,y_4\}$
and also that
![]() $\mathit{main}(\sigma_4): \mathtt{Aux}_{\sigma_4}(u_4,y_4),P(x_4,y_4), Q(y_4,z_4,w_4), S(w_4,y_4) \rightarrow T(x_4,z_4,u_4)$
.
$\mathit{main}(\sigma_4): \mathtt{Aux}_{\sigma_4}(u_4,y_4),P(x_4,y_4), Q(y_4,z_4,w_4), S(w_4,y_4) \rightarrow T(x_4,z_4,u_4)$
.
In the special case in which a variable x of
![]() $\mathit{vars}_\star(\sigma)$
occurs
$\mathit{vars}_\star(\sigma)$
occurs
![]() $n>1$
times in
$n>1$
times in
![]() $\mathit{head}(\sigma)$
, then x also occurs n times in the head of
$\mathit{head}(\sigma)$
, then x also occurs n times in the head of
![]() $\mathit{hg}(\sigma)$
. Accordingly, x occurs with different names (e.g.,
$\mathit{hg}(\sigma)$
. Accordingly, x occurs with different names (e.g.,
![]() $x_1,...,x_n$
) both in the head and in the body of
$x_1,...,x_n$
) both in the head and in the body of
![]() $\mathit{main}(\sigma)$
. For example, if the ontology contains only the rule
$\mathit{main}(\sigma)$
. For example, if the ontology contains only the rule
![]() $\sigma : P(x) \rightarrow R(x,x)$
, then
$\sigma : P(x) \rightarrow R(x,x)$
, then
![]() $\mathit{hg}(\sigma): P(x) \rightarrow \mathtt{Aux}_\sigma(x,x) $
and
$\mathit{hg}(\sigma): P(x) \rightarrow \mathtt{Aux}_\sigma(x,x) $
and
![]() $\mathit{main}(\sigma): \mathtt{Aux}_\sigma(x_1,x_2) \rightarrow R(x_1,x_2)$
. Clearly, the latter two rules together are equivalent to
$\mathit{main}(\sigma): \mathtt{Aux}_\sigma(x_1,x_2) \rightarrow R(x_1,x_2)$
. Clearly, the latter two rules together are equivalent to
![]() $\sigma$
w.r.t. to the schema
$\sigma$
w.r.t. to the schema
![]() $\{P,R\}$
. We prefer to keep the formal definition of
$\{P,R\}$
. We prefer to keep the formal definition of
![]() $\mathit{hg}(\Sigma)$
and
$\mathit{hg}(\Sigma)$
and
![]() $\mathit{main}(\Sigma)$
light without formalizing such special cases.
$\mathit{main}(\Sigma)$
light without formalizing such special cases.
We are now ready to formally introduce the class
![]() ${{\textsf{Dyadic-}\mathcal{C}}}$
.
${{\textsf{Dyadic-}\mathcal{C}}}$
.
Definition 7 (
![]() ${{\textsf{Dyadic-}\mathcal{C}}}$
) Consider a class
${{\textsf{Dyadic-}\mathcal{C}}}$
) Consider a class
![]() ${{\mathcal{C}}}$
of TGDs such that cert-eval
${{\mathcal{C}}}$
of TGDs such that cert-eval
![]() ${{[{{\mathcal{C}}}]}}$
is decidable. We say that
${{[{{\mathcal{C}}}]}}$
is decidable. We say that
![]() $\Sigma$
belongs to
$\Sigma$
belongs to
![]() ${{\textsf{Dyadic-}\mathcal{C}}}$
if
${{\textsf{Dyadic-}\mathcal{C}}}$
if
![]() $\Sigma$
belongs to
$\Sigma$
belongs to
![]() ${{\mathcal{C}}}$
or if
${{\mathcal{C}}}$
or if
![]() $\mathit{main}(\Sigma)$
belongs to
$\mathit{main}(\Sigma)$
belongs to
![]() ${{\mathcal{C}}}$
.
${{\mathcal{C}}}$
.
![]()
According to the previous definition, one can easily state the following property.
Proposition 5 Consider a class
![]() ${{\mathcal{C}}}$
of TGDs. It holds that
${{\mathcal{C}}}$
of TGDs. It holds that
![]() ${{\mathcal{C}}} \subseteq {{\textsf{Dyadic-}\mathcal{C}}}$
.
${{\mathcal{C}}} \subseteq {{\textsf{Dyadic-}\mathcal{C}}}$
.
By Definition 7, to check if an ontology
![]() $\Sigma$
belongs to
$\Sigma$
belongs to
![]() ${{\textsf{Dyadic-}\mathcal{C}}}$
, one has to verify if
${{\textsf{Dyadic-}\mathcal{C}}}$
, one has to verify if
![]() $\Sigma \in {{\mathcal{C}}}$
, or
$\Sigma \in {{\mathcal{C}}}$
, or
![]() $\mathit{main}(\Sigma) \in {{\mathcal{C}}}$
. We observe that the construction of the set
$\mathit{main}(\Sigma) \in {{\mathcal{C}}}$
. We observe that the construction of the set
![]() $\mathit{main}(\Sigma)$
explained above, is polynomial (indeed linear) with respect to the size of
$\mathit{main}(\Sigma)$
explained above, is polynomial (indeed linear) with respect to the size of
![]() $\Sigma$
. Hence, the following result holds.
$\Sigma$
. Hence, the following result holds.
Theorem 3 Consider a class
![]() ${{\mathcal{C}}}$
of TGDs and assume that checking whether an ontology belongs to
${{\mathcal{C}}}$
of TGDs and assume that checking whether an ontology belongs to
![]() ${{\mathcal{C}}}$
is doable in some complexity class
${{\mathcal{C}}}$
is doable in some complexity class
![]() $\mathbb{C} \supseteq { \textbf{PTIME}}$
. Then, checking whether an ontology belongs to
$\mathbb{C} \supseteq { \textbf{PTIME}}$
. Then, checking whether an ontology belongs to
![]() ${{\textsf{Dyadic-}\mathcal{C}}}$
is decidable and it belongs to
${{\textsf{Dyadic-}\mathcal{C}}}$
is decidable and it belongs to
![]() $\mathbb{C}$
.
$\mathbb{C}$
.
Proof. We start recalling that, by Definition 7, an ontology
![]() $\Sigma$
belongs to
$\Sigma$
belongs to
![]() ${{\textsf{Dyadic-}\mathcal{C}}}$
if (i)
${{\textsf{Dyadic-}\mathcal{C}}}$
if (i)
![]() $\Sigma \in {{\mathcal{C}}}$
, or (ii)
$\Sigma \in {{\mathcal{C}}}$
, or (ii)
![]() $\mathit{main}(\Sigma) \in {{\mathcal{C}}}$
. Accordingly, checking condition (i) is doable in some complexity class
$\mathit{main}(\Sigma) \in {{\mathcal{C}}}$
. Accordingly, checking condition (i) is doable in some complexity class
![]() $\mathbb{C} \supseteq { \textbf{PTIME}}$
, by assumption; otherwise, the construction of the set
$\mathbb{C} \supseteq { \textbf{PTIME}}$
, by assumption; otherwise, the construction of the set
![]() $\mathit{main}(\Sigma)$
is done by a procedure that is polynomial (indeed linear) with respect to the size of
$\mathit{main}(\Sigma)$
is done by a procedure that is polynomial (indeed linear) with respect to the size of
![]() $\Sigma$
and, hence, always terminates. Accordingly, checking condition (ii) is also decidable and doable in the complexity class
$\Sigma$
and, hence, always terminates. Accordingly, checking condition (ii) is also decidable and doable in the complexity class
![]() $\mathbb{C}$
.
$\mathbb{C}$
.
The next step is to prove the existence of a
![]() ${{\mathcal{C}}}$
-dyadic pair for any ontology
${{\mathcal{C}}}$
-dyadic pair for any ontology
![]() $\Sigma \in {{\textsf{Dyadic-}\mathcal{C}}}$
.
$\Sigma \in {{\textsf{Dyadic-}\mathcal{C}}}$
.
Theorem 4 Consider a set
![]() $\Sigma \in {{\textsf{Dyadic-}\mathcal{C}}}$
. There exists a
$\Sigma \in {{\textsf{Dyadic-}\mathcal{C}}}$
. There exists a
![]() ${{\mathcal{C}}}$
-dyadic pair
${{\mathcal{C}}}$
-dyadic pair
![]() $\Pi = (\Sigma_\mathrm{HG}, \Sigma_\mathcal{C})$
of TGDs such that
$\Pi = (\Sigma_\mathrm{HG}, \Sigma_\mathcal{C})$
of TGDs such that
![]() $\Sigma_\mathrm{HG} \cup \Sigma_\mathcal{C} \equiv_{\mathbf{\mathit{sch}(\Sigma)}} \Sigma$
. In particular,
$\Sigma_\mathrm{HG} \cup \Sigma_\mathcal{C} \equiv_{\mathbf{\mathit{sch}(\Sigma)}} \Sigma$
. In particular,
1. If
 $\Sigma \in {{\mathcal{C}}}$
, then
$\Sigma \in {{\mathcal{C}}}$
, then
 $\Sigma_\mathrm{HG} = \emptyset$
and
$\Sigma_\mathrm{HG} = \emptyset$
and
 $\Sigma_\mathcal{C} = \Sigma$
;
$\Sigma_\mathcal{C} = \Sigma$
;2. If
 $\Sigma \not\in {{\mathcal{C}}}$
, then
$\Sigma \not\in {{\mathcal{C}}}$
, then
 $\Sigma_\mathrm{HG} = \mathit{hg}(\Sigma)$
and
$\Sigma_\mathrm{HG} = \mathit{hg}(\Sigma)$
and
 $\Sigma_\mathcal{C} = \mathit{main}(\Sigma)$
.
$\Sigma_\mathcal{C} = \mathit{main}(\Sigma)$
.
Proof. We claim that for each ontology
![]() $\Sigma \in {{\textsf{Dyadic-}\mathcal{C}}}$
it is possible to construct a
$\Sigma \in {{\textsf{Dyadic-}\mathcal{C}}}$
it is possible to construct a
![]() ${{\mathcal{C}}}$
-dyadic pair
${{\mathcal{C}}}$
-dyadic pair
![]() $\Pi = (\Sigma_\mathrm{HG}, \Sigma_\mathcal{C})$
of TGDs such that
$\Pi = (\Sigma_\mathrm{HG}, \Sigma_\mathcal{C})$
of TGDs such that
![]() $\Sigma_\mathrm{HG} \cup \Sigma_\mathcal{C} \equiv_{\mathbf{\mathit{sch}(\Sigma)}} \Sigma$
.
$\Sigma_\mathrm{HG} \cup \Sigma_\mathcal{C} \equiv_{\mathbf{\mathit{sch}(\Sigma)}} \Sigma$
.
According to Definition 5, we recall that a pair
![]() $\Pi = (\Sigma_\mathrm{HG}, \Sigma_\mathcal{C})$
is
$\Pi = (\Sigma_\mathrm{HG}, \Sigma_\mathcal{C})$
is
![]() ${{\mathcal{C}}}$
-dyadic if (i)
${{\mathcal{C}}}$
-dyadic if (i)
![]() $\Sigma_\mathrm{HG}$
is head-ground with respect to
$\Sigma_\mathrm{HG}$
is head-ground with respect to
![]() $\Sigma_\mathrm{HG} \cup \Sigma_\mathcal{C}$
and (ii)
$\Sigma_\mathrm{HG} \cup \Sigma_\mathcal{C}$
and (ii)
![]() $\Sigma_\mathcal{C} \in {{\mathcal{C}}}$
. Assume first that
$\Sigma_\mathcal{C} \in {{\mathcal{C}}}$
. Assume first that
![]() $\Sigma \in {{\mathcal{C}}}$
. Then, trivially the pair
$\Sigma \in {{\mathcal{C}}}$
. Then, trivially the pair
![]() $(\emptyset,\Sigma)$
is a
$(\emptyset,\Sigma)$
is a
![]() ${{\mathcal{C}}}$
-dyadic pair. Assume now that
${{\mathcal{C}}}$
-dyadic pair. Assume now that
![]() $\Sigma \notin {{\mathcal{C}}}$
and let
$\Sigma \notin {{\mathcal{C}}}$
and let
![]() $\Pi = (\mathit{hg}(\Sigma), \mathit{main}(\Sigma))$
. Property (ii) is satisfied since by hypothesis
$\Pi = (\mathit{hg}(\Sigma), \mathit{main}(\Sigma))$
. Property (ii) is satisfied since by hypothesis
![]() $\Sigma \in {{\textsf{Dyadic-}\mathcal{C}}}$
; hence, it follows by definition that
$\Sigma \in {{\textsf{Dyadic-}\mathcal{C}}}$
; hence, it follows by definition that
![]() $\mathit{main}(\Sigma) \in {{\mathcal{C}}}$
. It remains to show property (i). According to Definition 4, the set
$\mathit{main}(\Sigma) \in {{\mathcal{C}}}$
. It remains to show property (i). According to Definition 4, the set
![]() $\mathit{hg}(\Sigma)$
has to satisfy four properties. Property 1 and 2 are trivially fulfilled since, by construction, for each
$\mathit{hg}(\Sigma)$
has to satisfy four properties. Property 1 and 2 are trivially fulfilled since, by construction, for each
![]() $\sigma \in \Sigma$
,
$\sigma \in \Sigma$
,
![]() $\mathit{hg}(\sigma)$
is a datalog rule and each head atom contains only harmless variables with respect to
$\mathit{hg}(\sigma)$
is a datalog rule and each head atom contains only harmless variables with respect to
![]() $\mathit{hg}(\Sigma) \cup \mathit{main}(\Sigma)$
. Property 3 and 4 state that
$\mathit{hg}(\Sigma) \cup \mathit{main}(\Sigma)$
. Property 3 and 4 state that
![]() $\mathit{h}\textrm{-}\mathit{preds}(\mathit{hg}(\Sigma)) \cap \mathit{b}\textrm{-}\mathit{preds}(\mathit{hg}(\Sigma)) = \emptyset$
and
$\mathit{h}\textrm{-}\mathit{preds}(\mathit{hg}(\Sigma)) \cap \mathit{b}\textrm{-}\mathit{preds}(\mathit{hg}(\Sigma)) = \emptyset$
and
![]() $ \mathit{h}\textrm{-}\mathit{preds}(\mathit{hg}(\Sigma)) \cap \mathit{h}\textrm{-}\mathit{preds}(\mathit{main}(\Sigma)) = \emptyset $
. These hold since, by construction,
$ \mathit{h}\textrm{-}\mathit{preds}(\mathit{hg}(\Sigma)) \cap \mathit{h}\textrm{-}\mathit{preds}(\mathit{main}(\Sigma)) = \emptyset $
. These hold since, by construction,
![]() $\mathit{h}\textrm{-}\mathit{preds}(\mathit{hg}(\Sigma)) = \{\mathtt{Aux}_{\sigma} : \sigma \in \Sigma\}$
, where each
$\mathit{h}\textrm{-}\mathit{preds}(\mathit{hg}(\Sigma)) = \{\mathtt{Aux}_{\sigma} : \sigma \in \Sigma\}$
, where each
![]() $\mathtt{Aux}_{\sigma}$
is a predicate that does not occur neither in any body of
$\mathtt{Aux}_{\sigma}$
is a predicate that does not occur neither in any body of
![]() $\mathit{hg}(\Sigma)$
nor in any head of
$\mathit{hg}(\Sigma)$
nor in any head of
![]() $\mathit{main}(\Sigma)$
.
$\mathit{main}(\Sigma)$
.
Algorithm 3: CertEval[Dyadic-![]() $_\mathcal{C}$](q, D, Σ, c)
$_\mathcal{C}$](q, D, Σ, c)

Concerning the equivalence between
![]() $\Sigma_\mathrm{HG} \cup \Sigma_\mathcal{C}$
and
$\Sigma_\mathrm{HG} \cup \Sigma_\mathcal{C}$
and
![]() $\Sigma$
, we can observe that it easily comes from the shape of
$\Sigma$
, we can observe that it easily comes from the shape of
![]() $\mathit{hg}(\sigma)$
and
$\mathit{hg}(\sigma)$
and
![]() $\mathit{main}(\sigma)$
with respect to each original rule
$\mathit{main}(\sigma)$
with respect to each original rule
![]() $\sigma \in \Sigma$
. Indeed, first, the body of
$\sigma \in \Sigma$
. Indeed, first, the body of
![]() $\sigma$
is first partitioned in
$\sigma$
is first partitioned in
![]() ${{\mathit{s}\textrm{-}\mathit{atoms}}}(\sigma)$
and
${{\mathit{s}\textrm{-}\mathit{atoms}}}(\sigma)$
and
![]() ${{\mathit{p}\textrm{-}\mathit{atoms}}}(\sigma)$
. Second, all the atoms if
${{\mathit{p}\textrm{-}\mathit{atoms}}}(\sigma)$
. Second, all the atoms if
![]() ${{\mathit{s}\textrm{-}\mathit{atoms}}}(\sigma)$
form the body of
${{\mathit{s}\textrm{-}\mathit{atoms}}}(\sigma)$
form the body of
![]() $\mathit{hg}(\sigma)$
. Then, all the variables of
$\mathit{hg}(\sigma)$
. Then, all the variables of
![]() $\mathit{hg}(\sigma)$
that are in join with
$\mathit{hg}(\sigma)$
that are in join with
![]() ${{\mathit{p}\textrm{-}\mathit{atoms}}}(\sigma)$
or are in the head of
${{\mathit{p}\textrm{-}\mathit{atoms}}}(\sigma)$
or are in the head of
![]() $\sigma$
are collected in
$\sigma$
are collected in
![]() $\mathtt{Aux}_{\sigma}(\mathit{vars}_\star(\sigma))$
. Finally,
$\mathtt{Aux}_{\sigma}(\mathit{vars}_\star(\sigma))$
. Finally,
![]() $\mathtt{Aux}_{\sigma}(\mathit{vars}_\star(\sigma))$
is put in conjunction with
$\mathtt{Aux}_{\sigma}(\mathit{vars}_\star(\sigma))$
is put in conjunction with
![]() ${{\mathit{p}\textrm{-}\mathit{atoms}}}(\sigma)$
to form the body of
${{\mathit{p}\textrm{-}\mathit{atoms}}}(\sigma)$
to form the body of
![]() $\mathit{main}(\sigma)$
. Such a way of decomposing a rule
$\mathit{main}(\sigma)$
. Such a way of decomposing a rule
![]() $\sigma$
is well-known to be correct for query answering purposes even when the variables in the auxiliary atom are harmful.
$\sigma$
is well-known to be correct for query answering purposes even when the variables in the auxiliary atom are harmful.
It remains to show that
![]() ${{\textsf{Dyadic-}\mathcal{C}}}$
is decidable. We rely on Algorithm 3 together with Theorem 1 and Proposition 4 to state the following result.
${{\textsf{Dyadic-}\mathcal{C}}}$
is decidable. We rely on Algorithm 3 together with Theorem 1 and Proposition 4 to state the following result.
Theorem 5 Consider a decidable class
![]() ${{\mathcal{C}}}$
of TGDs. Then,
${{\mathcal{C}}}$
of TGDs. Then,
![]() ${{cert-eval[{{\textsf{Dyadic-}\mathcal{C}}}]}}$
is decidable.
${{cert-eval[{{\textsf{Dyadic-}\mathcal{C}}}]}}$
is decidable.
Proof. To prove the statement we provide the terminating Algorithm 3. Let
![]() $\Sigma \in {{\textsf{Dyadic-}\mathcal{C}}}$
an ontology. Instructions 1 and 2 of the algorithm are introduced in order to construct the components
$\Sigma \in {{\textsf{Dyadic-}\mathcal{C}}}$
an ontology. Instructions 1 and 2 of the algorithm are introduced in order to construct the components
![]() $(\mathit{hg}(\Sigma), \mathit{main}(\Sigma))$
of a dyadic pair
$(\mathit{hg}(\Sigma), \mathit{main}(\Sigma))$
of a dyadic pair
![]() $\Pi$
, which is successively initialized at instruction 3. Of course, the construction of
$\Pi$
, which is successively initialized at instruction 3. Of course, the construction of
![]() $\Pi$
is based on a polynomial procedure with respect to the size of the input
$\Pi$
is based on a polynomial procedure with respect to the size of the input
![]() $\Sigma$
, hence these instructions always terminates. Finally, instruction 4 returns the result of the evaluation of the problem dp-cert-eval
$\Sigma$
, hence these instructions always terminates. Finally, instruction 4 returns the result of the evaluation of the problem dp-cert-eval
![]() ${{[{{\mathcal{C}}}]}}$
. To solve the latter, is invoked Algorithm 1, which in turn invokes Algorithm 2; their correctness is guaranteed by Theorem 1 and Proposition 4, respectively. Accordingly,
${{[{{\mathcal{C}}}]}}$
. To solve the latter, is invoked Algorithm 1, which in turn invokes Algorithm 2; their correctness is guaranteed by Theorem 1 and Proposition 4, respectively. Accordingly,
![]() ${{cert-eval[{{\textsf{Dyadic-}\mathcal{C}}}]}}$
is decidable.
${{cert-eval[{{\textsf{Dyadic-}\mathcal{C}}}]}}$
is decidable.
Finally, we conclude the section by proving that, for any class
![]() ${{\mathcal{C}}}$
including the class Af-Inds defined in Section 3.3, the class
${{\mathcal{C}}}$
including the class Af-Inds defined in Section 3.3, the class
![]() ${{\textsf{Dyadic-}\mathcal{C}}}$
includes Datalog.
${{\textsf{Dyadic-}\mathcal{C}}}$
includes Datalog.
Theorem 6 Consider a class
![]() ${{\mathcal{C}}}$
of TGDs. If
${{\mathcal{C}}}$
of TGDs. If
![]() ${{\mathcal{C}}} \supseteq {{\textsf{Af-Inds}}}$
, then
${{\mathcal{C}}} \supseteq {{\textsf{Af-Inds}}}$
, then
![]() ${{\textsf{Datalog}}} \subseteq {{\textsf{Dyadic-}\mathcal{C}}}$
.
${{\textsf{Datalog}}} \subseteq {{\textsf{Dyadic-}\mathcal{C}}}$
.
Proof. Consider a datalog rule
![]() $\sigma: \Phi(\mathbf{x,y}) \rightarrow P(\mathbf{x})$
. Then, it can be decomposed into the following two rules:
$\sigma: \Phi(\mathbf{x,y}) \rightarrow P(\mathbf{x})$
. Then, it can be decomposed into the following two rules:
![]() $\mathit{hg}(\sigma): \Phi(\mathbf{x,y}) \rightarrow \mathtt{Aux}_\sigma(\mathbf{x})$
and
$\mathit{hg}(\sigma): \Phi(\mathbf{x,y}) \rightarrow \mathtt{Aux}_\sigma(\mathbf{x})$
and
![]() $\mathit{main}(\sigma): \mathtt{Aux}_\sigma(\mathbf{x}) \rightarrow P(\mathbf{x})$
. Trivially,
$\mathit{main}(\sigma): \mathtt{Aux}_\sigma(\mathbf{x}) \rightarrow P(\mathbf{x})$
. Trivially,
![]() $\mathit{hg}(\sigma) \in \Sigma_\mathrm{HG}$
; it remains to show that
$\mathit{hg}(\sigma) \in \Sigma_\mathrm{HG}$
; it remains to show that
![]() $\mathit{main}(\sigma) \in {{\textsf{Af-Inds}}}$
. According to Definition 3, the full property immediately follows since datalog rules do no have existential variables, whereas the autonomous property holds since
$\mathit{main}(\sigma) \in {{\textsf{Af-Inds}}}$
. According to Definition 3, the full property immediately follows since datalog rules do no have existential variables, whereas the autonomous property holds since
![]() $\mathit{body}(\mathit{main}(\sigma))$
contains only the fresh predicate
$\mathit{body}(\mathit{main}(\sigma))$
contains only the fresh predicate
![]() $\mathtt{H}$
. In particular,
$\mathtt{H}$
. In particular,
![]() $\mathit{main}(\sigma) \in {{\mathcal{C}}}$
, since by assumption
$\mathit{main}(\sigma) \in {{\mathcal{C}}}$
, since by assumption
![]() ${{\mathcal{C}}} \supseteq {{\textsf{Af-Inds}}}$
; hence, the thesis follows.
${{\mathcal{C}}} \supseteq {{\textsf{Af-Inds}}}$
; hence, the thesis follows.
6 Computational complexity of query answering
In this section we study the complexity of the
![]() ${{cert-eval}}$
problem over dyadic existential rules. We start analyzing the data complexity of the problem and then the combined complexity.
${{cert-eval}}$
problem over dyadic existential rules. We start analyzing the data complexity of the problem and then the combined complexity.
Theorem 7 Consider a class
![]() ${{\mathcal{C}}}$
of TGDs. In data complexity, if cert-eval
${{\mathcal{C}}}$
of TGDs. In data complexity, if cert-eval
![]() ${{[{{\mathcal{C}}}]}}$
belongs to some decidable complexity class
${{[{{\mathcal{C}}}]}}$
belongs to some decidable complexity class
![]() $\mathbb{C}$
, then the following hold:
$\mathbb{C}$
, then the following hold:
1. If
 $\mathbb{C} \subseteq { \textbf{PTIME}}$
, then
$\mathbb{C} \subseteq { \textbf{PTIME}}$
, then
 ${{cert-eval[{{\textsf{Dyadic-}\mathcal{C}}}]}}$
is in PTIME;
${{cert-eval[{{\textsf{Dyadic-}\mathcal{C}}}]}}$
is in PTIME;-
2. If
 $\mathbb{C} \supseteq { \textbf{PTIME}}$
, then
$\mathbb{C} \supseteq { \textbf{PTIME}}$
, then
 ${{cert-eval[{{\textsf{Dyadic-}\mathcal{C}}}]}}$
is in
${{cert-eval[{{\textsf{Dyadic-}\mathcal{C}}}]}}$
is in
 ${ \textbf{PTIME}}^{\mathbb{C}}$
;
${ \textbf{PTIME}}^{\mathbb{C}}$
; 3. If
 $\mathbb{C} \supseteq { \textbf{PTIME}}$
is deterministic Footnote 2 and cert-eval
$\mathbb{C} \supseteq { \textbf{PTIME}}$
is deterministic Footnote 2 and cert-eval
 ${{[{{\mathcal{C}}}]}}$
is
${{[{{\mathcal{C}}}]}}$
is
 $\mathbb{C}$
-complete, then it holds that
$\mathbb{C}$
-complete, then it holds that
 ${{cert-eval[{{\textsf{Dyadic-}\mathcal{C}}}]}}$
is
${{cert-eval[{{\textsf{Dyadic-}\mathcal{C}}}]}}$
is
 $\mathbb{C}$
-complete too;
$\mathbb{C}$
-complete too;4. If
 $\mathcal{C} \supseteq {{\textsf{Af-Inds}}}$
, then
$\mathcal{C} \supseteq {{\textsf{Af-Inds}}}$
, then
 ${{cert-eval[{{\textsf{Dyadic-}\mathcal{C}}}]}}$
is
${{cert-eval[{{\textsf{Dyadic-}\mathcal{C}}}]}}$
is
 ${{{ \textbf{PTIME}}{\textrm{-hard}}}}$
.
${{{ \textbf{PTIME}}{\textrm{-hard}}}}$
.
Proof. To prove the theorem, we rely on the complexity of Algorithm 3. Let D be a database,
![]() $\Sigma \in {{\textsf{Dyadic-}\mathcal{C}}}$
an ontology,
$\Sigma \in {{\textsf{Dyadic-}\mathcal{C}}}$
an ontology,
![]() $q(\mathbf{x})$
a CQ, and
$q(\mathbf{x})$
a CQ, and
![]() $\mathbf{c} \in \mathsf{C}^{|\mathbf{x}|}$
a tuple. Moreover, let
$\mathbf{c} \in \mathsf{C}^{|\mathbf{x}|}$
a tuple. Moreover, let
![]() $d = |\mathit{consts}(D)|$
and
$d = |\mathit{consts}(D)|$
and
![]() $\mu = \max_{P \in \mathit{h}\textrm{-}\mathit{preds}(\Sigma_\mathrm{HG})} \mathit{arity}(P)$
. As shown in Theorem 5, Algorithm 3 terminates and correctly decides
$\mu = \max_{P \in \mathit{h}\textrm{-}\mathit{preds}(\Sigma_\mathrm{HG})} \mathit{arity}(P)$
. As shown in Theorem 5, Algorithm 3 terminates and correctly decides
![]() ${{cert-eval[{{\textsf{Dyadic-}\mathcal{C}}}]}}$
. More specifically, instructions 1 and 2 are introduced in order to construct, respectively, the first component
${{cert-eval[{{\textsf{Dyadic-}\mathcal{C}}}]}}$
. More specifically, instructions 1 and 2 are introduced in order to construct, respectively, the first component
![]() $\mathit{hg}(\Sigma)$
and the second component
$\mathit{hg}(\Sigma)$
and the second component
![]() $\mathit{main}(\Sigma)$
of a dyadic pair. The procedure used to build these sets is polynomial (indeed linear) with respect to the size of the ontology
$\mathit{main}(\Sigma)$
of a dyadic pair. The procedure used to build these sets is polynomial (indeed linear) with respect to the size of the ontology
![]() $\Sigma$
in input. By neglecting the “trivial" instruction 3, the computational cost of the Algorithm mainly depends on instruction 4, that is on the invocation of Algorithm 2, which in turn invokes Algorithm 2 in order to compute the completed database
$\Sigma$
in input. By neglecting the “trivial" instruction 3, the computational cost of the Algorithm mainly depends on instruction 4, that is on the invocation of Algorithm 2, which in turn invokes Algorithm 2 in order to compute the completed database
![]() $D^+$
. As stated in Proposition 4, Algorithm 2 always terminates. In particular, the size of the set
$D^+$
. As stated in Proposition 4, Algorithm 2 always terminates. In particular, the size of the set
![]() $D^+$
is at most
$D^+$
is at most
![]() $|\mathit{h}\textrm{-}\mathit{preds}(\Sigma_\mathrm{HG})| \cdot d^{\mu}$
; the problem cert-eval
$|\mathit{h}\textrm{-}\mathit{preds}(\Sigma_\mathrm{HG})| \cdot d^{\mu}$
; the problem cert-eval
![]() ${{[{{\mathcal{C}}}]}}$
, at instruction 5, is called
${{[{{\mathcal{C}}}]}}$
, at instruction 5, is called
![]() $d^{\mu}$
times, and the for-loop at instruction 3 is executed
$d^{\mu}$
times, and the for-loop at instruction 3 is executed
![]() $|\Sigma_\mathrm{HG}|$
times. Therefore, by ignoring the computational costs of the oracle (i.e., checking whether
$|\Sigma_\mathrm{HG}|$
times. Therefore, by ignoring the computational costs of the oracle (i.e., checking whether
![]() $\mathbf{t} \in \mathit{cert}(q,D^+,\Sigma_\mathcal{C})$
), Algorithm 2 overall performs a number of step that is linear in
$\mathbf{t} \in \mathit{cert}(q,D^+,\Sigma_\mathcal{C})$
), Algorithm 2 overall performs a number of step that is linear in
![]() $|\Sigma_\mathrm{HG}| \cdot |\mathit{h}\textrm{-}\mathit{preds}(\Sigma_\mathrm{HG})| \cdot d^{2\mu}$
. Indeed, this value is also an upper bound for the number of calls to the oracle. Since we are in data complexity, the following parameters are bounded: the maximum arity
$|\Sigma_\mathrm{HG}| \cdot |\mathit{h}\textrm{-}\mathit{preds}(\Sigma_\mathrm{HG})| \cdot d^{2\mu}$
. Indeed, this value is also an upper bound for the number of calls to the oracle. Since we are in data complexity, the following parameters are bounded: the maximum arity
![]() $\mu$
, the size of the sets
$\mu$
, the size of the sets
![]() $\Sigma_\mathrm{HG}$
and
$\Sigma_\mathrm{HG}$
and
![]() $\Sigma_\mathcal{C}$
, as well as the size and the number of each query q constructed at instruction 4 of Algorithm 2. Hence, the latter calls polynomially many times the problem cert-eval
$\Sigma_\mathcal{C}$
, as well as the size and the number of each query q constructed at instruction 4 of Algorithm 2. Hence, the latter calls polynomially many times the problem cert-eval
![]() ${{[{{\mathcal{C}}}]}}$
. Accordingly, Algorithm 3 is polynomial and in turn it invokes polynomially many times an oracle to compute cert-eval
${{[{{\mathcal{C}}}]}}$
. Accordingly, Algorithm 3 is polynomial and in turn it invokes polynomially many times an oracle to compute cert-eval
![]() ${{[{{\mathcal{C}}}]}}$
. Hence, if
${{[{{\mathcal{C}}}]}}$
. Hence, if
![]() $\mathbb{C} \subseteq { \textbf{PTIME}}$
, trivially
$\mathbb{C} \subseteq { \textbf{PTIME}}$
, trivially
![]() ${{cert-eval[{{\textsf{Dyadic-}\mathcal{C}}}]}} \in { \textbf{PTIME}}$
; whereas, if
${{cert-eval[{{\textsf{Dyadic-}\mathcal{C}}}]}} \in { \textbf{PTIME}}$
; whereas, if
![]() $\mathbb{C} \supseteq { \textbf{PTIME}}$
,
$\mathbb{C} \supseteq { \textbf{PTIME}}$
,
![]() ${{cert-eval[{{\textsf{Dyadic-}\mathcal{C}}}]}} \in { \textbf{PTIME}}^{\mathbb{C}}$
. To prove point 3 of the theorem, we observe that the membership follows from point 2 and from the fact that, for any deterministic class
${{cert-eval[{{\textsf{Dyadic-}\mathcal{C}}}]}} \in { \textbf{PTIME}}^{\mathbb{C}}$
. To prove point 3 of the theorem, we observe that the membership follows from point 2 and from the fact that, for any deterministic class
![]() $\mathbb{C} \supseteq { \textbf{PTIME}}$
, it holds that
$\mathbb{C} \supseteq { \textbf{PTIME}}$
, it holds that
![]() ${ \textbf{PTIME}}^{\mathbb{C}} = \mathbb{C}$
; whereas, the hardness derives from Proposition 5, since
${ \textbf{PTIME}}^{\mathbb{C}} = \mathbb{C}$
; whereas, the hardness derives from Proposition 5, since
![]() ${{\textsf{Dyadic-}\mathcal{C}}}$
includes the class
${{\textsf{Dyadic-}\mathcal{C}}}$
includes the class
![]() ${{\mathcal{C}}}$
, that is
${{\mathcal{C}}}$
, that is
![]() $\mathbb{C}$
-hard by assumption. Finally, to prove point 4, we recall that by Theorem 6,
$\mathbb{C}$
-hard by assumption. Finally, to prove point 4, we recall that by Theorem 6,
![]() ${{\textsf{Datalog}}} \subseteq {{\textsf{Dyadic-}\mathcal{C}}}$
; hence, since
${{\textsf{Datalog}}} \subseteq {{\textsf{Dyadic-}\mathcal{C}}}$
; hence, since
![]() ${{cert-eval}}[{{\textsf{Datalog}}}]$
is
${{cert-eval}}[{{\textsf{Datalog}}}]$
is
![]() ${{{ \textbf{PTIME}}{\textrm{-hard}}}}$
, the thesis follows.
${{{ \textbf{PTIME}}{\textrm{-hard}}}}$
, the thesis follows.
Accordingly to the above theorem, immediately we get the following result.
Corollary 1 Complexity results in Table 2 do hold.
Table 2. Data complexity comparison of cert-eval
![]() ${{[{{\mathcal{C}}}]}}$
with
${{[{{\mathcal{C}}}]}}$
with
![]() ${{cert-eval[{{\textsf{Dyadic-}\mathcal{C}}}]}}$
${{cert-eval[{{\textsf{Dyadic-}\mathcal{C}}}]}}$

For studying the combined complexity, we need to take into account the fact that the database returned by Algorithm 2 (namely,
![]() $D^+$
) is exponential with respect to the input one (namely, D). Indeed, the check
$D^+$
) is exponential with respect to the input one (namely, D). Indeed, the check
![]() $\mathbf{c} \in \mathit{cert}(q,D^+,\Sigma_\mathcal{C})$
performed by Algorithm 1 is done on an exponentially bigger database. Thus, in case cert-eval
$\mathbf{c} \in \mathit{cert}(q,D^+,\Sigma_\mathcal{C})$
performed by Algorithm 1 is done on an exponentially bigger database. Thus, in case cert-eval
![]() ${{[{{\mathcal{C}}}]}}$
would have the same data complexity and combined complexity, it might happen that the combined complexity of
${{[{{\mathcal{C}}}]}}$
would have the same data complexity and combined complexity, it might happen that the combined complexity of
![]() ${{cert-eval[{{\textsf{Dyadic-}\mathcal{C}}}]}}$
could be exponentially higher that the one of cert-eval
${{cert-eval[{{\textsf{Dyadic-}\mathcal{C}}}]}}$
could be exponentially higher that the one of cert-eval
![]() ${{[{{\mathcal{C}}}]}}$
. Although all the considered classes in
${{[{{\mathcal{C}}}]}}$
. Although all the considered classes in
![]() $\mathbb{E}^+_{\mathit{syn}}$
do not suffer from this shortcoming, before stating our general result, we need to focus on “well-behaved” classes of TGDs. A class
$\mathbb{E}^+_{\mathit{syn}}$
do not suffer from this shortcoming, before stating our general result, we need to focus on “well-behaved” classes of TGDs. A class
![]() ${{\mathcal{C}}}$
of TGDs enjoys the dropping data-complexity property if there is an exponential jump from the combined complexity of cert-eval
${{\mathcal{C}}}$
of TGDs enjoys the dropping data-complexity property if there is an exponential jump from the combined complexity of cert-eval
![]() ${{[{{\mathcal{C}}}]}}$
to the data complexity of cert-eval
${{[{{\mathcal{C}}}]}}$
to the data complexity of cert-eval
![]() ${{[{{\mathcal{C}}}]}}$
.
${{[{{\mathcal{C}}}]}}$
.
Proposition 6 Each class in
![]() $\mathbb{E}_{\mathit{syn}}$
enjoys the dropping data-complexity property.
$\mathbb{E}_{\mathit{syn}}$
enjoys the dropping data-complexity property.
We can now state the last result of the section, providing the combined complexity of problem
![]() ${{cert-eval}}$
over
${{cert-eval}}$
over
![]() ${{\textsf{Dyadic-}\mathcal{C}}}$
sets of TGDs.
${{\textsf{Dyadic-}\mathcal{C}}}$
sets of TGDs.
Theorem 8 Consider a class
![]() ${{\mathcal{C}}}$
of TGDs. In combined complexity, if cert-eval
${{\mathcal{C}}}$
of TGDs. In combined complexity, if cert-eval
![]() ${{[{{\mathcal{C}}}]}}$
belongs to some decidable complexity class
${{[{{\mathcal{C}}}]}}$
belongs to some decidable complexity class
![]() $\mathbb{C}$
and
$\mathbb{C}$
and
![]() ${{\mathcal{C}}}$
enjoys the dropping data-complexity property, then the following hold:
${{\mathcal{C}}}$
enjoys the dropping data-complexity property, then the following hold:
1. If
 $\mathbb{C} \subseteq { \textbf{EXPTIME}}$
, then
$\mathbb{C} \subseteq { \textbf{EXPTIME}}$
, then
 ${{cert-eval[{{\textsf{Dyadic-}\mathcal{C}}}]}}$
is in EXPTIME;
${{cert-eval[{{\textsf{Dyadic-}\mathcal{C}}}]}}$
is in EXPTIME;2. If
 $\mathbb{C} \supseteq { \textbf{EXPTIME}}$
, then
$\mathbb{C} \supseteq { \textbf{EXPTIME}}$
, then
 ${{cert-eval[{{\textsf{Dyadic-}\mathcal{C}}}]}}$
is in
${{cert-eval[{{\textsf{Dyadic-}\mathcal{C}}}]}}$
is in
 ${ \textbf{EXPTIME}}^{\mathbb{C}}$
;
${ \textbf{EXPTIME}}^{\mathbb{C}}$
;3. If
 $\mathbb{C} \supseteq { \textbf{EXPTIME}}$
is deterministic and cert-eval
$\mathbb{C} \supseteq { \textbf{EXPTIME}}$
is deterministic and cert-eval
 ${{[{{\mathcal{C}}}]}}$
is
${{[{{\mathcal{C}}}]}}$
is
 $\mathbb{C}$
-complete, then it holds that
$\mathbb{C}$
-complete, then it holds that
 ${{cert-eval[{{\textsf{Dyadic-}\mathcal{C}}}]}}$
is
${{cert-eval[{{\textsf{Dyadic-}\mathcal{C}}}]}}$
is
 $\mathbb{C}$
-complete too;
$\mathbb{C}$
-complete too;4. If
 $\mathcal{C} \supseteq {{\textsf{Af-Inds}}}$
, then
$\mathcal{C} \supseteq {{\textsf{Af-Inds}}}$
, then
 ${{cert-eval[{{\textsf{Dyadic-}\mathcal{C}}}]}}$
is EXPTIME-hard.
${{cert-eval[{{\textsf{Dyadic-}\mathcal{C}}}]}}$
is EXPTIME-hard.
Proof. The argument proceeds similarly to proof of Theorem 7 by arguing on Algorithm 3 to determine the complexity of
![]() ${{cert-eval[{{\textsf{Dyadic-}\mathcal{C}}}]}}$
. Let D be a database,
${{cert-eval[{{\textsf{Dyadic-}\mathcal{C}}}]}}$
. Let D be a database,
![]() $\Sigma \in {{\textsf{Dyadic-}\mathcal{C}}}$
an ontology,
$\Sigma \in {{\textsf{Dyadic-}\mathcal{C}}}$
an ontology,
![]() $q(\mathbf{x})$
a CQ, and
$q(\mathbf{x})$
a CQ, and
![]() $\mathbf{c} \in \mathsf{C}^{|\mathbf{x}|}$
a tuple. Moreover, let
$\mathbf{c} \in \mathsf{C}^{|\mathbf{x}|}$
a tuple. Moreover, let
![]() $d = |\mathit{consts}(D)|$
and
$d = |\mathit{consts}(D)|$
and
![]() $\mu = \max_{P \in \mathit{h}\textrm{-}\mathit{preds}(\Sigma_\mathrm{HG})} \mathit{arity}(P)$
. As previously shown, Algorithm 3 invokes Algorithm 1, which in turn invokes Algorithm 2. Concerning the latter, by ignoring the computational costs of the oracle, it overall performs a number of step that is linear in
$\mu = \max_{P \in \mathit{h}\textrm{-}\mathit{preds}(\Sigma_\mathrm{HG})} \mathit{arity}(P)$
. As previously shown, Algorithm 3 invokes Algorithm 1, which in turn invokes Algorithm 2. Concerning the latter, by ignoring the computational costs of the oracle, it overall performs a number of step that is linear in
![]() $|\Sigma_\mathrm{HG}| \cdot |\mathit{h}\textrm{-}\mathit{preds}(\Sigma_\mathrm{HG})| \cdot d^{2\mu}$
. Indeed, also in this case, this value is an upper bound for the number of calls to the oracle. This is enough to show point 2.
$|\Sigma_\mathrm{HG}| \cdot |\mathit{h}\textrm{-}\mathit{preds}(\Sigma_\mathrm{HG})| \cdot d^{2\mu}$
. Indeed, also in this case, this value is an upper bound for the number of calls to the oracle. This is enough to show point 2.
Concerning the memberships of point 1 and point 3, differently from the proof of Theorem 7, in combined complexity the maximum arity
![]() $\mu$
, the size of the sets
$\mu$
, the size of the sets
![]() $\Sigma_\mathrm{HG}$
and
$\Sigma_\mathrm{HG}$
and
![]() $\Sigma_\mathcal{C}$
, as well as the size and the number of each query constructed at instruction 4 of Algorithm 2 are not bounded. Accordingly, also the size of the completed database returned by Algorithm 2 (namely
$\Sigma_\mathcal{C}$
, as well as the size and the number of each query constructed at instruction 4 of Algorithm 2 are not bounded. Accordingly, also the size of the completed database returned by Algorithm 2 (namely
![]() $D^+$
) may become exponential with respect to the input. More precisely,
$D^+$
) may become exponential with respect to the input. More precisely,
![]() $|\mathit{consts}(D^+)| = d$
and
$|\mathit{consts}(D^+)| = d$
and
![]() $|D^+| \leq |\mathit{h}\textrm{-}\mathit{preds}(\Sigma_\mathrm{HG})|\cdot d^\mu + |D|$
. Let n generically denote the size
$|D^+| \leq |\mathit{h}\textrm{-}\mathit{preds}(\Sigma_\mathrm{HG})|\cdot d^\mu + |D|$
. Let n generically denote the size
![]() $||seq||$
of any sequence
$||seq||$
of any sequence
![]() $\mathit{seq}$
of objects given in input to cert-eval
$\mathit{seq}$
of objects given in input to cert-eval
![]() ${{[{{\mathcal{C}}}]}}$
. We can now consider the cost function g(n) (resp., f(n)) of some algorithm/oracle that decides cert-eval
${{[{{\mathcal{C}}}]}}$
. We can now consider the cost function g(n) (resp., f(n)) of some algorithm/oracle that decides cert-eval
![]() ${{[{{\mathcal{C}}}]}}$
and shows that it belongs to
${{[{{\mathcal{C}}}]}}$
and shows that it belongs to
![]() $\mathbb{C}$
(resp.,
$\mathbb{C}$
(resp.,
![]() $\mathbb{C}_d$
) in combined (resp., data) complexity. According to the dropping data-complexity property, we know that g(n) grows at least exponentially faster than f(n). Essentially, there is an exponential jump from
$\mathbb{C}_d$
) in combined (resp., data) complexity. According to the dropping data-complexity property, we know that g(n) grows at least exponentially faster than f(n). Essentially, there is an exponential jump from
![]() $\mathbb{C}_d$
to
$\mathbb{C}_d$
to
![]() $\mathbb{C}$
that does not depend on the size of the input database but only on the size of other parameters, namely the ontology, the query, and the tuple of constants. Consider now the query
$\mathbb{C}$
that does not depend on the size of the input database but only on the size of other parameters, namely the ontology, the query, and the tuple of constants. Consider now the query
![]() $q':= \langle \mathbf{x} \rangle \leftarrow \Phi(\mathbf{x,y})$
constructed at instruction 4 of Algorithm 2 (we call it q’ to avoid confusion with
$q':= \langle \mathbf{x} \rangle \leftarrow \Phi(\mathbf{x,y})$
constructed at instruction 4 of Algorithm 2 (we call it q’ to avoid confusion with
![]() $q(\mathbf{x})$
mentioned at the beginning of this proof). At instruction 5 of the same algorithm, the oracle for cert-eval
$q(\mathbf{x})$
mentioned at the beginning of this proof). At instruction 5 of the same algorithm, the oracle for cert-eval
![]() ${{[{{\mathcal{C}}}]}}$
checks whether
${{[{{\mathcal{C}}}]}}$
checks whether
![]() $\mathbf{t} \in \mathit{cert}(q',D^+,\Sigma_\mathcal{C})$
holds. Since g(n) grows at least exponentially faster than f(n), we get that
$\mathbf{t} \in \mathit{cert}(q',D^+,\Sigma_\mathcal{C})$
holds. Since g(n) grows at least exponentially faster than f(n), we get that
![]() $g(||\mathbf{t},q',D^+,\Sigma_\mathcal{C}||)$
remains of the same exponential order of
$g(||\mathbf{t},q',D^+,\Sigma_\mathcal{C}||)$
remains of the same exponential order of
![]() $g(||\mathbf{t},q',D,\Sigma_\mathcal{C}||)$
, although
$g(||\mathbf{t},q',D,\Sigma_\mathcal{C}||)$
, although
![]() $||D^+||$
may be exponentially larger than
$||D^+||$
may be exponentially larger than
![]() $||D||$
.
$||D||$
.
Regarding point 1, if
![]() $\mathbb{C} \subseteq { \textbf{EXPTIME}}$
, then we know that a
$\mathbb{C} \subseteq { \textbf{EXPTIME}}$
, then we know that a
![]() $\mathbb{C}$
-oracle for cert-eval
$\mathbb{C}$
-oracle for cert-eval
![]() ${{[{{\mathcal{C}}}]}}$
works at most exponentially in
${{[{{\mathcal{C}}}]}}$
works at most exponentially in
![]() $||\mathbf{t},q',\Sigma_\mathcal{C}||$
and at most polynomially (resp., exponentially) in
$||\mathbf{t},q',\Sigma_\mathcal{C}||$
and at most polynomially (resp., exponentially) in
![]() $||D^+||$
(resp.,
$||D^+||$
(resp.,
![]() $||D||$
); thus, in this case, the
$||D||$
); thus, in this case, the
![]() $\mathbb{C}$
-oracle cannot reach double-exponential time but it remains exponential. Therefore,
$\mathbb{C}$
-oracle cannot reach double-exponential time but it remains exponential. Therefore,
![]() ${{cert-eval[{{\textsf{Dyadic-}\mathcal{C}}}]}} \in { \textbf{EXPTIME}}$
.
${{cert-eval[{{\textsf{Dyadic-}\mathcal{C}}}]}} \in { \textbf{EXPTIME}}$
.
For the memberships of point 3, we already know that
![]() ${{cert-eval[{{\textsf{Dyadic-}\mathcal{C}}}]}}$
is in
${{cert-eval[{{\textsf{Dyadic-}\mathcal{C}}}]}}$
is in
![]() ${ \textbf{EXPTIME}}^{\mathbb{C}}$
. Consider now a
${ \textbf{EXPTIME}}^{\mathbb{C}}$
. Consider now a
![]() $\mathbb{C}$
-oracle O for cert-eval
$\mathbb{C}$
-oracle O for cert-eval
![]() ${{[{{\mathcal{C}}}]}}$
characterized by the cost function g(n). If
${{[{{\mathcal{C}}}]}}$
characterized by the cost function g(n). If
![]() $\mathbb{C} \supseteq { \textbf{EXPTIME}}$
is deterministic, then O works with respect to
$\mathbb{C} \supseteq { \textbf{EXPTIME}}$
is deterministic, then O works with respect to
![]() $||\mathbf{t},q',\Sigma_\mathcal{C}||$
in an exponentially faster way than with respect to
$||\mathbf{t},q',\Sigma_\mathcal{C}||$
in an exponentially faster way than with respect to
![]() $||D^+||$
; thus, also in this case, O cannot exceed the power of
$||D^+||$
; thus, also in this case, O cannot exceed the power of
![]() $\mathbb{C}$
. Therefore,
$\mathbb{C}$
. Therefore,
![]() ${ \textbf{EXPTIME}}^{\mathbb{C}}$
, in a sense, collapses to
${ \textbf{EXPTIME}}^{\mathbb{C}}$
, in a sense, collapses to
![]() $ \mathbb{C}$
.
$ \mathbb{C}$
.
Finally, we conclude the proof by considering the hardness of points 3 and 4. In the first case, we observe that it derives from Proposition 5, since
![]() ${{\textsf{Dyadic-}\mathcal{C}}}$
includes the class
${{\textsf{Dyadic-}\mathcal{C}}}$
includes the class
![]() ${{\mathcal{C}}}$
, that is
${{\mathcal{C}}}$
, that is
![]() $\mathbb{C}$
-hard by assumption. For point 4, we recall that by Theorem 6,
$\mathbb{C}$
-hard by assumption. For point 4, we recall that by Theorem 6,
![]() ${{\textsf{Datalog}}} \subseteq {{\textsf{Dyadic-}\mathcal{C}}}$
; hence, since
${{\textsf{Datalog}}} \subseteq {{\textsf{Dyadic-}\mathcal{C}}}$
; hence, since
![]() ${{cert-eval}}[{{\textsf{Datalog}}}]$
is
${{cert-eval}}[{{\textsf{Datalog}}}]$
is
![]() ${ \textbf{EXPTIME}}$
-hard, it follows the thesis.
${ \textbf{EXPTIME}}$
-hard, it follows the thesis.
The following immediately derives from above theorem.
Corollary 2 Complexity results in Table 3 do hold.
Table 3. Combined complexity comparison of cert-eval
![]() ${{[{{\mathcal{C}}}]}}$
with
${{[{{\mathcal{C}}}]}}$
with
![]() ${{cert-eval[{{\textsf{Dyadic-}\mathcal{C}}}]}}$
${{cert-eval[{{\textsf{Dyadic-}\mathcal{C}}}]}}$

7 Conclusion
Dyadic decomposable sets form a novel decidable class of TGDs that encompasses and generalizes all the existing (syntactic and semantic) decidable classes of TGDs. In the near feature, it would be interesting to implement a prototype for dyadic existential rules by exploiting different kinds of existing reasoners.
Acknowledgments
Georg Gottlob is a Royal Society Research Professor and acknowledges support by the Royal Society under this scheme (Project “RAISON DATA” RP/R1/201074). Marco Manna was partially supported by the PNRR projects “FAIR (PE00000013) - Spoke 9” and “Tech4You (ECS00000009) - Spoke 6”, under the NRRP MUR program funded by the NextGenerationEU. Cinzia Marte was partially supported by the PON project “Modelli, Sistemi e Competenze per l’Implementazione dell’Ufficio per il Processo - STARTUPP (H29J22000390006)”.