Hostname: page-component-848d4c4894-5nwft Total loading time: 0 Render date: 2024-06-11T02:07:58.577Z Has data issue: false hasContentIssue false
  • English
  • Français

On lower semicontinuity of a defect energy obtained by a singular limit of the Ginzburg–Landau type energy for gradient fields

Published online by Cambridge University Press:  14 November 2011

Patricio Aviles  and
Yoshikazu Giga
Patricio Aviles
Affiliation:
Department of Mathematics, Hokkaido University, Sapporo 060, Japan
Yoshikazu Giga
Affiliation:
Department of Mathematics, Hokkaido University, Sapporo 060, Japan
Get access Rights & Permissions [Opens in a new window]

Extract

A defect energy Jβ, which measures jump discontinuities of a unit length gradient field, is studied. The number β indicates the power of the jumps of the gradient fields that appear in the density of Jβ. It is shown that Jβ for β = 3 is lower semicontinuous (on the space of unit gradient fields belonging to BV) in L1-convergence of gradient fields. 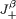A similar result holds for the modified energy , which measures only a particular type of defect. The result turns out to be very subtle, since 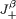with β > 3 is not lower semicontinuous, as is shown in this paper. The key idea behind semicontinuity is a duality representation for J3 and 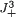. The duality representation is also important for obtaining a lower bound by using J3+ for the relaxation limit of the Ginzburg–Landau type energy for gradient fields. The lower bound obtained here agrees with the conjectured value of the relaxation limit.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 129 , Issue 1 , 1999 , pp. 1 - 17
Copyright
Copyright © Royal Society of Edinburgh 1999

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Alberti, G.. Rank one property for derivatives of functions with bounded variation. Proc. R. Soc. Edinb. A 123 (1993), 239–274.Google Scholar
2Aviles, P. and Giga, Y.. A mathematical problem related to the physical theory of liquid crystal configurations. Proc. Centre Math. Analysis Austral. Natn. Univ. 12 (1987), 1–16.Google Scholar
3Aviles, P. and Giga, Y.. Singularities and rank one properties of Hessian measures. Duke Math. J. 58 (1989), 441–467.CrossRefGoogle Scholar
4Aviles, P. and Giga, Y.. Variational integrals on mappings of bounded variation and their lower semicontinuity. Arch. Ration. Mech. Analysis 115 (1991), 201–255.Google Scholar
5Aviles, P. and Giga, Y.. Minimal currents, greodesic and relaxation of variational integrals on mappings of bounded variation. Duke Math. J. 67 (1992), 517–538.Google Scholar
6Aviles, P. and Giga, Y.. The distance function and defect energy. Proc. R. Soc. Edinb. A 126 (1996), 923–938.Google Scholar
7Maso, G. Dal. An introduction to Γ-convergence (Birkhäuser, 1993).Google Scholar
8Giorgi, E. De. Nuovi theremi relativi alle misure (r – 1)-dimensionale inn uno spazio ad r dimension. Ricerche Mat. 4 (1995), 95–113.Google Scholar
9De Giorgi, E.. G-operators and Γ-convergence. In Proc. ICM Poland 1983, Warszawa, vol. 2, pp. 1175–1191.Google Scholar
10Federer, H.. Geometric measure theory (Springer, 1969).Google Scholar
11Giusti, E.. Minimal surfaces and functions of bounded variations (Boston: Birkhäuser, 1984).CrossRefGoogle Scholar
12Jin, W. and Kohn, R.. (In preparation.) (Also see W. Jin, Singular perturbation and the energy of folds, PhD thesis (New York University, 1997).)Google Scholar
13Kohn, R. and Müller, S.. Relaxation and regularization of nonconvex variational problems. Rend. Semi. Mat. Fis. Univ. Milano 62 (1992), 89–113.Google Scholar
14Kohn, R. and Müller, S.. Surface energy and microstructure in coherent phase transition. Commun. Pure Appl. Math. 47 (1994), 405–435.Google Scholar
15Lions, P. L.. Generalized solutions of Hamilton–Jacobi equations. (Boston: Pitman Advanced Publishing Program, 1982).Google Scholar
16Modica, L.. The gradient theory of phase transitions and the minimal surface criterion. Arch. Ration. Mech. Analysis 98 (1987), 123–142.Google Scholar
17Ortiz, M. and Gioia, G.. The morphology and folding patterns of bucking driven thin-film filters. J. Mech. Phys. Solids 42 (1994), 531–559.Google Scholar
18Sethna, J. and Kleman, M.. Spheric domains in smectic liquid crystals. Phys. Rev. A 26 (1982), 3037–3040.CrossRefGoogle Scholar
19Simon, L.. Lectures on geometric measure theory. Proc. Centre Math. Analysis Austral. Natn. Univ. 3 (1983).Google Scholar
20Sternberg, P.. The effect of a singular perturbation on nonconvex variational problems. Arch. Ration. Mech. Analysis 101 (1988), 209–260.Google Scholar
21Vol'pert, A. I.. The spaces BV and quasilinear equations. Math. USSR. Sbornik 2 (1967), 225–267.CrossRefGoogle Scholar
22Berg, H. A. M. van den. Self-consistent domain theory in soft-ferromagnetic media. II. Basic domain structure in thin film objects. J. Appl. Phys. 60 (1986) 1104–1113.Google Scholar
23Berg, H. A. M. van den and Brandt, A. H. J. van den. Self-consistent domain theory in soft-ferromagnetic media. III. Composite structures in thin-film objects. J. Appl. Phys. 62 (1987), 1952–1959.Google Scholar