Hostname: page-component-848d4c4894-ttngx Total loading time: 0 Render date: 2024-05-16T11:57:05.046Z Has data issue: false hasContentIssue false
  • English
  • Français

Reliability analyses of linear two-dimensional consecutive k-type systems

Part of: Stochastic processes Operations research and management science

Published online by Cambridge University Press:  14 August 2023

He Yi ,
Narayanaswamy Balakrishnan  and
Xiang Li
He Yi*
Affiliation:
Beijing University of Chemical Technology
Narayanaswamy Balakrishnan*
Affiliation:
McMaster University
Xiang Li*
Affiliation:
Beijing University of Chemical Technology
*
*Postal address: School of Economics and Management, Beijing University of Chemical Technology, Beijing, 100029, China.
***Postal address: Department of Mathematics and Statistics, McMaster University, Hamilton, Ontario L8S 4K1, Canada.
*Postal address: School of Economics and Management, Beijing University of Chemical Technology, Beijing, 100029, China.
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, several linear two-dimensional consecutive k-type systems are studied, which include the linear connected-(k, r)-out-of-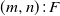$(m,n)\colon\! F$ system and the linear l-connected-(k, r)-out-of-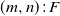$(m,n)\colon\! F$ system without/with overlapping. Reliabilities of these systems are studied via the finite Markov chain imbedding approach (FMCIA) in a novel way. Some numerical examples are provided to illustrate the theoretical results established here and also to demonstrate the efficiency of the developed method. Finally, some possible applications and generalizations of the developed results are pointed out.

Keywords

Reliabilitylinear two-dimensional consecutive k-type systemoverlappingnon-overlappingfinite Markov chain imbedding approach (FMCIA)

MSC classification

Primary: 90B25: Reliability, availability, maintenance, inspection
Secondary: 60G10: Stationary processes
Type
Original Article
Information
Journal of Applied Probability , Volume 61 , Issue 2 , June 2024 , pp. 439 - 464
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Akiba, T. and Yamamoto, H. (2001). Reliability of 2-dimensional k-within-consecutive- $r\times s$ -out-of- $m \times n\colon\! F$ lattice system. Naval Res. Logistics 48, 625–637.10.1002/nav.1038CrossRefGoogle Scholar
Amini-Seresht, E. and Balakrishnan, N. (2021). Stochastic properties of generalized finite mixture models with dependent components. J. Appl. Prob. 58, 794–804.10.1017/jpr.2021.4CrossRefGoogle Scholar
Balakrishnan, N. and Koutras, M. V. (2002). Runs and Scans with Applications. Wiley, New York.Google Scholar
Balakrishnan, N., Barmalzan, G. and Haidari, A. (2018). On stochastic comparisons of k-out-of-n systems with Weibull components. J. Appl. Prob. 55, 216–232.10.1017/jpr.2018.14CrossRefGoogle Scholar
Balakrishnan, N., Koutras, M. V. and Milienos, F. S. (2021). Reliability Analysis and Plans for Successive Testing: Start-up Demonstration Tests and Applications. Academic Press, San Diego.Google Scholar
Boehme, T. K., Kossow, A. and Preuss, W. (1992). A generalization of consecutive-k-out-of- $n\colon\! F$ systems. IEEE Trans. Reliab. 41, 451–457.10.1109/24.159819CrossRefGoogle Scholar
Chang, G. J., Cui, L. R. and Hwang, F. K. (2000). Reliabilities of Consecutive-k Systems. Kluwer Academic Publishers, Dordrecht.Google Scholar
Chang, Y. M. and Huang, T. H. (2010). Reliability of a 2-dimensional k-within-consecutive- $r\times s$ -out-of- $m\times n\colon\! F$ system using finite Markov chains. IEEE Trans. Reliab. 59, 725–733.10.1109/TR.2010.2085510CrossRefGoogle Scholar
Chen, J. and Glaz, J. (1996). Two-dimensional discrete scan statistics. Statist. Prob. Lett. 31, 59–68.10.1016/0167-7152(95)00014-3CrossRefGoogle Scholar
Cui, L. R., Xu, Y. and Zhao, X. (2010). Developments and applications of the finite Markov chain imbedding approach in reliability. IEEE Trans. Reliab. 59, 685–690.10.1109/TR.2010.2054172CrossRefGoogle Scholar
Ding, W. Y., Fang, R. and Zhao, P. (2019). Reliability analysis of k-out-of-n systems based on a grouping of components. Adv. Appl. Prob. 51, 339–357.10.1017/apr.2019.22CrossRefGoogle Scholar
Fu, J. C. and Koutras, M. V. (1994). Distribution theory of runs: a Markov chain approach. J. Amer. Statist. Assoc. 89, 1050–1058.10.1080/01621459.1994.10476841CrossRefGoogle Scholar
Fu, J. C. and Koutras, M. V. (1994). Poisson approximations for 2-dimensional patterns. Ann. Inst. Statist. Math. 46, 179–192.10.1007/BF00773602CrossRefGoogle Scholar
Fu, J. C. and Lou, W. W. (2003). Distribution Theory of Runs and Patterns and Its Applications: A Finite Markov Chain Imbedding Approach. World Scientific, Singapore.10.1142/4669CrossRefGoogle Scholar
Fu, J. C. and Wu, T. L. (2010). Boundary crossing probabilities for high-dimensional Brownian motion. J. Appl. Prob. 53, 543–553.10.1017/jpr.2016.19CrossRefGoogle Scholar
Fu, J. C. and Wu, T. L. (2010). Linear and nonlinear boundary crossing probabilities for Brownian motion and related processes. J. Appl. Prob. 47, 1058–1071.10.1239/jap/1294170519CrossRefGoogle Scholar
Godbole, A. P., Potter, L. K. and Sklar, J. K. (1998). Improved upper bounds for the reliability of d-dimensional consecutive-k-out-of- $n\colon\! F$ systems. Naval Res. Logistics 45, 219–230.10.1002/(SICI)1520-6750(199803)45:2<219::AID-NAV6>3.0.CO;2-B3.0.CO;2-B>CrossRefGoogle Scholar
Habib, A. S., Yuge, T., Al-Seedy, R. O. and Ammar, S. I. (2010). Reliability of a consecutive (r, s)-out-of- $(m,n)\colon\! F$ lattice system with conditions on the number of failed components in the system. Appl. Math. Model. 34, 531–538.10.1016/j.apm.2009.06.022CrossRefGoogle Scholar
Hsieh, Y. C. and Chen, T. C. (2004). Reliability lower bound for two-dimensional consecutive-k-out-of- $n\colon\! F$ systems. Comput. Operat. Res. 31, 1259–1272.10.1016/S0305-0548(03)00079-0CrossRefGoogle Scholar
Koutras, M. V. (1996). On a Markov chain approach for the study of reliability structures. J. Appl. Prob. 33, 357–367.10.2307/3215059CrossRefGoogle Scholar
Koutras, M. V., Papadopoulos, G. K. and Papastavridis, S. G. (1993). Reliability of 2-dimensional consecutive-k-out-of- $n\colon\! F$ systems. IEEE Trans. Reliab. 42, 488–490.10.1109/24.273602CrossRefGoogle Scholar
Lin, C., Zeng, Z. Y., Zhou, Y., Xu, M. and Ren, Z. Y. (2019). A lower bound of reliability calculating method for lattice system with non-homogeneous components. Reliab. Eng. Syst. Saf. 188, 36–46.10.1016/j.ress.2019.03.009CrossRefGoogle Scholar
Lin, D. M. and Zuo, M. J. (2000). Reliability evaluation of a linear k-within-(r, s)-out-of- $(m,n)\colon\! F$ lattice system. Prob. Eng. Inf. Sci. 14, 435–443.10.1017/S0269964800144031CrossRefGoogle Scholar
Malinowski, J. and Preuss, W. (1995). On the reliability of generalized consecutive systems-a survey. Internat. J. Reliab. Qual. Saf. Eng. 2, 187–201.10.1142/S0218539395000150CrossRefGoogle Scholar
Nakamura, T., Yamamoto, H. and Shinzato, T. (2017). Proposal of calculation method for reliability of toroidal connected-(1,2)-or-(2,1)-out-of- $(m,n)\colon\! F$ lattice system with Markov chain. In Reliability Modelling with Computer and Maintenance Applications, ed. S. Nakamura, C. H. Qian and T. Nakagawa, pp. 139–153. World Scientific, Singapore.Google Scholar
Nakamura, T., Yamamoto, H. and Xiao, X. (2018). Fast calculation methods for reliability of connected-(r, s)-out-of- $(m,n)\colon\! F$ lattice system in special cases. Internat. J. Math. Eng. Manag. Sci. 392, 113–122.Google Scholar
Papastavridis, S. (1987). A limit theorem for the reliability of a consecutive-k-out-of-n system. Adv. Appl. Prob. 19, 746–748.10.2307/1427417CrossRefGoogle Scholar
Salvia, A. A. and Lasher, W. C. (1990). 2-dimensional consecutive-k-out-of- $n\colon\! F$ models. IEEE Trans. Reliab. 39, 382–385.10.1109/24.103023CrossRefGoogle Scholar
Yamamoto, H. (1996). Reliability of a connected- $({r_1},{s_1})$ -or- $({r_2},{s_2})$ - $\cdots$ - $({r_k},{s_k})$ -out-of- $(m,n)\colon\! F$ lattice system. Microelectron. Reliab. 36, 151–168.CrossRefGoogle Scholar
Yamamoto, H. and Akiba, T. (2005). A recursive algorithm for the reliability of a circular connected-(r, s)-out-of- $(m,n)\colon\! F$ lattice system. Comput. Ind. Eng. 49, 21–34.10.1016/j.cie.2005.01.015CrossRefGoogle Scholar
Yamamoto, H. and Akiba, T. (2005). Evaluating methods for the reliability of a large 2-dimensional rectangular k-within-consecutive-(r, s)-out-of- $(m,n)\colon\! F$ system. Naval Res. Logistics 52, 243–252.Google Scholar
Yamamoto, H. and Miyakawa, M. (1995). Reliability of a linear connected-(r, s)-out-of- $(m,n)\colon\! F$ lattice system. IEEE Trans. Reliab. 44, 333–336.10.1109/24.387391CrossRefGoogle Scholar
Yamamoto, H. and Miyakawa, M. (1996). Reliability of circular connected-(r, s)-out-of-(m, n) lattice system. J. Operat. Res. Soc. Japan 39, 389–406.10.15807/jorsj.39.389CrossRefGoogle Scholar
Yi, H., Cui, L. R. and Gao, H. D. (2020). Reliabilities of some multistate consecutive-k systems. IEEE Trans. Reliab. 69, 414–429.10.1109/TR.2019.2897726CrossRefGoogle Scholar
Zhao, X, Cui, L. R., Zhao, W. and Liu, F. (2010). Exact reliability of a linear connected-(r, s)-out-of-(m, n) system. IEEE Trans. Reliab. 60, 689–698.10.1109/TR.2011.2139770CrossRefGoogle Scholar
Zhao, X., Zhao, W. and Xie, W. J. (2011). Two-dimensional linear connected-k system with trinary states and its reliability. J. Syst. Eng. Electron. 22, 866–870.10.3969/j.issn.1004-4132.2011.05.020CrossRefGoogle Scholar