Hostname: page-component-848d4c4894-ndmmz Total loading time: 0 Render date: 2024-06-02T02:09:19.365Z Has data issue: false hasContentIssue false
  • English
  • Français

Distributed lag regression by an almost periodic design matrix

Published online by Cambridge University Press:  14 July 2016

M. J. Katzoff  and
R. H. Shumway
M. J. Katzoff
Affiliation:
NHI Modeling Group, Social Security Administration
R. H. Shumway
Affiliation:
The George Washington University, Washington, D.C.
Get access Rights & Permissions [Opens in a new window]

Abstract

Frequency domain estimation and tests of hypotheses are considered for a general multivariate distributed lag regression model. The usual vector of regression functions is replaced by a matrix of almost periodic functions, a case for which the terms appearing in the frequency domain estimators have well-defined limits. Asymptotic distributions and consistency are established for the regression coefficients and error spectra. A test statistic is proposed for the no regression hypothesis which is asymptotically central 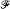under the null hypothesis and converges to infinity under the alternative. In the multivariate case, a product of beta-distributed variables is obtained.

Keywords

STATIONARY TIME SERIESFINITE FOURIER TRANSFORMTESTS OF HYPOTHESESASYMPTOTIC DISTRIBUTIONS
Type
Research Papers
Information
Journal of Applied Probability , Volume 15 , Issue 4 , December 1978 , pp. 759 - 773
Copyright
Copyright © Applied Probability Trust 1978 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Anderson, T. W. (1971) The Statistical Analysis of Time Series. Wiley, New York.Google Scholar
[2] Besicovitch, A. S. (1958) Almost Periodic Functions. Dover, New York.Google Scholar
[3] Billingsley, P. (1968) Convergence of Probability Measures. Wiley, New York.Google Scholar
[4] Brillinger, D. R. (1969) A search for a relationship between monthly sunspot numbers and certain climactic series. Bull. I.S.I., Proc. 37th Session , XLIII(1), 293–307.Google Scholar
[5] Corduneanu, C. (1968) Almost Periodic Functions. Wiley, New York.Google Scholar
[6] Goodman, N. R. (1963) Statistical analysis based on a certain multivariate complex Gaussian distribution (an introduction). Ann. Math. Statist. 34, 152–177.Google Scholar
[7] Grenander, U. and Rosenblatt, M. (1957) Statistical Analysis of Stationary Time Series. Wiley, New York.Google Scholar
[8] Hannan, E. J. (1970) Multiple Time Series. Wiley, New York.Google Scholar
[9] Holevo, A. S. (1971) Estimators of an almost periodic time signal. Theory Prob. Appl. 16, 249–263.Google Scholar
[10] Khatri, C. G. (1965) Classical statistical analysis based on a certain multivariate complex Gaussian distribution. Ann. Math. Statist. 36, 98–114.Google Scholar
[11] Kirkendall, N. (1974) Large Sample Finite Approximations in an Infinite Dimensional Distributed Lag Model. Ph.D. Dissertation, The George Washington University.Google Scholar
[12] Koopmans, H. L. (1974) The Spectral Analysis of Time Series. Academic Press, New York.Google Scholar
[13] Shumway, R. H. (1970) Applied regression and analysis of variance for stationary time series. J. Amer. Statist. Assoc. 65, 1527–1546.Google Scholar
[14] Wahba, G. (1969) Estimation of the coefficient in a multidimensional distributed lag model. Econometrica 37, 398–407.Google Scholar