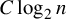1 Introduction
An induced subgraph of a graph is called homogeneous if it is a clique or independent set (i.e., all possible edges are present, or none are). One of the most fundamental results in Ramsey theory, proved in 1935 by Erdős and Szekeres [Reference Erdős and Szekeres38], states that every n-vertex graph contains a homogeneous subgraph with at least
![]() $\frac {1}{2}\log _{2}n$
vertices.Footnote 1 On the other hand, Erdős [Reference Erdős33] famously used the probabilistic method to prove that, for all
$\frac {1}{2}\log _{2}n$
vertices.Footnote 1 On the other hand, Erdős [Reference Erdős33] famously used the probabilistic method to prove that, for all
![]() $n\ge 3$
, there is an n-vertex graph with no homogeneous subgraph on
$n\ge 3$
, there is an n-vertex graph with no homogeneous subgraph on
![]() $2\log _{2}n$
vertices. Despite significant effort (see, for example, [Reference Barak, Rao, Shaltiel and Wigderson11, Reference Li71, Reference Chattopadhyay and Zuckerman20, Reference Frankl and Wilson47, Reference Cohen24, Reference Chung21, Reference Nagy75, Reference Abbott1, Reference Frankl48, Reference Gopalan52]), there are no known nonprobabilistic constructions of graphs with comparably small homogeneous sets, and in fact the problem of explicitly constructing such graphs is intimately related to randomness extraction in theoretical computer science (see, for example, [Reference Shaltiel89] for an introduction to the topic).
$2\log _{2}n$
vertices. Despite significant effort (see, for example, [Reference Barak, Rao, Shaltiel and Wigderson11, Reference Li71, Reference Chattopadhyay and Zuckerman20, Reference Frankl and Wilson47, Reference Cohen24, Reference Chung21, Reference Nagy75, Reference Abbott1, Reference Frankl48, Reference Gopalan52]), there are no known nonprobabilistic constructions of graphs with comparably small homogeneous sets, and in fact the problem of explicitly constructing such graphs is intimately related to randomness extraction in theoretical computer science (see, for example, [Reference Shaltiel89] for an introduction to the topic).
For some
![]() $C>0$
, an n-vertex graph is called C-Ramsey if it has no homogeneous subgraph of size
$C>0$
, an n-vertex graph is called C-Ramsey if it has no homogeneous subgraph of size
![]() $C\log _{2}n$
. We think of C as being a constant (not varying with n), so C-Ramsey graphs are those graphs with near-optimal Ramsey behavior. It is widely believed that C-Ramsey graphs must in some sense resemble random graphs (which would provide some explanation for why it is so hard to find explicit constructions), and this belief has been supported by a number of theorems showing that certain structural or statistical properties characteristic of random graphs hold for all C-Ramsey graphs. The first result of this type was due to Erdős and Szemerédi [Reference Erdős and Szemerédi39], who showed that every C-Ramsey graph G has edge-density bounded away from zero and one (formally, for any
$C\log _{2}n$
. We think of C as being a constant (not varying with n), so C-Ramsey graphs are those graphs with near-optimal Ramsey behavior. It is widely believed that C-Ramsey graphs must in some sense resemble random graphs (which would provide some explanation for why it is so hard to find explicit constructions), and this belief has been supported by a number of theorems showing that certain structural or statistical properties characteristic of random graphs hold for all C-Ramsey graphs. The first result of this type was due to Erdős and Szemerédi [Reference Erdős and Szemerédi39], who showed that every C-Ramsey graph G has edge-density bounded away from zero and one (formally, for any
![]() $C>0$
there is
$C>0$
there is
![]() $\varepsilon _{C}>0$
such that for sufficiently large n, the number of edges in any C-Ramsey graph with n vertices lies between
$\varepsilon _{C}>0$
such that for sufficiently large n, the number of edges in any C-Ramsey graph with n vertices lies between
![]() $\varepsilon _{C}\binom {n}{2}$
and
$\varepsilon _{C}\binom {n}{2}$
and
![]() $(1-\varepsilon _{C})\binom {n}{2}$
). Note that this implies fairly strong information about the edge distribution on induced subgraphs of G because any induced subgraph of G with at least
$(1-\varepsilon _{C})\binom {n}{2}$
). Note that this implies fairly strong information about the edge distribution on induced subgraphs of G because any induced subgraph of G with at least
![]() $n^{\alpha }$
vertices is itself
$n^{\alpha }$
vertices is itself
![]() $(C/\alpha )$
-Ramsey.
$(C/\alpha )$
-Ramsey.
This basic result was the foundation for a large amount of further research on Ramsey graphs; over the years, many conjectures have been proposed and many theorems proved (see, for example, [Reference Alon and Hajnal2, Reference Alon, Balogh, Kostochka and Samotij3, Reference Alon and Bollobás4, Reference Alon and Kostochka7, Reference Alon, Krivelevich and Sudakov8, Reference Bukh and Sudakov16, Reference Erdős and Hajnal37, Reference Erdős34, Reference Jenssen, Keevash, Long and Yepremyan60, Reference Kwan and Sudakov66, Reference Kwan and Sudakov67, Reference Narayanan, Sahasrabudhe and Tomon76, Reference Prömel and Rödl84, Reference Shelah90, Reference Alon and Orlitsky9, Reference Lauria, Pudlák, Rödl and Thapen70]). Particular attention has focused on a sequence of conjectures made by Erdős and his collaborators, exploring the theme that Ramsey graphs must have diverse induced subgraphs. For example, for a C-Ramsey graph G with n vertices, it was proved by Prömel and Rödl [Reference Prömel and Rödl84] (answering a conjecture of Erdős and Hajnal) that G contains every possible induced subgraph on
![]() $\delta _{C}\log n$
vertices; by Shelah [Reference Shelah90] (answering a conjecture of Erdős and Rényi) that G contains
$\delta _{C}\log n$
vertices; by Shelah [Reference Shelah90] (answering a conjecture of Erdős and Rényi) that G contains
![]() $2^{\delta _{C}n}$
nonisomorphic induced subgraphs; by the first author and Sudakov [Reference Kwan and Sudakov66] (answering a conjecture of Erdős, Faudree and Sós) that G contains
$2^{\delta _{C}n}$
nonisomorphic induced subgraphs; by the first author and Sudakov [Reference Kwan and Sudakov66] (answering a conjecture of Erdős, Faudree and Sós) that G contains
![]() $\delta _{C}n^{5/2}$
subgraphs that can be distinguished by looking at their edge and vertex numbers and by Jenssen, Keevash, Long and Yepremyan [Reference Jenssen, Keevash, Long and Yepremyan60] (improving on a conjecture of Erdős, Faudree and Sós proved by Bukh and Sudakov [Reference Bukh and Sudakov16]) that G contains an induced subgraph with
$\delta _{C}n^{5/2}$
subgraphs that can be distinguished by looking at their edge and vertex numbers and by Jenssen, Keevash, Long and Yepremyan [Reference Jenssen, Keevash, Long and Yepremyan60] (improving on a conjecture of Erdős, Faudree and Sós proved by Bukh and Sudakov [Reference Bukh and Sudakov16]) that G contains an induced subgraph with
![]() $\delta _C n^{2/3}$
distinct degrees (all for some
$\delta _C n^{2/3}$
distinct degrees (all for some
![]() $\delta _{C}>0$
depending on C).
$\delta _{C}>0$
depending on C).
Only one of Erdős’ conjectures (on properties of C-Ramsey graphs) from this period has remained open until now: Erdős and McKay (see [Reference Erdős34]) made the ambitious conjecture that for essentially any ‘sensible’ integer x, every C-Ramsey graph must necessarily contain an induced subgraph with exactly x edges. To be precise, they conjectured that there is
![]() $\delta _{C}>0$
depending on C such that for any C-Ramsey graph G with n vertices and any integer
$\delta _{C}>0$
depending on C such that for any C-Ramsey graph G with n vertices and any integer
![]() $0\le x\le \delta _{C}n^{2}$
, there is an induced subgraph of G with exactly x edges. Erdős reiterated this problem in several collections of his favorite open problems in combinatorics [Reference Erdős34, Reference Erdős35] (also in [Reference Erdős36]) and offered one of his notorious monetary prizes ($100) for its solution (see [Reference Erdős35, Reference Chung and Graham23, Reference Chung22]).
$0\le x\le \delta _{C}n^{2}$
, there is an induced subgraph of G with exactly x edges. Erdős reiterated this problem in several collections of his favorite open problems in combinatorics [Reference Erdős34, Reference Erdős35] (also in [Reference Erdős36]) and offered one of his notorious monetary prizes ($100) for its solution (see [Reference Erdős35, Reference Chung and Graham23, Reference Chung22]).
Progress on the Erdős–McKay conjecture has come from four different directions. First, the canonical example of a Ramsey graph is (a typical outcome of) an Erdős–Rényi random graph. It was proved by Calkin, Frieze and McKay [Reference Calkin, Frieze and McKay17] (answering questions raised by Erdős and McKay) that for any constants
![]() $p\in (0,1)$
and
$p\in (0,1)$
and
![]() $\eta>0$
, a random graph
$\eta>0$
, a random graph
![]() $\mathbb {G}(n,p)$
typically contains induced subgraphs with all numbers of edges up to
$\mathbb {G}(n,p)$
typically contains induced subgraphs with all numbers of edges up to
![]() $(1-\eta )p\binom {n}{2}$
. Second, improving on initial bounds of Erdős and McKay [Reference Erdős34], it was proved by Alon, Krivelevich and Sudakov [Reference Alon, Krivelevich and Sudakov8] that there is
$(1-\eta )p\binom {n}{2}$
. Second, improving on initial bounds of Erdős and McKay [Reference Erdős34], it was proved by Alon, Krivelevich and Sudakov [Reference Alon, Krivelevich and Sudakov8] that there is
![]() $\alpha _{C}>0$
such that in a C-Ramsey graph on n vertices, one can always find an induced subgraph with any given number of edges up to
$\alpha _{C}>0$
such that in a C-Ramsey graph on n vertices, one can always find an induced subgraph with any given number of edges up to
![]() $n^{\alpha _{C}}$
. Third, improving on a result of Narayanan, Sahasrabudhe and Tomon [Reference Narayanan, Sahasrabudhe and Tomon76], the first author and Sudakov [Reference Kwan and Sudakov67] proved that there is
$n^{\alpha _{C}}$
. Third, improving on a result of Narayanan, Sahasrabudhe and Tomon [Reference Narayanan, Sahasrabudhe and Tomon76], the first author and Sudakov [Reference Kwan and Sudakov67] proved that there is
![]() $\delta _{C}>0$
such that in any C-Ramsey graph on n vertices contains induced subgraphs with
$\delta _{C}>0$
such that in any C-Ramsey graph on n vertices contains induced subgraphs with
![]() $\delta _{C}n^{2}$
different numbers of edges (though without making any guarantee on what those numbers of edges are). Finally, Long and Ploscaru [Reference Long and Ploscaru72] recently proved a bipartite analog of the Erdős–McKay conjecture.
$\delta _{C}n^{2}$
different numbers of edges (though without making any guarantee on what those numbers of edges are). Finally, Long and Ploscaru [Reference Long and Ploscaru72] recently proved a bipartite analog of the Erdős–McKay conjecture.
As our first result, we prove a substantial strengthening of the Erdős–McKay conjecture.Footnote 2 Let
![]() $e(G)$
be the number of edges in a graph G.
$e(G)$
be the number of edges in a graph G.
Theorem 1.1. Fix
![]() $C> 0$
and
$C> 0$
and
![]() $\eta>0$
, and let G be a C-Ramsey graph on n vertices, where n is sufficiently large with respect to C and
$\eta>0$
, and let G be a C-Ramsey graph on n vertices, where n is sufficiently large with respect to C and
![]() $\eta $
. Then for any integer x with
$\eta $
. Then for any integer x with
![]() $0\leq x\leq (1-\eta )e(G)$
, there is a subset
$0\leq x\leq (1-\eta )e(G)$
, there is a subset
![]() $U\subseteq V(G)$
inducing exactly x edges.
$U\subseteq V(G)$
inducing exactly x edges.
Given prior results due to Alon, Krivelevich and Sudakov [Reference Alon, Krivelevich and Sudakov8], Theorem 1.1 is actually a simple corollary of a much deeper result (Theorem 1.2) on edge statistics in Ramsey graphs, which we discuss in the next subsection.
1.1 Edge statistics and low-degree polynomials
For an n-vertex graph G, observe that the number of edges
![]() $e(G[U])$
in an induced subgraph
$e(G[U])$
in an induced subgraph
![]() $G[U]$
can be viewed as an evaluation of a quadratic polynomial associated with G. Indeed, identifying the vertex set of G with
$G[U]$
can be viewed as an evaluation of a quadratic polynomial associated with G. Indeed, identifying the vertex set of G with
![]() $\{1,\ldots ,n\}$
and writing E for the edge set of G, consider the n-variable quadratic polynomial
$\{1,\ldots ,n\}$
and writing E for the edge set of G, consider the n-variable quadratic polynomial
![]() $f(\xi _{1},\ldots ,\xi _{n})=\sum _{ij\in E}\xi _{i}\xi _{j}$
. Then, for any vertex set U, let
$f(\xi _{1},\ldots ,\xi _{n})=\sum _{ij\in E}\xi _{i}\xi _{j}$
. Then, for any vertex set U, let
![]() $\vec {\xi }\,^{(U)}$
be the characteristic vector of U (with
$\vec {\xi }\,^{(U)}$
be the characteristic vector of U (with
![]() $\vec {\xi }\,^{(U)}_v=1$
if
$\vec {\xi }\,^{(U)}_v=1$
if
![]() $v\in U$
, and
$v\in U$
, and
![]() $\vec {\xi }\,^{(U)}_v=0$
if
$\vec {\xi }\,^{(U)}_v=0$
if
![]() $v\notin U$
). It is easy to check that the number of edges
$v\notin U$
). It is easy to check that the number of edges
![]() $e(G[U])$
induced by U is precisely equal to
$e(G[U])$
induced by U is precisely equal to
![]() $f(\vec {\xi }\,^{(U)})$
. That is, to say, the statement that G has an induced subgraph with exactly x edges is precisely equivalent to the statement that there is a binary vector
$f(\vec {\xi }\,^{(U)})$
. That is, to say, the statement that G has an induced subgraph with exactly x edges is precisely equivalent to the statement that there is a binary vector
![]() $\vec {\xi }\in \{0,1\}^n$
with
$\vec {\xi }\in \{0,1\}^n$
with
![]() $f(\vec {\xi })=x$
.
$f(\vec {\xi })=x$
.
There are many combinatorial quantities of interest that can be interpreted as low-degree polynomials of binary vectors. For example, the number of triangles in a graph, or the number of three-term arithmetic progressions in a set of integers, can both be naturally interpreted as evaluations of certain cubic polynomials. More generally, the study of Boolean functions is the study of functions of the form
![]() $f\colon \{0,1\}^{n}\to \mathbb {R}$
; every such function can be written (uniquely) as a multilinear polynomial, and the degree of this polynomial is a fundamental measure of the ‘complexity’ of the Boolean function.
$f\colon \{0,1\}^{n}\to \mathbb {R}$
; every such function can be written (uniquely) as a multilinear polynomial, and the degree of this polynomial is a fundamental measure of the ‘complexity’ of the Boolean function.
One of the most important discoveries from the analysis of Boolean functions is that it is fruitful to study the behavior of (low-degree) Boolean functions evaluated on a random binary vector
![]() $\vec {\xi }\in \{0,1\}^n$
. This is the perspective we take in this paper: As our main result, for any Ramsey graph G and a random vertex subset U, we obtain very precise control over the distribution of
$\vec {\xi }\in \{0,1\}^n$
. This is the perspective we take in this paper: As our main result, for any Ramsey graph G and a random vertex subset U, we obtain very precise control over the distribution of
![]() $e(G[U])$
.
$e(G[U])$
.
Theorem 1.2. Fix
![]() $C,\lambda> 0$
, let G be a C-Ramsey graph on n vertices and let
$C,\lambda> 0$
, let G be a C-Ramsey graph on n vertices and let
![]() $\lambda \le p\le 1-\lambda $
. Then if U is a random subset of
$\lambda \le p\le 1-\lambda $
. Then if U is a random subset of
![]() $V(G)$
obtained by independently including each vertex with probability p, we have
$V(G)$
obtained by independently including each vertex with probability p, we have
for some
![]() $K_{C,\lambda }>0$
depending only on
$K_{C,\lambda }>0$
depending only on
![]() $C,\lambda $
. Furthermore, for every fixed
$C,\lambda $
. Furthermore, for every fixed
![]() $A>0$
, we have
$A>0$
, we have
 $$\begin{align*}\qquad\inf_{\substack{x\in\mathbb{Z}\\|x-p^2e(G)|\le An^{3/2}}}\Pr[e(G[U])=x] \ge \kappa_{C,A,\lambda}n^{-3/2}\end{align*}$$
$$\begin{align*}\qquad\inf_{\substack{x\in\mathbb{Z}\\|x-p^2e(G)|\le An^{3/2}}}\Pr[e(G[U])=x] \ge \kappa_{C,A,\lambda}n^{-3/2}\end{align*}$$
for some
![]() $\kappa _{C,A,\lambda }>0$
depending only on
$\kappa _{C,A,\lambda }>0$
depending only on
![]() $C,A,\lambda $
, if n is sufficiently large in terms of
$C,A,\lambda $
, if n is sufficiently large in terms of
![]() $C,\lambda $
and A.
$C,\lambda $
and A.
It is not hard to show that for any C-Ramsey graph G, the standard deviation
![]() $\sigma $
of
$\sigma $
of
![]() $e(G[U])$
is of order
$e(G[U])$
is of order
![]() $n^{3/2}$
. So, Theorem 1.2 says (roughly speaking) that in the ‘bulk’ of the distribution of
$n^{3/2}$
. So, Theorem 1.2 says (roughly speaking) that in the ‘bulk’ of the distribution of
![]() $e(G[U])$
(i.e., within roughly standard-deviation range of the mean), the point probabilities are all of order
$e(G[U])$
(i.e., within roughly standard-deviation range of the mean), the point probabilities are all of order
![]() $1/\sigma $
. In Section 2, we will give the short deduction of Theorem 1.1 from Theorem 1.2 and the aforementioned theorem of Alon, Krivelevich and Sudakov.
$1/\sigma $
. In Section 2, we will give the short deduction of Theorem 1.1 from Theorem 1.2 and the aforementioned theorem of Alon, Krivelevich and Sudakov.
Remark 1.3. Our proof of Theorem 1.2 can be adapted to handle slightly more general types of graphs than Ramsey graphs. For example, we can obtain the same conclusions in the case where G is a d-regular graph with
![]() $0.01n\le d\le 0.99n$
, such that the eigenvalues
$0.01n\le d\le 0.99n$
, such that the eigenvalues
![]() $\lambda _1\ge \cdots \ge \lambda _n$
of the adjacency matrix of G satisfy
$\lambda _1\ge \cdots \ge \lambda _n$
of the adjacency matrix of G satisfy
![]() $\max \{\lambda _2,-\lambda _n\}\le n^{1/2+0.01}$
(i.e., the case where G is a dense graph with near-optimal spectral expansion). See Remarks 4.5 and 4.2 for some discussion of the necessary adaptations. Notably, this class of graphs includes Paley graphs, which are ‘random-like’ graphs with an explicit number-theoretic definition (see, for example, [Reference Krivelevich and Sudakov63]). These graphs are currently one of the most promising candidates for explicit constructions of Ramsey graphs, though precisely studying the Ramsey properties of these graphs seems to be outside the reach of current techniques in number theory (see [Reference Hanson and Petridis56, Reference Di Benedetto, Solymosi and White29] for recent developments).
$\max \{\lambda _2,-\lambda _n\}\le n^{1/2+0.01}$
(i.e., the case where G is a dense graph with near-optimal spectral expansion). See Remarks 4.5 and 4.2 for some discussion of the necessary adaptations. Notably, this class of graphs includes Paley graphs, which are ‘random-like’ graphs with an explicit number-theoretic definition (see, for example, [Reference Krivelevich and Sudakov63]). These graphs are currently one of the most promising candidates for explicit constructions of Ramsey graphs, though precisely studying the Ramsey properties of these graphs seems to be outside the reach of current techniques in number theory (see [Reference Hanson and Petridis56, Reference Di Benedetto, Solymosi and White29] for recent developments).
Remark 1.4. If
![]() $p=1/2$
, then the random set U in Theorem 1.2 is simply a uniformly random subset of vertices. So, for x close to
$p=1/2$
, then the random set U in Theorem 1.2 is simply a uniformly random subset of vertices. So, for x close to
![]() $e(G)/4$
, Theorem 1.2 tells us that the number of induced subgraphs with x edges is of order
$e(G)/4$
, Theorem 1.2 tells us that the number of induced subgraphs with x edges is of order
![]() $2^n/n^{3/2}$
. It would be interesting to investigate the number of x-edge induced subgraphs for general x (not close to
$2^n/n^{3/2}$
. It would be interesting to investigate the number of x-edge induced subgraphs for general x (not close to
![]() $e(G)/4$
). From Theorem 1.2, one can deduce a lower bound on this number approximately matching the behavior of an appropriate Erdős–Rényi random graph (i.e., for any constant
$e(G)/4$
). From Theorem 1.2, one can deduce a lower bound on this number approximately matching the behavior of an appropriate Erdős–Rényi random graph (i.e., for any constant
![]() $\eta>0$
, and
$\eta>0$
, and
![]() $\eta n^2\le x\le (1-\eta )e(G)$
, there are at least
$\eta n^2\le x\le (1-\eta )e(G)$
, there are at least
![]() $\exp (H(\sqrt {x/e(G)})n + o(n))$
subgraphs with x edges, where H denotes the base-e entropy function). However, a corresponding upper bound does not in general hold: To characterize the number of x-edge induced subgraphs up to any subexponential error term, one must incorporate more detailed information about the Ramsey graph G than just its number of edges. (To see this, consider a union of two disjoint independent Erdős–Rényi random graphs
$\exp (H(\sqrt {x/e(G)})n + o(n))$
subgraphs with x edges, where H denotes the base-e entropy function). However, a corresponding upper bound does not in general hold: To characterize the number of x-edge induced subgraphs up to any subexponential error term, one must incorporate more detailed information about the Ramsey graph G than just its number of edges. (To see this, consider a union of two disjoint independent Erdős–Rényi random graphs
![]() $\mathbb G(n/2,0.01)\sqcup \mathbb G(n/2,0.99)$
, and count subgraphs with
$\mathbb G(n/2,0.01)\sqcup \mathbb G(n/2,0.99)$
, and count subgraphs with
![]() $0.001n^2$
edges.)
$0.001n^2$
edges.)
There has actually been quite some recent interest (see, for example, [Reference Kwan, Sudakov and Tran68, Reference Fox, Kwan and Sauermann44, Reference Martinsson, Mousset, Noever and Trujić73, Reference Fox and Sauermann45, Reference Alon, Hefetz, Krivelevich and Tyomkyn6]) studying random variables of the form
![]() $e(G[U])$
for a graph G and a random vertex set U, largely due to a sequence of conjectures by Alon, Hefetz, Krivelevich and Tyomkyn [Reference Alon, Hefetz, Krivelevich and Tyomkyn6] motivated by the classical topic of graph inducibility. Specifically, these works studied the anticoncentration behavior of
$e(G[U])$
for a graph G and a random vertex set U, largely due to a sequence of conjectures by Alon, Hefetz, Krivelevich and Tyomkyn [Reference Alon, Hefetz, Krivelevich and Tyomkyn6] motivated by the classical topic of graph inducibility. Specifically, these works studied the anticoncentration behavior of
![]() $e(G[U])$
(generally speaking, anticoncentration inequalities provide upper bounds on the probability that a random variable falls in some small ball or is equal to some particular value). As discussed above,
$e(G[U])$
(generally speaking, anticoncentration inequalities provide upper bounds on the probability that a random variable falls in some small ball or is equal to some particular value). As discussed above,
![]() $e(G[U])$
can be naturally interpreted as a quadratic polynomial, so this study falls within the scope of the so-called polynomial Littlewood–Offord problem (which concerns anticoncentration of general low-degree polynomials of various types of random variables). There has been a lot of work from several different directions (see, for example, [Reference Costello26, Reference Kane61, Reference Kwan and Sauermann65, Reference Tao and Vu92, Reference Nguyen and Vu78, Reference Halász55, Reference Tao and Vu91, Reference Rudelson and Vershynin87, Reference Nguyen77, Reference Nguyen and Vu79]) on the extent to which anticoncentration in the (polynomial) Littlewood–Offord problem is controlled by algebraic or arithmetic structure, and the upper bound in Theorem 1.2 can be viewed in this context: Ramsey graphs yield quadratic polynomials that are highly unstructured in a certain combinatorial sense, and we see that such polynomials have strong anticoncentration behavior.
$e(G[U])$
can be naturally interpreted as a quadratic polynomial, so this study falls within the scope of the so-called polynomial Littlewood–Offord problem (which concerns anticoncentration of general low-degree polynomials of various types of random variables). There has been a lot of work from several different directions (see, for example, [Reference Costello26, Reference Kane61, Reference Kwan and Sauermann65, Reference Tao and Vu92, Reference Nguyen and Vu78, Reference Halász55, Reference Tao and Vu91, Reference Rudelson and Vershynin87, Reference Nguyen77, Reference Nguyen and Vu79]) on the extent to which anticoncentration in the (polynomial) Littlewood–Offord problem is controlled by algebraic or arithmetic structure, and the upper bound in Theorem 1.2 can be viewed in this context: Ramsey graphs yield quadratic polynomials that are highly unstructured in a certain combinatorial sense, and we see that such polynomials have strong anticoncentration behavior.
The first author, Sudakov and Tran [Reference Kwan, Sudakov and Tran68] previously suggested to study anticoncentration of
![]() $e(G[W])$
for a Ramsey graph G and a random vertex subset W of a given size. In particular, they asked whether for a C-Ramsey graph G with n vertices, and a uniformly random subset W of exactly
$e(G[W])$
for a Ramsey graph G and a random vertex subset W of a given size. In particular, they asked whether for a C-Ramsey graph G with n vertices, and a uniformly random subset W of exactly
![]() $n/2$
vertices, we have
$n/2$
vertices, we have
![]() $\sup _{x\in \mathbb {Z}}\Pr [e(G[W])=x]\le K_{C}/n$
for some
$\sup _{x\in \mathbb {Z}}\Pr [e(G[W])=x]\le K_{C}/n$
for some
![]() $K_{C}>0$
depending only on C. Some progress was made on this question by the first and third authors [Reference Kwan and Sauermann65]; as a simple corollary of Theorem 1.2, we answer this question in the affirmative.
$K_{C}>0$
depending only on C. Some progress was made on this question by the first and third authors [Reference Kwan and Sauermann65]; as a simple corollary of Theorem 1.2, we answer this question in the affirmative.
Theorem 1.5. For
![]() $C>0$
and
$C>0$
and
![]() $0<\lambda <1$
, there is
$0<\lambda <1$
, there is
![]() $K=K(C,\lambda )$
such that the following holds. Let G be a C-Ramsey graph on n vertices, and let
$K=K(C,\lambda )$
such that the following holds. Let G be a C-Ramsey graph on n vertices, and let
![]() $W\subseteq V(G)$
be a random subset of exactly k vertices, for some given k with
$W\subseteq V(G)$
be a random subset of exactly k vertices, for some given k with
![]() $\lambda n\le k\le (1-\lambda )n$
. Then
$\lambda n\le k\le (1-\lambda )n$
. Then
It is not hard to show that the upper bound in Theorem 1.5 is the best-possible (indeed, this can be seen by taking G to be a typical outcome of an Erdős–Rényi random graph
![]() $\mathbb G(n,1/2)$
). However, in contrast to the setting of Theorem 1.2, in Theorem 1.5 one cannot hope for a matching lower bound when x is close to
$\mathbb G(n,1/2)$
). However, in contrast to the setting of Theorem 1.2, in Theorem 1.5 one cannot hope for a matching lower bound when x is close to
![]() $\mathbb {E}[e(G[W])]$
(as can be seen by considering the case where G is a typical outcome of the union of two disjoint independent Erdős–Rényi random graphs
$\mathbb {E}[e(G[W])]$
(as can be seen by considering the case where G is a typical outcome of the union of two disjoint independent Erdős–Rényi random graphs
![]() $\mathbb G(n,1/4)\sqcup \mathbb G(n,3/4)$
).
$\mathbb G(n,1/4)\sqcup \mathbb G(n,3/4)$
).
1.2 Proof ingredients and ideas
We outline the proof of Theorem 1.2 in more detail in Section 3, but here we take the opportunity to highlight some of the most important ingredients and ideas.
1.2.1 An approximate local limit theorem
A starting point is that, in the setting of Theorem 1.2, standard techniques show that
![]() $e(G[U])$
satisfies a central limit theorem: We have
$e(G[U])$
satisfies a central limit theorem: We have
![]() $\Pr [e(G[U])\le x]=\Phi ((x-\mu )/\sigma )+o(1/\sigma )$
for all
$\Pr [e(G[U])\le x]=\Phi ((x-\mu )/\sigma )+o(1/\sigma )$
for all
![]() $x\in \mathbb {R}$
, where
$x\in \mathbb {R}$
, where
![]() $\Phi $
is the standard Gaussian cumulative distribution function, and
$\Phi $
is the standard Gaussian cumulative distribution function, and
![]() $\mu ,\sigma $
are the mean and standard deviation of
$\mu ,\sigma $
are the mean and standard deviation of
![]() $e(G[U])$
. It is natural to wonder (as suggested in [Reference Kwan and Sauermann65] as a potential path towards the Erdős–McKay conjecture) whether this can be strengthened to a local central limit theorem: Could it be that for all
$e(G[U])$
. It is natural to wonder (as suggested in [Reference Kwan and Sauermann65] as a potential path towards the Erdős–McKay conjecture) whether this can be strengthened to a local central limit theorem: Could it be that for all
![]() $x\in \mathbb R$
we have
$x\in \mathbb R$
we have
![]() $\Pr [e(G[U])=x]=\Phi '((x-\mu )/\sigma )/\sigma +o(1/\sigma )$
(where
$\Pr [e(G[U])=x]=\Phi '((x-\mu )/\sigma )/\sigma +o(1/\sigma )$
(where
![]() $\Phi '$
is the standard Gaussian density function)? In fact, the statement of Theorem 1.2 can be interpreted as a local central limit theorem ‘up to constant factors’. This perspective also suggests a strategy for the proof of Theorem 1.2: Perhaps we can leverage Fourier-analytic techniques previously developed for local central limit theorems (e.g., [Reference Gnedenko51, Reference Varjú94, Reference Berkowitz13, Reference Berkowitz12, Reference Gilmer and Kopparty50, Reference Kuperberg, Lovett and Peled64]), obtaining our desired result as a consequence of estimates on the characteristic function (i.e., Fourier transform) of our random variable
$\Phi '$
is the standard Gaussian density function)? In fact, the statement of Theorem 1.2 can be interpreted as a local central limit theorem ‘up to constant factors’. This perspective also suggests a strategy for the proof of Theorem 1.2: Perhaps we can leverage Fourier-analytic techniques previously developed for local central limit theorems (e.g., [Reference Gnedenko51, Reference Varjú94, Reference Berkowitz13, Reference Berkowitz12, Reference Gilmer and Kopparty50, Reference Kuperberg, Lovett and Peled64]), obtaining our desired result as a consequence of estimates on the characteristic function (i.e., Fourier transform) of our random variable
![]() $e(G[U])$
.
$e(G[U])$
.
However, it turns out that a local central limit theorem actually does not hold in general: While the coarse-scale distribution of
![]() $e(G[U])$
is always Gaussian, in general
$e(G[U])$
is always Gaussian, in general
![]() $e(G[U])$
may have a rather nontrivial ‘two-scale’ behavior, depending on the additive structure of the degree sequence of G (see Figure 1). Roughly speaking, this translates to a certain ‘spike’ in the magnitude of the characteristic function of
$e(G[U])$
may have a rather nontrivial ‘two-scale’ behavior, depending on the additive structure of the degree sequence of G (see Figure 1). Roughly speaking, this translates to a certain ‘spike’ in the magnitude of the characteristic function of
![]() $e(G[U])$
, which rules out naïve Fourier-analytic approaches. To overcome this issue, we need to capture the ‘reason’ for the two-scale behavior: It turns out that this ‘spike’ can only happen if the degree sequence of G is in a certain sense ‘additively structured’, implying that there is a partition of the vertex set into ‘buckets’ such that vertices in the same bucket have almost the same degree. Then, if we reveal the size of the intersection of U with each bucket, the conditional characteristic function of
$e(G[U])$
, which rules out naïve Fourier-analytic approaches. To overcome this issue, we need to capture the ‘reason’ for the two-scale behavior: It turns out that this ‘spike’ can only happen if the degree sequence of G is in a certain sense ‘additively structured’, implying that there is a partition of the vertex set into ‘buckets’ such that vertices in the same bucket have almost the same degree. Then, if we reveal the size of the intersection of U with each bucket, the conditional characteristic function of
![]() $e(G[U])$
is suitably bounded. We deduce conditional bounds on the point probabilities of
$e(G[U])$
is suitably bounded. We deduce conditional bounds on the point probabilities of
![]() $e(G[U])$
, and average these over possible outcomes of the revealed intersection sizes of U with the buckets.
$e(G[U])$
, and average these over possible outcomes of the revealed intersection sizes of U with the buckets.

Figure 1 On the left is a cartoon of (one possibility for) the probability mass function of
![]() $e(G[U])$
for a Ramsey graph G and a uniformly random vertex subset U: The large-scale behavior is Gaussian, but on a small scale we see many smaller Gaussian-like curves. The two images on the right are two different histograms at different scales, obtained from real data (namely, from two million independent samples of a uniformly random vertex subset in a graph G obtained as an outcome of the Erdős–Rényi random graph
$e(G[U])$
for a Ramsey graph G and a uniformly random vertex subset U: The large-scale behavior is Gaussian, but on a small scale we see many smaller Gaussian-like curves. The two images on the right are two different histograms at different scales, obtained from real data (namely, from two million independent samples of a uniformly random vertex subset in a graph G obtained as an outcome of the Erdős–Rényi random graph
![]() ${\mathbb G}(1000,0.8)$
).
${\mathbb G}(1000,0.8)$
).
We remark that one interpretation of our proof strategy is that we are decomposing our random variable into ‘components’ in physical space, in such a way that each component is well behaved in Fourier space. This is at least superficially reminiscent of certain techniques in harmonic analysis; see, for example, [Reference Guth54]. Looking beyond the particular statement of Theorem 1.2, we hope that the Fourier-analytic techniques in its proof will be useful for the general study of small-ball probability for low-degree polynomials of independent variables, especially in settings where Gaussian behavior may break down.
1.2.2 Small-ball probability for quadratic Gaussian chaos
The general study of low-degree polynomials of independent random variables (sometimes called chaoses) has a long and rich history. Some highlights include Kim–Vu polynomial concentration [Reference Kim and Vu62], the Hanson–Wright inequality [Reference Hanson and Wright57], the Bonami–Beckner hypercontractive inequality (see [Reference O’Donnell81]), and polynomial chaos expansion (see [Reference Ghanem and Spanos49]), which are fundamental tools in probabilistic combinatorics, high-dimensional statistics, the analysis of Boolean functions and mathematical modelling.
Much of this study has focused on low-degree polynomials of Gaussian random variables, which enjoy certain symmetry properties that make them easier to study. While this direction may not seem obviously relevant to Theorem 1.2, in part of the proof we are able to apply the celebrated Gaussian invariance principle of Mossel, O’Donnell and Oleszkiewicz [Reference Mossel, O’Donnell and Oleszkiewicz74], to compare our random variables of interest with certain ‘Gaussian analogs’. Therefore, a key step in the proof of Theorem 1.2 is to study small-ball probability for quadratic polynomials of Gaussian random variables.
The fundamental theorem in this area is the Carbery–Wright theorem [Reference Carbery and Wright19], which (specialized to the quadratic case) says that for
![]() $0<\varepsilon <1$
and any real quadratic polynomial
$0<\varepsilon <1$
and any real quadratic polynomial
![]() $f=f(Z_{1},\ldots ,Z_{n})$
of independent standard Gaussian random variables
$f=f(Z_{1},\ldots ,Z_{n})$
of independent standard Gaussian random variables
![]() $Z_{1},\ldots ,Z_{n}\sim \mathcal {N}(0,1)$
, we have
$Z_{1},\ldots ,Z_{n}\sim \mathcal {N}(0,1)$
, we have
This is best-possible in general (for example,
![]() $\Pr [|Z_{1}^{2}|\le \varepsilon ]$
scales like
$\Pr [|Z_{1}^{2}|\le \varepsilon ]$
scales like
![]() $\sqrt {\varepsilon }$
as
$\sqrt {\varepsilon }$
as
![]() $\varepsilon \to 0$
). However, we are able to prove (in Section 5) an optimal bound of the form
$\varepsilon \to 0$
). However, we are able to prove (in Section 5) an optimal bound of the form
![]() $O(\varepsilon /\sigma (f))$
in the case where the degree-2 part of f robustly has rank at least 3, in the sense of low-rank approximation (i.e., in the case where the degree-2 part of f is not close, in FrobeniusFootnote 3 norm, to a quadratic form of rank at most
$O(\varepsilon /\sigma (f))$
in the case where the degree-2 part of f robustly has rank at least 3, in the sense of low-rank approximation (i.e., in the case where the degree-2 part of f is not close, in FrobeniusFootnote 3 norm, to a quadratic form of rank at most
![]() $2$
).
$2$
).
Theorem 1.6. Let
![]() $\vec Z = (Z_1,\ldots ,Z_n)\sim \mathcal {N}(0,1)^{\otimes n}$
be a vector of independent standard Gaussian random variables. Consider a real quadratic polynomial
$\vec Z = (Z_1,\ldots ,Z_n)\sim \mathcal {N}(0,1)^{\otimes n}$
be a vector of independent standard Gaussian random variables. Consider a real quadratic polynomial
![]() $f(\vec Z)$
of
$f(\vec Z)$
of
![]() $\vec Z$
, which we may write as
$\vec Z$
, which we may write as
for some nonzero symmetric matrix
![]() $F\in \mathbb {R}^{n\times n}$
, some vector
$F\in \mathbb {R}^{n\times n}$
, some vector
![]() $\vec f\in \mathbb {R}^n$
and some
$\vec f\in \mathbb {R}^n$
and some
![]() $f_0\in \mathbb {R}$
. Suppose that for some
$f_0\in \mathbb {R}$
. Suppose that for some
![]() $\eta>0$
we have
$\eta>0$
we have
 $$\begin{align*}\min_{\substack{\widetilde F\in\mathbb{R}^{n\times n}\\ \operatorname{rank}(\widetilde F)\le 2}}\frac{\|F-\widetilde F\|^2_{\mathrm F}}{\|F\|^2_{\mathrm{F}}}\ge \eta. \end{align*}$$
$$\begin{align*}\min_{\substack{\widetilde F\in\mathbb{R}^{n\times n}\\ \operatorname{rank}(\widetilde F)\le 2}}\frac{\|F-\widetilde F\|^2_{\mathrm F}}{\|F\|^2_{\mathrm{F}}}\ge \eta. \end{align*}$$
Then for any
![]() $\varepsilon> 0$
we have
$\varepsilon> 0$
we have
for some
![]() $C_{\eta }$
depending on
$C_{\eta }$
depending on
![]() $\eta $
.
$\eta $
.
We remark that our robust-rank-3 assumption is best-possible, in the sense that this stronger bound may fail for quadratic forms with robust rank
![]() $2$
; for example,
$2$
; for example,
![]() $Z_{1}^{2}-Z_{2}^{2}$
has standard deviation
$Z_{1}^{2}-Z_{2}^{2}$
has standard deviation
![]() $2$
, and one can compute that
$2$
, and one can compute that
![]() $\Pr [|Z_{1}^{2}-Z_{2}^{2}|\le \varepsilon ]$
scales like
$\Pr [|Z_{1}^{2}-Z_{2}^{2}|\le \varepsilon ]$
scales like
![]() $\varepsilon \log (1/\varepsilon )$
as
$\varepsilon \log (1/\varepsilon )$
as
![]() $\varepsilon \to 0$
.
$\varepsilon \to 0$
.
We also remark that Theorem 1.6 can be interpreted as a kind of inverse theorem or structure theorem: the only way for
![]() $f(\vec Z)$
to exhibit atypical small-ball behavior is for f to be close to a low-rank quadratic form (c.f. inverse theorems for the Littlewood–Offord problem [Reference Tao and Vu92, Reference Nguyen and Vu78, Reference Tao and Vu91, Reference Rudelson and Vershynin87, Reference Nguyen77, Reference Nguyen and Vu79, Reference Kwan and Sauermann65]). It is also worth mentioning a different structure theorem due to Kane [Reference Kane61], showing that all bounded-degree polynomials of Gaussian random variables can be, in a certain sense, ‘decomposed’ into a small number of parts with typical small-ball behavior.
$f(\vec Z)$
to exhibit atypical small-ball behavior is for f to be close to a low-rank quadratic form (c.f. inverse theorems for the Littlewood–Offord problem [Reference Tao and Vu92, Reference Nguyen and Vu78, Reference Tao and Vu91, Reference Rudelson and Vershynin87, Reference Nguyen77, Reference Nguyen and Vu79, Reference Kwan and Sauermann65]). It is also worth mentioning a different structure theorem due to Kane [Reference Kane61], showing that all bounded-degree polynomials of Gaussian random variables can be, in a certain sense, ‘decomposed’ into a small number of parts with typical small-ball behavior.
Finally, we remark that it would be interesting to investigate extensions of Theorem 1.6 to higher-degree polynomials. Our proof uses diagonalization of quadratic forms in a crucial way, and new ideas would therefore be required (the ideas in the aforementioned paper of Kane [Reference Kane61] may be relevant).
1.2.3 Rank of Ramsey graphs
In order to actually apply Theorem 1.6, we need to use the fact that Ramsey graphs have adjacency matrices which robustly have high rank. A version of this fact was first observed by the first and third authors [Reference Kwan and Sauermann65], but we will need a much stronger version involving a partition into submatrices (Lemma 10.1). We believe that the connection between rank and homogeneous sets is of very general interest: For example, the celebrated log-rank conjecture in communication complexity has an equivalent formulation (due to Nisan and Wigderson [Reference Nisan and Wigderson80]) stating that a zero-one matrix with no large ‘homogeneous rectangle’ must have high rank. As part of our study of the rank of Ramsey graphs, we prove (Proposition 10.2) that binary matrices which are close to a low-rank real matrix are also close to a low-rank binary matrix. This may be of independent interest.
1.2.4 Switchings via moments
It turns out that in the setting of Theorem 1.2, Fourier-analytic estimates (in combination with the previously mentioned ideas) can only take us so far: For a C-Ramsey graph, we can roughly estimate the probability that
![]() $e(G[U])$
falls in a given short interval (whose length depends only on C), but not the probability that
$e(G[U])$
falls in a given short interval (whose length depends only on C), but not the probability that
![]() $e(G[U])$
is equal to a particular value. To obtain such precise control, we make use of the switching method, studying small perturbations to our random set U.
$e(G[U])$
is equal to a particular value. To obtain such precise control, we make use of the switching method, studying small perturbations to our random set U.
Roughly speaking, the switching method works as follows. To estimate the relative probabilities of events
![]() $\mathcal {A}$
and
$\mathcal {A}$
and
![]() $\mathcal {B}$
, one designs an appropriate ‘switching’ operation that takes outcomes satisfying
$\mathcal {B}$
, one designs an appropriate ‘switching’ operation that takes outcomes satisfying
![]() $\mathcal {A}$
to outcomes satisfying
$\mathcal {A}$
to outcomes satisfying
![]() $\mathcal {B}$
. One then obtains the desired estimate via upper and lower bounds on the number of ways to switch from an outcome satisfying
$\mathcal {B}$
. One then obtains the desired estimate via upper and lower bounds on the number of ways to switch from an outcome satisfying
![]() $\mathcal {A}$
, and the number of ways to switch to an outcome satisfying
$\mathcal {A}$
, and the number of ways to switch to an outcome satisfying
![]() $\mathcal {B}$
. This deceptively simple-sounding method has been enormously influential in combinatorial enumeration and the study of discrete random structures, and a variety of more sophisticated variations (considering more than two events) have been considered; see [Reference Hasheminezhad and McKay58, Reference Fack and McKay40] and the references therein.
$\mathcal {B}$
. This deceptively simple-sounding method has been enormously influential in combinatorial enumeration and the study of discrete random structures, and a variety of more sophisticated variations (considering more than two events) have been considered; see [Reference Hasheminezhad and McKay58, Reference Fack and McKay40] and the references therein.
In our particular situation (where we are switching between different possibilities of the set U), it does not seem to be possible to define a simple switching operation which has a controllable effect on
![]() $e(G[U])$
and for which we can obtain uniform upper and lower bounds on the number of ways to perform a switch. Instead, we introduce an averaged version of the switching method. Roughly speaking, we define random variables that measure the number of ways to switch between two classes and study certain moments of these random variables. We believe this idea may have other applications.
$e(G[U])$
and for which we can obtain uniform upper and lower bounds on the number of ways to perform a switch. Instead, we introduce an averaged version of the switching method. Roughly speaking, we define random variables that measure the number of ways to switch between two classes and study certain moments of these random variables. We believe this idea may have other applications.
1.3 Notation
We use standard asymptotic notation throughout, as follows. For functions
![]() $f=f(n)$
and
$f=f(n)$
and
![]() $g=g(n)$
, we write
$g=g(n)$
, we write
![]() $f=O(g)$
or
$f=O(g)$
or
![]() $f \lesssim g$
to mean that there is a constant C such that
$f \lesssim g$
to mean that there is a constant C such that
![]() $|f(n)|\le C|g(n)|$
for sufficiently large n. Similarly, we write
$|f(n)|\le C|g(n)|$
for sufficiently large n. Similarly, we write
![]() $f=\Omega (g)$
or
$f=\Omega (g)$
or
![]() $f \gtrsim g$
to mean that there is a constant
$f \gtrsim g$
to mean that there is a constant
![]() $c>0$
such that
$c>0$
such that
![]() $f(n)\ge c|g(n)|$
for sufficiently large n. Finally, we write
$f(n)\ge c|g(n)|$
for sufficiently large n. Finally, we write
![]() $f\asymp g$
or
$f\asymp g$
or
![]() $f=\Theta (g)$
to mean that
$f=\Theta (g)$
to mean that
![]() $f\lesssim g$
and
$f\lesssim g$
and
![]() $g\lesssim f$
, and we write
$g\lesssim f$
, and we write
![]() $f=o(g)$
or
$f=o(g)$
or
![]() $g=\omega (f)$
to mean that
$g=\omega (f)$
to mean that
![]() $f(n)/g(n)\to 0$
as
$f(n)/g(n)\to 0$
as
![]() $n\to \infty $
. Subscripts on asymptotic notation indicate quantities that should be treated as constants.
$n\to \infty $
. Subscripts on asymptotic notation indicate quantities that should be treated as constants.
We also use standard graph-theoretic notation. In particular,
![]() $V(G)$
and
$V(G)$
and
![]() $E(G)$
denote the vertex set of a graph G, and
$E(G)$
denote the vertex set of a graph G, and
![]() $e(G)=|E(G)|$
denotes the numbers of vertices and edges. We write
$e(G)=|E(G)|$
denotes the numbers of vertices and edges. We write
![]() $G[U]$
to denote the subgraph induced by a set of vertices
$G[U]$
to denote the subgraph induced by a set of vertices
![]() $U\subseteq V(G)$
. For a vertex
$U\subseteq V(G)$
. For a vertex
![]() $v\in V(G)$
, its neighborhood (i.e., the set of vertices adjacent to v) is denoted by
$v\in V(G)$
, its neighborhood (i.e., the set of vertices adjacent to v) is denoted by
![]() $N_G(v)$
, and its degree is denoted
$N_G(v)$
, and its degree is denoted
![]() $\deg _G(v)=|N_G(v)|$
(the subscript G will be omitted when it is clear from context). We also write
$\deg _G(v)=|N_G(v)|$
(the subscript G will be omitted when it is clear from context). We also write
![]() $N_U(v)=U\cap N(v)$
and
$N_U(v)=U\cap N(v)$
and
![]() $\deg _U(v)=|N_U(v)|$
to denote the degree of v into a vertex set U.
$\deg _U(v)=|N_U(v)|$
to denote the degree of v into a vertex set U.
Regarding probabilistic notation, we write
![]() $\mathcal N(\mu ,\sigma ^2)$
for the Gaussian distribution with mean
$\mathcal N(\mu ,\sigma ^2)$
for the Gaussian distribution with mean
![]() $\mu $
and variance
$\mu $
and variance
![]() $\sigma ^2$
. As usual, we call a random variable with distribution
$\sigma ^2$
. As usual, we call a random variable with distribution
![]() $\mathcal N(0,1)$
a standard Gaussian and we write
$\mathcal N(0,1)$
a standard Gaussian and we write
![]() $\mathcal N(0,1)^{\otimes n}$
for the distribution of a sequence of n independent standard Gaussian variables. For a real random variable X, we write
$\mathcal N(0,1)^{\otimes n}$
for the distribution of a sequence of n independent standard Gaussian variables. For a real random variable X, we write
![]() $\varphi _X\colon t\mapsto \mathbb {E}e^{itX}$
for the characteristic function of X. Though less standard, it is also convenient to write
$\varphi _X\colon t\mapsto \mathbb {E}e^{itX}$
for the characteristic function of X. Though less standard, it is also convenient to write
![]() $\sigma (X) = \sqrt {\operatorname {Var}X}$
for the standard deviation of X.
$\sigma (X) = \sqrt {\operatorname {Var}X}$
for the standard deviation of X.
We also collect some miscellaneous bits of notation. We use notation like
![]() $\vec {x}$
to denote (column) vectors and write
$\vec {x}$
to denote (column) vectors and write
![]() $\vec x_I$
for the restriction of a vector
$\vec x_I$
for the restriction of a vector
![]() $\vec x$
to the set I. We also write
$\vec x$
to the set I. We also write
![]() $M[I\!\times \!J]$
to denote the
$M[I\!\times \!J]$
to denote the
![]() $I\times J$
submatrix of a matrix M. For
$I\times J$
submatrix of a matrix M. For
![]() $r\in \mathbb {R}$
, we write
$r\in \mathbb {R}$
, we write
![]() $\lVert r\rVert _{\mathbb {R}/\mathbb {Z}}$
to denote the distance of r to the closest integer, and for an integer
$\lVert r\rVert _{\mathbb {R}/\mathbb {Z}}$
to denote the distance of r to the closest integer, and for an integer
![]() $n\in \mathbb {N}$
, we write
$n\in \mathbb {N}$
, we write
![]() $[n]=\{1,\ldots ,n\}$
. All logarithms in this paper without an explicit base are to base e, and the set of natural numbers
$[n]=\{1,\ldots ,n\}$
. All logarithms in this paper without an explicit base are to base e, and the set of natural numbers
![]() $\mathbb N$
includes zero.
$\mathbb N$
includes zero.
2 Short deductions
We now present the short deductions of Theorems 1.1 and 1.5 from Theorem 1.2.
Proof of Theorem 1.1 assuming Theorem 1.2
As mentioned in the introduction, Alon, Krivelevich and Sudakov [Reference Alon, Krivelevich and Sudakov8, Theorem 1.1] proved that there is some
![]() $\alpha =\alpha (C)>0$
such that the conclusion of Theorem 1.1 holds for all
$\alpha =\alpha (C)>0$
such that the conclusion of Theorem 1.1 holds for all
![]() $0\leq x\leq n^{\alpha }$
.
$0\leq x\leq n^{\alpha }$
.
Fix
![]() $0<\lambda <1/2$
with
$0<\lambda <1/2$
with
![]() $(1-\lambda )^2\ge 1-\eta $
, and let
$(1-\lambda )^2\ge 1-\eta $
, and let
![]() $p=1-\lambda $
. It now suffices to prove the desired statement for
$p=1-\lambda $
. It now suffices to prove the desired statement for
![]() $n^{\alpha }\leq x\leq p^2 e(G)$
, so consider such an integer x. Let us identify the vertex set of G with
$n^{\alpha }\leq x\leq p^2 e(G)$
, so consider such an integer x. Let us identify the vertex set of G with
![]() $\{1,\ldots ,n\}$
. We can find some
$\{1,\ldots ,n\}$
. We can find some
![]() $m\in \{1,\ldots ,n\}$
such that
$m\in \{1,\ldots ,n\}$
such that
![]() $e(G[\{1,\ldots ,m\}])\geq x/p^2\geq e(G[\{1,\ldots ,m-1\}])$
. Let
$e(G[\{1,\ldots ,m\}])\geq x/p^2\geq e(G[\{1,\ldots ,m-1\}])$
. Let
![]() $G'$
denote the induced subgraph of G on the vertex set
$G'$
denote the induced subgraph of G on the vertex set
![]() $\{1,\ldots ,m\}$
, and note that
$\{1,\ldots ,m\}$
, and note that
Hence,
![]() $|x-p^2e(G')|\leq p^2m\leq m^{3/2}$
. As
$|x-p^2e(G')|\leq p^2m\leq m^{3/2}$
. As
![]() $m^2\geq e(G')\geq x/p^2\geq n^{\alpha }$
, we have
$m^2\geq e(G')\geq x/p^2\geq n^{\alpha }$
, we have
![]() $m\geq n^{\alpha /2}$
and therefore
$m\geq n^{\alpha /2}$
and therefore
![]() $G'$
is a
$G'$
is a
![]() $(2C/\alpha )$
-Ramsey graph. Thus, for a random subset U of
$(2C/\alpha )$
-Ramsey graph. Thus, for a random subset U of
![]() $V(G')=\{1,\ldots ,m\}$
that includes each vertex of
$V(G')=\{1,\ldots ,m\}$
that includes each vertex of
![]() $G'$
with probability p, by Theorem 1.2 (with
$G'$
with probability p, by Theorem 1.2 (with
![]() $A=1$
) we have
$A=1$
) we have
![]() $e(G[U])=e(G'[U])=x$
with probability
$e(G[U])=e(G'[U])=x$
with probability
![]() $\Omega _{C,\lambda }(m^{-3/2})$
. In particular, if n and therefore m is sufficiently large with respect to
$\Omega _{C,\lambda }(m^{-3/2})$
. In particular, if n and therefore m is sufficiently large with respect to
![]() $C,\lambda $
, then there exists a subset
$C,\lambda $
, then there exists a subset
![]() $U\subseteq V(G')\subseteq V(G)$
with
$U\subseteq V(G')\subseteq V(G)$
with
![]() $e(G[U])=e(G'[U])=x$
.
$e(G[U])=e(G'[U])=x$
.
Proof of Theorem 1.5 assuming Theorem 1.2
We may assume that n is sufficiently large with respect to C and
![]() $\lambda $
(noting that the statement is trivially true for
$\lambda $
(noting that the statement is trivially true for
![]() $n\le K$
). Let U be a random subset of
$n\le K$
). Let U be a random subset of
![]() $V(G)$
obtained by including each vertex with probability
$V(G)$
obtained by including each vertex with probability
![]() $k/n$
independently (recalling that Theorem 1.5 concerns a random set W of exactly k vertices). A direct computation using Stirling’s formula shows that
$k/n$
independently (recalling that Theorem 1.5 concerns a random set W of exactly k vertices). A direct computation using Stirling’s formula shows that
![]() $\Pr [|U|=k]\gtrsim _{\lambda } 1/\sqrt n$
, so for each
$\Pr [|U|=k]\gtrsim _{\lambda } 1/\sqrt n$
, so for each
![]() $x\in \mathbb Z$
, Theorem 1.2 yields
$x\in \mathbb Z$
, Theorem 1.2 yields
It turns out that in order to prove Theorem 1.2, it essentially suffices to consider the case
![]() $p=1/2$
, as long as we permit some ‘linear terms’. Specifically, instead of considering random variable
$p=1/2$
, as long as we permit some ‘linear terms’. Specifically, instead of considering random variable
![]() $e(G[U])$
we need to consider a random variable of the form
$e(G[U])$
we need to consider a random variable of the form
![]() $X = e(G[U]) + \sum _{v\in U}e_v+e_0$
, as in the following theorem.Footnote 4
$X = e(G[U]) + \sum _{v\in U}e_v+e_0$
, as in the following theorem.Footnote 4
Theorem 2.1. Fix
![]() $C,H> 0$
. Let G be a C-Ramsey graph with n vertices, and consider
$C,H> 0$
. Let G be a C-Ramsey graph with n vertices, and consider
![]() $e_0\in \mathbb Z$
and a vector
$e_0\in \mathbb Z$
and a vector
![]() $\vec {e}\in \mathbb {Z}^{V(G)}$
with
$\vec {e}\in \mathbb {Z}^{V(G)}$
with
![]() $0\le e_v\le Hn$
for all
$0\le e_v\le Hn$
for all
![]() $v\in V(G)$
. Let
$v\in V(G)$
. Let
![]() $U\subseteq V(G)$
be a random vertex subset obtained by including each vertex with probability
$U\subseteq V(G)$
be a random vertex subset obtained by including each vertex with probability
![]() $1/2$
independently, and let
$1/2$
independently, and let
![]() $X = e(G[U]) + \sum _{v\in U}e_v+e_0$
. Then
$X = e(G[U]) + \sum _{v\in U}e_v+e_0$
. Then
and for every fixed
![]() $A> 0$
,
$A> 0$
,
 $$\begin{align*}\inf_{\substack{x\in\mathbb{Z}\\|x-\mathbb E X|\le An^{3/2}}}\Pr[X=x]\gtrsim_{C,H,A}n^{-3/2}.\end{align*}$$
$$\begin{align*}\inf_{\substack{x\in\mathbb{Z}\\|x-\mathbb E X|\le An^{3/2}}}\Pr[X=x]\gtrsim_{C,H,A}n^{-3/2}.\end{align*}$$
This theorem implies Theorem 1.2 (which also allows for a sampling probability
![]() $p\ne 1/2$
), as we show next. The rest of the paper will be devoted to proving Theorem 2.1.
$p\ne 1/2$
), as we show next. The rest of the paper will be devoted to proving Theorem 2.1.
Proof of Theorem 1.2 assuming Theorem 2.1
We may assume that n is sufficiently large with respect to C and
![]() $\lambda $
. We proceed slightly differently depending on whether
$\lambda $
. We proceed slightly differently depending on whether
![]() $p\le 1/2$
or
$p\le 1/2$
or
![]() $p>1/2$
.
$p>1/2$
.
Case 1:
![]() $p\le 1/2$
. In this case, we can realize the distribution of U by first taking a random subset
$p\le 1/2$
. In this case, we can realize the distribution of U by first taking a random subset
![]() $U_0$
in which every vertex is present with probability
$U_0$
in which every vertex is present with probability
![]() $2p$
and then considering a random subset
$2p$
and then considering a random subset
![]() $U\subseteq U_0$
in which every vertex in
$U\subseteq U_0$
in which every vertex in
![]() $U_0$
is present with probability
$U_0$
is present with probability
![]() $1/2$
. By a Chernoff bound, we have
$1/2$
. By a Chernoff bound, we have
![]() $|U_0|\ge pn\ge \lambda n$
with probability
$|U_0|\ge pn\ge \lambda n$
with probability
![]() $1-o_{\lambda }(n^{-3/2})$
, in which case
$1-o_{\lambda }(n^{-3/2})$
, in which case
![]() $G[U_0]$
is a
$G[U_0]$
is a
![]() $(2C)$
-Ramsey graph. We may thus condition on such an outcome of
$(2C)$
-Ramsey graph. We may thus condition on such an outcome of
![]() $U_0$
. By Theorem 2.1, the conditional probability of the event
$U_0$
. By Theorem 2.1, the conditional probability of the event
![]() $X=x$
is at most
$X=x$
is at most
![]() $O_{C}(|U_0|^{-3/2})\lesssim _{C,\lambda }n^{-3/2}$
, proving the desired upper bound.
$O_{C}(|U_0|^{-3/2})\lesssim _{C,\lambda }n^{-3/2}$
, proving the desired upper bound.
For the lower bound, first note that
![]() $e(G[U_0])$
has expectation
$e(G[U_0])$
has expectation
![]() $(2p)^2e(G)$
and variance
$(2p)^2e(G)$
and variance
![]() (note that there are at most
(note that there are at most
![]() $n^3$
nonzero summands since the summands for distinct
$n^3$
nonzero summands since the summands for distinct
![]() $u,v,w,z$
are zero). Hence, by Chebyshev’s inequality and a Chernoff bound, with probability at least
$u,v,w,z$
are zero). Hence, by Chebyshev’s inequality and a Chernoff bound, with probability at least
![]() $1/2$
the outcome of
$1/2$
the outcome of
![]() $U_0$
satisfies
$U_0$
satisfies
![]() $|e(G[U_0])-(2p)^2e(G)|\le 2n^{3/2}$
and
$|e(G[U_0])-(2p)^2e(G)|\le 2n^{3/2}$
and
![]() $|U_0|\ge \lambda n$
. Conditioning on such an outcome of
$|U_0|\ge \lambda n$
. Conditioning on such an outcome of
![]() $U_0$
, the lower bound in Theorem 1.2 follows from the lower bound in Theorem 2.1 applied to
$U_0$
, the lower bound in Theorem 1.2 follows from the lower bound in Theorem 2.1 applied to
![]() $G[U_0]$
(noting that
$G[U_0]$
(noting that
![]() $x\in \mathbb {Z}$
with
$x\in \mathbb {Z}$
with
![]() $|x-p^2e(G)|\le An^{3/2}$
differs from
$|x-p^2e(G)|\le An^{3/2}$
differs from
![]() $\mathbb {E}[e(G[U])|U_0] = e(G[U_0])/4$
by at most
$\mathbb {E}[e(G[U])|U_0] = e(G[U_0])/4$
by at most
![]() $(A+1)n^{3/2}\le (A+1)/\lambda ^3\cdot |U_0|^{3/2}$
).
$(A+1)n^{3/2}\le (A+1)/\lambda ^3\cdot |U_0|^{3/2}$
).
Case 2:
![]() $p> 1/2$
. In this case, we can realize the distribution of U by first taking a random subset
$p> 1/2$
. In this case, we can realize the distribution of U by first taking a random subset
![]() $U_0$
in which every vertex is present with probability
$U_0$
in which every vertex is present with probability
![]() $2p-1$
and then considering a random superset
$2p-1$
and then considering a random superset
![]() $U\supseteq U_0$
in which every vertex outside
$U\supseteq U_0$
in which every vertex outside
![]() $U_0$
is present with probability
$U_0$
is present with probability
![]() $1/2$
.
$1/2$
.
By a Chernoff bound, we have
![]() $|V(G)\setminus U_0|\ge (1-p)n\ge \lambda n$
with probability
$|V(G)\setminus U_0|\ge (1-p)n\ge \lambda n$
with probability
![]() $1-o_{\lambda }(n^{-3/2})$
, in which case
$1-o_{\lambda }(n^{-3/2})$
, in which case
![]() $G[V(G)\setminus U_0]$
is a
$G[V(G)\setminus U_0]$
is a
![]() $(2C)$
-Ramsey graph. Conditioning on such an outcome of
$(2C)$
-Ramsey graph. Conditioning on such an outcome of
![]() $U_0$
, the upper bound in Theorem 1.2 follows from the upper bound in Theorem 2.1 applied to
$U_0$
, the upper bound in Theorem 1.2 follows from the upper bound in Theorem 2.1 applied to
![]() $G[V(G)\setminus U_0]$
(where now we take
$G[V(G)\setminus U_0]$
(where now we take
![]() $e_0=e(G[U_0])$
and
$e_0=e(G[U_0])$
and
![]() $e_v=\deg _{U_0}(v)$
for each
$e_v=\deg _{U_0}(v)$
for each
![]() $v\in V(G)\setminus U_0$
and
$v\in V(G)\setminus U_0$
and
![]() $H=1/\lambda $
).
$H=1/\lambda $
).
For the lower bound, observe that
![]() $\mathbb {E}[e(G[U])|U_0]=e(G[U_0])+e(V(G)\setminus U_0,U_0)/2+e(G[V(G)\setminus U_0])/4$
has expectation
$\mathbb {E}[e(G[U])|U_0]=e(G[U_0])+e(V(G)\setminus U_0,U_0)/2+e(G[V(G)\setminus U_0])/4$
has expectation
![]() $\mathbb {E}e(G[U])=p^2e(G)$
and variance at most
$\mathbb {E}e(G[U])=p^2e(G)$
and variance at most
![]() $n^3$
(by a similar calculation as in Case 1). Thus, by Chebyshev’s inequality and a Chernoff bound with probability at least
$n^3$
(by a similar calculation as in Case 1). Thus, by Chebyshev’s inequality and a Chernoff bound with probability at least
![]() $1/2$
the outcome of
$1/2$
the outcome of
![]() $U_0$
satisfies
$U_0$
satisfies
![]() $|\mathbb {E}[e(G[U])|U_0]-p^2e(G)|\le 2n^{3/2}$
and
$|\mathbb {E}[e(G[U])|U_0]-p^2e(G)|\le 2n^{3/2}$
and
![]() $|V(G)\setminus U_0|\ge \lambda n$
. Conditioning on such an outcome of
$|V(G)\setminus U_0|\ge \lambda n$
. Conditioning on such an outcome of
![]() $U_0$
, the lower bound in Theorem 1.2 follows from the lower bound in Theorem 2.1 applied to
$U_0$
, the lower bound in Theorem 1.2 follows from the lower bound in Theorem 2.1 applied to
![]() $G[V(G)\setminus U_0]$
(again taking
$G[V(G)\setminus U_0]$
(again taking
![]() $e_0=e(G[U_0])$
and
$e_0=e(G[U_0])$
and
![]() $e_v=\deg _{U_0}(v)$
for each
$e_v=\deg _{U_0}(v)$
for each
![]() $v\in V(G)\setminus U_0$
and
$v\in V(G)\setminus U_0$
and
![]() $H=1/\lambda $
and observing that
$H=1/\lambda $
and observing that
![]() $|x-\mathbb {E}[e(G[U])|U_0]|\le (A+2)/\lambda ^3\cdot |V(G)\setminus U_0|^{3/2}$
).
$|x-\mathbb {E}[e(G[U])|U_0]|\le (A+2)/\lambda ^3\cdot |V(G)\setminus U_0|^{3/2}$
).
3 Proof discussion and outline
In the previous section, we saw how all of our results stated in the introduction follow from Theorem 2.1. Here, we discuss the high-level ideas of the proof of Theorem 2.1, and the obstacles that must be overcome. Afterwards, we will outline the organization of the rest of the paper.
3.1 Central limit theorems at multiple scales
As mentioned in the introduction, our starting point is the possibility that a local central limit theorem might hold for the random variable
![]() $X=e(G[U])+\sum _{v\in U} e_v+e_0$
in Theorem 2.1. However, some further thought reveals that such a theorem cannot hold in general. To appreciate this, it is illuminating to rewrite X in the so-called Fourier–Walsh basis: Define
$X=e(G[U])+\sum _{v\in U} e_v+e_0$
in Theorem 2.1. However, some further thought reveals that such a theorem cannot hold in general. To appreciate this, it is illuminating to rewrite X in the so-called Fourier–Walsh basis: Define
![]() $\vec {x}\in \{-1,1\}^{V(G)}$
by taking
$\vec {x}\in \{-1,1\}^{V(G)}$
by taking
![]() $x_{v}=1$
if
$x_{v}=1$
if
![]() $v\in U$
, and
$v\in U$
, and
![]() $x_{v}=-1$
if
$x_{v}=-1$
if
![]() $v\notin U$
. Then, we have
$v\notin U$
. Then, we have
 $$ \begin{align} X = \mathbb{E}X + \frac{1}{2}\sum_{v\in V(G)}\left(e_{v}+\frac{1}{2}\deg_{G}(v)\right)x_{v} + \frac{1}{4}\sum_{uv\in E(G)}x_{u}x_{v}. \end{align} $$
$$ \begin{align} X = \mathbb{E}X + \frac{1}{2}\sum_{v\in V(G)}\left(e_{v}+\frac{1}{2}\deg_{G}(v)\right)x_{v} + \frac{1}{4}\sum_{uv\in E(G)}x_{u}x_{v}. \end{align} $$
Writing
![]() $L=\frac {1}{2}\sum _{v\in V(G)}\left (e_{v}+\frac {1}{2}\deg _{G}(v)\right )x_{v}$
and
$L=\frac {1}{2}\sum _{v\in V(G)}\left (e_{v}+\frac {1}{2}\deg _{G}(v)\right )x_{v}$
and
![]() $Q=\frac {1}{4}\sum _{uv\in E(G)}x_{u}x_{v}$
, we have
$Q=\frac {1}{4}\sum _{uv\in E(G)}x_{u}x_{v}$
, we have
![]() $X=\mathbb {E}X+L+Q$
. Essentially, we have isolated the ‘linear part’ L and the ‘quadratic part’ Q of the random variable X, in such a way that the covariance between L and Q is zero. It turns out that L typically dominates the large-scale behavior of X: The variance of L is always of order
$X=\mathbb {E}X+L+Q$
. Essentially, we have isolated the ‘linear part’ L and the ‘quadratic part’ Q of the random variable X, in such a way that the covariance between L and Q is zero. It turns out that L typically dominates the large-scale behavior of X: The variance of L is always of order
![]() $n^{3}$
, whereas the variance of Q is only of order
$n^{3}$
, whereas the variance of Q is only of order
![]() $n^{2}$
. It is easy to show that L satisfies a central limit theorem (being a sum of independent random variables). However, this central limit theorem may break down at small scales: For example, it is possible that in G, every vertex has degree exactly
$n^{2}$
. It is easy to show that L satisfies a central limit theorem (being a sum of independent random variables). However, this central limit theorem may break down at small scales: For example, it is possible that in G, every vertex has degree exactly
![]() $n/2$
, in which case (for
$n/2$
, in which case (for
![]() $\vec {e}=\vec 0$
) the linear part L only takes values in the lattice
$\vec {e}=\vec 0$
) the linear part L only takes values in the lattice
![]() $(n/8)\mathbb {Z}$
.
$(n/8)\mathbb {Z}$
.
In this
![]() $(n/2)$
-regular case (with
$(n/2)$
-regular case (with
![]() $\vec {e}=\vec 0$
), we might hope to prove Theorem 2.1 in two stages: Having shown that L satisfies a central limit theorem, we might hope to show that Q satisfies a local central limit theorem after conditioning on an outcome of L (in this case, revealing L only reveals the number of vertices in our random set U, so there is still plenty of randomness remaining for Q).
$\vec {e}=\vec 0$
), we might hope to prove Theorem 2.1 in two stages: Having shown that L satisfies a central limit theorem, we might hope to show that Q satisfies a local central limit theorem after conditioning on an outcome of L (in this case, revealing L only reveals the number of vertices in our random set U, so there is still plenty of randomness remaining for Q).
If this strategy were to succeed, it would reveal that in this case the true distribution of X is Gaussian on two different scales: When ‘zoomed out’, we see a bell curve with standard deviation about
![]() $n^{3/2}$
, but ‘zooming in’ reveals a superposition of many smaller bell curves each with standard deviation about n (see Figure 1). This kind of behavior can be described in terms of a so-called Jacobi theta function and has been observed in combinatorial settings before (by the second and fourth authors [Reference Sah and Sawhney88]).
$n^{3/2}$
, but ‘zooming in’ reveals a superposition of many smaller bell curves each with standard deviation about n (see Figure 1). This kind of behavior can be described in terms of a so-called Jacobi theta function and has been observed in combinatorial settings before (by the second and fourth authors [Reference Sah and Sawhney88]).
3.2 An additive structure dichotomy
There are a few problems with the above plan. When G is regular, we have the very special property that revealing L only reveals the number of vertices in U (after which U is a uniformly random vertex set of this revealed size). There are many available tools to study random sets of fixed size (this setting is often called the ‘Boolean slice’). However, in general, revealing L may result in a very complicated conditional distribution.
We handle this issue via an additive structure dichotomy, using the notion of regularized least common denominator (RLCD) introduced by Vershynin [Reference Vershynin95] in the context of random matrix theory (a ‘robust version’ of the notion of essential LCD previously introduced by Rudelson and Vershynin [Reference Rudelson and Vershynin87]). Roughly speaking, we consider the RLCD of the degree sequence of G. If this RLCD is small, then the degree sequence is ‘additively structured’ (as in our
![]() $(n/2)$
-regular example), which (as we prove in Lemma 4.12) has the consequence that the vertices of G can be divided into a small number of ‘buckets’ of vertices which have roughly the same coefficient in L (i.e,. the values of
$(n/2)$
-regular example), which (as we prove in Lemma 4.12) has the consequence that the vertices of G can be divided into a small number of ‘buckets’ of vertices which have roughly the same coefficient in L (i.e,. the values of
![]() $e_v+\deg _G(v)/2$
are roughly the same). This means that conditioning on the number of vertices of U inside each bucket is tantamount to conditioning on the approximate value of L (crucially, this conditioning dramatically reduces the variance), while the resulting conditional distribution is tractable to analyze.
$e_v+\deg _G(v)/2$
are roughly the same). This means that conditioning on the number of vertices of U inside each bucket is tantamount to conditioning on the approximate value of L (crucially, this conditioning dramatically reduces the variance), while the resulting conditional distribution is tractable to analyze.
On the other hand, if the RLCD is large, then the degree sequence is ‘additively unstructured’, and the linear part L is well mixing (satisfying a central limit theorem at scales polynomially smaller than n). In this case, it essentially is possibleFootnote 5 to prove a local central limit theorem for X (this is the easier of the two cases of the additive structure dichotomy). Concretely, an example of this case is when G is a typical outcome of an inhomogeneous random graph on the vertex set
![]() $\{m/4,\ldots ,3m/4\}$
, where each edge
$\{m/4,\ldots ,3m/4\}$
, where each edge
![]() $ij$
is present with probability
$ij$
is present with probability
![]() $i\cdot j/m^{2}$
independently.
$i\cdot j/m^{2}$
independently.
3.3 Breakdown of Gaussian behavior
Recall from the previous subsection that in the ‘additively structured’ case, we study the distribution of
![]() $e(G[U])$
after conditioning on the sizes of the intersections of U with our ‘buckets’ of vertices (which, morally speaking, corresponds to ‘conditioning on the approximate value of L’). It turns out that even after this conditioning, a local central limit theorem may still fail to hold, in quite a dramatic way: It can happen that, conditionally, no central limit theorem holds at all (meaning that when we ‘zoom in’ we do not see bell curves but some completely different shapes). For example, if G is a typical outcome of two independent disjoint copies of the Erdős–Rényi random graph
$e(G[U])$
after conditioning on the sizes of the intersections of U with our ‘buckets’ of vertices (which, morally speaking, corresponds to ‘conditioning on the approximate value of L’). It turns out that even after this conditioning, a local central limit theorem may still fail to hold, in quite a dramatic way: It can happen that, conditionally, no central limit theorem holds at all (meaning that when we ‘zoom in’ we do not see bell curves but some completely different shapes). For example, if G is a typical outcome of two independent disjoint copies of the Erdős–Rényi random graph
![]() $\mathbb {G}(n/2,1/2)$
, then one may think of all vertices being in the same bucket, and one can show that the limiting distribution of
$\mathbb {G}(n/2,1/2)$
, then one may think of all vertices being in the same bucket, and one can show that the limiting distribution of
![]() $e(G[U])$
conditioned on the event
$e(G[U])$
conditioned on the event
![]() $|U|=n/2$
(up to translation and scaling) isFootnote 6 that of
$|U|=n/2$
(up to translation and scaling) isFootnote 6 that of
![]() $Z_{1}^{2}+2\sqrt {3}Z_{2}$
, where
$Z_{1}^{2}+2\sqrt {3}Z_{2}$
, where
![]() $Z_{1},Z_{2}$
are independent standard Gaussian random variables (see Figure 2).
$Z_{1},Z_{2}$
are independent standard Gaussian random variables (see Figure 2).

Figure 2 On the left, we obtain G as a disjoint union of two independent Erdős–Rényi random graphs
![]() $\mathbb G(800,0.96)$
, and we consider 500,000 independent samples of a uniformly random vertex subsets Uwith exactly 800 vertices. The resulting histogram for
$\mathbb G(800,0.96)$
, and we consider 500,000 independent samples of a uniformly random vertex subsets Uwith exactly 800 vertices. The resulting histogram for
![]() $e(G[U])$
may look approximately Gaussian, but closer inspection reveals asymmetry in the tails. This is not just an artifact of small numbers: The limiting distribution comes from a nontrivial quadratic polynomial of Gaussian random variables. Actually, it is possible for the skew to be much more exaggerated (the curve on the right shows one possibility for the limiting probability mass function of
$e(G[U])$
may look approximately Gaussian, but closer inspection reveals asymmetry in the tails. This is not just an artifact of small numbers: The limiting distribution comes from a nontrivial quadratic polynomial of Gaussian random variables. Actually, it is possible for the skew to be much more exaggerated (the curve on the right shows one possibility for the limiting probability mass function of
![]() $e(G[U])$
), but this is difficult to observe computationally, as this shape only really becomes visible for enormous graphs G.
$e(G[U])$
), but this is difficult to observe computationally, as this shape only really becomes visible for enormous graphs G.
In general, one can use a Gaussian invariance principle [Reference Mossel, O’Donnell and Oleszkiewicz74, Reference Filmus and Mossel43, Reference Filmus, Kindler, Mossel and Wimmer42] to show that the asymptotic conditional distribution of
![]() $e(G[U])$
always corresponds to some quadratic polynomial of Gaussian random variables (see also [Reference Bhattacharya, Mukherjee and Mukherjee15, Reference Bhattacharya, Das, Mukherjee and Mukherjee14]); instead of proving a local central limit theorem, we need to prove some type of local limit theorem for convergence to that distribution.
$e(G[U])$
always corresponds to some quadratic polynomial of Gaussian random variables (see also [Reference Bhattacharya, Mukherjee and Mukherjee15, Reference Bhattacharya, Das, Mukherjee and Mukherjee14]); instead of proving a local central limit theorem, we need to prove some type of local limit theorem for convergence to that distribution.
In order to prove a local limit theorem of this type, it is necessary to ensure that the limiting distribution (some quadratic polynomial of Gaussian random variables) is ‘well behaved’. This is where the tools discussed in Sections 1.2.2 and 1.2.3 come in: We prove that adjacency matrices of Ramsey graphs robustly have high rank, then apply certain variations of Theorem 1.6.
3.4 Controlling the characteristic function
We are now left with the task of actually proving the necessary local limit theorems. For this, we work in Fourier space, studying the characteristic functions
![]() $\varphi _{Y}\colon \tau \mapsto \mathbb {E}e^{i\tau Y}$
of certain random variables Y (namely, we need to consider both the random variable
$\varphi _{Y}\colon \tau \mapsto \mathbb {E}e^{i\tau Y}$
of certain random variables Y (namely, we need to consider both the random variable
![]() $X=e(G[U])+\sum _{v\in U} e_v+e_0$
and certain conditional random variables arising in the additively structured case). Our aim is to compare Y to an approximating random variable Z (where Z is either a Gaussian random variable or some quadratic polynomial of Gaussian random variables). This amounts to proving a suitable upper bound on
$X=e(G[U])+\sum _{v\in U} e_v+e_0$
and certain conditional random variables arising in the additively structured case). Our aim is to compare Y to an approximating random variable Z (where Z is either a Gaussian random variable or some quadratic polynomial of Gaussian random variables). This amounts to proving a suitable upper bound on
![]() $|\varphi _{Y}(\tau )-\varphi _{Z}(\tau )|$
, for as broad a range of
$|\varphi _{Y}(\tau )-\varphi _{Z}(\tau )|$
, for as broad a range of
![]() $\tau $
as possible (if one wants to precisely estimate point probabilities
$\tau $
as possible (if one wants to precisely estimate point probabilities
![]() $\Pr [Y=x]$
, it turns out that one needs to handle all
$\Pr [Y=x]$
, it turns out that one needs to handle all
![]() $\tau $
in the range
$\tau $
in the range
![]() $[-\pi ,\pi ]$
). We use different techniques for different ranges of
$[-\pi ,\pi ]$
). We use different techniques for different ranges of
![]() $\tau \in \mathbb {R}$
.
$\tau \in \mathbb {R}$
.
In the regime where
![]() $\tau $
is very small (e.g., when
$\tau $
is very small (e.g., when
![]() $|\tau |\le n^{0.01}/\sigma (Y)$
),
$|\tau |\le n^{0.01}/\sigma (Y)$
),
![]() $\varphi _{Y}(\tau )$
controls the large-scale distribution of Y, so depending on the setting we either employ standard techniques for proving central limit theorems or a Gaussian invariance principle.
$\varphi _{Y}(\tau )$
controls the large-scale distribution of Y, so depending on the setting we either employ standard techniques for proving central limit theorems or a Gaussian invariance principle.
For larger
![]() $\tau $
, it will be easy to show that our approximating characteristic function
$\tau $
, it will be easy to show that our approximating characteristic function
![]() $\varphi _{Z}(\tau )$
is exponentially small in absolute value, so estimating
$\varphi _{Z}(\tau )$
is exponentially small in absolute value, so estimating
![]() $|\varphi _{Y}(\tau )-\varphi _{Z}(\tau )|$
amounts to proving an upper bound on
$|\varphi _{Y}(\tau )-\varphi _{Z}(\tau )|$
amounts to proving an upper bound on
![]() $|\varphi _{Y}(\tau )|$
, exploiting cancellation in
$|\varphi _{Y}(\tau )|$
, exploiting cancellation in
![]() $\mathbb {E}e^{i\tau Y}$
as
$\mathbb {E}e^{i\tau Y}$
as
![]() $e^{i\tau Y}$
varies around the unit circle. Depending on the value of
$e^{i\tau Y}$
varies around the unit circle. Depending on the value of
![]() $\tau $
, we are able to exploit cancellation from either the ‘linear’ or the ‘quadratic’ part of Y.
$\tau $
, we are able to exploit cancellation from either the ‘linear’ or the ‘quadratic’ part of Y.
To exploit cancellation from the linear part, we adapt a decorrelation technique first introduced by Berkowitz [Reference Berkowitz12] to study clique counts in random graphs (see also [Reference Sah and Sawhney88]), involving a subsampling argument and a Taylor expansion. While all previous applications of this technique exploited the particular symmetries and combinatorial structure of a specific polynomial of interest, here we instead take advantage of the robustness inherent in the definition of RLCD. We hope that these types of ideas will be applicable to the study of even more general types of polynomials.
To exploit cancellation from the quadratic part, we use the method of decoupling, building on arguments of the first and third authors [Reference Kwan and Sauermann65]. Our improvements involve taking advantage of Fourier cancellation ‘on multiple scales’, which requires a sharpening of arguments of the first author and Sudakov [Reference Kwan and Sudakov67] (building on work of Bukh and Sudakov [Reference Bukh and Sudakov16]) concerning ‘richness’ of Ramsey graphs.
The relevant ideas for all the Fourier-analytic estimates discussed in this subsection will be discussed in more detail in the appropriate sections of the paper (Sections 7 and 8).
3.5 Pointwise control via switching
Unfortunately, it seems to be extremely difficult to study the cancellations in
![]() $\varphi _{X}(\tau )$
for very large
$\varphi _{X}(\tau )$
for very large
![]() $\tau $
, and we are only able to control the range where
$\tau $
, and we are only able to control the range where
![]() $|\tau |\le \nu $
for some small constant
$|\tau |\le \nu $
for some small constant
![]() $\nu =\nu (C)$
(recalling that G is C-Ramsey). As a consequence, the above ideas only prove the following weakening of Theorem 2.1 (where we control the probability of X lying in a constant-length interval instead of being equal to a particular value).
$\nu =\nu (C)$
(recalling that G is C-Ramsey). As a consequence, the above ideas only prove the following weakening of Theorem 2.1 (where we control the probability of X lying in a constant-length interval instead of being equal to a particular value).
Theorem 3.1. Fix
![]() $C> 0$
. There is
$C> 0$
. There is
![]() $B = B(C)> 0$
so the following holds for any fixed
$B = B(C)> 0$
so the following holds for any fixed
![]() $H>0$
. Let G be an C-Ramsey graph with n vertices, and consider
$H>0$
. Let G be an C-Ramsey graph with n vertices, and consider
![]() $e_0\in \mathbb {R}$
and a vector
$e_0\in \mathbb {R}$
and a vector
![]() $\vec {e}\in \mathbb {R}^{V(G)}$
with
$\vec {e}\in \mathbb {R}^{V(G)}$
with
![]() $0\le e_v\le Hn$
for all
$0\le e_v\le Hn$
for all
![]() $v\in V(G)$
. Let
$v\in V(G)$
. Let
![]() $U\subseteq V(G)$
be a random vertex subset obtained by including each vertex with probability
$U\subseteq V(G)$
be a random vertex subset obtained by including each vertex with probability
![]() $1/2$
independently, and let
$1/2$
independently, and let
![]() $X = e(G[U]) + \sum _{v\in U}e_v +e_0$
. Then
$X = e(G[U]) + \sum _{v\in U}e_v +e_0$
. Then
and for every fixed
![]() $A>0$
,
$A>0$
,
 $$\begin{align*}\inf_{\substack{x\in\mathbb{Z}\\|x-\mathbb E X|\le An^{3/2}}}\Pr[|X-x|\le B]\gtrsim_{C,H,A}n^{-3/2}.\end{align*}$$
$$\begin{align*}\inf_{\substack{x\in\mathbb{Z}\\|x-\mathbb E X|\le An^{3/2}}}\Pr[|X-x|\le B]\gtrsim_{C,H,A}n^{-3/2}.\end{align*}$$
Theorem 3.1 already implies the upper bound in Theorem 2.1 but not the lower bound. In Section 13, we deduce the desired lower bound on point probabilities from Theorem 3.1 (interestingly, this deduction requires both the lower and the upper bound in Theorem 3.1). As mentioned in the introduction, for this deduction, we introduce an ‘averaged’ version of the so-called switching method. In particular, for
![]() $\ell \in \{-B,\ldots ,B\}$
, we consider the pairs of vertices
$\ell \in \{-B,\ldots ,B\}$
, we consider the pairs of vertices
![]() $(y,z)$
with
$(y,z)$
with
![]() $y\in U$
and
$y\in U$
and
![]() $z\notin U$
such that modifying U by removing y and adding z (a ‘switch’) increases
$z\notin U$
such that modifying U by removing y and adding z (a ‘switch’) increases
![]() $e(G[U])$
by exactly
$e(G[U])$
by exactly
![]() $\ell $
. We define random variables that measure the number of ways to perform such switches and deduce Theorem 2.1 by studying certain moments of these random variables. Here, we again need to use some arguments involving ‘richness’ of Ramsey graphs, and we also make use of the technique of dependent random choice.
$\ell $
. We define random variables that measure the number of ways to perform such switches and deduce Theorem 2.1 by studying certain moments of these random variables. Here, we again need to use some arguments involving ‘richness’ of Ramsey graphs, and we also make use of the technique of dependent random choice.
3.6 Technical issues
The above subsections describe the high-level ideas of the proof, but there are various technical issues that arise, some of which have a substantial impact on the complexity of the proof. Most importantly, in the additively structured case, we outlined how to prove a conditional local limit theorem for the quadratic part Q, but we completely swept under the rug how to then ‘integrate’ this over outcomes of the conditioning. Explicitly, if we encode the bucket intersection sizes in a vector
![]() $\vec \Delta $
, we have outlined how to use Fourier-analytic techniques to prove certain estimates on conditional probabilities of the form
$\vec \Delta $
, we have outlined how to use Fourier-analytic techniques to prove certain estimates on conditional probabilities of the form
![]() $\Pr [|X-x|\le B|\vec \Delta ]$
, but we then need to average over the randomness of
$\Pr [|X-x|\le B|\vec \Delta ]$
, but we then need to average over the randomness of
![]() $\vec \Delta $
to obtain
$\vec \Delta $
to obtain
![]() $\Pr \left [|X-x|\le B\right ]=\mathbb E[\Pr [|X-x|\le B| \vec {\Delta }]]$
(taking into account that certain outcomes of
$\Pr \left [|X-x|\le B\right ]=\mathbb E[\Pr [|X-x|\le B| \vec {\Delta }]]$
(taking into account that certain outcomes of
![]() $\vec \Delta $
give a much larger contribution than others).
$\vec \Delta $
give a much larger contribution than others).
There are certain relatively simple arguments with which we can accomplish this averaging while losing logarithmic factors in the final probability bound (namely, using a concentration inequality for Q conditioned on
![]() $\vec {\Delta }$
, we can restrict to only a certain range of outcomes
$\vec {\Delta }$
, we can restrict to only a certain range of outcomes
![]() $\vec {\Delta }$
which give a significant contribution to the overall probability
$\vec {\Delta }$
which give a significant contribution to the overall probability
![]() $\Pr [|X-x|\le B]$
). To avoid logarithmic losses, we need to make sure that our conditional probability bounds ‘decay away from the mean’, which requires a nonuniform version of Theorem 1.6 (with a decay term), and some specialized tools for converting control of
$\Pr [|X-x|\le B]$
). To avoid logarithmic losses, we need to make sure that our conditional probability bounds ‘decay away from the mean’, which requires a nonuniform version of Theorem 1.6 (with a decay term), and some specialized tools for converting control of
![]() $|\varphi _{Y}(\tau )-\varphi _{Z}(\tau )|$
into bounds on small-ball probabilities for Y. Also, we need some delicate moment estimates comparing dependent random variables of ‘linear’ and ‘quadratic’ types to quantify the dependence between certain fluctuations in the conditional mean and variance as we vary
$|\varphi _{Y}(\tau )-\varphi _{Z}(\tau )|$
into bounds on small-ball probabilities for Y. Also, we need some delicate moment estimates comparing dependent random variables of ‘linear’ and ‘quadratic’ types to quantify the dependence between certain fluctuations in the conditional mean and variance as we vary
![]() $\vec \Delta $
.
$\vec \Delta $
.
Furthermore, for the switching argument described in the previous subsection, it is important (for technical reasons discussed in Remark 13.2) that in the setting of Theorem 3.1, B does not depend on A and H. To achieve this, we develop Fourier-analytic tools that take into account ‘local smoothness’ properties of the approximating random variable Z.
3.7 Organization of the paper
In Section 4, we collect a variety of (mostly known) tools which will be used throughout the paper. Then, in Section 5 we prove Theorem 1.6 (our sharp small-ball probability estimate for quadratic polynomials of Gaussians), and in Section 6 we prove some general ‘relative’ Esseen-type inequalities deducing bounds on small-ball probabilities from Fourier control.
In Sections 7 and 8, we obtain bounds on the characteristic function
![]() $\varphi _X(\tau )$
for various ranges of
$\varphi _X(\tau )$
for various ranges of
![]() $\tau $
(specifically, bounds due to ‘cancellation of the linear part’ appear in Section 7, and bounds due to ‘cancellation of the quadratic part’ appear in Section 8). This is already enough to handle the additively unstructured case of Theorem 3.1, which we do in Section 9.
$\tau $
(specifically, bounds due to ‘cancellation of the linear part’ appear in Section 7, and bounds due to ‘cancellation of the quadratic part’ appear in Section 8). This is already enough to handle the additively unstructured case of Theorem 3.1, which we do in Section 9.
Most of the rest of the paper is then devoted to the additively structured case of Theorem 3.1. In Section 10, we study the ‘robust rank’ of Ramsey graphs, and in Section 11 we prove some lemmas about quadratic polynomials on products of Boolean slices. All the ingredients collected so far come together in Section 12, where the additively structured case of Theorem 3.1 is proved.
Finally, in Section 13 we use a switching argument to deduce Theorem 2.1 from Theorem 3.1.
4 Preliminaries
In this section, we collect some basic definitions and tools that will be used throughout the paper.
4.1 Basic facts about Ramsey graphs
First, as mentioned in the introduction, the following classical result about Ramsey graphs is due to Erdős and Szemerédi [Reference Erdős and Szemerédi39].
Theorem 4.1. For any C, there exists
![]() $\varepsilon =\varepsilon (C)>0$
such that for every sufficiently large n, every C-Ramsey graph G on n vertices satisfies
$\varepsilon =\varepsilon (C)>0$
such that for every sufficiently large n, every C-Ramsey graph G on n vertices satisfies
![]() $\varepsilon \binom n 2\leq e(G)\leq (1-\varepsilon )\binom n 2$
.
$\varepsilon \binom n 2\leq e(G)\leq (1-\varepsilon )\binom n 2$
.
Remark 4.2. In the setting of Remark 1.3, where G has near-optimal spectral expansion, the expander mixing lemma (see, for example, [Reference Alon, Spencer, Wiley and Sons10, Corollary 9.2.5]) implies that (for sufficiently large n) all subsets of G with at least
![]() $n^{1/2+0.02}$
vertices have density very close to the overall density of G. It is possible to use this fact in lieu of Theorem 4.1 in our proof of Theorem 2.1.
$n^{1/2+0.02}$
vertices have density very close to the overall density of G. It is possible to use this fact in lieu of Theorem 4.1 in our proof of Theorem 2.1.
More recently, building on work of Bukh and Sudakov [Reference Bukh and Sudakov16], the first author and Sudakov [Reference Kwan and Sudakov67] proved that every Ramsey graph contains an induced subgraph in which the collection of vertex-neighborhoods is ‘rich’. Intuitively speaking, the richness condition here means that for all linear-size vertex subsets W, there are only very few vertex-neighborhoods that have an unusually large or unusually small intersection with W.
Definition 4.3. Consider
![]() $\delta ,\rho ,\alpha>0$
. We say that an m-vertex graph G is
$\delta ,\rho ,\alpha>0$
. We say that an m-vertex graph G is
![]() $(\delta ,\rho ,\alpha )$
-rich if for every subset
$(\delta ,\rho ,\alpha )$
-rich if for every subset
![]() $W\subseteq V(G)$
of size
$W\subseteq V(G)$
of size
![]() $|W|\geq \delta m$
, there are at most
$|W|\geq \delta m$
, there are at most
![]() $m^{\alpha }$
vertices
$m^{\alpha }$
vertices
![]() $v\in V(G)$
with the property that
$v\in V(G)$
with the property that
![]() $|N(v)\cap W|\leq \rho |W|$
or
$|N(v)\cap W|\leq \rho |W|$
or
![]() $|W\setminus N(v)|\leq \rho |W|$
.
$|W\setminus N(v)|\leq \rho |W|$
.
When the parameter
![]() $\alpha $
is omitted, it is assumed to take the value
$\alpha $
is omitted, it is assumed to take the value
![]() $1/5$
. That is to say, we write ‘
$1/5$
. That is to say, we write ‘
![]() $(\delta ,\rho )$
-rich’ to mean ‘
$(\delta ,\rho )$
-rich’ to mean ‘
![]() $(\delta ,\rho ,1/5)$
-rich’.
$(\delta ,\rho ,1/5)$
-rich’.
The following lemma is a slight generalization of [Reference Kwan and Sudakov67, Lemma 4] (and is proved in the same way).
Lemma 4.4. For any fixed
![]() $C,\alpha>0$
, there exists
$C,\alpha>0$
, there exists
![]() $\rho =\rho (C,\alpha )$
with
$\rho =\rho (C,\alpha )$
with
![]() $0<\rho <1$
such that the following holds. For n sufficiently large in terms of C and
$0<\rho <1$
such that the following holds. For n sufficiently large in terms of C and
![]() $\alpha $
, for any
$\alpha $
, for any
![]() $m\in \mathbb {R}$
with
$m\in \mathbb {R}$
with
![]() $\sqrt n\le m\leq \rho n$
, and any C-Ramsey graph G on n vertices, there is an induced subgraph of G on at least m vertices which is
$\sqrt n\le m\leq \rho n$
, and any C-Ramsey graph G on n vertices, there is an induced subgraph of G on at least m vertices which is
![]() $((m/n)^{\rho },\rho ,\alpha )$
-rich.
$((m/n)^{\rho },\rho ,\alpha )$
-rich.
For two disjoint vertex sets
![]() $U,W$
in a graph G, we write
$U,W$
in a graph G, we write
![]() $e(U,W)$
for the number of edges between
$e(U,W)$
for the number of edges between
![]() $U,W$
and write
$U,W$
and write
![]() $d(U,W)=e(U,W)/(|U||W|)$
for the density between
$d(U,W)=e(U,W)/(|U||W|)$
for the density between
![]() $U,W$
. We furthermore write
$U,W$
. We furthermore write
![]() $d(U)=e(U)/\binom {|U|}{2}$
for the density inside the set U.
$d(U)=e(U)/\binom {|U|}{2}$
for the density inside the set U.
Proof. We introduce an additional parameter K, which will be chosen to be large in terms of C and
![]() $\alpha $
. We will then choose
$\alpha $
. We will then choose
![]() $\rho =\rho (C,\alpha )$
with
$\rho =\rho (C,\alpha )$
with
![]() $0<\rho <1$
to be small in terms of K, C and
$0<\rho <1$
to be small in terms of K, C and
![]() $\alpha $
. We do not specify the values of K and
$\alpha $
. We do not specify the values of K and
![]() $\rho $
ahead of time but rather assume they are sufficiently large or small to satisfy certain inequalities that arise in the proof.
$\rho $
ahead of time but rather assume they are sufficiently large or small to satisfy certain inequalities that arise in the proof.
Let
![]() $\delta =(m/n)^{\rho }$
and suppose for the purpose of contradiction that every set of at least m vertices fails to induce a
$\delta =(m/n)^{\rho }$
and suppose for the purpose of contradiction that every set of at least m vertices fails to induce a
![]() $(\delta ,\rho ,\alpha )$
-rich subgraph. We will inductively construct a sequence of induced subgraphs
$(\delta ,\rho ,\alpha )$
-rich subgraph. We will inductively construct a sequence of induced subgraphs
![]() $G=G[U_{0}]\supseteq G[U_{1}]\supseteq \cdots \supseteq G[U_{K}]$
and disjoint vertex sets
$G=G[U_{0}]\supseteq G[U_{1}]\supseteq \cdots \supseteq G[U_{K}]$
and disjoint vertex sets
![]() $S_{1},\ldots ,S_{K}$
of size
$S_{1},\ldots ,S_{K}$
of size
![]() $|S_1|=\cdots =|S_K|=\lceil m^{\alpha }/2\rceil $
such that for each
$|S_1|=\cdots =|S_K|=\lceil m^{\alpha }/2\rceil $
such that for each
![]() $i=1,\ldots ,K$
, we have
$i=1,\ldots ,K$
, we have
![]() $|U_{i}|\ge (\delta /4)|U_{i-1}|$
and
$|U_{i}|\ge (\delta /4)|U_{i-1}|$
and
![]() $S_{i}\subseteq U_{i-1}\setminus U_i$
, as well as
$S_{i}\subseteq U_{i-1}\setminus U_i$
, as well as
This will suffice, as follows. First, note that for each
![]() $i=1,\ldots ,K$
, we have
$i=1,\ldots ,K$
, we have
 $$ \begin{align*}&\big[d(S_{i},S_{j})\leq 4\rho\text{ for all }j\in \{i+1,\ldots,K\}\big]\\ &\qquad \text{ or }\big[d(S_{i},S_{j})\geq 1-4\rho\text{ for all }j\in \{i+1,\ldots,K\}\big].\end{align*} $$
$$ \begin{align*}&\big[d(S_{i},S_{j})\leq 4\rho\text{ for all }j\in \{i+1,\ldots,K\}\big]\\ &\qquad \text{ or }\big[d(S_{i},S_{j})\geq 1-4\rho\text{ for all }j\in \{i+1,\ldots,K\}\big].\end{align*} $$
Without loss of generality suppose that the first case holds for at least half of the indices
![]() $i=1,\ldots ,K$
, and let S be the union of the corresponding sets
$i=1,\ldots ,K$
, and let S be the union of the corresponding sets
![]() $S_{i}$
. Then one can compute
$S_{i}$
. Then one can compute
![]() $d(S)\leq 4\rho +1/K$
. On the other hand,
$d(S)\leq 4\rho +1/K$
. On the other hand,
![]() $|S|\geq (K/2)\cdot m^{\alpha }/2\geq m^{\alpha }\geq n^{\alpha /2}$
and therefore
$|S|\geq (K/2)\cdot m^{\alpha }/2\geq m^{\alpha }\geq n^{\alpha /2}$
and therefore
![]() $G[S]$
is a
$G[S]$
is a
![]() $(2C/\alpha )$
-Ramsey graph. However, now the density bound
$(2C/\alpha )$
-Ramsey graph. However, now the density bound
![]() $d(S)\leq 4\rho +1/K$
contradicts Theorem 4.1 if
$d(S)\leq 4\rho +1/K$
contradicts Theorem 4.1 if
![]() $\rho $
is sufficiently small and K is sufficiently large (in terms of C and
$\rho $
is sufficiently small and K is sufficiently large (in terms of C and
![]() $\alpha $
).
$\alpha $
).
Let
![]() $U_{0}=V(G)$
. For
$U_{0}=V(G)$
. For
![]() $i=1,\ldots ,K$
we will construct the vertex sets
$i=1,\ldots ,K$
we will construct the vertex sets
![]() $U_{i}$
and
$U_{i}$
and
![]() $S_{i}$
, assuming that
$S_{i}$
, assuming that
![]() $U_{0},\ldots ,U_{i-1}$
and
$U_{0},\ldots ,U_{i-1}$
and
![]() $S_{1},\ldots ,S_{i-1}$
have already been constructed. Note that we have
$S_{1},\ldots ,S_{i-1}$
have already been constructed. Note that we have
![]() $|U_{i-1}|\ge (\delta /4)^{i-1}n\ge (\delta /4)^Kn=(m/n)^{\rho K}4^{-K}n\ge m$
, using that
$|U_{i-1}|\ge (\delta /4)^{i-1}n\ge (\delta /4)^Kn=(m/n)^{\rho K}4^{-K}n\ge m$
, using that
![]() $\rho K\leq 1/3$
and
$\rho K\leq 1/3$
and
![]() $m/n\leq \rho \leq 8^{-K}$
for
$m/n\leq \rho \leq 8^{-K}$
for
![]() $\rho $
being sufficiently small with respect to K. Therefore, by our assumption,
$\rho $
being sufficiently small with respect to K. Therefore, by our assumption,
![]() $U_{i-1}$
must contain a set W of at least
$U_{i-1}$
must contain a set W of at least
![]() $\delta |U_{i-1}|$
vertices and a set Y of more than
$\delta |U_{i-1}|$
vertices and a set Y of more than
![]() $|U_{i-1}|^{\alpha }\geq m^{\alpha }$
vertices contradicting
$|U_{i-1}|^{\alpha }\geq m^{\alpha }$
vertices contradicting
![]() $(\delta ,\rho ,\alpha )$
-richness. Suppose without loss of generality that
$(\delta ,\rho ,\alpha )$
-richness. Suppose without loss of generality that
![]() $|N(v)\cap W|\le \rho |W|$
for at least half of the vertices
$|N(v)\cap W|\le \rho |W|$
for at least half of the vertices
![]() $v\in Y$
, and let
$v\in Y$
, and let
![]() $S_{i}\subseteq Y\subseteq U_{i-1}$
be a set of precisely
$S_{i}\subseteq Y\subseteq U_{i-1}$
be a set of precisely
![]() $\lceil m^{\alpha }/2\rceil $
such vertices
$\lceil m^{\alpha }/2\rceil $
such vertices
![]() $v\in Y$
. Then, let
$v\in Y$
. Then, let
![]() $U=W\setminus S_{i}\subseteq U_{i-1}\setminus S_i$
, and note that we have
$U=W\setminus S_{i}\subseteq U_{i-1}\setminus S_i$
, and note that we have
![]() $|U|\ge |W|/2$
since
$|U|\ge |W|/2$
since
![]() $|W|\geq \delta |U_{i-1}|\geq 4 \cdot (\delta /4)^Kn\geq 4m\geq 2|S_{i}|$
. Furthermore, let
$|W|\geq \delta |U_{i-1}|\geq 4 \cdot (\delta /4)^Kn\geq 4m\geq 2|S_{i}|$
. Furthermore, let
![]() $U_{i}\subseteq U$
be the set of vertices
$U_{i}\subseteq U$
be the set of vertices
![]() $u\in U$
with
$u\in U$
with
![]() $e(S_{i}, \{ u\} )\le 4\rho \cdot |S_i|$
. Now, we just need to show
$e(S_{i}, \{ u\} )\le 4\rho \cdot |S_i|$
. Now, we just need to show
![]() $|U_{i}|\ge (\delta /4)|U_{i-1}|$
. To this end, note that for all
$|U_{i}|\ge (\delta /4)|U_{i-1}|$
. To this end, note that for all
![]() $v\in S_{i}$
we have
$v\in S_{i}$
we have
![]() $e(\{ v\} ,U)=|N(v)\cap U|\le |N(v)\cap W|\leq \rho |W|\leq 2\rho |U|$
. Hence,
$e(\{ v\} ,U)=|N(v)\cap U|\le |N(v)\cap W|\leq \rho |W|\leq 2\rho |U|$
. Hence,
 $$ \begin{align*} |U\setminus U_{i}|\cdot 4\rho\cdot |S_i|&\leq \sum_{w\in U\setminus U_{i}}e(S_{i},\{ w\})=e(S_{i},U\setminus U_{i} )\\ &\le e(S_{i},U)=\sum_{v\in S_{i}}e(\{ v\} ,U)\le |S_i|\cdot 2\rho|U|, \end{align*} $$
$$ \begin{align*} |U\setminus U_{i}|\cdot 4\rho\cdot |S_i|&\leq \sum_{w\in U\setminus U_{i}}e(S_{i},\{ w\})=e(S_{i},U\setminus U_{i} )\\ &\le e(S_{i},U)=\sum_{v\in S_{i}}e(\{ v\} ,U)\le |S_i|\cdot 2\rho|U|, \end{align*} $$
implying that
![]() $|U\setminus U_i|\leq |U|/2$
and hence
$|U\setminus U_i|\leq |U|/2$
and hence
![]() $|U_{i}|\geq |U|/2\ge |W|/4\geq (\delta /4)|U_{i-1}|$
, as desired.
$|U_{i}|\geq |U|/2\ge |W|/4\geq (\delta /4)|U_{i-1}|$
, as desired.
Remark 4.5. In the setting of Remark 1.3, where G is dense and has near-optimal spectral expansion (and n is sufficiently large), the expander mixing lemma can be used to prove that every induced subgraph of G on at least
![]() $n^{0.9}$
vertices is
$n^{0.9}$
vertices is
![]() $(n^{-0.05},0.005,\alpha )$
-rich (and therefore Lemma 4.4 holds) for
$(n^{-0.05},0.005,\alpha )$
-rich (and therefore Lemma 4.4 holds) for
![]() $\alpha \ge 0.2$
. It is possible to use this in lieu of Lemma 4.4 in our proof of Theorem 2.1.
$\alpha \ge 0.2$
. It is possible to use this in lieu of Lemma 4.4 in our proof of Theorem 2.1.
4.2 Characteristic functions and anticoncentration
For a real random variable X, recall that the characteristic function
![]() $\varphi _X\colon \mathbb {R}\to \mathbb C$
is defined by
$\varphi _X\colon \mathbb {R}\to \mathbb C$
is defined by
![]() $\varphi _X(t)=\mathbb E [e^{itX}]$
. Note that we have
$\varphi _X(t)=\mathbb E [e^{itX}]$
. Note that we have
![]() $|\varphi _X(t)|\le 1$
for all
$|\varphi _X(t)|\le 1$
for all
![]() $t\in \mathbb {R}$
. If
$t\in \mathbb {R}$
. If
![]() $\varphi _X(t)$
is absolutely integrable, then X has a continuous density
$\varphi _X(t)$
is absolutely integrable, then X has a continuous density
![]() $p_X$
, which can be obtained by the inversion formula
$p_X$
, which can be obtained by the inversion formula
Next, recall the Lévy concentration function, which measures the maximum small-ball probability.
Definition 4.6. For a real random variable X and
![]() $\varepsilon \ge 0$
, we define
$\varepsilon \ge 0$
, we define
![]() $\mathcal {L}(X,\varepsilon ) = \sup _{x\in \mathbb {R}}\Pr [|X-x|\le \varepsilon ]$
.
$\mathcal {L}(X,\varepsilon ) = \sup _{x\in \mathbb {R}}\Pr [|X-x|\le \varepsilon ]$
.
If X has a density
![]() $p_X$
, then we trivially have
$p_X$
, then we trivially have
![]() $\mathcal {L}(X,\varepsilon )\le \varepsilon \max _{x\in \mathbb {R}} p_X(x)$
. We can also control small-ball probabilities using only a certain range of values of the characteristic function, via Esseen’s inequality (see, for example, [Reference Rudelson86, Lemma 6.4]):
$\mathcal {L}(X,\varepsilon )\le \varepsilon \max _{x\in \mathbb {R}} p_X(x)$
. We can also control small-ball probabilities using only a certain range of values of the characteristic function, via Esseen’s inequality (see, for example, [Reference Rudelson86, Lemma 6.4]):
Theorem 4.7. There is
![]() $C_{4.7}> 0$
so that for any real random variable X and any
$C_{4.7}> 0$
so that for any real random variable X and any
![]() $\varepsilon> 0$
, we have
$\varepsilon> 0$
, we have
 $$\begin{align*}\mathcal L(X,\varepsilon)\le C_{4.7}\cdot \varepsilon \int_{-2/\varepsilon}^{2/\varepsilon}|\varphi_X(t)|\,dt. \end{align*}$$
$$\begin{align*}\mathcal L(X,\varepsilon)\le C_{4.7}\cdot \varepsilon \int_{-2/\varepsilon}^{2/\varepsilon}|\varphi_X(t)|\,dt. \end{align*}$$
In Section 6 we will prove some more sophisticated ‘relative’ variants of Theorem 4.7.
4.3 Distance-to-integer estimates and regularized least common denominator
For
![]() $r\in \mathbb {R}$
, let
$r\in \mathbb {R}$
, let
![]() $\|r\|_{\mathbb {R}/\mathbb Z}$
denote the (Euclidean) distance of r to the nearest integer. Recall that the Rademacher distribution is the uniform distribution on the set
$\|r\|_{\mathbb {R}/\mathbb Z}$
denote the (Euclidean) distance of r to the nearest integer. Recall that the Rademacher distribution is the uniform distribution on the set
![]() $\{-1,1\}$
. If x is Rademacher distributed, then for any
$\{-1,1\}$
. If x is Rademacher distributed, then for any
![]() $r\in \mathbb {R}$
we have the well-known estimate
$r\in \mathbb {R}$
we have the well-known estimate
If
![]() $\vec \xi \in \{0,1\}^n$
is a uniformly random length-n binary vector, then for any
$\vec \xi \in \{0,1\}^n$
is a uniformly random length-n binary vector, then for any
![]() $\vec a\in \mathbb {R}^n$
and any
$\vec a\in \mathbb {R}^n$
and any
![]() $b\in \mathbb {R}$
, we can rewrite
$b\in \mathbb {R}$
, we can rewrite
![]() $\vec a\cdot \vec \xi +b$
as a weighted sum of independent Rademacher random variables. Specifically, we have
$\vec a\cdot \vec \xi +b$
as a weighted sum of independent Rademacher random variables. Specifically, we have
![]() $\vec a\cdot \vec \xi +b=\vec {r}\cdot \vec {x}+\mathbb E [\vec a\cdot \vec \xi +b]$
, where
$\vec a\cdot \vec \xi +b=\vec {r}\cdot \vec {x}+\mathbb E [\vec a\cdot \vec \xi +b]$
, where
![]() $\vec {r}=\vec {a}/2 \in \mathbb {R}^n$
and
$\vec {r}=\vec {a}/2 \in \mathbb {R}^n$
and
![]() $\vec {x}\in \{-1,1\}^n$
is obtained from
$\vec {x}\in \{-1,1\}^n$
is obtained from
![]() $\vec \xi \in \{0,1\}^n$
by replacing all zeroes by
$\vec \xi \in \{0,1\}^n$
by replacing all zeroes by
![]() $-1$
’s. Then
$-1$
’s. Then
![]() $\vec {x}$
is uniformly random in
$\vec {x}$
is uniformly random in
![]() $\{-1,1\}^n$
, so (4.2) yields
$\{-1,1\}^n$
, so (4.2) yields
 $$ \begin{align} \mathbb{E}[\exp(i(\vec{a}\cdot\vec{\xi}+b))]|=|\mathbb{E}[\exp(i(\vec{r}\cdot \vec{x}))]|&=\prod_{j=1}^{n} |\mathbb{E}[\exp(ir_jx_j)]|\notag \\ &\leq \exp\Bigg(-\sum_{j=1}^{n}\lVert a_j/(2\pi)\rVert_{\mathbb{R}/\mathbb{Z}}^2\Bigg). \end{align} $$
$$ \begin{align} \mathbb{E}[\exp(i(\vec{a}\cdot\vec{\xi}+b))]|=|\mathbb{E}[\exp(i(\vec{r}\cdot \vec{x}))]|&=\prod_{j=1}^{n} |\mathbb{E}[\exp(ir_jx_j)]|\notag \\ &\leq \exp\Bigg(-\sum_{j=1}^{n}\lVert a_j/(2\pi)\rVert_{\mathbb{R}/\mathbb{Z}}^2\Bigg). \end{align} $$
In the case where we want to study
![]() $\vec a\cdot \vec x$
where
$\vec a\cdot \vec x$
where
![]() $\vec x\in \{0,1\}^n$
is a uniformly random binary vector with a given number of ones (i.e., a random vector on a Boolean slice), one has the following estimate.
$\vec x\in \{0,1\}^n$
is a uniformly random binary vector with a given number of ones (i.e., a random vector on a Boolean slice), one has the following estimate.
Lemma 4.8. Fix
![]() $c>0$
. Let
$c>0$
. Let
![]() $\vec {a}\in \mathbb {R}^{n}$
, and suppose that for some
$\vec {a}\in \mathbb {R}^{n}$
, and suppose that for some
![]() $0< \delta \le 1/2$
there are disjoint pairs
$0< \delta \le 1/2$
there are disjoint pairs
![]() $\{i_{1},j_{1}\},\ldots ,\{i_{M},j_{M}\}\subseteq [n]$
such that
$\{i_{1},j_{1}\},\ldots ,\{i_{M},j_{M}\}\subseteq [n]$
such that
![]() $\|(a_{i_{k}}-a_{j_{k}})/(2\pi )\|_{\mathbb {R}/\mathbb Z}\ge \delta $
for each
$\|(a_{i_{k}}-a_{j_{k}})/(2\pi )\|_{\mathbb {R}/\mathbb Z}\ge \delta $
for each
![]() $k=1,\ldots ,M$
. Let s be an integer with
$k=1,\ldots ,M$
. Let s be an integer with
![]() $cn\le s\le (1-c)n$
. Then for a random zero-one vector
$cn\le s\le (1-c)n$
. Then for a random zero-one vector
![]() $\vec {\xi }\in \left \{ 0,1\right \}^{n}$
with exactly s ones, we have
$\vec {\xi }\in \left \{ 0,1\right \}^{n}$
with exactly s ones, we have
Lemma 4.8 can be deduced from [Reference Roos85, Theorem 1.1]. For the reader’s convenience, we include an alternative proof, reducing it to (4.3).
Proof. We may assume that
![]() $M\leq cn/4$
(indeed, noting that
$M\leq cn/4$
(indeed, noting that
![]() $M\leq n/2$
we can otherwise just replace M by
$M\leq n/2$
we can otherwise just replace M by
![]() $\lfloor cn/4\rfloor $
). The random vector
$\lfloor cn/4\rfloor $
). The random vector
![]() $\vec {\xi }$
corresponds to a uniformly random subset
$\vec {\xi }$
corresponds to a uniformly random subset
![]() $U\subseteq [n]$
of size s. Let us first expose the intersection sizes
$U\subseteq [n]$
of size s. Let us first expose the intersection sizes
![]() $|U\cap \{i_1,j_1\}|, \ldots , |U\cap \{i_M,j_M\}|$
, one at a time. For each
$|U\cap \{i_1,j_1\}|, \ldots , |U\cap \{i_M,j_M\}|$
, one at a time. For each
![]() $k=1,\ldots ,M$
, we have
$k=1,\ldots ,M$
, we have
![]() $|U\cap \{i_k,j_k\}|=1$
with probability at least
$|U\cap \{i_k,j_k\}|=1$
with probability at least
![]() $c(1-c)/4$
even when conditioning on any outcomes for the previously exposed intersection sizes
$c(1-c)/4$
even when conditioning on any outcomes for the previously exposed intersection sizes
![]() $|U\cap \{i_1,j_1\}|, \ldots , |U\cap \{i_{k-1},j_{k-1}\}|$
. Hence, the number of indices
$|U\cap \{i_1,j_1\}|, \ldots , |U\cap \{i_{k-1},j_{k-1}\}|$
. Hence, the number of indices
![]() $k\in [M]$
with
$k\in [M]$
with
![]() $|U\cap \{i_k,j_k\}|=1$
stochastically dominates a binomial random variable with distribution
$|U\cap \{i_k,j_k\}|=1$
stochastically dominates a binomial random variable with distribution
![]() $\mathrm {Bin}(M,c(1-c)/4)$
. Thus, by a Chernoff bound (see, e.g., Lemma 4.16), with probability at least
$\mathrm {Bin}(M,c(1-c)/4)$
. Thus, by a Chernoff bound (see, e.g., Lemma 4.16), with probability at least
![]() $1-\exp (-\Omega _c(M))$
there is a set
$1-\exp (-\Omega _c(M))$
there is a set
![]() $K\subseteq [M]$
of at least
$K\subseteq [M]$
of at least
![]() $c(1-c)M/8$
indices k with
$c(1-c)M/8$
indices k with
![]() $|U\cap \{i_k,j_k\}|=1$
. Let us expose and condition on all coordinates of
$|U\cap \{i_k,j_k\}|=1$
. Let us expose and condition on all coordinates of
![]() $\vec {\xi }\in \{0,1\}^n$
except those in
$\vec {\xi }\in \{0,1\}^n$
except those in
![]() $\bigcup _{k\in K}\{i_k,j_k\}$
. The only remaining randomness of the vector
$\bigcup _{k\in K}\{i_k,j_k\}$
. The only remaining randomness of the vector
![]() $\vec {\xi }\in \{0,1\}^n$
is that for each
$\vec {\xi }\in \{0,1\}^n$
is that for each
![]() $k\in K$
we have either
$k\in K$
we have either
![]() $\xi _{i_k}=1$
or
$\xi _{i_k}=1$
or
![]() $\xi _{j_k}=1$
(each with probability
$\xi _{j_k}=1$
(each with probability
![]() $1/2$
, independently for all
$1/2$
, independently for all
![]() $k\in K$
). Thus, after all of this conditioning, we have
$k\in K$
). Thus, after all of this conditioning, we have
![]() $\vec {a}\cdot \vec {\xi }=\sum _{k\in K} (a_{i_k}-a_{j_k})\xi _{i_k}+b$
for some
$\vec {a}\cdot \vec {\xi }=\sum _{k\in K} (a_{i_k}-a_{j_k})\xi _{i_k}+b$
for some
![]() $b\in \mathbb {R}$
, where
$b\in \mathbb {R}$
, where
![]() $(\xi _{i_k})_{k\in K}\in \{0,1\}^K$
is uniformly random. Thus, (4.3) implies
$(\xi _{i_k})_{k\in K}\in \{0,1\}^K$
is uniformly random. Thus, (4.3) implies
![]() $|\mathbb E[\exp (i(\vec {a}\cdot \vec {\xi }))]|\leq \exp (-\sum _{k\in K} \|(a_{i_{k}}-a_{j_{k}})/(2\pi )\|_{\mathbb {R}/\mathbb Z}^2)\leq \exp (-\Omega _c(M\delta ^2))$
, as desired.
$|\mathbb E[\exp (i(\vec {a}\cdot \vec {\xi }))]|\leq \exp (-\sum _{k\in K} \|(a_{i_{k}}-a_{j_{k}})/(2\pi )\|_{\mathbb {R}/\mathbb Z}^2)\leq \exp (-\Omega _c(M\delta ^2))$
, as desired.
The above estimates motivate the notion of the essential least common denominator (LCD) of a vector
![]() $\vec v \in \mathbb {S}^{n-1}\subseteq \mathbb {R}^n$
(where
$\vec v \in \mathbb {S}^{n-1}\subseteq \mathbb {R}^n$
(where
![]() $\mathbb {S}^{n-1}$
is the unit sphere in
$\mathbb {S}^{n-1}$
is the unit sphere in
![]() $\mathbb {R}^n$
). The following formulation of this notion was proposed by Rudelson (see [Reference Vershynin95, (1.17)] and the remarks preceding), in the context of random matrix theory.
$\mathbb {R}^n$
). The following formulation of this notion was proposed by Rudelson (see [Reference Vershynin95, (1.17)] and the remarks preceding), in the context of random matrix theory.
Definition 4.9 (LCD)
For
![]() $t>0$
, let
$t>0$
, let
![]() $\log _+t = \max \{0,\log t\}$
. For
$\log _+t = \max \{0,\log t\}$
. For
![]() $L\ge 1$
and
$L\ge 1$
and
![]() $\vec v \in \mathbb {S}^{n-1}\subseteq \mathbb {R}^n$
, the (essential) least common denominatorFootnote 7
$\vec v \in \mathbb {S}^{n-1}\subseteq \mathbb {R}^n$
, the (essential) least common denominatorFootnote 7
![]() $D_L(\vec v)$
is defined as
$D_L(\vec v)$
is defined as
(Here
![]() $\operatorname {dist}(\theta \vec v, \mathbb {Z}^{n})=\sqrt {\sum _{i=1}^n \|\theta v_i\|_{\mathbb {R}/\mathbb Z}^2}$
denotes the Euclidean distance from
$\operatorname {dist}(\theta \vec v, \mathbb {Z}^{n})=\sqrt {\sum _{i=1}^n \|\theta v_i\|_{\mathbb {R}/\mathbb Z}^2}$
denotes the Euclidean distance from
![]() $\theta \vec v$
to the nearest point in the integer lattice
$\theta \vec v$
to the nearest point in the integer lattice
![]() $\mathbb Z^n$
.)
$\mathbb Z^n$
.)
The following lemma gives a lower bound on the LCD of a unit vector
![]() $\vec v$
in terms of
$\vec v$
in terms of
![]() $\lVert \vec v\rVert _{\infty }$
.
$\lVert \vec v\rVert _{\infty }$
.
Lemma 4.10 [Reference Vershynin95, Lemma 6.2]
If
![]() $\vec v\in \mathbb {S}^{n-1}$
and
$\vec v\in \mathbb {S}^{n-1}$
and
![]() $L\ge 1$
, then
$L\ge 1$
, then
Proof. Note that for
![]() $\theta \le 1/(2\lVert \vec v\rVert _{\infty })$
we have that
$\theta \le 1/(2\lVert \vec v\rVert _{\infty })$
we have that
![]() $\lVert \theta \vec {v}\rVert _{\infty }\le 1/2$
. Thus, we have that
$\lVert \theta \vec {v}\rVert _{\infty }\le 1/2$
. Thus, we have that
where we have used that
![]() $x>\sqrt {\log _{+}(x)}$
for
$x>\sqrt {\log _{+}(x)}$
for
![]() $x> 0$
. The result follows by the definition of LCD.
$x> 0$
. The result follows by the definition of LCD.
If
![]() $D_L(\vec v)$
is large, then we can obtain strong control over the characteristic function of random variables of the form
$D_L(\vec v)$
is large, then we can obtain strong control over the characteristic function of random variables of the form
![]() $\vec v\cdot \vec x$
, for an i.i.d. Rademacher vector
$\vec v\cdot \vec x$
, for an i.i.d. Rademacher vector
![]() $\vec x$
(specifically, we are able to compare such characteristic functions to the characteristic function
$\vec x$
(specifically, we are able to compare such characteristic functions to the characteristic function
![]() $\varphi _Z(t)=e^{-t^2/2}$
of a standard Gaussian
$\varphi _Z(t)=e^{-t^2/2}$
of a standard Gaussian
![]() $Z\sim \mathcal N(0,1)$
). However, if
$Z\sim \mathcal N(0,1)$
). However, if
![]() $D_L(\vec v)$
is small, then in a certain sense
$D_L(\vec v)$
is small, then in a certain sense
![]() $\vec v$
is ‘additively structured’, and we can deduce certain combinatorial consequences. Actually, to obtain the consequences we need, we will use the following more robust notion known as regularized LCD, introduced by Vershynin [Reference Vershynin95].
$\vec v$
is ‘additively structured’, and we can deduce certain combinatorial consequences. Actually, to obtain the consequences we need, we will use the following more robust notion known as regularized LCD, introduced by Vershynin [Reference Vershynin95].
Definition 4.11 (regularized LCD)
Fix
![]() $L\ge 1$
and
$L\ge 1$
and
![]() $0<\gamma <1$
. For a vector
$0<\gamma <1$
. For a vector
![]() $\vec v\in \mathbb {R}^n$
with fewer than
$\vec v\in \mathbb {R}^n$
with fewer than
![]() $n^{1-\gamma }$
zero coordinates, the regularized least common denominator (RLCD)
$n^{1-\gamma }$
zero coordinates, the regularized least common denominator (RLCD)
![]() $\widehat {D}_{L,\gamma }(\vec v)$
, is defined as
$\widehat {D}_{L,\gamma }(\vec v)$
, is defined as
where
![]() $\vec {v}_I\in \mathbb {R}^I$
denotes the restriction of
$\vec {v}_I\in \mathbb {R}^I$
denotes the restriction of
![]() $\vec v$
to the indices in I.
$\vec v$
to the indices in I.
If a vector
![]() $\vec {d}$
is ‘additively structured’ in the sense of having small RLCD, we can partition its index set into a small number of ‘buckets’ such that the values of
$\vec {d}$
is ‘additively structured’ in the sense of having small RLCD, we can partition its index set into a small number of ‘buckets’ such that the values of
![]() $d_i$
are similar inside each bucket. This is closely related to
$d_i$
are similar inside each bucket. This is closely related to
![]() $\varepsilon $
-net arguments using LCD assumptions that have previously appeared in the random matrix theory literature (see, for example, [Reference Rudelson86, Lemma 7.2]).
$\varepsilon $
-net arguments using LCD assumptions that have previously appeared in the random matrix theory literature (see, for example, [Reference Rudelson86, Lemma 7.2]).
Lemma 4.12. Fix
![]() $H> 0$
and
$H> 0$
and
![]() $0<\gamma <1/4$
and
$0<\gamma <1/4$
and
![]() $L\ge 1$
. Let
$L\ge 1$
. Let
![]() $\vec {d}\in \mathbb {R}_{\ge 0}^{n}$
be a vector such that
$\vec {d}\in \mathbb {R}_{\ge 0}^{n}$
be a vector such that
![]() $\lVert \vec {d}\rVert _{\infty }\le Hn$
and
$\lVert \vec {d}\rVert _{\infty }\le Hn$
and
![]() $\lVert \vec {d}_S\rVert _2\geq n^{3/2-2\gamma }$
for every subset
$\lVert \vec {d}_S\rVert _2\geq n^{3/2-2\gamma }$
for every subset
![]() $S\subseteq [n]$
of size
$S\subseteq [n]$
of size
![]() $|S|=\lceil n^{1-\gamma }\rceil $
, and assume that n is sufficiently large with respect to H,
$|S|=\lceil n^{1-\gamma }\rceil $
, and assume that n is sufficiently large with respect to H,
![]() $\gamma $
and L.
$\gamma $
and L.
If
![]() $\widehat {D}_{L,\gamma }(\vec {d}) \le n^{1/2}$
, then there exists a partition
$\widehat {D}_{L,\gamma }(\vec {d}) \le n^{1/2}$
, then there exists a partition
![]() $[n] = R\cup (I_1\cup \cdots \cup I_m)$
and real numbers
$[n] = R\cup (I_1\cup \cdots \cup I_m)$
and real numbers
![]() $\kappa _1,\ldots ,\kappa _m\ge 0$
with
$\kappa _1,\ldots ,\kappa _m\ge 0$
with
![]() $|R|\le n^{1-\gamma }$
and
$|R|\le n^{1-\gamma }$
and
![]() $|I_1|=\cdots =|I_m|=\lceil n^{1-2\gamma }\rceil $
such that for all
$|I_1|=\cdots =|I_m|=\lceil n^{1-2\gamma }\rceil $
such that for all
![]() $j=1,\ldots ,m$
and
$j=1,\ldots ,m$
and
![]() $i\in I_j$
we have
$i\in I_j$
we have
![]() $|d_i - \kappa _j|\le n^{1/2+4\gamma }$
.
$|d_i - \kappa _j|\le n^{1/2+4\gamma }$
.
Proof. Choose a partition
![]() $[n] = R\cup (I_1\cup \cdots \cup I_m)$
and
$[n] = R\cup (I_1\cup \cdots \cup I_m)$
and
![]() $\kappa _j\geq 0$
for
$\kappa _j\geq 0$
for
![]() $j=1,\ldots ,m$
with
$j=1,\ldots ,m$
with
![]() $|I_1|=\cdots =|I_m| = \lceil n^{1-2\gamma }\rceil $
such that
$|I_1|=\cdots =|I_m| = \lceil n^{1-2\gamma }\rceil $
such that
![]() $|d_i-\kappa _j|\le n^{1/2+4\gamma }$
for all
$|d_i-\kappa _j|\le n^{1/2+4\gamma }$
for all
![]() $1\le j\le m$
and
$1\le j\le m$
and
![]() $i\in I_j$
, such that m is as large as possible. It then suffices to prove that
$i\in I_j$
, such that m is as large as possible. It then suffices to prove that
![]() $|R|\leq n^{1-\gamma }$
.
$|R|\leq n^{1-\gamma }$
.
So let us assume for contradiction that
![]() $|R|>n^{1-\gamma }$
, and fix a subset
$|R|>n^{1-\gamma }$
, and fix a subset
![]() $S\subseteq R$
of size
$S\subseteq R$
of size
![]() $|S|=\lceil n^{1-\gamma }\rceil $
. Note that
$|S|=\lceil n^{1-\gamma }\rceil $
. Note that
![]() $D_L(\vec {d}_S/\lVert \vec {d}_S\rVert _2)\le \widehat {D}_{L,\gamma }(\vec {d})\le n^{1/2}$
by Definition 4.11. Furthermore, since
$D_L(\vec {d}_S/\lVert \vec {d}_S\rVert _2)\le \widehat {D}_{L,\gamma }(\vec {d})\le n^{1/2}$
by Definition 4.11. Furthermore, since
![]() $\lVert \vec {d}_S/\lVert \vec {d}_S\rVert _2\rVert _{\infty }\le Hn/n^{3/2-2\gamma }= Hn^{-1/2+2\gamma }$
, Lemma 4.10 implies
$\lVert \vec {d}_S/\lVert \vec {d}_S\rVert _2\rVert _{\infty }\le Hn/n^{3/2-2\gamma }= Hn^{-1/2+2\gamma }$
, Lemma 4.10 implies
![]() $D_L(\vec {d}_S/\lVert \vec {d}_S\rVert _2)\ge (H^{-1}/2) n^{1/2-2\gamma }$
. Thus, by Definition 4.9, there is some
$D_L(\vec {d}_S/\lVert \vec {d}_S\rVert _2)\ge (H^{-1}/2) n^{1/2-2\gamma }$
. Thus, by Definition 4.9, there is some
![]() $\theta \in [(H^{-1}/2)n^{1/2-2\gamma },2n^{1/2}]$
such that
$\theta \in [(H^{-1}/2)n^{1/2-2\gamma },2n^{1/2}]$
such that
for some
![]() $\vec {w}\in \mathbb {Z}^{S}$
. By choosing
$\vec {w}\in \mathbb {Z}^{S}$
. By choosing
![]() $\vec {w}$
to minimize the left-hand side, we may assume that
$\vec {w}$
to minimize the left-hand side, we may assume that
![]() $\vec {w}$
has nonnegative entries (recall that
$\vec {w}$
has nonnegative entries (recall that
![]() $\vec {d}$
has nonnegative entries).
$\vec {d}$
has nonnegative entries).
Now, the number of indices
![]() $i\in S$
with
$i\in S$
with
![]() $|(\theta /\lVert \vec {d}_S\rVert _2)d_i-w_i|> n^{-1/2+2\gamma }$
is at most
$|(\theta /\lVert \vec {d}_S\rVert _2)d_i-w_i|> n^{-1/2+2\gamma }$
is at most
 $$\begin{align*}\frac{\lVert(\theta/\lVert\vec{d}_S\rVert_2)\vec{d}_S-\vec{w}\rVert_2^2}{n^{-1+4\gamma}}\leq \frac{L^2 \log n}{n^{-1+4\gamma}}\le n^{1-3\gamma}.\end{align*}$$
$$\begin{align*}\frac{\lVert(\theta/\lVert\vec{d}_S\rVert_2)\vec{d}_S-\vec{w}\rVert_2^2}{n^{-1+4\gamma}}\leq \frac{L^2 \log n}{n^{-1+4\gamma}}\le n^{1-3\gamma}.\end{align*}$$
Furthermore, note that
![]() $\theta \leq 2n^{1/2}$
and (4.4) imply
$\theta \leq 2n^{1/2}$
and (4.4) imply
![]() $\lVert \vec {w}\rVert _2\le 3n^{1/2}$
, and hence, the number of indices
$\lVert \vec {w}\rVert _2\le 3n^{1/2}$
, and hence, the number of indices
![]() $i\in S$
with
$i\in S$
with
![]() $w_i\geq n^{2\gamma /3}$
is at most
$w_i\geq n^{2\gamma /3}$
is at most
![]() $9n^{1-4\gamma /3}$
. Thus, as
$9n^{1-4\gamma /3}$
. Thus, as
![]() $|S|=\lceil n^{1-\gamma }\rceil $
, there must be at least
$|S|=\lceil n^{1-\gamma }\rceil $
, there must be at least
![]() $|S|/2\geq n^{1-\gamma }/2$
indices
$|S|/2\geq n^{1-\gamma }/2$
indices
![]() $i\in S$
with
$i\in S$
with
![]() $|(\theta /\lVert \vec {d}_S\rVert _2)d_i-w_i|\leq n^{-1/2+2\gamma }$
and
$|(\theta /\lVert \vec {d}_S\rVert _2)d_i-w_i|\leq n^{-1/2+2\gamma }$
and
![]() $w_i\in [0,n^{2\gamma /3}]\cap \mathbb {Z}$
. Hence, by the pigeonhole principle there is some
$w_i\in [0,n^{2\gamma /3}]\cap \mathbb {Z}$
. Hence, by the pigeonhole principle there is some
![]() $\kappa \geq 0$
and a subset
$\kappa \geq 0$
and a subset
![]() $I_{m+1}\subseteq S\subseteq R$
of size
$I_{m+1}\subseteq S\subseteq R$
of size
![]() $|I_{m+1}| = \lceil n^{1-2\gamma }\rceil $
such that for all
$|I_{m+1}| = \lceil n^{1-2\gamma }\rceil $
such that for all
![]() $i\in I_{m+1}$
we have
$i\in I_{m+1}$
we have
![]() $w_i=\kappa $
and
$w_i=\kappa $
and
 $$ \begin{align*}|(\theta/\lVert\vec{d}_S\rVert_2)d_i-\kappa |=|(\theta/\lVert\vec{d}_S\rVert_2)d_i-w_i|&\leq n^{-1/2+2\gamma}= \frac{n^{1/2-2\gamma}}{n^{(1-\gamma)/2}n}\cdot n^{1/2+(7/2)\gamma}\\ &\lesssim_H \frac{\theta}{\lVert\vec{d}_S\rVert_2}\cdot n^{1/2+(7/2)\gamma}. \end{align*} $$
$$ \begin{align*}|(\theta/\lVert\vec{d}_S\rVert_2)d_i-\kappa |=|(\theta/\lVert\vec{d}_S\rVert_2)d_i-w_i|&\leq n^{-1/2+2\gamma}= \frac{n^{1/2-2\gamma}}{n^{(1-\gamma)/2}n}\cdot n^{1/2+(7/2)\gamma}\\ &\lesssim_H \frac{\theta}{\lVert\vec{d}_S\rVert_2}\cdot n^{1/2+(7/2)\gamma}. \end{align*} $$
Defining
![]() $\kappa _{m+1}=(\lVert \vec {d}_S\rVert _2/\theta )\kappa \geq 0$
, this implies
$\kappa _{m+1}=(\lVert \vec {d}_S\rVert _2/\theta )\kappa \geq 0$
, this implies
![]() $|d_i-\kappa _{m+1}|\leq n^{1/2+4\gamma }$
for all
$|d_i-\kappa _{m+1}|\leq n^{1/2+4\gamma }$
for all
![]() $i\in I_{m+1}$
. But now the partition
$i\in I_{m+1}$
. But now the partition
![]() $V(G) = (R\setminus I_{m+1})\cup (I_1\cup \cdots \cup I_{m+1})$
contradicts the maximality of m.
$V(G) = (R\setminus I_{m+1})\cup (I_1\cup \cdots \cup I_{m+1})$
contradicts the maximality of m.
4.4 Low-rank approximation
Recall the definition of the Frobenius norm (also called the Hilbert–Schmidt norm): For a matrix
![]() $M\in \mathbb {R}^{n\times n}$
, we have
$M\in \mathbb {R}^{n\times n}$
, we have
 $$\begin{align*}\|M\|_{\mathrm{F}}=\Big(\sum_{i,j=1}^n M_{ij}^2\Big)^{1/2}=\sqrt{\operatorname{trace}(M^\intercal M)}.\end{align*}$$
$$\begin{align*}\|M\|_{\mathrm{F}}=\Big(\sum_{i,j=1}^n M_{ij}^2\Big)^{1/2}=\sqrt{\operatorname{trace}(M^\intercal M)}.\end{align*}$$
If M is symmetric, then
![]() $\|M\|_{\mathrm F}^2$
is the sum of squares of the eigenvalues of M (with multiplicity).
$\|M\|_{\mathrm F}^2$
is the sum of squares of the eigenvalues of M (with multiplicity).
Famously, Eckart and Young [Reference Eckart and Young31] proved that for any real matrix M, the degree to which M can be approximated by a low-rank matrix
![]() $\widetilde M$
can be described in terms of the spectrum of M. The following statement is specialized to the setting of real symmetric matrices.
$\widetilde M$
can be described in terms of the spectrum of M. The following statement is specialized to the setting of real symmetric matrices.
Theorem 4.13. Consider a symmetric matrix
![]() $M\in \mathbb {R}^{n\times n}$
, and let
$M\in \mathbb {R}^{n\times n}$
, and let
![]() $\lambda _1,\ldots ,\lambda _n$
be its eigenvalues. Then for any
$\lambda _1,\ldots ,\lambda _n$
be its eigenvalues. Then for any
![]() $r=0,\ldots ,n$
we have
$r=0,\ldots ,n$
we have
 $$\begin{align*}\min_{\substack{\widetilde M\in\mathbb{R}^{n\times n}\\\operatorname{rank}(\widetilde M)\le r}}\|M-\widetilde M\|^2_{\mathrm F}=\min_{\substack{I\subseteq [n]\\|I|=n-r}}\sum_{i\in I}\lambda_{i}^2,\end{align*}$$
$$\begin{align*}\min_{\substack{\widetilde M\in\mathbb{R}^{n\times n}\\\operatorname{rank}(\widetilde M)\le r}}\|M-\widetilde M\|^2_{\mathrm F}=\min_{\substack{I\subseteq [n]\\|I|=n-r}}\sum_{i\in I}\lambda_{i}^2,\end{align*}$$
where the minimum is over all (not necessarily symmetricFootnote 8) matrices
![]() $\widetilde M\in \mathbb {R}^{n\times n}$
with rank at most r.
$\widetilde M\in \mathbb {R}^{n\times n}$
with rank at most r.
4.5 Analysis of Boolean functions
In this subsection, we collect some tools from the theory of Boolean functions. A thorough introduction to the subject can be found in [Reference O’Donnell81].
Consider a multilinear polynomial
![]() $f(x_1,\ldots ,x_n) = \sum _{S\subseteq [n]} a_S\prod _{i\in S}x_i$
. An easy computation shows that if
$f(x_1,\ldots ,x_n) = \sum _{S\subseteq [n]} a_S\prod _{i\in S}x_i$
. An easy computation shows that if
![]() $\vec x$
is a sequence of independent Rademacher or independent standard Gaussian random variables, then
$\vec x$
is a sequence of independent Rademacher or independent standard Gaussian random variables, then
![]() $\mathbb {E}[f(\vec x)]=a_{\emptyset }$
and
$\mathbb {E}[f(\vec x)]=a_{\emptyset }$
and
Thus, in the case
![]() $\deg f=2$
, we can consider the contributions to the variance
$\deg f=2$
, we can consider the contributions to the variance
![]() $\operatorname {Var}[f(\vec x)]$
coming from the ‘linear’ part and the ‘quadratic’ part. This will be important in our proof of Theorem 2.1.
$\operatorname {Var}[f(\vec x)]$
coming from the ‘linear’ part and the ‘quadratic’ part. This will be important in our proof of Theorem 2.1.
We will need the following bound on moments of low-degree polynomials of Rademacher or standard Gaussian random variables (which is a special case of a phenomenon called hypercontractivity).
Theorem 4.14 [Reference O’Donnell81, Theorem 9.21]
Let f be a polynomial in n variables of degree at most d. Let
![]() $\vec x=(x_1,\ldots ,x_n)$
either be a vector of independent Rademacher random variables or a vector of independent standard Gaussian random variables. Then for any real number
$\vec x=(x_1,\ldots ,x_n)$
either be a vector of independent Rademacher random variables or a vector of independent standard Gaussian random variables. Then for any real number
![]() $q\geq 2$
, we have
$q\geq 2$
, we have
We emphasize that we do not require
![]() $f(\vec x)$
to have mean zero, so in the general setting of Theorem 4.14 one does not necessarily have
$f(\vec x)$
to have mean zero, so in the general setting of Theorem 4.14 one does not necessarily have
![]() $\mathbb {E}[f(\vec x)^2]^{1/2}=\sigma (f(\vec x))$
(though in our proof of Theorem 2.1 we will only apply Theorem 4.14 in the case where
$\mathbb {E}[f(\vec x)^2]^{1/2}=\sigma (f(\vec x))$
(though in our proof of Theorem 2.1 we will only apply Theorem 4.14 in the case where
![]() $\mathbb {E}[f(\vec x)]=0$
).
$\mathbb {E}[f(\vec x)]=0$
).
Note that [Reference O’Donnell81, Theorem 9.21] is stated only for Rademacher random variables; the Gaussian case of Theorem 4.14 follows by approximating Gaussian random variables with sums of Rademacher random variables, using the central limit theorem.
Next, one can use Theorem 4.14 to obtain the following concentration inequality. The Rademacher case is stated as [Reference O’Donnell81, Theorem 9.23], and the Gaussian case may be proved in the same way.
Theorem 4.15. Let f be a polynomial in n variables of degree at most d. Let
![]() $\vec x=(x_1,\ldots ,x_n)$
either be a vector of independent Rademacher random variables or a vector of independent standard Gaussian random variables. Then for any
$\vec x=(x_1,\ldots ,x_n)$
either be a vector of independent Rademacher random variables or a vector of independent standard Gaussian random variables. Then for any
![]() $t\ge (2e)^{d/2}$
,
$t\ge (2e)^{d/2}$
,
 $$\begin{align*}\Pr\left[|f(\vec x)|\ge t(\mathbb{E}[f(x)^2])^{1/2}\right]\le \exp\left(-\frac{d}{2e} t^{2/d}\right).\end{align*}$$
$$\begin{align*}\Pr\left[|f(\vec x)|\ge t(\mathbb{E}[f(x)^2])^{1/2}\right]\le \exp\left(-\frac{d}{2e} t^{2/d}\right).\end{align*}$$
4.6 Basic concentration inequalities
We will frequently need the Chernoff bound for binomial and hypergeometric distributions (see, for example, [Reference Janson, Łuczak and Rucinski59, Theorems 2.1 and 2.10]). Recall that the hypergeometric distribution
![]() $\mathrm {Hyp}(N,K,n)$
is the distribution of
$\mathrm {Hyp}(N,K,n)$
is the distribution of
![]() $|Z\cap U|$
, for fixed sets
$|Z\cap U|$
, for fixed sets
![]() $U\subseteq S$
with
$U\subseteq S$
with
![]() $|S|=N$
and
$|S|=N$
and
![]() $|U|=K$
and a uniformly random size-n subset
$|U|=K$
and a uniformly random size-n subset
![]() $Z\subseteq S$
.
$Z\subseteq S$
.
Lemma 4.16 (Chernoff bound)
Let X be either:
-
• a sum of independent random variables, each of which take values in
 $\{0,1\}$
, or
$\{0,1\}$
, or -
• hypergeometrically distributed (with any parameters).
Then for any
![]() $\delta>0$
, we have
$\delta>0$
, we have
 $$ \begin{align*} \Pr[X\le (1-\delta)\mathbb{E}X]&\le\exp(-\delta^2\mathbb{E}X/2),\\ \Pr[X\ge (1+\delta)\mathbb{E}X]&\le\exp(-\delta^2\mathbb{E}X/(2+\delta)). \end{align*} $$
$$ \begin{align*} \Pr[X\le (1-\delta)\mathbb{E}X]&\le\exp(-\delta^2\mathbb{E}X/2),\\ \Pr[X\ge (1+\delta)\mathbb{E}X]&\le\exp(-\delta^2\mathbb{E}X/(2+\delta)). \end{align*} $$
We will also need the following concentration inequality, which is a simple consequence of the Azuma–Hoeffding martingale concentration inequality (a special case appears in [Reference Greenhill, Isaev, Kwan and McKay53, Corollary 2.2], and the general case follows from the same proof).
Lemma 4.17. Consider a partition
![]() $[n]=I_1\cup \cdots \cup I_m$
, and sequences
$[n]=I_1\cup \cdots \cup I_m$
, and sequences
![]() $(\ell _1,\ldots ,\ell _m), (\ell _1',\ldots ,\ell _m')\in \mathbb N^m$
with
$(\ell _1,\ldots ,\ell _m), (\ell _1',\ldots ,\ell _m')\in \mathbb N^m$
with
![]() $\ell _k+\ell ^{\prime }_k\leq |I_k|$
for
$\ell _k+\ell ^{\prime }_k\leq |I_k|$
for
![]() $k=1,\ldots ,m$
(and
$k=1,\ldots ,m$
(and
![]() $\ell _1+\cdots +\ell _m+\ell _1'+\cdots +\ell _m'>0$
). Let
$\ell _1+\cdots +\ell _m+\ell _1'+\cdots +\ell _m'>0$
). Let
![]() $S\subseteq \{-1,0,1\}^{n}$
be the set of vectors
$S\subseteq \{-1,0,1\}^{n}$
be the set of vectors
![]() $\vec {x}\in \{-1,0,1\}^{n}$
such that
$\vec {x}\in \{-1,0,1\}^{n}$
such that
![]() $\vec {x}_{I_k}$
has exactly
$\vec {x}_{I_k}$
has exactly
![]() $\ell _k$
entries being
$\ell _k$
entries being
![]() $1$
and exactly
$1$
and exactly
![]() $\ell _k'$
entries being
$\ell _k'$
entries being
![]() $-1$
for each
$-1$
for each
![]() $k=1,\ldots ,m$
. Let
$k=1,\ldots ,m$
. Let
![]() $a>0$
and suppose that
$a>0$
and suppose that
![]() $f\colon S\to \mathbb {R}$
is a function such that we have
$f\colon S\to \mathbb {R}$
is a function such that we have
![]() $|f(\vec {x})-f(\vec {x}')|\le a$
for any two vectors
$|f(\vec {x})-f(\vec {x}')|\le a$
for any two vectors
![]() $\vec {x}, \vec {x}'\in S$
which differ in precisely two coordinates (i.e., which are obtained from each other by switching two entries inside some set
$\vec {x}, \vec {x}'\in S$
which differ in precisely two coordinates (i.e., which are obtained from each other by switching two entries inside some set
![]() $I_k$
). Then for a uniformly random vector
$I_k$
). Then for a uniformly random vector
![]() $\vec {x}\in S$
and any
$\vec {x}\in S$
and any
![]() $t\geq 0$
we have
$t\geq 0$
we have
 $$\begin{align*}\Pr[|f(\vec{x})-\mathbb E f(\vec{x})|\ge t]\le2\exp\left(-\frac{t^{2}}{2\cdot (\ell_1+\cdots+\ell_m+\ell_1'+\cdots+\ell_m')\cdot a^2}\right).\end{align*}$$
$$\begin{align*}\Pr[|f(\vec{x})-\mathbb E f(\vec{x})|\ge t]\le2\exp\left(-\frac{t^{2}}{2\cdot (\ell_1+\cdots+\ell_m+\ell_1'+\cdots+\ell_m')\cdot a^2}\right).\end{align*}$$
Proof. We sample a uniformly random vector
![]() $\vec {x}\in S$
in
$\vec {x}\in S$
in
![]() $\ell :=\ell _1+\cdots +\ell _m+\ell _1'+\cdots +\ell _m'$
steps, as follows. In the first
$\ell :=\ell _1+\cdots +\ell _m+\ell _1'+\cdots +\ell _m'$
steps, as follows. In the first
![]() $\ell _1$
steps, we pick the
$\ell _1$
steps, we pick the
![]() $\ell _1$
indices
$\ell _1$
indices
![]() $i\in I_1$
such that
$i\in I_1$
such that
![]() $x_i=1$
(at each step, pick an index
$x_i=1$
(at each step, pick an index
![]() $i\in I_1$
uniformly at random among the indices where
$i\in I_1$
uniformly at random among the indices where
![]() $x_i$
is not yet defined, and define
$x_i$
is not yet defined, and define
![]() $x_i=1$
). In the next
$x_i=1$
). In the next
![]() $\ell _2$
steps, we pick the
$\ell _2$
steps, we pick the
![]() $\ell _2$
indices
$\ell _2$
indices
![]() $i\in I_2$
such that
$i\in I_2$
such that
![]() $x_i=1$
, and so on. After
$x_i=1$
, and so on. After
![]() $\ell _1+\cdots +\ell _m$
steps, we have defined all the
$\ell _1+\cdots +\ell _m$
steps, we have defined all the
![]() $1$
-entries of
$1$
-entries of
![]() $\vec {x}$
. Now, we repeat the procedure (for
$\vec {x}$
. Now, we repeat the procedure (for
![]() $\ell _1'+\cdots +\ell _m'$
steps) for the
$\ell _1'+\cdots +\ell _m'$
steps) for the
![]() $-1$
-entries.
$-1$
-entries.
For
![]() $t=0,\ldots ,\ell $
, define
$t=0,\ldots ,\ell $
, define
![]() $X_t$
to be the expectation of
$X_t$
to be the expectation of
![]() $f(\vec {x})$
conditioned on the coordinates of
$f(\vec {x})$
conditioned on the coordinates of
![]() $\vec {x}$
defined up to step t. Then
$\vec {x}$
defined up to step t. Then
![]() $X_0,\ldots ,X_t$
is the Doob martingale associated to our process of sampling
$X_0,\ldots ,X_t$
is the Doob martingale associated to our process of sampling
![]() $\vec {x}$
. Note that
$\vec {x}$
. Note that
![]() $X_0=\mathbb E f(\vec {x})$
and
$X_0=\mathbb E f(\vec {x})$
and
![]() $X_{\ell }=f(\vec {x})$
.
$X_{\ell }=f(\vec {x})$
.
We claim that we always have
![]() $|X_t-X_{t-1}|\le a$
for
$|X_t-X_{t-1}|\le a$
for
![]() $t=1,\ldots ,\ell $
. Indeed, let us condition on any outcomes of the first
$t=1,\ldots ,\ell $
. Indeed, let us condition on any outcomes of the first
![]() $t-1$
steps of our process of sampling
$t-1$
steps of our process of sampling
![]() $\vec {x}$
. Now, for any two possible indices i and
$\vec {x}$
. Now, for any two possible indices i and
![]() $i'$
chosen the t-th step, we can couple the possible outcomes of
$i'$
chosen the t-th step, we can couple the possible outcomes of
![]() $\vec {x}$
if i is chosen in the t-th step with the possible outcomes of
$\vec {x}$
if i is chosen in the t-th step with the possible outcomes of
![]() $\vec {x}$
if
$\vec {x}$
if
![]() $i'$
is chosen in the t-th step, simply by switching the i-th and the
$i'$
is chosen in the t-th step, simply by switching the i-th and the
![]() $i'$
-th coordinate. Using our assumption on f, this shows that for any two possible outcomes in the t-th step the corresponding conditional expectations differ by at most a. This implies
$i'$
-th coordinate. Using our assumption on f, this shows that for any two possible outcomes in the t-th step the corresponding conditional expectations differ by at most a. This implies
![]() $|X_t-X_{t-1}|\le a$
, as claimed.
$|X_t-X_{t-1}|\le a$
, as claimed.
Now, the inequality in the lemma follows from the Azuma–Hoeffding inequality for martingales (see, for example, [Reference Janson, Łuczak and Rucinski59, Theorem 2.25]).
5 Small-ball probability for quadratic polynomials of Gaussians
In this section, we prove Theorem 1.6, which we reproduce for the reader’s convenience. For the sake of convenience in the proofs and statements, in this section the notation
![]() $a\lesssim b$
simply means that
$a\lesssim b$
simply means that
![]() $a\le C b$
for some constant C (i.e., there is no stipulation that n, the number of variables, be large).
$a\le C b$
for some constant C (i.e., there is no stipulation that n, the number of variables, be large).
Theorem 1.6. Let
![]() $\vec Z = (Z_1,\ldots ,Z_n)\sim \mathcal {N}(0,1)^{\otimes n}$
be a vector of independent standard Gaussian random variables. Consider a real quadratic polynomial
$\vec Z = (Z_1,\ldots ,Z_n)\sim \mathcal {N}(0,1)^{\otimes n}$
be a vector of independent standard Gaussian random variables. Consider a real quadratic polynomial
![]() $f(\vec Z)$
of
$f(\vec Z)$
of
![]() $\vec Z$
, which we may write as
$\vec Z$
, which we may write as
for some nonzero symmetric matrix
![]() $F\in \mathbb {R}^{n\times n}$
, some vector
$F\in \mathbb {R}^{n\times n}$
, some vector
![]() $\vec f\in \mathbb {R}^n$
and some
$\vec f\in \mathbb {R}^n$
and some
![]() $f_0\in \mathbb {R}$
. Suppose that for some
$f_0\in \mathbb {R}$
. Suppose that for some
![]() $\eta>0$
we have
$\eta>0$
we have
 $$\begin{align*}\min_{\substack{\widetilde F\in\mathbb{R}^{n\times n}\\ \operatorname{rank}(\widetilde F)\le 2}}\frac{\|F-\widetilde F\|^2_{\mathrm F}}{\|F\|^2_{\mathrm{F}}}\ge \eta. \end{align*}$$
$$\begin{align*}\min_{\substack{\widetilde F\in\mathbb{R}^{n\times n}\\ \operatorname{rank}(\widetilde F)\le 2}}\frac{\|F-\widetilde F\|^2_{\mathrm F}}{\|F\|^2_{\mathrm{F}}}\ge \eta. \end{align*}$$
Then for any
![]() $\varepsilon> 0$
we have
$\varepsilon> 0$
we have
Remark 5.1. By Theorem 4.13, the robust rank assumption in Theorem 1.6 is equivalent to the assumption that every subset
![]() $I\subseteq [n]$
of size
$I\subseteq [n]$
of size
![]() $|I|=n-2$
satisfies
$|I|=n-2$
satisfies
![]() $\sum _{i\in I} \lambda _i^2\geq \eta (\lambda _1^2+\cdots +\lambda _n^2)$
, where
$\sum _{i\in I} \lambda _i^2\geq \eta (\lambda _1^2+\cdots +\lambda _n^2)$
, where
![]() $\lambda _1,\ldots ,\lambda _n$
denote the eigenvalues of F.
$\lambda _1,\ldots ,\lambda _n$
denote the eigenvalues of F.
We remark that for any real random variable X, one can use Chebyshev’s inequality to show that
![]() $\mathcal {L}(X,\varepsilon ) = \Omega (\varepsilon /\sigma (X))$
, so the bound in Theorem 1.6 is best-possible.
$\mathcal {L}(X,\varepsilon ) = \Omega (\varepsilon /\sigma (X))$
, so the bound in Theorem 1.6 is best-possible.
In the proof of Theorem 2.1, we will actually need a slightly more technical nonuniform version of Theorem 1.6 that decays away from the mean (at a high level, this is proved by combining Theorem 1.6 with the hypercontractive tail bound in Theorem 4.15, via a ‘splitting’ technique; for this splitting technique, we need our rank assumption to be slightly stronger than in Theorem 1.6). We will also need a lower bound on the probability that
![]() $f(\vec Z)$
falls in a given interval of length
$f(\vec Z)$
falls in a given interval of length
![]() $\varepsilon $
, as long as this interval is relatively close to
$\varepsilon $
, as long as this interval is relatively close to
![]() $\mathbb E f(\vec Z)$
, and lies on ‘the correct side’ of
$\mathbb E f(\vec Z)$
, and lies on ‘the correct side’ of
![]() $\mathbb E f(\vec Z)$
(this lower bound requires no rank assumption).
$\mathbb E f(\vec Z)$
(this lower bound requires no rank assumption).
Theorem 5.2. Let
![]() $\vec Z = (Z_1,\ldots ,Z_n)\sim \mathcal {N}(0,1)^{\otimes n}$
be a vector of independent standard Gaussian random variables. Consider a nonconstant real quadratic polynomial
$\vec Z = (Z_1,\ldots ,Z_n)\sim \mathcal {N}(0,1)^{\otimes n}$
be a vector of independent standard Gaussian random variables. Consider a nonconstant real quadratic polynomial
![]() $f(\vec Z)$
of
$f(\vec Z)$
of
![]() $\vec Z$
, which we may write as
$\vec Z$
, which we may write as
for some symmetric matrix
![]() $F\in \mathbb {R}^{n\times n}$
, some vector
$F\in \mathbb {R}^{n\times n}$
, some vector
![]() $\vec f\in \mathbb {R}^n$
and some
$\vec f\in \mathbb {R}^n$
and some
![]() $f_0\in \mathbb {R}$
.
$f_0\in \mathbb {R}$
.
-
1. Suppose that F is nonzero and
 $$\begin{align*}\min_{\substack{\widetilde F\in\mathbb{R}^{n\times n}\\ \operatorname{rank}(\widetilde F)\le 3}}\frac{\|F-\widetilde F\|^2_{\mathrm F}}{\|F\|^2_{\mathrm{F}}}\ge \eta.\end{align*}$$
$$\begin{align*}\min_{\substack{\widetilde F\in\mathbb{R}^{n\times n}\\ \operatorname{rank}(\widetilde F)\le 3}}\frac{\|F-\widetilde F\|^2_{\mathrm F}}{\|F\|^2_{\mathrm{F}}}\ge \eta.\end{align*}$$
Then for any
 $x\in \mathbb {R}$
and any
$x\in \mathbb {R}$
and any
 $0\le \varepsilon \le \sigma (f)$
, we have
$0\le \varepsilon \le \sigma (f)$
, we have  $$\begin{align*}\Pr[f-\mathbb E f \in [x, x+ \varepsilon]]\lesssim_{\eta}\frac{\varepsilon}{\sigma(f)}\exp\left(-\Omega\left(\frac{|x|}{\sigma(f)}\right)\right).\end{align*}$$
$$\begin{align*}\Pr[f-\mathbb E f \in [x, x+ \varepsilon]]\lesssim_{\eta}\frac{\varepsilon}{\sigma(f)}\exp\left(-\Omega\left(\frac{|x|}{\sigma(f)}\right)\right).\end{align*}$$
-
2. Let
 $\lambda _1, \ldots , \lambda _n$
be the eigenvalues of F. Suppose that
$\lambda _1, \ldots , \lambda _n$
be the eigenvalues of F. Suppose that
 $|\lambda _i|\leq \lambda _1$
for
$|\lambda _i|\leq \lambda _1$
for
 $i=1,\ldots ,n$
. Then for any
$i=1,\ldots ,n$
. Then for any
 $A>0$
and
$A>0$
and
 $0\le \varepsilon \le \sigma (f)$
, we have
$0\le \varepsilon \le \sigma (f)$
, we have  $$\begin{align*}\inf_{0\le x\le A\sigma(f)}\Pr[f-\mathbb E f\in[x,x+\varepsilon]] \gtrsim_A \frac{\varepsilon}{\sigma(f)}.\end{align*}$$
$$\begin{align*}\inf_{0\le x\le A\sigma(f)}\Pr[f-\mathbb E f\in[x,x+\varepsilon]] \gtrsim_A \frac{\varepsilon}{\sigma(f)}.\end{align*}$$
Remark 5.3. Note that the infimum in (2) is only over nonnegative x (this nonnegativity assumption corresponds to our implicit assumption that
![]() $\lambda _1\ge 0$
). A two-sided bound is not possible in general, as the polynomial
$\lambda _1\ge 0$
). A two-sided bound is not possible in general, as the polynomial
![]() $f(\vec Z)=Z_1^2$
shows. Also, while the rank assumption in Theorem 1.6 (robustly having rank at least 3) was best-possible, we believe that the rank assumption in Theorem 5.2(1) (robustly having rank at least 4) can be improved; it would be interesting to investigate this further (e.g., one might try to prove Theorem 5.2(1) directly rather than deducing it from Theorem 1.6 via our splitting technique).
$f(\vec Z)=Z_1^2$
shows. Also, while the rank assumption in Theorem 1.6 (robustly having rank at least 3) was best-possible, we believe that the rank assumption in Theorem 5.2(1) (robustly having rank at least 4) can be improved; it would be interesting to investigate this further (e.g., one might try to prove Theorem 5.2(1) directly rather than deducing it from Theorem 1.6 via our splitting technique).
In addition, in Theorem 5.2(2), the quantitative bound for implicit constant hidden by ‘
![]() $\gtrsim _A$
’ is rather poor; our proof provides a dependence of the form
$\gtrsim _A$
’ is rather poor; our proof provides a dependence of the form
![]() $\exp (-\exp (O(A^2)))$
. We believe that the correct dependence is
$\exp (-\exp (O(A^2)))$
. We believe that the correct dependence is
![]() $\exp (-O(A^2))$
, and it may be interesting to prove this.
$\exp (-O(A^2))$
, and it may be interesting to prove this.
By orthogonal diagonalization of F and the invariance of the distribution of
![]() $\vec Z$
under orthonormal transformations, in the proofs of Theorems 1.6 and 5.2 we can reduce to the case where
$\vec Z$
under orthonormal transformations, in the proofs of Theorems 1.6 and 5.2 we can reduce to the case where
![]() $f(\vec Z)=a_0+\sum _{i=1}^n (a_i Z_i+\lambda _iZ_i^2)$
for some
$f(\vec Z)=a_0+\sum _{i=1}^n (a_i Z_i+\lambda _iZ_i^2)$
for some
![]() $a_0,\ldots ,a_n\in \mathbb {R}$
. This is a sum of independent random variables, so we can proceed using Fourier-analytic techniques.
$a_0,\ldots ,a_n\in \mathbb {R}$
. This is a sum of independent random variables, so we can proceed using Fourier-analytic techniques.
The rest of this section proceeds as follows. First, in Section 5.1, we prove Lemma 5.5, which encapsulates certain Fourier-analytic estimates that are effective when no individual term
![]() $a_i Z_i+\lambda _iZ_i^2$
contributes too much to the variance of
$a_i Z_i+\lambda _iZ_i^2$
contributes too much to the variance of
![]() $f(\vec Z)$
(essentially, these are the estimates one needs for a central limit theorem).
$f(\vec Z)$
(essentially, these are the estimates one needs for a central limit theorem).
Second, in Section 5.2 we prove the uniform upper bound in Theorem 1.6. In the case where no individual term contributes too much to the variance of
![]() $f(\vec Z)$
, we use Lemma 5.5, and otherwise we need some more specialized Fourier-analytic computations.
$f(\vec Z)$
, we use Lemma 5.5, and otherwise we need some more specialized Fourier-analytic computations.
Third, in Section 5.3 we prove the lower bound in Theorem 5.2(2). Again, we use Lemma 5.5 in the case where no individual term contributes too much to the variance of
![]() $f(\vec Z)$
, while in the case where one of the terms is especially influential we perform an explicit (non-Fourier-analytic) computation.
$f(\vec Z)$
, while in the case where one of the terms is especially influential we perform an explicit (non-Fourier-analytic) computation.
Then, in Section 5.4 we deduce the nonuniform upper bound in Theorem 5.2(1) from Theorem 1.6, using a ‘splitting’ technique.
Finally, in Section 5.5 we prove an auxiliary technical estimate on characteristic functions of quadratic polynomials of Gaussian random variables, in terms of the ‘rank robustness’ of the quadratic polynomial (which we will need in the proof of Theorem 3.1).
5.1 Gaussian Fourier-analytic estimates
In this subsection, we prove several Fourier-analytic estimates. First, we state a formula for the absolute value of the characteristic function of a univariate quadratic polynomial of a Gaussian random variable. One can prove this by direct computation, but we instead give a quick deduction from the formula for the characteristic function of a noncentral chi-squared distribution (i.e., of a random variable
![]() $Z^2$
where
$Z^2$
where
![]() $Z\sim \mathcal {N}(\mu ,\sigma ^2)$
; see, for example, [Reference Patnaik82]).
$Z\sim \mathcal {N}(\mu ,\sigma ^2)$
; see, for example, [Reference Patnaik82]).
Lemma 5.4. Let
![]() $W\sim \mathcal N(0,1)$
, and let
$W\sim \mathcal N(0,1)$
, and let
![]() $X=a W+\lambda W^2$
for some
$X=a W+\lambda W^2$
for some
![]() $a,\lambda \in \mathbb {R}$
. We have
$a,\lambda \in \mathbb {R}$
. We have
 $$\begin{align*}|\varphi_X(t)| = \frac{\exp(-a^2t^2/(2+8\lambda^2t^2))}{(1+4\lambda^2t^2)^{1/4}}.\end{align*}$$
$$\begin{align*}|\varphi_X(t)| = \frac{\exp(-a^2t^2/(2+8\lambda^2t^2))}{(1+4\lambda^2t^2)^{1/4}}.\end{align*}$$
Proof. If
![]() $\lambda =0$
, then
$\lambda =0$
, then
![]() $\varphi _{X}(t)=\varphi _{aW}(t)=\varphi _W(at)=\exp (-a^2t^2/2)$
, as desired. So let us assume
$\varphi _{X}(t)=\varphi _{aW}(t)=\varphi _W(at)=\exp (-a^2t^2/2)$
, as desired. So let us assume
![]() $\lambda \neq 0$
. Note that
$\lambda \neq 0$
. Note that
![]() $X=a W+\lambda W^2 = \lambda (W + a/(2\lambda ))^2-a^2/(4\lambda )$
, and thus,
$X=a W+\lambda W^2 = \lambda (W + a/(2\lambda ))^2-a^2/(4\lambda )$
, and thus,
Using the formula for the characteristic function of a noncentral chi-squared distribution with
![]() $1$
degree of freedom and noncentrality parameter
$1$
degree of freedom and noncentrality parameter
![]() $(a/(2\lambda ))^2$
, we obtain
$(a/(2\lambda ))^2$
, we obtain
 $$\begin{align*}|\varphi_{(W + a/(2\lambda))^2}(\lambda t)| =\frac{\left|\exp\left(\frac{i\cdot a^2/(4\lambda^2)\cdot \lambda t}{1-2i\lambda t}\right)\right|}{|1-2i\lambda t|^{1/2}} =\frac{\left|\exp\left(\frac{i\cdot a^2/(4\lambda^2)\cdot \lambda t\cdot (1+2i\lambda t)}{1+4\lambda^2 t^2}\right)\right|}{(1+4\lambda^2 t^2)^{1/4}} =\frac{\exp\left(\frac{-a^2t^2}{2(1+4\lambda^2t^2)}\right)}{(1+4\lambda^2t^2)^{1/4}}. \end{align*}$$
$$\begin{align*}|\varphi_{(W + a/(2\lambda))^2}(\lambda t)| =\frac{\left|\exp\left(\frac{i\cdot a^2/(4\lambda^2)\cdot \lambda t}{1-2i\lambda t}\right)\right|}{|1-2i\lambda t|^{1/2}} =\frac{\left|\exp\left(\frac{i\cdot a^2/(4\lambda^2)\cdot \lambda t\cdot (1+2i\lambda t)}{1+4\lambda^2 t^2}\right)\right|}{(1+4\lambda^2 t^2)^{1/4}} =\frac{\exp\left(\frac{-a^2t^2}{2(1+4\lambda^2t^2)}\right)}{(1+4\lambda^2t^2)^{1/4}}. \end{align*}$$
The crucial estimates in this subsection are encapuslated in the following lemma.
Lemma 5.5. There exist constants
![]() $C_{5.5},C_{5.5}'>0$
such that the following holds. Let
$C_{5.5},C_{5.5}'>0$
such that the following holds. Let
![]() $W_1,\ldots ,W_n\sim \mathcal {N}(0,1)$
be independent standard Gaussian random variables, and fix sequences
$W_1,\ldots ,W_n\sim \mathcal {N}(0,1)$
be independent standard Gaussian random variables, and fix sequences
![]() $\vec a,\vec \lambda \in \mathbb {R}^n$
not both zero. Define random variables
$\vec a,\vec \lambda \in \mathbb {R}^n$
not both zero. Define random variables
![]() $X_1,\ldots ,X_n$
and X as well as nonnegative
$X_1,\ldots ,X_n$
and X as well as nonnegative
![]() $\sigma _1,\ldots ,\sigma _n, \sigma , \Gamma \in \mathbb {R}$
by
$\sigma _1,\ldots ,\sigma _n, \sigma , \Gamma \in \mathbb {R}$
by
 $$\begin{align*}X_i = a_iW_i + \lambda_i (W_i^2-1),\quad\!\! X=\sum_{i=1}^n X_i,\quad\!\! \sigma_i^2 = \sigma(X_i)^2= a_i^2 + 2\lambda_i^2, \quad\!\! \sigma^2 = \sum_{i=1}^n\sigma_i^2,\quad\!\! \Gamma=\frac{\sigma^{3}}{\sum_{i=1}^n\sigma_i^3}.\end{align*}$$
$$\begin{align*}X_i = a_iW_i + \lambda_i (W_i^2-1),\quad\!\! X=\sum_{i=1}^n X_i,\quad\!\! \sigma_i^2 = \sigma(X_i)^2= a_i^2 + 2\lambda_i^2, \quad\!\! \sigma^2 = \sum_{i=1}^n\sigma_i^2,\quad\!\! \Gamma=\frac{\sigma^{3}}{\sum_{i=1}^n\sigma_i^3}.\end{align*}$$
-
(a) If
 $\int _{-\infty }^{\infty }\prod _{i=1}^{n}|\varphi _{X_i}(t)|\,dt<\infty $
, then X has a continuous density function
$\int _{-\infty }^{\infty }\prod _{i=1}^{n}|\varphi _{X_i}(t)|\,dt<\infty $
, then X has a continuous density function
 $p_X\colon \mathbb {R}\to \mathbb {R}_{\ge 0}$
satisfying
$p_X\colon \mathbb {R}\to \mathbb {R}_{\ge 0}$
satisfying  $$\begin{align*}\sup_{u\in\mathbb{R}}\bigg|p_{X}(u)-\frac{e^{-u^2/(2\sigma^2)}}{\sigma\sqrt{2\pi}}\bigg|\le C_{5.5}\bigg( \frac{1}{\Gamma\sigma} + \int_{|t|\ge \Gamma/(32\sigma)}\prod_{i=1}^{n}|\varphi_{X_i}(t)|\,dt\bigg).\end{align*}$$
$$\begin{align*}\sup_{u\in\mathbb{R}}\bigg|p_{X}(u)-\frac{e^{-u^2/(2\sigma^2)}}{\sigma\sqrt{2\pi}}\bigg|\le C_{5.5}\bigg( \frac{1}{\Gamma\sigma} + \int_{|t|\ge \Gamma/(32\sigma)}\prod_{i=1}^{n}|\varphi_{X_i}(t)|\,dt\bigg).\end{align*}$$
-
(b) If
 $\sigma _i^2\le \sigma ^2/4$
for all
$\sigma _i^2\le \sigma ^2/4$
for all
 $i=1,\ldots , n$
, then for any
$i=1,\ldots , n$
, then for any
 $K>0$
, we have
$K>0$
, we have  $$\begin{align*}\int_{|t|\ge K/\sigma}\;\prod_{i=1}^{n}|\varphi_{X_i}(t)|\,dt\le \frac{C_{5.5}'}{K\sigma}.\end{align*}$$
$$\begin{align*}\int_{|t|\ge K/\sigma}\;\prod_{i=1}^{n}|\varphi_{X_i}(t)|\,dt\le \frac{C_{5.5}'}{K\sigma}.\end{align*}$$
Remark 5.6. Note that
![]() $\sigma ^3 = \sum _{i=1}^{n}\sigma _i^2\cdot \sigma \ge \sum _{i=1}^{n}\sigma _i^3$
and therefore
$\sigma ^3 = \sum _{i=1}^{n}\sigma _i^2\cdot \sigma \ge \sum _{i=1}^{n}\sigma _i^3$
and therefore
![]() $\Gamma \ge 1$
.
$\Gamma \ge 1$
.
The first part follows essentially immediately from the classical proof of the central limit theorem (see, for example, [Reference Petrov and Brown83]).
Proof of Lemma 5.5(a)
First, note that we may assume that there are no indices i with
![]() $\sigma _i=0$
(indeed, if
$\sigma _i=0$
(indeed, if
![]() $\sigma _i=0$
, then
$\sigma _i=0$
, then
![]() $\lambda _i=a_i=0$
and we can just omit all such indices). By rescaling, we may assume that
$\lambda _i=a_i=0$
and we can just omit all such indices). By rescaling, we may assume that
![]() $\sigma ^2 = 1$
. Note that
$\sigma ^2 = 1$
. Note that
![]() $\varphi _{X}(t)=\prod _{i=1}^{n}\varphi _{X_i}(t)$
, and hence
$\varphi _{X}(t)=\prod _{i=1}^{n}\varphi _{X_i}(t)$
, and hence
![]() $\int _{-\infty }^{\infty }|\varphi _{X}(t)|\,dt<\infty $
. Also recall that the standard Gaussian distribution has density
$\int _{-\infty }^{\infty }|\varphi _{X}(t)|\,dt<\infty $
. Also recall that the standard Gaussian distribution has density
![]() $u\mapsto e^{-u^2/2}/\sqrt {2\pi }$
and characteristic function
$u\mapsto e^{-u^2/2}/\sqrt {2\pi }$
and characteristic function
![]() $t\mapsto e^{-t^2/2}$
. Thus, by the inversion formula (4.1), it suffices to show that
$t\mapsto e^{-t^2/2}$
. Thus, by the inversion formula (4.1), it suffices to show that
 $$ \begin{align} \frac{1}{2\pi}\int_{-\infty}^{\infty}\bigg|\prod_{i=1}^{n}\varphi_{X_i}(t) - e^{-t^2/2}\bigg|\,dt\lesssim \frac1\Gamma + \int_{|t|\ge \Gamma/32}\;\prod_{i=1}^{n}|\varphi_{X_i}(t)|\,dt. \end{align} $$
$$ \begin{align} \frac{1}{2\pi}\int_{-\infty}^{\infty}\bigg|\prod_{i=1}^{n}\varphi_{X_i}(t) - e^{-t^2/2}\bigg|\,dt\lesssim \frac1\Gamma + \int_{|t|\ge \Gamma/32}\;\prod_{i=1}^{n}|\varphi_{X_i}(t)|\,dt. \end{align} $$
Note that
![]() $\mathbb E [X_i]=0$
for
$\mathbb E [X_i]=0$
for
![]() $i=1,\ldots ,n$
, and let us write
$i=1,\ldots ,n$
, and let us write
![]() $L=(\sum _{i=1}^{n}\mathbb {E}[|X_i|^3])/(\sum _{i=1}^n \sigma _i^{2})^{3/2}=\sum _{i=1}^{n}\mathbb {E}[|X_i|^3]$
. Then for
$L=(\sum _{i=1}^{n}\mathbb {E}[|X_i|^3])/(\sum _{i=1}^n \sigma _i^{2})^{3/2}=\sum _{i=1}^{n}\mathbb {E}[|X_i|^3]$
. Then for
![]() $|t|\le 1/(4L)$
, by [Reference Petrov and Brown83, Chapter V, Lemma 1] (which is a standard estimate in proofs of central limit theorems) we have
$|t|\le 1/(4L)$
, by [Reference Petrov and Brown83, Chapter V, Lemma 1] (which is a standard estimate in proofs of central limit theorems) we have
 $$\begin{align*}\bigg|\prod_{i=1}^{n}\varphi_{X_i}(t) - e^{-t^2/2}\bigg|=\left|\varphi_{X}(t) - e^{-t^2/2}\right|\le 16L\cdot |t|^3e^{-t^2/3}.\end{align*}$$
$$\begin{align*}\bigg|\prod_{i=1}^{n}\varphi_{X_i}(t) - e^{-t^2/2}\bigg|=\left|\varphi_{X}(t) - e^{-t^2/2}\right|\le 16L\cdot |t|^3e^{-t^2/3}.\end{align*}$$
By Hölder’s inequality and Theorem 4.14 (hypercontractivity), we have
![]() $\sigma _i^{3}\le \mathbb {E}[|X_i|^{3}]\le 8\sigma _i^{3}$
for
$\sigma _i^{3}\le \mathbb {E}[|X_i|^{3}]\le 8\sigma _i^{3}$
for
![]() $i=1,\ldots ,n$
, so we obtain
$i=1,\ldots ,n$
, so we obtain
![]() $1/\Gamma \leq L\leq 8/\Gamma $
. Thus, the interval
$1/\Gamma \leq L\leq 8/\Gamma $
. Thus, the interval
![]() $|t|\le \Gamma /32$
contributes at most
$|t|\le \Gamma /32$
contributes at most
![]() $\int _{-\Gamma /32}^{\Gamma /32}16L\cdot |t|^3e^{-t^2/3}\,dt\lesssim L\int _{-\infty }^{\infty }|t|^3e^{-t^2/3}\,dt \lesssim L\lesssim 1/\Gamma $
to the integral in (5.1). Therefore, we obtain
$\int _{-\Gamma /32}^{\Gamma /32}16L\cdot |t|^3e^{-t^2/3}\,dt\lesssim L\int _{-\infty }^{\infty }|t|^3e^{-t^2/3}\,dt \lesssim L\lesssim 1/\Gamma $
to the integral in (5.1). Therefore, we obtain
 $$ \begin{align*} \int_{|t|\ge {\Gamma}/{32}}\bigg|\prod_{i=1}^{n}\varphi_{X_i}(t) - e^{-t^2/2}\bigg|\,dt&\le \int_{|t|\ge {\Gamma}/{32}}e^{-t^2/2} + \bigg|\prod_{i=1}^{n}\varphi_{X_i}(t)\bigg|\,dt\\ &\lesssim \frac{1}{\Gamma} + \int_{|t|\ge {\Gamma}/{32}} \bigg|\prod_{i=1}^{n}\varphi_{X_i}(t)\bigg|\,dt. \\[-45pt] \end{align*} $$
$$ \begin{align*} \int_{|t|\ge {\Gamma}/{32}}\bigg|\prod_{i=1}^{n}\varphi_{X_i}(t) - e^{-t^2/2}\bigg|\,dt&\le \int_{|t|\ge {\Gamma}/{32}}e^{-t^2/2} + \bigg|\prod_{i=1}^{n}\varphi_{X_i}(t)\bigg|\,dt\\ &\lesssim \frac{1}{\Gamma} + \int_{|t|\ge {\Gamma}/{32}} \bigg|\prod_{i=1}^{n}\varphi_{X_i}(t)\bigg|\,dt. \\[-45pt] \end{align*} $$
To prove Lemma 5.5(b), we use Hölder’s inequality and Lemma 5.4.
Proof of Lemma 5.5(b)
As before, we may assume that there are no indices i with
![]() $\sigma _i=0$
, and by rescaling we may assume that
$\sigma _i=0$
, and by rescaling we may assume that
![]() $\sigma ^2 = 1$
. Via Lemma 5.4, we estimate
$\sigma ^2 = 1$
. Via Lemma 5.4, we estimate
 $$ \begin{align*} \int_{|t|\ge K}\bigg|\prod_{i=1}^{n}\varphi_{X_i}(t)\bigg|\,dt &\le \prod_{i=1}^{n}\bigg(\int_{|t|\ge K}|\varphi_{X_i}(t)|^{1/\sigma_i^2}\,dt\bigg)^{\sigma_i^2}\\ &=\prod_{i=1}^{n}\Bigg(\int_{|t|\ge K}\frac{\exp\Big(-{a_i^2t^2}/\left({(2+8\lambda_i^2t^2)\sigma_i^2}\right)\Big)}{(1+4\lambda_i^2t^2)^{1/(4\sigma_i^2)}}\,dt\Bigg)^{\sigma_i^2}\\ &\le\prod_{i=1}^{n}\Bigg(\int_{|t|\ge K}\frac{\exp\Big(-{a_i^2t^2}/\left({(2+8\lambda_i^2t^2)\sigma_i^2}\right)\Big)}{1+\lambda_i^2t^2/\sigma_i^2}\,dt\Bigg)^{\sigma_i^2}. \end{align*} $$
$$ \begin{align*} \int_{|t|\ge K}\bigg|\prod_{i=1}^{n}\varphi_{X_i}(t)\bigg|\,dt &\le \prod_{i=1}^{n}\bigg(\int_{|t|\ge K}|\varphi_{X_i}(t)|^{1/\sigma_i^2}\,dt\bigg)^{\sigma_i^2}\\ &=\prod_{i=1}^{n}\Bigg(\int_{|t|\ge K}\frac{\exp\Big(-{a_i^2t^2}/\left({(2+8\lambda_i^2t^2)\sigma_i^2}\right)\Big)}{(1+4\lambda_i^2t^2)^{1/(4\sigma_i^2)}}\,dt\Bigg)^{\sigma_i^2}\\ &\le\prod_{i=1}^{n}\Bigg(\int_{|t|\ge K}\frac{\exp\Big(-{a_i^2t^2}/\left({(2+8\lambda_i^2t^2)\sigma_i^2}\right)\Big)}{1+\lambda_i^2t^2/\sigma_i^2}\,dt\Bigg)^{\sigma_i^2}. \end{align*} $$
In the first step, we have used Hölder’s inequality with weights
![]() $\sigma _1^2,\ldots ,\sigma _n^2$
(which sum to 1) and in the final step we have used Bernoulli’s inequality (which says that
$\sigma _1^2,\ldots ,\sigma _n^2$
(which sum to 1) and in the final step we have used Bernoulli’s inequality (which says that
![]() $(1+x)^r\ge 1+rx$
for
$(1+x)^r\ge 1+rx$
for
![]() $x\ge 0$
and
$x\ge 0$
and
![]() $r\ge 1$
; recall that we are assuming that
$r\ge 1$
; recall that we are assuming that
![]() $4(a_i^2+2\lambda _i^2)=4\sigma _i^2\le 1$
for each i).
$4(a_i^2+2\lambda _i^2)=4\sigma _i^2\le 1$
for each i).
Since
![]() $\sum _{i=1}^n\sigma _i^2=1$
, it now suffices to prove that for each
$\sum _{i=1}^n\sigma _i^2=1$
, it now suffices to prove that for each
![]() $i=1,\ldots ,n$
we have
$i=1,\ldots ,n$
we have
 $$\begin{align*}\int_{|t|\ge K}\frac{\exp\Big(-{a_i^2t^2}/\left({(2+8\lambda_i^2t^2)\sigma_i^2}\right)\Big)}{1+\lambda_i^2t^2/\sigma_i^2}\,dt\lesssim \frac{1}{K}. \end{align*}$$
$$\begin{align*}\int_{|t|\ge K}\frac{\exp\Big(-{a_i^2t^2}/\left({(2+8\lambda_i^2t^2)\sigma_i^2}\right)\Big)}{1+\lambda_i^2t^2/\sigma_i^2}\,dt\lesssim \frac{1}{K}. \end{align*}$$
Fix some i. If
![]() $|\lambda _i|\ge |a_i|$
, then
$|\lambda _i|\ge |a_i|$
, then
![]() $\lambda _i^2\geq \sigma _i^2/3$
and
$\lambda _i^2\geq \sigma _i^2/3$
and
 $$\begin{align*}\int_{|t|\ge K}\frac{\exp\Big(-{a_i^2t^2}/\left({(2+8\lambda_i^2t^2)\sigma_i^2}\right)\Big)}{1+\lambda_i^2t^2/\sigma_i^2}\,dt\le\int_{|t|\ge K}\frac{1}{1+t^2/3}\,dt\lesssim \frac{1}{K}.\end{align*}$$
$$\begin{align*}\int_{|t|\ge K}\frac{\exp\Big(-{a_i^2t^2}/\left({(2+8\lambda_i^2t^2)\sigma_i^2}\right)\Big)}{1+\lambda_i^2t^2/\sigma_i^2}\,dt\le\int_{|t|\ge K}\frac{1}{1+t^2/3}\,dt\lesssim \frac{1}{K}.\end{align*}$$
Otherwise, if
![]() $|a_i|\ge |\lambda _i|$
, we have
$|a_i|\ge |\lambda _i|$
, we have
![]() $a_i^2\geq \sigma _i^2/3$
,
$a_i^2\geq \sigma _i^2/3$
,
![]() $\sigma _i^2\le 1$
, and therefore
$\sigma _i^2\le 1$
, and therefore
 $$ \begin{align*} \frac{\exp\Big(-{a_i^2t^2}/\left({(2+8\lambda_i^2t^2)\sigma_i^2}\right)\Big)}{1+\lambda_i^2t^2/\sigma_i^2}&\le \frac{\Big(1+{a_i^2t^2}/\left({(2+8\lambda_i^2t^2)\sigma_i^2}\right)\Big)^{-1}}{1+\lambda_i^2t^2/\sigma_i^2}\\ &\lesssim \frac{\big(1+{t^2}/({1+\lambda_i^2t^2})\big)^{-1}}{1+\lambda_i^2t^2/\sigma_i^2}\\ &\le \frac{\big(1+{t^2}/{(1+\lambda_i^2t^2)}\big)^{-1}}{1+\lambda_i^2t^2} = \frac{1}{1+(1+\lambda_i^2)t^2}. \end{align*} $$
$$ \begin{align*} \frac{\exp\Big(-{a_i^2t^2}/\left({(2+8\lambda_i^2t^2)\sigma_i^2}\right)\Big)}{1+\lambda_i^2t^2/\sigma_i^2}&\le \frac{\Big(1+{a_i^2t^2}/\left({(2+8\lambda_i^2t^2)\sigma_i^2}\right)\Big)^{-1}}{1+\lambda_i^2t^2/\sigma_i^2}\\ &\lesssim \frac{\big(1+{t^2}/({1+\lambda_i^2t^2})\big)^{-1}}{1+\lambda_i^2t^2/\sigma_i^2}\\ &\le \frac{\big(1+{t^2}/{(1+\lambda_i^2t^2)}\big)^{-1}}{1+\lambda_i^2t^2} = \frac{1}{1+(1+\lambda_i^2)t^2}. \end{align*} $$
It follows that
 $$ \begin{align*} &\int_{|t|\ge K}\frac{\exp\Big(-{a_i^2t^2}/\left({(2+8\lambda_i^2t^2)\sigma_i^2}\right)\Big)}{1+\lambda_i^2t^2/\sigma_i^2}\,dt \lesssim \int_{|t|\ge K}\frac{1}{1+(1+\lambda_i^2)t^2}\,dt \lesssim \frac{1}{K}.\\[-46pt] \end{align*} $$
$$ \begin{align*} &\int_{|t|\ge K}\frac{\exp\Big(-{a_i^2t^2}/\left({(2+8\lambda_i^2t^2)\sigma_i^2}\right)\Big)}{1+\lambda_i^2t^2/\sigma_i^2}\,dt \lesssim \int_{|t|\ge K}\frac{1}{1+(1+\lambda_i^2)t^2}\,dt \lesssim \frac{1}{K}.\\[-46pt] \end{align*} $$
5.2 Uniform anticoncentration
In this subsection, we prove Theorem 1.6. The crucial ingredient is the following Fourier-analytic estimate.
Lemma 5.7. Recall the definitions and notation in the statement of Lemma 5.5, and fix a parameter
![]() $\eta>0$
. Suppose that
$\eta>0$
. Suppose that
![]() $n\ge 2$
and
$n\ge 2$
and
![]() $\sum _{i\in I}\lambda _i^2\ge \eta \lambda _j^2$
for all
$\sum _{i\in I}\lambda _i^2\ge \eta \lambda _j^2$
for all
![]() $I\subseteq [n]$
with
$I\subseteq [n]$
with
![]() $|I|= n-2$
and all
$|I|= n-2$
and all
![]() $j\in [n]$
. Then
$j\in [n]$
. Then
 $$\begin{align*}\int_{|t|\ge 1/(32\sigma)}\prod_{i=1}^{n}|\varphi_{X_i}(t)|\,dt\lesssim_{\eta} \frac{1}{\sigma}.\end{align*}$$
$$\begin{align*}\int_{|t|\ge 1/(32\sigma)}\prod_{i=1}^{n}|\varphi_{X_i}(t)|\,dt\lesssim_{\eta} \frac{1}{\sigma}.\end{align*}$$
Proof. We may assume without loss of generality that
![]() $|\lambda _1|\geq \cdots \geq |\lambda _n|$
. By adding at most two terms with
$|\lambda _1|\geq \cdots \geq |\lambda _n|$
. By adding at most two terms with
![]() $a_i=\lambda _i=0$
, we may assume n is divisible by
$a_i=\lambda _i=0$
, we may assume n is divisible by
![]() $3$
. Note that if
$3$
. Note that if
![]() $\sigma _i^2\le \sigma ^2/4$
for all
$\sigma _i^2\le \sigma ^2/4$
for all
![]() $i\in [n]$
, the result follows immediately from Lemma 5.5(b). Therefore, it suffices to consider the case when there is an index j such that
$i\in [n]$
, the result follows immediately from Lemma 5.5(b). Therefore, it suffices to consider the case when there is an index j such that
![]() $\sigma _j^2\ge \sigma ^2/4$
.
$\sigma _j^2\ge \sigma ^2/4$
.
Note that the given condition implies
![]() $\sum _{k=1}^{n/3}\lambda _{3k}^2\ge \frac {1}{3}\sum _{k= 3}^{n}\lambda _k^2\ge \eta \lambda _j^2/3$
. Now, Lemma 5.4 yields
$\sum _{k=1}^{n/3}\lambda _{3k}^2\ge \frac {1}{3}\sum _{k= 3}^{n}\lambda _k^2\ge \eta \lambda _j^2/3$
. Now, Lemma 5.4 yields
 $$ \begin{align*} \prod_{i=1}^{n}|\varphi_{X_i}(t)|&\le \exp\bigg(\frac{-a_j^2t^2}{2+8\lambda_j^2t^2}\bigg)\prod_{i=1}^{n}\frac{1}{(1+4\lambda_i^2t^2)^{1/4}}\le \exp\bigg(\frac{-a_j^2t^2}{2+8\lambda_j^2t^2}\bigg)\prod_{i=1}^{n/3}\frac{1}{(1+4\lambda_{3i}^2t^2)^{3/4}}\\ &\le \exp\bigg(\frac{-a_j^2t^2}{2+8\lambda_j^2t^2}\bigg)\bigg(1+4\sum_{i=1}^{n/3}\lambda_{3i}^2t^2\bigg)^{-3/4}\le \exp\bigg(\frac{-a_j^2t^2}{2+8\lambda_j^2t^2}\bigg)(1+\eta \lambda_j^2t^2)^{-3/4}\\ &\le \bigg(1 + \frac{a_j^2t^2}{2+8\lambda_j^2t^2}\bigg)^{-3/4}(1+\eta\lambda_j^2t^2)^{-3/4}\\ &\lesssim_{\eta} (\lambda_j^2t^2+a_j^2t^2)^{-3/4}\lesssim (\sigma_j |t|)^{-3/2}\lesssim (\sigma |t|)^{-3/2}. \end{align*} $$
$$ \begin{align*} \prod_{i=1}^{n}|\varphi_{X_i}(t)|&\le \exp\bigg(\frac{-a_j^2t^2}{2+8\lambda_j^2t^2}\bigg)\prod_{i=1}^{n}\frac{1}{(1+4\lambda_i^2t^2)^{1/4}}\le \exp\bigg(\frac{-a_j^2t^2}{2+8\lambda_j^2t^2}\bigg)\prod_{i=1}^{n/3}\frac{1}{(1+4\lambda_{3i}^2t^2)^{3/4}}\\ &\le \exp\bigg(\frac{-a_j^2t^2}{2+8\lambda_j^2t^2}\bigg)\bigg(1+4\sum_{i=1}^{n/3}\lambda_{3i}^2t^2\bigg)^{-3/4}\le \exp\bigg(\frac{-a_j^2t^2}{2+8\lambda_j^2t^2}\bigg)(1+\eta \lambda_j^2t^2)^{-3/4}\\ &\le \bigg(1 + \frac{a_j^2t^2}{2+8\lambda_j^2t^2}\bigg)^{-3/4}(1+\eta\lambda_j^2t^2)^{-3/4}\\ &\lesssim_{\eta} (\lambda_j^2t^2+a_j^2t^2)^{-3/4}\lesssim (\sigma_j |t|)^{-3/2}\lesssim (\sigma |t|)^{-3/2}. \end{align*} $$
Thus, we have
 $$\begin{align*}\int_{|t|\ge 1/(32\sigma)}\prod_{i=1}^{n}|\varphi_{X_i}(t)|\,dt\lesssim_{\eta}\int_{|t|\ge 1/(32\sigma)}(\sigma |t|)^{-3/2}\,dt\lesssim 1/\sigma.\\[-47pt] \end{align*}$$
$$\begin{align*}\int_{|t|\ge 1/(32\sigma)}\prod_{i=1}^{n}|\varphi_{X_i}(t)|\,dt\lesssim_{\eta}\int_{|t|\ge 1/(32\sigma)}(\sigma |t|)^{-3/2}\,dt\lesssim 1/\sigma.\\[-47pt] \end{align*}$$
The proof of Theorem 1.6 is now immediate.
Proof of Theorem 1.6
By rescaling, we may assume
![]() $\sigma (f)=1$
. It suffices to show that the probability density function
$\sigma (f)=1$
. It suffices to show that the probability density function
![]() $p_{f-\mathbb E f}$
of
$p_{f-\mathbb E f}$
of
![]() $f-\mathbb Ef$
satisfies
$f-\mathbb Ef$
satisfies
![]() $p_{f-\mathbb E f}(u)\lesssim _{\eta } 1$
for all u.
$p_{f-\mathbb E f}(u)\lesssim _{\eta } 1$
for all u.
Since F is a real symmetric matrix, we can write
![]() $F = QD Q^{\intercal }$
, where D is a diagonal matrix with entries
$F = QD Q^{\intercal }$
, where D is a diagonal matrix with entries
![]() $\lambda _1,\ldots ,\lambda _n$
and Q is an orthogonal matrix. Let
$\lambda _1,\ldots ,\lambda _n$
and Q is an orthogonal matrix. Let
![]() $\vec W=Q^{\intercal }\vec Z$
, and note that
$\vec W=Q^{\intercal }\vec Z$
, and note that
![]() $\vec W$
is also distributed as
$\vec W$
is also distributed as
![]() $\mathcal {N}(0,1)^{\otimes n}$
(since the distribution
$\mathcal {N}(0,1)^{\otimes n}$
(since the distribution
![]() $\mathcal {N}(0,1)^{\otimes n}$
is invariant under orthogonal transformations). We have
$\mathcal {N}(0,1)^{\otimes n}$
is invariant under orthogonal transformations). We have
Let
![]() $\vec {a} = (a_1,\ldots ,a_n)=Q^\intercal \vec {f}$
. We have
$\vec {a} = (a_1,\ldots ,a_n)=Q^\intercal \vec {f}$
. We have
 $$\begin{align*}f-\mathbb E f= \sum_{i=1}^n(a_iW_i+\lambda_i(W_i^2-1)). \end{align*}$$
$$\begin{align*}f-\mathbb E f= \sum_{i=1}^n(a_iW_i+\lambda_i(W_i^2-1)). \end{align*}$$
Let
![]() $\sigma _1,\ldots ,\sigma _n\geq 0$
be such that
$\sigma _1,\ldots ,\sigma _n\geq 0$
be such that
![]() $\sigma _i^2=a_i^2+2\lambda _i^2$
, so
$\sigma _i^2=a_i^2+2\lambda _i^2$
, so
![]() $1=\sigma (f)^2 = \sigma _1^2+\cdots +\sigma _n^2$
. Note that the assumption in the theorem statement implies
$1=\sigma (f)^2 = \sigma _1^2+\cdots +\sigma _n^2$
. Note that the assumption in the theorem statement implies
![]() $n\ge 3$
, and combining the assumption with Theorem 4.13 yields
$n\ge 3$
, and combining the assumption with Theorem 4.13 yields
 $$\begin{align*}\eta\le \min_{\substack{\widetilde F\in\mathbb{R}^{n\times n}\\\operatorname{rank}(\widetilde F)\le 2}}\frac{\|F-\widetilde F\|^2_{\mathrm F}}{\|F\|^2_{\mathrm{F}}}=\min_{\substack{I\subseteq [n]\\|I|=n-2}} \frac{\sum_{i\in I}\lambda_i^2}{\lambda_1^2+\cdots+\lambda_n^2}.\end{align*}$$
$$\begin{align*}\eta\le \min_{\substack{\widetilde F\in\mathbb{R}^{n\times n}\\\operatorname{rank}(\widetilde F)\le 2}}\frac{\|F-\widetilde F\|^2_{\mathrm F}}{\|F\|^2_{\mathrm{F}}}=\min_{\substack{I\subseteq [n]\\|I|=n-2}} \frac{\sum_{i\in I}\lambda_i^2}{\lambda_1^2+\cdots+\lambda_n^2}.\end{align*}$$
Hence, for any subset
![]() $I\subseteq [n]$
with
$I\subseteq [n]$
with
![]() $|I|= n-2$
and any
$|I|= n-2$
and any
![]() $j\in [n]$
we obtain
$j\in [n]$
we obtain
![]() $\sum _{i\in I}\lambda _i^2\ge \eta (\lambda _1^2+\,\cdots\, +\lambda _n^2)\geq \eta \lambda _j^2$
. Let
$\sum _{i\in I}\lambda _i^2\ge \eta (\lambda _1^2+\,\cdots\, +\lambda _n^2)\geq \eta \lambda _j^2$
. Let
![]() $\Gamma $
be as in Lemma 5.5, and recall that
$\Gamma $
be as in Lemma 5.5, and recall that
![]() $\Gamma \ge 1$
.
$\Gamma \ge 1$
.
Now, by combining Lemma 5.5(a) and Lemma 5.7, we have that
 $$ \begin{align*} \sup_{u\in\mathbb{R}}p_{f}(u)=\sup_{u\in\mathbb{R}}p_{f-\mathbb E f}(u)\lesssim \frac{1}{\sqrt{2\pi}} + \frac{1}{\Gamma} + \int_{|t|\ge \Gamma/32}\prod_{i=1}^{n}|\varphi_{X_i}(t)|\,dt\lesssim_{\eta} 1. \end{align*} $$
$$ \begin{align*} \sup_{u\in\mathbb{R}}p_{f}(u)=\sup_{u\in\mathbb{R}}p_{f-\mathbb E f}(u)\lesssim \frac{1}{\sqrt{2\pi}} + \frac{1}{\Gamma} + \int_{|t|\ge \Gamma/32}\prod_{i=1}^{n}|\varphi_{X_i}(t)|\,dt\lesssim_{\eta} 1. \end{align*} $$
By integrating over the desired interval, we obtain the bound in Theorem 1.6.
5.3 Lower bounds on small-ball probabilities
Let us now prove the lower bound in Theorem 5.2(2). Note that Lemma 5.5(b) does not apply when some
![]() $\sigma _i$
is especially influential; in that case, we will use the following bare-hands estimate.
$\sigma _i$
is especially influential; in that case, we will use the following bare-hands estimate.
Lemma 5.8. Fix
![]() $A'\geq 1$
, and let
$A'\geq 1$
, and let
![]() $W\sim \mathcal N(0,1)$
and for some
$W\sim \mathcal N(0,1)$
and for some
![]() $a,\lambda \in \mathbb {R}$
(not both zero) let
$a,\lambda \in \mathbb {R}$
(not both zero) let
![]() $X=aW+\lambda (W^2-1)$
, so
$X=aW+\lambda (W^2-1)$
, so
![]() $\sigma (X)^2=a^2+2\lambda ^2$
. Suppose that
$\sigma (X)^2=a^2+2\lambda ^2$
. Suppose that
-
1.
 $\lambda \ge 0$
, or
$\lambda \ge 0$
, or -
2.
 $\sigma (X)\ge 10A'\cdot |\lambda |$
.
$\sigma (X)\ge 10A'\cdot |\lambda |$
.
Then for any
![]() $0\le u\le A'\sigma (X)$
, we have
$0\le u\le A'\sigma (X)$
, we have
![]() $p_X(u)\gtrsim _{A'} 1/{\sigma (X)}$
.
$p_X(u)\gtrsim _{A'} 1/{\sigma (X)}$
.
Proof. We may assume
![]() $a\ge 0$
(changing a to
$a\ge 0$
(changing a to
![]() $-a$
does not change the distribution of X). First, note that the case
$-a$
does not change the distribution of X). First, note that the case
![]() $\lambda =0$
is easy since then we have
$\lambda =0$
is easy since then we have
![]() $\sigma (X)=a$
and
$\sigma (X)=a$
and
![]() $p_X(u)=e^{-(u/a)^2/2}/(\sqrt {2\pi }a)\gtrsim _{A'} 1/\sigma (X)$
. So let us assume
$p_X(u)=e^{-(u/a)^2/2}/(\sqrt {2\pi }a)\gtrsim _{A'} 1/\sigma (X)$
. So let us assume
![]() $\lambda \neq 0$
and define
$\lambda \neq 0$
and define
![]() $g\colon \mathbb {R}\to \mathbb {R}$
by
$g\colon \mathbb {R}\to \mathbb {R}$
by
Then for all
![]() $t\in \mathbb {R}$
, we have
$t\in \mathbb {R}$
, we have
Hence, for any
![]() $t\in \mathbb {R}$
with
$t\in \mathbb {R}$
with
![]() $g(t)=u$
, recalling
$g(t)=u$
, recalling
![]() $0\le u\le A'\sigma (X)$
, we obtain
$0\le u\le A'\sigma (X)$
, we obtain
![]() $|g'(t)|\leq \sqrt {4(A'+1)\sigma (X)^2}\lesssim _{A'} \sigma (X)$
.
$|g'(t)|\leq \sqrt {4(A'+1)\sigma (X)^2}\lesssim _{A'} \sigma (X)$
.
We claim that we can find
![]() $t\in [-3A',3A']$
with
$t\in [-3A',3A']$
with
![]() $g(t)=u$
. Indeed, in case (1), we have
$g(t)=u$
. Indeed, in case (1), we have
![]() $g(0)=-\lambda \leq u$
and
$g(0)=-\lambda \leq u$
and
![]() $g(2A'+1)\geq 2A'a+2A'\lambda \geq A'\sigma (X)\geq u$
, and hence by the intermediate value theorem there exists
$g(2A'+1)\geq 2A'a+2A'\lambda \geq A'\sigma (X)\geq u$
, and hence by the intermediate value theorem there exists
![]() $t\in [0,2A'+1]\subseteq [-3A',3A']$
with
$t\in [0,2A'+1]\subseteq [-3A',3A']$
with
![]() $g(t)=u$
. In case (2), observe that
$g(t)=u$
. In case (2), observe that
![]() $a^2=\sigma (X)^2-2\lambda ^2\geq 100 A^{\prime 2}\cdot \lambda ^2-2\lambda ^2\geq 81A^{\prime 2}\cdot \lambda ^2$
, so
$a^2=\sigma (X)^2-2\lambda ^2\geq 100 A^{\prime 2}\cdot \lambda ^2-2\lambda ^2\geq 81A^{\prime 2}\cdot \lambda ^2$
, so
![]() $a\geq 9A'\cdot |\lambda |$
and therefore
$a\geq 9A'\cdot |\lambda |$
and therefore
![]() $|\lambda (9A^{\prime 2}-1)|\leq A'a$
and
$|\lambda (9A^{\prime 2}-1)|\leq A'a$
and
![]() $\sigma (X)^2=a^2+2\lambda ^2\leq 4a^2$
. Hence,
$\sigma (X)^2=a^2+2\lambda ^2\leq 4a^2$
. Hence,
![]() $g(-3A')=-3A'a+\lambda (9A^{\prime 2}-1)\leq -2A'a\leq 0\leq u$
and
$g(-3A')=-3A'a+\lambda (9A^{\prime 2}-1)\leq -2A'a\leq 0\leq u$
and
![]() $g(3A')=3A'a+\lambda (9A^{\prime 2}-1)\geq 2A'a\geq A'\sigma (X)\geq u$
and we can again conclude that there exists
$g(3A')=3A'a+\lambda (9A^{\prime 2}-1)\geq 2A'a\geq A'\sigma (X)\geq u$
and we can again conclude that there exists
![]() $t\in [-3A',3A']$
with
$t\in [-3A',3A']$
with
![]() $g(t)=u$
.
$g(t)=u$
.
Now, we have
 $$\begin{align*}p_X(u)=p_{g(W)}(g(t))\geq \frac{p_W(t)}{|g'(t)|}\gtrsim_{A'} \frac{e^{-(3A')^2/2}}{\sigma(X)}\gtrsim_{A'} \frac{1}{\sigma(X)}.\\[-42pt] \end{align*}$$
$$\begin{align*}p_X(u)=p_{g(W)}(g(t))\geq \frac{p_W(t)}{|g'(t)|}\gtrsim_{A'} \frac{e^{-(3A')^2/2}}{\sigma(X)}\gtrsim_{A'} \frac{1}{\sigma(X)}.\\[-42pt] \end{align*}$$
We need one more ingredient for the proof of Theorem 5.2(2): A variant of the Paley–Zygmund inequality which tells us that under a fourth-moment condition, random variables are reasonably likely to have small fluctuations in a given direction. We include a short proof; the result can also easily be deduced from [Reference Alon, Gutin and Krivelevich5, Lemma 3.2(i)].
Lemma 5.9. Fix
![]() $B\ge 1$
. If X is a real random variable with
$B\ge 1$
. If X is a real random variable with
![]() $\mathbb {E}[X] = 0$
and
$\mathbb {E}[X] = 0$
and
![]() $\sigma (X)>0$
satisfying
$\sigma (X)>0$
satisfying
![]() $\mathbb {E}[X^4]\le B\sigma (X)^4$
, then
$\mathbb {E}[X^4]\le B\sigma (X)^4$
, then
Proof. By rescaling, we may assume that
![]() $\sigma (X) = 1$
. Note that then
$\sigma (X) = 1$
. Note that then

where we have used that
for all
![]() $x\in \mathbb {R}$
. The result follows.
$x\in \mathbb {R}$
. The result follows.
Now, we prove Theorem 5.2(2).
Proof of Theorem 5.2(2)
We may assume
![]() $\sigma (f)=1$
. Borrowing the notation from the proof of Theorem 1.6, we write
$\sigma (f)=1$
. Borrowing the notation from the proof of Theorem 1.6, we write
 $$\begin{align*}f-\mathbb E f= \sum_{i=1}^n(a_iW_i+\lambda_i(W_i^2-1)), \end{align*}$$
$$\begin{align*}f-\mathbb E f= \sum_{i=1}^n(a_iW_i+\lambda_i(W_i^2-1)), \end{align*}$$
with
![]() $(W_1,\ldots ,W_n)\sim \mathcal {N}(0,1)^{\otimes n}$
, and
$(W_1,\ldots ,W_n)\sim \mathcal {N}(0,1)^{\otimes n}$
, and
![]() $\sigma _i^2=a_i^2+2\lambda _i^2$
(then we have
$\sigma _i^2=a_i^2+2\lambda _i^2$
(then we have
![]() $1=\sigma ^2=\sigma _1^2+\cdots +\sigma _n^2$
). It now suffices to prove that for all
$1=\sigma ^2=\sigma _1^2+\cdots +\sigma _n^2$
). It now suffices to prove that for all
![]() $u\in [0,A+1]$
we have
$u\in [0,A+1]$
we have
![]() $p_{f-\mathbb E f}(u) \gtrsim _A 1$
. Let L be a large integer depending only on A (such that
$p_{f-\mathbb E f}(u) \gtrsim _A 1$
. Let L be a large integer depending only on A (such that
![]() $L\geq 2$
and
$L\geq 2$
and
![]() $L\geq C_{5.5}(1+32C_{5.5}')\cdot 2\sqrt {2\pi }\cdot e^{(A+1)^2/2}$
for the constants
$L\geq C_{5.5}(1+32C_{5.5}')\cdot 2\sqrt {2\pi }\cdot e^{(A+1)^2/2}$
for the constants
![]() $C_{5.5}$
and
$C_{5.5}$
and
![]() $C_{5.5}'$
in Lemma 5.5). We break into cases.
$C_{5.5}'$
in Lemma 5.5). We break into cases.
First, suppose
![]() $\max _i\sigma _i\le 1/L$
. In this case, we define
$\max _i\sigma _i\le 1/L$
. In this case, we define
![]() $\Gamma =\sigma (f)^{3}/\sum _{i=1}^n\sigma _i^3=1/\sum _{i=1}^n\sigma _i^3$
and note that
$\Gamma =\sigma (f)^{3}/\sum _{i=1}^n\sigma _i^3=1/\sum _{i=1}^n\sigma _i^3$
and note that
![]() $\sum _{i=1}^{n}\sigma _i^3\le (\max _i\sigma _i)(\sum _{i=1}^{n} \sigma _i^2)\le 1/L$
, so
$\sum _{i=1}^{n}\sigma _i^3\le (\max _i\sigma _i)(\sum _{i=1}^{n} \sigma _i^2)\le 1/L$
, so
![]() $\Gamma \ge L$
. We also have
$\Gamma \ge L$
. We also have
![]() $\sigma _i^2\leq 1/L^2\leq 1/4$
, so Lemma 5.5(b) applies. So by combining parts (a) and (b) of Lemma 5.5, for all
$\sigma _i^2\leq 1/L^2\leq 1/4$
, so Lemma 5.5(b) applies. So by combining parts (a) and (b) of Lemma 5.5, for all
![]() $u\in [0,A+1]$
we obtain, as desired,
$u\in [0,A+1]$
we obtain, as desired,
 $$\begin{align*}p_{f-\mathbb E f}(u)\ge \frac{e^{-u^2/2}}{\sqrt{2\pi}}-\frac{C_{5.5}(1+32C_{5.5}')}{\Gamma}\ge \frac{e^{-(A+1)^2/2}}{\sqrt{2\pi}}-\frac{C_{5.5}(1+32C_{5.5}')}{L}\ge \frac12\cdot \frac{e^{-(A+1)^2/2}}{\sqrt{2\pi}}\gtrsim_A 1.\end{align*}$$
$$\begin{align*}p_{f-\mathbb E f}(u)\ge \frac{e^{-u^2/2}}{\sqrt{2\pi}}-\frac{C_{5.5}(1+32C_{5.5}')}{\Gamma}\ge \frac{e^{-(A+1)^2/2}}{\sqrt{2\pi}}-\frac{C_{5.5}(1+32C_{5.5}')}{L}\ge \frac12\cdot \frac{e^{-(A+1)^2/2}}{\sqrt{2\pi}}\gtrsim_A 1.\end{align*}$$
Otherwise, there is
![]() $i^*\in [n]$
such that
$i^*\in [n]$
such that
![]() $\sigma _{i^*} \ge 1/L$
. We claim that then there is an index
$\sigma _{i^*} \ge 1/L$
. We claim that then there is an index
![]() $j\in [n]$
satisfying at least one of the following two conditions:
$j\in [n]$
satisfying at least one of the following two conditions:
-
(1)
 $\sigma _{j} \ge 1/(10(A+19)L^2)$
and
$\sigma _{j} \ge 1/(10(A+19)L^2)$
and
 $\lambda _{j}\geq 0$
, or
$\lambda _{j}\geq 0$
, or -
(2)
 $\sigma _{j} \ge 1/L$
and
$\sigma _{j} \ge 1/L$
and
 $10(A+19)L\cdot |\lambda _{j}|\le \sigma _{j}$
.
$10(A+19)L\cdot |\lambda _{j}|\le \sigma _{j}$
.
Indeed, if
![]() $10(A+19)L\cdot |\lambda _{i^*}|\le \sigma _{i^*}$
we can simply take
$10(A+19)L\cdot |\lambda _{i^*}|\le \sigma _{i^*}$
we can simply take
![]() $j=i^*$
and (2) is satisfied. Otherwise, we have
$j=i^*$
and (2) is satisfied. Otherwise, we have
![]() $|\lambda _{i^*}|> \sigma _{i^*}/(10(A+19)L)\geq 1/(10(A+19)L^2)$
and the assumption in Theorem 5.2(2) yields
$|\lambda _{i^*}|> \sigma _{i^*}/(10(A+19)L)\geq 1/(10(A+19)L^2)$
and the assumption in Theorem 5.2(2) yields
![]() $\lambda _1\geq |\lambda _{i^*}|\geq 1/(10(A+19)L^2)$
. So in particular
$\lambda _1\geq |\lambda _{i^*}|\geq 1/(10(A+19)L^2)$
. So in particular
![]() $\lambda _1\geq 0$
and
$\lambda _1\geq 0$
and
![]() $\sigma _1\geq \lambda _1\geq 1/(10(A+19)L^2)$
, and we can take
$\sigma _1\geq \lambda _1\geq 1/(10(A+19)L^2)$
, and we can take
![]() $j=1$
and (1) is satisfied.
$j=1$
and (1) is satisfied.
Now, let
![]() $X_j=a_{j} W_{j}+\lambda _{j}(W_{j}^2-1)$
and let
$X_j=a_{j} W_{j}+\lambda _{j}(W_{j}^2-1)$
and let
![]() $X'=f-\mathbb E f-X_j=\sum _{i\neq j} (a_i W_i+\lambda _i(W_i^2-1))$
contain all terms of
$X'=f-\mathbb E f-X_j=\sum _{i\neq j} (a_i W_i+\lambda _i(W_i^2-1))$
contain all terms of
![]() $f-\mathbb E f$
except the term
$f-\mathbb E f$
except the term
![]() $X_j$
. By Theorem 4.14 (hypercontractivity), we have
$X_j$
. By Theorem 4.14 (hypercontractivity), we have
![]() $\mathbb E[(X')^4]\leq 81\sigma (X')^4$
, and therefore, Lemma 5.9 shows that
$\mathbb E[(X')^4]\leq 81\sigma (X')^4$
, and therefore, Lemma 5.9 shows that
![]() $-18\le -18\sigma (X')\le X'\le 0$
with probability at least
$-18\le -18\sigma (X')\le X'\le 0$
with probability at least
![]() $1/405$
.
$1/405$
.
We claim that we can apply Lemma 5.8 to
![]() $X_j$
and
$X_j$
and
![]() $u\in [0,A+19]$
, showing that
$u\in [0,A+19]$
, showing that
![]() $p_{X_j}(u)\gtrsim _A 1/\sigma _{j}\geq 1$
. Indeed, in case (1) we have
$p_{X_j}(u)\gtrsim _A 1/\sigma _{j}\geq 1$
. Indeed, in case (1) we have
![]() $0\leq u\leq 10(A+19)^2L^2\sigma _j$
and can apply case (1) of Lemma 5.8 with
$0\leq u\leq 10(A+19)^2L^2\sigma _j$
and can apply case (1) of Lemma 5.8 with
![]() $A'=10(A+19)^2L^2$
, while in case (2) we have
$A'=10(A+19)^2L^2$
, while in case (2) we have
![]() $0\leq u\leq (A+19)L\sigma _j$
and can apply case (2) of Lemma 5.8 with
$0\leq u\leq (A+19)L\sigma _j$
and can apply case (2) of Lemma 5.8 with
![]() $A'=(A+19)L$
.
$A'=(A+19)L$
.
Therefore, for any
![]() $u\in [0,A+1]$
we obtain
$u\in [0,A+1]$
we obtain
 $$ \begin{align*} p_{f-\mathbb E f}(u)=p_{X'+X_j}(u)&\geq \int_{-18}^{0} p_{X'}(y)p_{X_j}(u-y)\,dy\\ &\gtrsim_A \int_{-18}^{0} p_{X'}(y)\,dy =\Pr[-18\leq X'\leq 0]\gtrsim 1.\\[-45pt] \end{align*} $$
$$ \begin{align*} p_{f-\mathbb E f}(u)=p_{X'+X_j}(u)&\geq \int_{-18}^{0} p_{X'}(y)p_{X_j}(u-y)\,dy\\ &\gtrsim_A \int_{-18}^{0} p_{X'}(y)\,dy =\Pr[-18\leq X'\leq 0]\gtrsim 1.\\[-45pt] \end{align*} $$
5.4 Nonuniform anticoncentration
In this subsection, we prove Theorem 5.2(1), which is essentially a nonuniform version of Theorem 1.6. We begin with a lemma giving nonuniform anticoncentration bounds for a quadratic polynomial of a single Gaussian variable, that is, for one of the terms in our sum.
Lemma 5.10. Let
![]() $W\sim \mathcal N(0,1)$
and for some
$W\sim \mathcal N(0,1)$
and for some
![]() $a,\lambda \in \mathbb {R}$
(not both zero) let
$a,\lambda \in \mathbb {R}$
(not both zero) let
![]() $X=aW+\lambda (W^2-1)$
, so
$X=aW+\lambda (W^2-1)$
, so
![]() $\sigma ^2:=\sigma (X)^2=a^2+2\lambda ^2$
. Suppose we are given some
$\sigma ^2:=\sigma (X)^2=a^2+2\lambda ^2$
. Suppose we are given some
![]() $x\geq 10^3\sigma $
satisfying
$x\geq 10^3\sigma $
satisfying
![]() $|\lambda |\cdot x\leq a^2/10$
. Then for each
$|\lambda |\cdot x\leq a^2/10$
. Then for each
![]() $u\in \mathbb {R}$
with
$u\in \mathbb {R}$
with
![]() $x/10\leq |u|\leq 2x$
, we have
$x/10\leq |u|\leq 2x$
, we have
Proof. Define the function
![]() $g\colon \mathbb {R}\to \mathbb {R}$
by
$g\colon \mathbb {R}\to \mathbb {R}$
by
![]() $g(t)=at+\lambda (t^2-1)$
. As in the proof of Lemma 5.8, we can calculate
$g(t)=at+\lambda (t^2-1)$
. As in the proof of Lemma 5.8, we can calculate
![]() $(g'(t))^2=4\lambda \cdot g(t)+4\lambda ^2+a^2$
for all
$(g'(t))^2=4\lambda \cdot g(t)+4\lambda ^2+a^2$
for all
![]() $t\in \mathbb {R}$
. Now, consider some
$t\in \mathbb {R}$
. Now, consider some
![]() $u\in \mathbb {R}$
with
$u\in \mathbb {R}$
with
![]() $x/10\leq |u|\leq 2x$
. There are at most two different
$x/10\leq |u|\leq 2x$
. There are at most two different
![]() $t\in \mathbb {R}$
with
$t\in \mathbb {R}$
with
![]() $g(t)=u$
. For any such t, we have (using the assumption that
$g(t)=u$
. For any such t, we have (using the assumption that
![]() $|\lambda |\cdot x\leq a^2/10$
)
$|\lambda |\cdot x\leq a^2/10$
)
We furthermore claim that any such t must satisfy
![]() $|t|\geq x/(20|a|)$
. Indeed, if
$|t|\geq x/(20|a|)$
. Indeed, if
![]() $|t|< x/(20|a|)$
, then (using that
$|t|< x/(20|a|)$
, then (using that
![]() $x\geq 10^3\sigma \geq 10^3a$
and the assumption
$x\geq 10^3\sigma \geq 10^3a$
and the assumption
![]() $|\lambda |\cdot x\leq a^2/10$
)
$|\lambda |\cdot x\leq a^2/10$
)
 $$\begin{align*}|g(t)|=|at+\lambda(t^2-1)|\leq |a|\cdot \frac{x}{20|a|}+|\lambda|\cdot \max\left\{\frac{x^2}{400a^2},1\right\}\leq \frac{x}{20}+|\lambda|\cdot\frac{x^2}{400a^2}\leq \frac{x}{20}+\frac{x}{4000}<\frac{x}{10}.\end{align*}$$
$$\begin{align*}|g(t)|=|at+\lambda(t^2-1)|\leq |a|\cdot \frac{x}{20|a|}+|\lambda|\cdot \max\left\{\frac{x^2}{400a^2},1\right\}\leq \frac{x}{20}+|\lambda|\cdot\frac{x^2}{400a^2}\leq \frac{x}{20}+\frac{x}{4000}<\frac{x}{10}.\end{align*}$$
As
![]() $|u|\geq x/10$
, this contradicts
$|u|\geq x/10$
, this contradicts
![]() $g(t)=u$
. Thus, any
$g(t)=u$
. Thus, any
![]() $t\in \mathbb {R}$
with
$t\in \mathbb {R}$
with
![]() $g(t)=u$
must indeed also satisfy
$g(t)=u$
must indeed also satisfy
![]() $|t|\geq x/(20|a|)$
. Now, we obtain (using again that
$|t|\geq x/(20|a|)$
. Now, we obtain (using again that
![]() $x\geq 10^3\sigma \geq 10^3a$
)
$x\geq 10^3\sigma \geq 10^3a$
)
 $$\begin{align*}p_X(u)=\sum_{\substack{t\in\mathbb{R}\\g(t)=u}} \frac{p_W(t)}{|g'(t)|}\leq 2\cdot \frac{1}{|a|/3}\cdot \exp\left(-\frac{x^2}{800a^2}\right)\lesssim \frac{1}{|a|}\exp\left(-\frac{x}{\sigma}\right). \\[-55pt] \end{align*}$$
$$\begin{align*}p_X(u)=\sum_{\substack{t\in\mathbb{R}\\g(t)=u}} \frac{p_W(t)}{|g'(t)|}\leq 2\cdot \frac{1}{|a|/3}\cdot \exp\left(-\frac{x^2}{800a^2}\right)\lesssim \frac{1}{|a|}\exp\left(-\frac{x}{\sigma}\right). \\[-55pt] \end{align*}$$
Now, we prove Theorem 5.2(1). The main idea is to divide our random variable
![]() $f-\mathbb E f$
into independent parts, to take advantage of exponential tail bounds (by Theorem 4.15 or Lemma 5.10) for one of the parts, and anticoncentration bounds (by Theorem 1.6) for the rest of the parts.
$f-\mathbb E f$
into independent parts, to take advantage of exponential tail bounds (by Theorem 4.15 or Lemma 5.10) for one of the parts, and anticoncentration bounds (by Theorem 1.6) for the rest of the parts.
Proof of Theorem 5.2(1)
By rescaling, we may assume
![]() $\sigma :=\sigma (f)=1$
. If
$\sigma :=\sigma (f)=1$
. If
![]() $|x|\leq 10^3=10^3\sigma (f)$
, the desired bound follows from Theorem 1.6. So we may assume that
$|x|\leq 10^3=10^3\sigma (f)$
, the desired bound follows from Theorem 1.6. So we may assume that
![]() $|x|\geq 10^3\sigma (f)$
. Also, note that the assumption in Theorem 5.2(1) implies that
$|x|\geq 10^3\sigma (f)$
. Also, note that the assumption in Theorem 5.2(1) implies that
![]() $\eta \le 1$
. Borrowing the notation from the proof of Theorem 1.6, we write
$\eta \le 1$
. Borrowing the notation from the proof of Theorem 1.6, we write
 $$\begin{align*}f-\mathbb E f= \sum_{i=1}^n(a_iW_i+\lambda_i(W_i^2-1)), \end{align*}$$
$$\begin{align*}f-\mathbb E f= \sum_{i=1}^n(a_iW_i+\lambda_i(W_i^2-1)), \end{align*}$$
with
![]() $(W_1,\ldots ,W_n)\sim \mathcal N(0,1)^{\otimes n}$
and
$(W_1,\ldots ,W_n)\sim \mathcal N(0,1)^{\otimes n}$
and
![]() $\sigma _i^2=a_i^2+2\lambda _i^2$
(then we have
$\sigma _i^2=a_i^2+2\lambda _i^2$
(then we have
![]() $1=\sigma ^2=\sigma _1^2+\cdots +\sigma _n^2$
). We may assume that
$1=\sigma ^2=\sigma _1^2+\cdots +\sigma _n^2$
). We may assume that
![]() $|\lambda _1|\geq \cdots \geq |\lambda _n|$
. Note that using Theorem 4.13 the assumption in Theorem 5.2(1) implies that for every subset
$|\lambda _1|\geq \cdots \geq |\lambda _n|$
. Note that using Theorem 4.13 the assumption in Theorem 5.2(1) implies that for every subset
![]() $I\subseteq [n]$
of size
$I\subseteq [n]$
of size
![]() $|I|=n-3$
we have
$|I|=n-3$
we have
![]() $\sum _{i\in I}\lambda _i^2\geq \eta (\lambda _1^2+\cdots +\lambda _n^2)$
. In particular,
$\sum _{i\in I}\lambda _i^2\geq \eta (\lambda _1^2+\cdots +\lambda _n^2)$
. In particular,
![]() $\sum _{i=4}^{n}\lambda _i^2\geq \eta (\lambda _1^2+\cdots +\lambda _n^2)$
.
$\sum _{i=4}^{n}\lambda _i^2\geq \eta (\lambda _1^2+\cdots +\lambda _n^2)$
.
By adding at most three terms with
![]() $a_i=\lambda _i=0$
, we may assume that
$a_i=\lambda _i=0$
, we may assume that
![]() $n\equiv 1 \pmod {4}$
. For a subset
$n\equiv 1 \pmod {4}$
. For a subset
![]() $J\subseteq [n]$
, let
$J\subseteq [n]$
, let
![]() $X_{J}=\sum _{i\in J}(a_iW_i+\lambda _i(W_i^2-1))$
and
$X_{J}=\sum _{i\in J}(a_iW_i+\lambda _i(W_i^2-1))$
and
![]() $\sigma _{J}^{2}=\sum _{i\in J}\sigma _{i}^2=\sigma (X_{J})^2$
.
$\sigma _{J}^{2}=\sum _{i\in J}\sigma _{i}^2=\sigma (X_{J})^2$
.
Let
![]() $i^*\in [n]$
be chosen such that
$i^*\in [n]$
be chosen such that
![]() $\sigma _{i^*}^2$
is maximal, and define
$\sigma _{i^*}^2$
is maximal, and define
![]() $J_0=\{i^*\}$
. We claim that we can find a partition of
$J_0=\{i^*\}$
. We claim that we can find a partition of
![]() $[n]\setminus J_0=[n]\setminus \{i^*\}$
into four subsets
$[n]\setminus J_0=[n]\setminus \{i^*\}$
into four subsets
![]() $J_1,J_2,J_3,J_4$
satisfying the following conditions.
$J_1,J_2,J_3,J_4$
satisfying the following conditions.
-
(a) For
 $h=1,2,3,4$
, we have
$h=1,2,3,4$
, we have
 $\sigma _{[n]\setminus J_h}^2\geq \eta /2$
.
$\sigma _{[n]\setminus J_h}^2\geq \eta /2$
. -
(b) For any
 $h=0,\ldots ,4$
and any subset
$h=0,\ldots ,4$
and any subset
 $I\subseteq [n]\setminus J_h$
of size
$I\subseteq [n]\setminus J_h$
of size
 $|I|=n-|J_h|-2$
, we have
$|I|=n-|J_h|-2$
, we have
 $\sum _{i\in I}\lambda _i^2\geq (\eta /4)\cdot (\lambda _1^2+\cdots +\lambda _n^2)$
.
$\sum _{i\in I}\lambda _i^2\geq (\eta /4)\cdot (\lambda _1^2+\cdots +\lambda _n^2)$
.
Indeed, we can build such a partition iteratively: Let us divide
![]() $[n]\setminus \{i^*\}$
into
$[n]\setminus \{i^*\}$
into
![]() $n/4$
quadruplets (starting with the four smallest indices, then the next four, and so on). Iteratively, for each quadruplet, distribute one element to each of
$n/4$
quadruplets (starting with the four smallest indices, then the next four, and so on). Iteratively, for each quadruplet, distribute one element to each of
![]() $J_1,J_2,J_3,J_4$
in the following way. We assign the index i in the quadruplet with the largest
$J_1,J_2,J_3,J_4$
in the following way. We assign the index i in the quadruplet with the largest
![]() $\sigma _i^2$
to the set
$\sigma _i^2$
to the set
![]() $J_h$
which had the smallest value of
$J_h$
which had the smallest value of
![]() $\sigma _{J_h}^{2}$
at the end of the last step, we assign the index i with the second-largest
$\sigma _{J_h}^{2}$
at the end of the last step, we assign the index i with the second-largest
![]() $\sigma _i^2$
to the set
$\sigma _i^2$
to the set
![]() $J_h$
which had the second-smallest value of
$J_h$
which had the second-smallest value of
![]() $\sigma _{J_h}^{2}$
, and so on. One can check that this assignment process maintains the property that at the end of any step, the values
$\sigma _{J_h}^{2}$
, and so on. One can check that this assignment process maintains the property that at the end of any step, the values
![]() $\sigma _{J_h}^{2}$
for
$\sigma _{J_h}^{2}$
for
![]() $h=1,2,3,4$
differ by at most
$h=1,2,3,4$
differ by at most
![]() $\max _{i}\sigma _{i}^{2}=\sigma _{i^*}^2$
. Hence,
$\max _{i}\sigma _{i}^{2}=\sigma _{i^*}^2$
. Hence,
![]() $\sigma _{[n]\setminus J_1}^2\geq \sigma _{J_2}^2+\sigma _{i^*}^2\geq \sigma _{J_1}^2=1-\sigma _{[n]\setminus J_1}^2$
, so
$\sigma _{[n]\setminus J_1}^2\geq \sigma _{J_2}^2+\sigma _{i^*}^2\geq \sigma _{J_1}^2=1-\sigma _{[n]\setminus J_1}^2$
, so
![]() $\sigma _{[n]\setminus J_1}^2\geq 1/2\geq \eta /2$
. Analogously, one can show
$\sigma _{[n]\setminus J_1}^2\geq 1/2\geq \eta /2$
. Analogously, one can show
![]() $\sigma _{[n]\setminus J_h}^2\geq \eta /2$
for
$\sigma _{[n]\setminus J_h}^2\geq \eta /2$
for
![]() $h=2,3,4$
, so (a) is satisfied. To check (b), note that for each
$h=2,3,4$
, so (a) is satisfied. To check (b), note that for each
![]() $h=0,\ldots ,4$
the set
$h=0,\ldots ,4$
the set
![]() $[n]\setminus J_h$
is missing either one element from each of the quadruplets considered during the construction (if
$[n]\setminus J_h$
is missing either one element from each of the quadruplets considered during the construction (if
![]() $1\leq h\leq 4$
) or is missing one element in total (if
$1\leq h\leq 4$
) or is missing one element in total (if
![]() $h=0$
). For a subset
$h=0$
). For a subset
![]() $I\subseteq [n]\setminus J_h$
of size
$I\subseteq [n]\setminus J_h$
of size
![]() $|I|=n-|J_h|-2$
, two additional elements are missing. Thus, for every
$|I|=n-|J_h|-2$
, two additional elements are missing. Thus, for every
![]() $k=1,\ldots ,n/4$
the set
$k=1,\ldots ,n/4$
the set
![]() $I\subseteq [n]$
is missing at most
$I\subseteq [n]$
is missing at most
![]() $k+2$
of the elements in
$k+2$
of the elements in
![]() $[4k]$
. Thus, recalling that
$[4k]$
. Thus, recalling that
![]() $|\lambda _1|\geq \cdots \geq |\lambda _n|$
, we obtain
$|\lambda _1|\geq \cdots \geq |\lambda _n|$
, we obtain
 $$ \begin{align*} \sum_{i\in I}\lambda_i^2 &\ge \lambda_4^2+(\lambda_6^2+\lambda_7^2+\lambda_8^2)+(\lambda_{10}^2+\lambda_{11}^2+\lambda_{12}^2)+\cdots \\[-2pt] &\geq \lambda_4^2+\lambda_8^2+\lambda_{12}^2+\cdots\ge \frac{1}{4}\sum_{i=4}^{n}\lambda_i^2\geq (\eta/4)\cdot (\lambda_1^2+\cdots+\lambda_n^2). \end{align*} $$
$$ \begin{align*} \sum_{i\in I}\lambda_i^2 &\ge \lambda_4^2+(\lambda_6^2+\lambda_7^2+\lambda_8^2)+(\lambda_{10}^2+\lambda_{11}^2+\lambda_{12}^2)+\cdots \\[-2pt] &\geq \lambda_4^2+\lambda_8^2+\lambda_{12}^2+\cdots\ge \frac{1}{4}\sum_{i=4}^{n}\lambda_i^2\geq (\eta/4)\cdot (\lambda_1^2+\cdots+\lambda_n^2). \end{align*} $$
This establishes (b). Thus, the sets
![]() $J_1,\ldots ,J_4$
indeed satisfy the desired conditions.
$J_1,\ldots ,J_4$
indeed satisfy the desired conditions.
By our assumption
![]() $|x|\geq 10^3\sigma (f)$
and by
$|x|\geq 10^3\sigma (f)$
and by
![]() $0\leq \varepsilon \leq \sigma (f)$
, we have
$0\leq \varepsilon \leq \sigma (f)$
, we have
![]() $|y|\geq 0.999|x|\geq (5/6)\cdot |x|$
for all
$|y|\geq 0.999|x|\geq (5/6)\cdot |x|$
for all
![]() $y\in [x,x+\varepsilon ]$
. Thus, whenever
$y\in [x,x+\varepsilon ]$
. Thus, whenever
![]() $f-\mathbb {E} f=\sum _{i=1}^n (a_iW_i+\lambda _i(W_i^2-1))=X_{J_0}+\cdots +X_{J_4}$
is contained in the interval
$f-\mathbb {E} f=\sum _{i=1}^n (a_iW_i+\lambda _i(W_i^2-1))=X_{J_0}+\cdots +X_{J_4}$
is contained in the interval
![]() $[x,x+\varepsilon ]$
, we must have
$[x,x+\varepsilon ]$
, we must have
![]() $|X_{J_h}|\geq |x|/6$
for at least one
$|X_{J_h}|\geq |x|/6$
for at least one
![]() $h\in \{0,\ldots ,4\}$
. So, we have
$h\in \{0,\ldots ,4\}$
. So, we have
 $$ \begin{align} \Pr[f-\mathbb{E} f\in [x,x+\varepsilon]] \leq \sum_{h=0}^{4}\Pr\Big[|X_{J_h}|\geq |x|/6\text{ and }X_{[n]\setminus J_h}\in [x-X_{J_h},x-X_{J_h}+\varepsilon]\Big]. \end{align} $$
$$ \begin{align} \Pr[f-\mathbb{E} f\in [x,x+\varepsilon]] \leq \sum_{h=0}^{4}\Pr\Big[|X_{J_h}|\geq |x|/6\text{ and }X_{[n]\setminus J_h}\in [x-X_{J_h},x-X_{J_h}+\varepsilon]\Big]. \end{align} $$
For
![]() $h= 1,\ldots ,4$
, note that
$h= 1,\ldots ,4$
, note that
 $$ \begin{align} &\Pr\Big[|X_{J_h}|\geq |x|/6\text{ and }X_{[n]\setminus J_h}\in [x-X_{J_h},x-X_{J_h}+\varepsilon]\Big]\notag\\ &\quad\le \Pr[|X_{J_h}|\ge|x|/6]\cdot \mathcal L(X_{[n]\setminus J_h},\varepsilon)\lesssim_{\eta} \exp\left(-\frac{2}{2e}\cdot \frac{|x|}{6\sigma_{J_h}}\right)\frac{\varepsilon}{\sigma_{[n]\setminus J_h}} \lesssim_{\eta}\frac{\varepsilon}{\sigma}\exp\left(-\Omega\left(\frac{|x|}{\sigma}\right)\right), \end{align} $$
$$ \begin{align} &\Pr\Big[|X_{J_h}|\geq |x|/6\text{ and }X_{[n]\setminus J_h}\in [x-X_{J_h},x-X_{J_h}+\varepsilon]\Big]\notag\\ &\quad\le \Pr[|X_{J_h}|\ge|x|/6]\cdot \mathcal L(X_{[n]\setminus J_h},\varepsilon)\lesssim_{\eta} \exp\left(-\frac{2}{2e}\cdot \frac{|x|}{6\sigma_{J_h}}\right)\frac{\varepsilon}{\sigma_{[n]\setminus J_h}} \lesssim_{\eta}\frac{\varepsilon}{\sigma}\exp\left(-\Omega\left(\frac{|x|}{\sigma}\right)\right), \end{align} $$
where in the second step we applied Theorem 4.15 to
![]() $X_{J_h}$
with
$X_{J_h}$
with
![]() $t=|x|/(6\sigma _{J_h})\geq |x|/(6\sigma )$
and Theorem 1.6 to
$t=|x|/(6\sigma _{J_h})\geq |x|/(6\sigma )$
and Theorem 1.6 to
![]() $X_{[n]\setminus J_h}$
(noting that the assumption of Theorem 1.6 is satisfied by condition (b); see also Remark 5.1), and in the last step we used that
$X_{[n]\setminus J_h}$
(noting that the assumption of Theorem 1.6 is satisfied by condition (b); see also Remark 5.1), and in the last step we used that
![]() $\sigma _{[n]\setminus J_h}^2\geq \eta /2$
by condition (a).
$\sigma _{[n]\setminus J_h}^2\geq \eta /2$
by condition (a).
We now distinguish two cases. First, let us assume that
![]() $\sigma _{[n]\setminus J_0}\ge \eta ^2/(100|x|)$
. In this case, similarly to (5.3), we can bound (recalling that
$\sigma _{[n]\setminus J_0}\ge \eta ^2/(100|x|)$
. In this case, similarly to (5.3), we can bound (recalling that
![]() $\sigma =1$
)
$\sigma =1$
)
 $$ \begin{align*} &\Pr\Big[|X_{J_0}|\geq |x|/6\text{ and }X_{[n]\setminus J_0}\in [x-X_{J_0},x-X_{J_0}+\varepsilon]\Big]\\ &\qquad\lesssim_{\eta} \exp\left(-\frac{2}{2e}\cdot \frac{|x|}{6\sigma_{J_0}}\right)\cdot \frac{\varepsilon}{\sigma_{[n]\setminus J_0}} \lesssim_{\eta}\frac{\varepsilon}{\sigma}\cdot \frac{|x|}{40\sigma}\cdot \exp\left(-\frac{|x|}{20\sigma}\right)\le \frac{\varepsilon}{\sigma}\exp\left(-\frac{|x|}{40\sigma}\right), \end{align*} $$
$$ \begin{align*} &\Pr\Big[|X_{J_0}|\geq |x|/6\text{ and }X_{[n]\setminus J_0}\in [x-X_{J_0},x-X_{J_0}+\varepsilon]\Big]\\ &\qquad\lesssim_{\eta} \exp\left(-\frac{2}{2e}\cdot \frac{|x|}{6\sigma_{J_0}}\right)\cdot \frac{\varepsilon}{\sigma_{[n]\setminus J_0}} \lesssim_{\eta}\frac{\varepsilon}{\sigma}\cdot \frac{|x|}{40\sigma}\cdot \exp\left(-\frac{|x|}{20\sigma}\right)\le \frac{\varepsilon}{\sigma}\exp\left(-\frac{|x|}{40\sigma}\right), \end{align*} $$
where in the last step we used that
![]() $te^{-t}\le 1/e\le 1$
for all
$te^{-t}\le 1/e\le 1$
for all
![]() $t\in \mathbb {R}$
(specifically, we used this for
$t\in \mathbb {R}$
(specifically, we used this for
![]() $t=|x|/(40\sigma )$
). Together with (5.3), this enables us to bound all five summands on the right-hand side of (5.2), implying the desired bound for
$t=|x|/(40\sigma )$
). Together with (5.3), this enables us to bound all five summands on the right-hand side of (5.2), implying the desired bound for
![]() $\Pr [f-\mathbb {E} f\in [x,x+\varepsilon ]]$
.
$\Pr [f-\mathbb {E} f\in [x,x+\varepsilon ]]$
.
It remains to consider the case that
![]() $\sigma _{[n]\setminus J_0}< \eta ^2/(100|x|)$
. Then we in particular have
$\sigma _{[n]\setminus J_0}< \eta ^2/(100|x|)$
. Then we in particular have
![]() $\sigma _{i^*}^2=1-\sigma _{[n]\setminus J_0}^2\ge 1-\eta ^4/(10^4|x|^2)\ge 1-\eta /2$
. Furthermore, the assumption in Theorem 5.2(1) implies
$\sigma _{i^*}^2=1-\sigma _{[n]\setminus J_0}^2\ge 1-\eta ^4/(10^4|x|^2)\ge 1-\eta /2$
. Furthermore, the assumption in Theorem 5.2(1) implies
![]() $\sum _{i\in [n]\setminus \{i^*\}} \lambda _i^2\geq \eta (\lambda _1^2+\cdots +\lambda _n^2)$
, and therefore
$\sum _{i\in [n]\setminus \{i^*\}} \lambda _i^2\geq \eta (\lambda _1^2+\cdots +\lambda _n^2)$
, and therefore
![]() $\lambda _{i^*}^2\leq (1-\eta )(\lambda _1^2+\cdots +\lambda _n^2)\leq (1-\eta )/2$
(recalling that
$\lambda _{i^*}^2\leq (1-\eta )(\lambda _1^2+\cdots +\lambda _n^2)\leq (1-\eta )/2$
(recalling that
![]() $1=\sigma ^2=\sum _{i=1}^{n}(a_i^2+2\lambda _i^2)$
). Thus, we obtain
$1=\sigma ^2=\sum _{i=1}^{n}(a_i^2+2\lambda _i^2)$
). Thus, we obtain
![]() $a_{i^*}^2=\sigma _{i^*}^2-2\lambda _{i^*}^2\geq (1-\eta /2)-(1-\eta )= \eta /2$
. Our assumption also implies
$a_{i^*}^2=\sigma _{i^*}^2-2\lambda _{i^*}^2\geq (1-\eta /2)-(1-\eta )= \eta /2$
. Our assumption also implies
![]() $\eta ^4/(10^4|x|^2)> \sigma _{[n]\setminus J_0}^2 \ge \sum _{i\in [n]\setminus \{i^*\}} \lambda _i^2 \ge \eta \lambda _{i*}^2$
, meaning that
$\eta ^4/(10^4|x|^2)> \sigma _{[n]\setminus J_0}^2 \ge \sum _{i\in [n]\setminus \{i^*\}} \lambda _i^2 \ge \eta \lambda _{i*}^2$
, meaning that
![]() $|\lambda _{i^*}|\cdot |x|\le \eta /100 \le a^2_{i^*}/10$
.
$|\lambda _{i^*}|\cdot |x|\le \eta /100 \le a^2_{i^*}/10$
.
Now, we observe
 $$ \begin{align*} &\Pr[f-\mathbb{E} f\in [x,x+\varepsilon]]\\ &\qquad \leq \sum_{h=1}^{4}\Pr\Big[|X_{J_h}|\geq |x|/6\text{ and }X_{[n]\setminus J_h}\in [x-X_{J_h},x-X_{J_h}+\varepsilon]\Big]\\ &\qquad\qquad\qquad+\Pr\Big[|X_{[n]\setminus J_0}|\leq (4/6)|x|\text{ and }X_{J_0}\in [x-X_{[n]\setminus J_0},x-X_{[n]\setminus J_0}+\varepsilon]\Big]. \end{align*} $$
$$ \begin{align*} &\Pr[f-\mathbb{E} f\in [x,x+\varepsilon]]\\ &\qquad \leq \sum_{h=1}^{4}\Pr\Big[|X_{J_h}|\geq |x|/6\text{ and }X_{[n]\setminus J_h}\in [x-X_{J_h},x-X_{J_h}+\varepsilon]\Big]\\ &\qquad\qquad\qquad+\Pr\Big[|X_{[n]\setminus J_0}|\leq (4/6)|x|\text{ and }X_{J_0}\in [x-X_{[n]\setminus J_0},x-X_{[n]\setminus J_0}+\varepsilon]\Big]. \end{align*} $$
Again, (5.3) gives an upper bound for the summands for
![]() $h=1,\ldots ,4$
. To bound the last summand, let us fix any outcome of
$h=1,\ldots ,4$
. To bound the last summand, let us fix any outcome of
![]() $X_{[n]\setminus J_0}$
with
$X_{[n]\setminus J_0}$
with
![]() $|X_{[n]\setminus J_0}|\leq (4/6)|x|$
. Then the probability that
$|X_{[n]\setminus J_0}|\leq (4/6)|x|$
. Then the probability that
![]() $X_{J_0}=a_{i^*}W_{i^*}+\lambda _{i^*}(W_{i^*}^2-1)$
lies in the interval
$X_{J_0}=a_{i^*}W_{i^*}+\lambda _{i^*}(W_{i^*}^2-1)$
lies in the interval
![]() $[x-X_{[n]\setminus J_0},x-X_{[n]\setminus J_0}+\varepsilon ]$
(which has length
$[x-X_{[n]\setminus J_0},x-X_{[n]\setminus J_0}+\varepsilon ]$
(which has length
![]() $\varepsilon $
and is somewhere between
$\varepsilon $
and is somewhere between
![]() $x/10$
and
$x/10$
and
![]() $2x$
) is by Lemma 5.10 bounded by
$2x$
) is by Lemma 5.10 bounded by
 $$\begin{align*}\Pr[X_{J_0}\in [x-X_{[n]\setminus J_0},x-X_{[n]\setminus J_0}+\varepsilon]]\lesssim \frac{\varepsilon}{|a_{i^*}|}\exp\left(-\frac{|x|}{\sigma_{J_0}}\right)\lesssim_{\eta} \frac{\varepsilon}{\sigma}\exp\left(-\frac{|x|}{\sigma}\right),\end{align*}$$
$$\begin{align*}\Pr[X_{J_0}\in [x-X_{[n]\setminus J_0},x-X_{[n]\setminus J_0}+\varepsilon]]\lesssim \frac{\varepsilon}{|a_{i^*}|}\exp\left(-\frac{|x|}{\sigma_{J_0}}\right)\lesssim_{\eta} \frac{\varepsilon}{\sigma}\exp\left(-\frac{|x|}{\sigma}\right),\end{align*}$$
where in the last step we used that
![]() $a_{i^*}^2\geq \eta /2$
(see above). Thus, we again obtain the desired bound for
$a_{i^*}^2\geq \eta /2$
(see above). Thus, we again obtain the desired bound for
![]() $\Pr [f-\mathbb {E} f\in [x,x+\varepsilon ]]$
.
$\Pr [f-\mathbb {E} f\in [x,x+\varepsilon ]]$
.
5.5 Control of Gaussian characteristic functions
For later, we also record the fact that under a robust rank assumption, characteristic functions of certain ‘quadratic’ functions of Gaussian random variables decay rapidly.
Lemma 5.11. Fix a positive integer r. Let
![]() $\vec Z = (Z_1,\ldots ,Z_n)\sim \mathcal {N}(0,1)^{\otimes n}$
be a vector of independent standard Gaussian random variables. Consider a real quadratic polynomial
$\vec Z = (Z_1,\ldots ,Z_n)\sim \mathcal {N}(0,1)^{\otimes n}$
be a vector of independent standard Gaussian random variables. Consider a real quadratic polynomial
![]() $f(\vec Z)$
of
$f(\vec Z)$
of
![]() $\vec Z$
, written as
$\vec Z$
, written as
for some symmetric matrix
![]() $F\in \mathbb {R}^{n\times n}$
, some vector
$F\in \mathbb {R}^{n\times n}$
, some vector
![]() $\vec f\in \mathbb {R}^n$
and some
$\vec f\in \mathbb {R}^n$
and some
![]() $f_0\in \mathbb {R}$
. Let
$f_0\in \mathbb {R}$
. Let
 $$\begin{align*}s=\min_{\substack{\widetilde F\in\,\mathbb{R}^{n\times n}\\\operatorname{rank} \widetilde F\le r}}\|F-\widetilde F\|_{\mathrm F}^2.\end{align*}$$
$$\begin{align*}s=\min_{\substack{\widetilde F\in\,\mathbb{R}^{n\times n}\\\operatorname{rank} \widetilde F\le r}}\|F-\widetilde F\|_{\mathrm F}^2.\end{align*}$$
Then for any
![]() $\tau \in \mathbb {R}$
, we have
$\tau \in \mathbb {R}$
, we have
Proof. Let
![]() $\lambda _1,\ldots ,\lambda _n$
be the eigenvalues of F, ordered such that
$\lambda _1,\ldots ,\lambda _n$
be the eigenvalues of F, ordered such that
![]() $|\lambda _1|\ge \cdots \ge |\lambda _n|$
. By Theorem 4.13, we have
$|\lambda _1|\ge \cdots \ge |\lambda _n|$
. By Theorem 4.13, we have
![]() $s=\sum _{j=r+1}^n\lambda _j^2$
.
$s=\sum _{j=r+1}^n\lambda _j^2$
.
As in the proof of Theorem 1.6, we write
![]() $f(\vec Z)-\mathbb {E}[f(\vec Z)]=\sum _{j=1}^{n}(a_jW_j + \lambda _i(W_j^2-1))$
, where
$f(\vec Z)-\mathbb {E}[f(\vec Z)]=\sum _{j=1}^{n}(a_jW_j + \lambda _i(W_j^2-1))$
, where
![]() $(W_1,\ldots ,W_n)\sim \mathcal {N}(0,1)^{\otimes n}$
are independent standard Gaussians. From Lemma 5.4, recall that
$(W_1,\ldots ,W_n)\sim \mathcal {N}(0,1)^{\otimes n}$
are independent standard Gaussians. From Lemma 5.4, recall that
 $$\begin{align*}|\mathbb{E}\exp(i\tau (a_j W_j+\lambda_j(W_j^2-1)))|=|\mathbb{E}\exp(i\tau (a_j W_j+\lambda_jW_j^2))| \le \frac{1}{(1+4\lambda_j^2\tau^2)^{1/4}}\end{align*}$$
$$\begin{align*}|\mathbb{E}\exp(i\tau (a_j W_j+\lambda_j(W_j^2-1)))|=|\mathbb{E}\exp(i\tau (a_j W_j+\lambda_jW_j^2))| \le \frac{1}{(1+4\lambda_j^2\tau^2)^{1/4}}\end{align*}$$
for
![]() $j=1,\ldots ,n$
. We then deduce
$j=1,\ldots ,n$
. We then deduce
 $$ \begin{align*} |\mathbb{E}[\exp(i\tau f(\vec{Z}))]| &= \prod_{j=1}^{n}|\mathbb{E}[\exp(i\tau (a_jW + \lambda_j(W_j^2-1)))]| \le \prod_{j=1}^{n}\frac{1}{(1+4\lambda_j^2\tau^2)^{1/4}}\\ &\le \prod_{j=1}^{r}\left(1+4\tau^2\sum_{t=0}^{\lfloor{(n-j)/r}\rfloor}\lambda_{j + rt}^2\right)^{-1/4}\le \left(1+4\tau^2\sum_{t=0}^{\lfloor{(n-r)/r}\rfloor}\lambda_{r+rt}^2\right)^{-r/4}\\ &\le \left(1+\frac{4\tau^2}r\sum_{j=r+1}^{n}\lambda_{j}^2\right)^{-r/4}\lesssim_{r} \frac{1}{(1+\tau^2s)^{r/4}}. \\[-48pt] \end{align*} $$
$$ \begin{align*} |\mathbb{E}[\exp(i\tau f(\vec{Z}))]| &= \prod_{j=1}^{n}|\mathbb{E}[\exp(i\tau (a_jW + \lambda_j(W_j^2-1)))]| \le \prod_{j=1}^{n}\frac{1}{(1+4\lambda_j^2\tau^2)^{1/4}}\\ &\le \prod_{j=1}^{r}\left(1+4\tau^2\sum_{t=0}^{\lfloor{(n-j)/r}\rfloor}\lambda_{j + rt}^2\right)^{-1/4}\le \left(1+4\tau^2\sum_{t=0}^{\lfloor{(n-r)/r}\rfloor}\lambda_{r+rt}^2\right)^{-r/4}\\ &\le \left(1+\frac{4\tau^2}r\sum_{j=r+1}^{n}\lambda_{j}^2\right)^{-r/4}\lesssim_{r} \frac{1}{(1+\tau^2s)^{r/4}}. \\[-48pt] \end{align*} $$
6 Small-ball probability via characteristic functions
Recall that Esseen’s inequality (Theorem 4.7) states that
![]() $\mathcal L(X,\varepsilon )\lesssim \varepsilon \int _{-2/\varepsilon }^{2/\varepsilon }|\varphi _X(t)|\,dt$
for any real random variable X. We will need a ‘relative’ version of Esseen’s inequality, as follows.
$\mathcal L(X,\varepsilon )\lesssim \varepsilon \int _{-2/\varepsilon }^{2/\varepsilon }|\varphi _X(t)|\,dt$
for any real random variable X. We will need a ‘relative’ version of Esseen’s inequality, as follows.
Lemma 6.1. Let
![]() $X,Y$
be real random variables. For any
$X,Y$
be real random variables. For any
![]() $\varepsilon>0$
, we have
$\varepsilon>0$
, we have
 $$\begin{align*}\mathcal L(X,\varepsilon)\lesssim \mathcal L(Y,\varepsilon)+\varepsilon\int_{-2/\varepsilon}^{2/\varepsilon} |\varphi_X(t)-\varphi_Y(t)|\,dt.\end{align*}$$
$$\begin{align*}\mathcal L(X,\varepsilon)\lesssim \mathcal L(Y,\varepsilon)+\varepsilon\int_{-2/\varepsilon}^{2/\varepsilon} |\varphi_X(t)-\varphi_Y(t)|\,dt.\end{align*}$$
In the proof of Lemma 6.1, we use the Fourier transform: For a function
![]() $f\in L^1(\mathbb {R})$
, we write
$f\in L^1(\mathbb {R})$
, we write
Proof of Lemma 6.1
By rescaling it suffices to prove the claim when
![]() $\varepsilon = 1$
. Let us abbreviate the second summand on the right-hand side of the desired inequality by
$\varepsilon = 1$
. Let us abbreviate the second summand on the right-hand side of the desired inequality by
![]() $I := \int _{-2}^2|\varphi _X(t)-\varphi _Y(t)|\,dt$
. Furthermore, let
$I := \int _{-2}^2|\varphi _X(t)-\varphi _Y(t)|\,dt$
. Furthermore, let
![]() (where
(where
![]() $\ast $
denotes convolution); note that
$\ast $
denotes convolution); note that
![]() $0\le \psi (t)\le 2$
for all t, and the support of
$0\le \psi (t)\le 2$
for all t, and the support of
![]() $\psi $
is inside the interval
$\psi $
is inside the interval
![]() $[-2,2]$
. Let
$[-2,2]$
. Let
![]() ; we compute
; we compute
 $$\begin{align*}f(t) =\bigg(\int_{-1}^{1}e^{-itx}\,dx\bigg)^2 =\bigg(\frac{2\sin t}{t}\bigg)^2.\end{align*}$$
$$\begin{align*}f(t) =\bigg(\int_{-1}^{1}e^{-itx}\,dx\bigg)^2 =\bigg(\frac{2\sin t}{t}\bigg)^2.\end{align*}$$
for
![]() $t\neq 0$
and
$t\neq 0$
and
![]() $f(0)=2^2$
. Note that for
$f(0)=2^2$
. Note that for
![]() $|t|\le 1$
we have
$|t|\le 1$
we have
![]() $f(t)\ge 1$
, and for all
$f(t)\ge 1$
, and for all
![]() $t\in \mathbb {R}$
we have
$t\in \mathbb {R}$
we have
![]() $f(t)\le \min \{4,4/t^2\}\leq 8/(t^2+1)$
. By the formula for the Fourier transform and the triangle inequality, for any
$f(t)\le \min \{4,4/t^2\}\leq 8/(t^2+1)$
. By the formula for the Fourier transform and the triangle inequality, for any
![]() $x\in \mathbb {R}$
we have
$x\in \mathbb {R}$
we have
 $$ \begin{align*} |\mathbb{E}[f(X-x)-f(Y-x)]| &= \bigg|\mathbb{E}\int_{-\infty}^{\infty}\psi(\theta)(e^{-i\theta(X-x)}-e^{-i\theta(Y-x)})\,d\theta\bigg|\\ &\le \int_{-\infty}^{\infty}\psi(\theta)\big|\mathbb{E}\big[e^{-i\theta(X-x)}-e^{-i\theta(Y-x)}\big]\big|\,d\theta\\ &=\int_{-\infty}^{\infty}\psi(-t)|\varphi_X(t)-\varphi_Y(t)|\,dt\le 2\int_{-2}^2|\varphi_X(t)-\varphi_Y(t)|\,dt=2I. \end{align*} $$
$$ \begin{align*} |\mathbb{E}[f(X-x)-f(Y-x)]| &= \bigg|\mathbb{E}\int_{-\infty}^{\infty}\psi(\theta)(e^{-i\theta(X-x)}-e^{-i\theta(Y-x)})\,d\theta\bigg|\\ &\le \int_{-\infty}^{\infty}\psi(\theta)\big|\mathbb{E}\big[e^{-i\theta(X-x)}-e^{-i\theta(Y-x)}\big]\big|\,d\theta\\ &=\int_{-\infty}^{\infty}\psi(-t)|\varphi_X(t)-\varphi_Y(t)|\,dt\le 2\int_{-2}^2|\varphi_X(t)-\varphi_Y(t)|\,dt=2I. \end{align*} $$
Now, note that for any
![]() $s\in \mathbb {R}$
we have
$s\in \mathbb {R}$
we have

and therefore
 $$ \begin{align} \Pr[|X-s|\le 1]\le \mathbb{E}[f(Y-s)]+2I&\le \sum_{j\in\mathbb{Z}}\frac{8}{j^2+1}\Pr[|Y-s-j|\le 1] + 2I\\ &\le \mathcal L(Y,1)\sum_{j\in\mathbb Z}\frac8{j^2+1}+2I\le 40\cdot \mathcal L(Y,1)+2I.\notag \end{align} $$
$$ \begin{align} \Pr[|X-s|\le 1]\le \mathbb{E}[f(Y-s)]+2I&\le \sum_{j\in\mathbb{Z}}\frac{8}{j^2+1}\Pr[|Y-s-j|\le 1] + 2I\\ &\le \mathcal L(Y,1)\sum_{j\in\mathbb Z}\frac8{j^2+1}+2I\le 40\cdot \mathcal L(Y,1)+2I.\notag \end{align} $$
Thus,
![]() $\mathcal L(X,1)\le 40\cdot \mathcal L(Y,1)+2I\lesssim L(Y,1)+I$
, as desired.
$\mathcal L(X,1)\le 40\cdot \mathcal L(Y,1)+2I\lesssim L(Y,1)+I$
, as desired.
Next, we will need a slightly more sophisticated exponentially decaying nonuniform version of Lemma 6.1.
Lemma 6.2. Let
![]() $X,Y$
be real random variables. Suppose that for some
$X,Y$
be real random variables. Suppose that for some
![]() $0<\eta <1$
and
$0<\eta <1$
and
![]() $0<\varepsilon \le \sigma $
we have
$0<\varepsilon \le \sigma $
we have
for all
![]() $x\in \mathbb {R}$
. Then for all
$x\in \mathbb {R}$
. Then for all
![]() $x\in \mathbb {R}$
,
$x\in \mathbb {R}$
,
 $$\begin{align*}\Pr[|X-x|\le \varepsilon]\lesssim \frac{\varepsilon^2}{x^2 + \sigma^2}+ \frac{\varepsilon}{\eta\sigma}\exp(-\eta|x|/(2\sigma))+\varepsilon\int_{-2/\varepsilon}^{2/\varepsilon}|\varphi_X(t)-\varphi_Y(t)|\,dt.\end{align*}$$
$$\begin{align*}\Pr[|X-x|\le \varepsilon]\lesssim \frac{\varepsilon^2}{x^2 + \sigma^2}+ \frac{\varepsilon}{\eta\sigma}\exp(-\eta|x|/(2\sigma))+\varepsilon\int_{-2/\varepsilon}^{2/\varepsilon}|\varphi_X(t)-\varphi_Y(t)|\,dt.\end{align*}$$
Proof. As in Lemma 6.1, we may assume that
![]() $\varepsilon = 1$
, and let us again write
$\varepsilon = 1$
, and let us again write
![]() $I := \int _{-2}^2|\varphi _X(t)-\varphi _Y(t)|\,dt$
. Note that the assumption in the lemma statement implies
$I := \int _{-2}^2|\varphi _X(t)-\varphi _Y(t)|\,dt$
. Note that the assumption in the lemma statement implies
![]() $\mathcal L(Y,1)\le 1/(\eta \sigma ) \le e\cdot 1/(\eta \sigma )\cdot \exp (-\eta /2)$
. So if
$\mathcal L(Y,1)\le 1/(\eta \sigma ) \le e\cdot 1/(\eta \sigma )\cdot \exp (-\eta /2)$
. So if
![]() $|x|\le \sigma $
, the desired bound follows from Lemma 6.1. Otherwise, if
$|x|\le \sigma $
, the desired bound follows from Lemma 6.1. Otherwise, if
![]() $|x|\ge \sigma $
, then (6.1) implies
$|x|\ge \sigma $
, then (6.1) implies
 $$ \begin{align*}\Pr[|X-x|\le 1]&\lesssim \sum_{j\in\mathbb{Z}}\frac{\Pr[|Y-x-j|\le 1]}{j^2+1} + I\\ &=\sum_{\substack{j\in\mathbb{Z}\\|j+x|\ge|x|/2}}\frac{\Pr[|Y-x-j|\le 1]}{j^2+1} + \sum_{\substack{j\in\mathbb{Z}\\|j+x|< |x|/2}}\frac{\Pr[|Y-x-j|\le 1]}{j^2+1} + I\\ &\le \sup_{\substack{y\in\mathbb{R}\\|y|\ge |x|/2}}\Pr[|Y-y|\le 1]\cdot \sum_{j\in\mathbb Z}\frac1{j^2+1}+\sum_{\substack{j\in\mathbb{Z}\\|j-(-x)|<|x|/2}}\frac{\Pr[|Y-x-j|\le 1]}{(x/2)^2+1} + I,\\ &\lesssim \frac{\varepsilon}{\eta\sigma}\exp(-\eta|x|/(2\sigma))+\frac{1}{x^2+1}+I \end{align*} $$
$$ \begin{align*}\Pr[|X-x|\le 1]&\lesssim \sum_{j\in\mathbb{Z}}\frac{\Pr[|Y-x-j|\le 1]}{j^2+1} + I\\ &=\sum_{\substack{j\in\mathbb{Z}\\|j+x|\ge|x|/2}}\frac{\Pr[|Y-x-j|\le 1]}{j^2+1} + \sum_{\substack{j\in\mathbb{Z}\\|j+x|< |x|/2}}\frac{\Pr[|Y-x-j|\le 1]}{j^2+1} + I\\ &\le \sup_{\substack{y\in\mathbb{R}\\|y|\ge |x|/2}}\Pr[|Y-y|\le 1]\cdot \sum_{j\in\mathbb Z}\frac1{j^2+1}+\sum_{\substack{j\in\mathbb{Z}\\|j-(-x)|<|x|/2}}\frac{\Pr[|Y-x-j|\le 1]}{(x/2)^2+1} + I,\\ &\lesssim \frac{\varepsilon}{\eta\sigma}\exp(-\eta|x|/(2\sigma))+\frac{1}{x^2+1}+I \end{align*} $$
from which the desired result follows (using that
![]() $x^2+1\geq x^2\gtrsim x^2+\sigma ^2$
since we assumed
$x^2+1\geq x^2\gtrsim x^2+\sigma ^2$
since we assumed
![]() $|x|\ge \sigma $
).
$|x|\ge \sigma $
).
It turns out that these ideas are not only useful for anticoncentration; we can also derive lower bounds on the probability that X is close to some point x, given local control over the behavior of Y near x.
Lemma 6.3. There is an absolute constant
![]() $C_{6.3}$
such that the following holds. Let
$C_{6.3}$
such that the following holds. Let
![]() $X,Y$
be real random variables, and suppose Y is continuous with a density function
$X,Y$
be real random variables, and suppose Y is continuous with a density function
![]() $p_Y$
. Let
$p_Y$
. Let
![]() $\varepsilon>0$
and
$\varepsilon>0$
and
![]() $x\in \mathbb {R}$
, and suppose that
$x\in \mathbb {R}$
, and suppose that
![]() $K\ge 1$
and
$K\ge 1$
and
![]() $R\geq 4$
are such that
$R\geq 4$
are such that
![]() $p_Y(y_1)/p_Y(y_2)\le K$
for all
$p_Y(y_1)/p_Y(y_2)\le K$
for all
![]() $ y_1,y_2\in [x-R\varepsilon ,x+ R\varepsilon ]$
. Then
$ y_1,y_2\in [x-R\varepsilon ,x+ R\varepsilon ]$
. Then
 $$\begin{align*}\Pr[|X-x|\le 10^4K\varepsilon]\ge \frac{1}{8}\Pr[|Y-x|\le \varepsilon]-C_{6.3} \bigg(R^{-1}\mathcal{L}(Y,\varepsilon)+\varepsilon\int_{-2/\varepsilon}^{2/\varepsilon}|\varphi_Y(t)-\varphi_X(t)|\,dt\bigg).\end{align*}$$
$$\begin{align*}\Pr[|X-x|\le 10^4K\varepsilon]\ge \frac{1}{8}\Pr[|Y-x|\le \varepsilon]-C_{6.3} \bigg(R^{-1}\mathcal{L}(Y,\varepsilon)+\varepsilon\int_{-2/\varepsilon}^{2/\varepsilon}|\varphi_Y(t)-\varphi_X(t)|\,dt\bigg).\end{align*}$$
The reader may think of K as a constant (in our applications of this lemma, we will take
![]() $K=2$
). We remark that it would be possible to state a cruder version of this lemma with no assumption on the density
$K=2$
). We remark that it would be possible to state a cruder version of this lemma with no assumption on the density
![]() $p_Y$
. This would be sufficient to prove a version of Theorem 3.1 where B also depends on A and H (in addition to depending on C), but this would not be enough for the proof of Theorem 2.1 (for technical reasons discussed in Remark 13.2).
$p_Y$
. This would be sufficient to prove a version of Theorem 3.1 where B also depends on A and H (in addition to depending on C), but this would not be enough for the proof of Theorem 2.1 (for technical reasons discussed in Remark 13.2).
Proof. It again suffices to prove the claim when
![]() $\varepsilon = 1$
. Let the function f and
$\varepsilon = 1$
. Let the function f and
![]() $I:= \int _{-2}^2|\varphi _X(t)-\varphi _Y(t)|\,dt$
be as in the proof of Lemma 6.1, and recall that
$I:= \int _{-2}^2|\varphi _X(t)-\varphi _Y(t)|\,dt$
be as in the proof of Lemma 6.1, and recall that
![]() for all
for all
![]() $t\in \mathbb {R}$
and furthermore
$t\in \mathbb {R}$
and furthermore
![]() $|\mathbb E[f(X-x)]-\mathbb E[f(Y-x)]|\le 2I$
. We have
$|\mathbb E[f(X-x)]-\mathbb E[f(Y-x)]|\le 2I$
. We have

As in (6.1), we have
 $$\begin{align*}\Pr[|X-x-j|\le 1]\le \sum_{k\in\mathbb{Z}}\frac{8}{k^2+1}\Pr[|Y-x-j-k|\le 1] + 2I,\end{align*}$$
$$\begin{align*}\Pr[|X-x-j|\le 1]\le \sum_{k\in\mathbb{Z}}\frac{8}{k^2+1}\Pr[|Y-x-j-k|\le 1] + 2I,\end{align*}$$
so
 $$ \begin{align*} &\sum_{\substack{j\in\mathbb Z\\|j|\ge 9999K}}\frac{2}{j^2+1}\Pr[|X-x-j|\le 1]\le 16\sum_{\substack{j,k\in\mathbb Z\\|j|\ge 9999K}}\frac{\Pr[|Y-x-j-k|\le 1]}{(j^2+1)(k^2+1)}+2\left(\sum_{j\in\mathbb Z}\frac{2}{j^2+1}\right)I\\ &\qquad\le 16\sum_{\substack{j,k\in\mathbb Z\\9999K\le|j|\le (R-1)/2\\|k|\le (R-1)/2}}\frac{K\Pr[|Y-x|\le 1]}{(j^2+1)(k^2+1)} + 16\sum_{\substack{j,k\in \mathbb{Z}\\\max\{|j|,|k|\}> (R-1)/2}}\frac{\mathcal{L}(Y,1)}{(j^2+1)(k^2+1)} + 20I\\ &\qquad\le 16K\cdot \Pr[|Y-x|\le 1]\cdot 5\cdot \frac{2}{9999K-1}+ 16\cdot 2\cdot 5\cdot \frac{2}{(R-3)/2}\cdot \mathcal{L}(Y,1) + 20I\\ &\qquad\le \frac{1}{8}\Pr[|Y-x|\le 1]+O(R^{-1})\cdot \mathcal{L}(Y,1)+O(I), \end{align*} $$
$$ \begin{align*} &\sum_{\substack{j\in\mathbb Z\\|j|\ge 9999K}}\frac{2}{j^2+1}\Pr[|X-x-j|\le 1]\le 16\sum_{\substack{j,k\in\mathbb Z\\|j|\ge 9999K}}\frac{\Pr[|Y-x-j-k|\le 1]}{(j^2+1)(k^2+1)}+2\left(\sum_{j\in\mathbb Z}\frac{2}{j^2+1}\right)I\\ &\qquad\le 16\sum_{\substack{j,k\in\mathbb Z\\9999K\le|j|\le (R-1)/2\\|k|\le (R-1)/2}}\frac{K\Pr[|Y-x|\le 1]}{(j^2+1)(k^2+1)} + 16\sum_{\substack{j,k\in \mathbb{Z}\\\max\{|j|,|k|\}> (R-1)/2}}\frac{\mathcal{L}(Y,1)}{(j^2+1)(k^2+1)} + 20I\\ &\qquad\le 16K\cdot \Pr[|Y-x|\le 1]\cdot 5\cdot \frac{2}{9999K-1}+ 16\cdot 2\cdot 5\cdot \frac{2}{(R-3)/2}\cdot \mathcal{L}(Y,1) + 20I\\ &\qquad\le \frac{1}{8}\Pr[|Y-x|\le 1]+O(R^{-1})\cdot \mathcal{L}(Y,1)+O(I), \end{align*} $$
where we used that
![]() $\sum _{j\in \mathbb Z} 1/(j^2+1)\leq 5$
and
$\sum _{j\in \mathbb Z} 1/(j^2+1)\leq 5$
and
![]() $\sum _{j\in \mathbb Z, |j|\geq T} 1/(j^2+1)\leq 2\sum _{j\in \mathbb Z, j\geq T} 1/(j(j-1)) \le 2/(T-1)$
for
$\sum _{j\in \mathbb Z, |j|\geq T} 1/(j^2+1)\leq 2\sum _{j\in \mathbb Z, j\geq T} 1/(j(j-1)) \le 2/(T-1)$
for
![]() $T> 1$
. Plugging this into (6.3) gives the desired result.
$T> 1$
. Plugging this into (6.3) gives the desired result.
7 Characteristic function estimates based on linear cancellation
Consider X as in Theorem 3.1, and let
![]() $X^*=(X-\mathbb E X)/\sigma (X)$
. When t is not too large, we can prove estimates on
$X^*=(X-\mathbb E X)/\sigma (X)$
. When t is not too large, we can prove estimates on
![]() $\varphi _{X^*}(t)$
purely using the linear behavior of X (treating the quadratic part as an ‘error term’). In this section, we prove two different results of this type.
$\varphi _{X^*}(t)$
purely using the linear behavior of X (treating the quadratic part as an ‘error term’). In this section, we prove two different results of this type.
First, when t is very small, there is essentially no cancellation in
![]() $\varphi _{X^*}(t)$
, and we have the following crude estimate. Roughly speaking, we use the simple observation (from Section 3.1) that X can be interpreted as a sum of independent random variables (a ‘linear part’), plus a ‘quadratic part’ with negligible variance. We can then use standard estimates for characteristic functions of sums of independent random variables.
$\varphi _{X^*}(t)$
, and we have the following crude estimate. Roughly speaking, we use the simple observation (from Section 3.1) that X can be interpreted as a sum of independent random variables (a ‘linear part’), plus a ‘quadratic part’ with negligible variance. We can then use standard estimates for characteristic functions of sums of independent random variables.
Lemma 7.1. Fix
![]() $\varepsilon , H> 0$
. Let G be an n-vertex graph with density at least
$\varepsilon , H> 0$
. Let G be an n-vertex graph with density at least
![]() $\varepsilon $
, and consider
$\varepsilon $
, and consider
![]() $e_0\in \mathbb {R}$
and a vector
$e_0\in \mathbb {R}$
and a vector
![]() $\vec {e}\in \mathbb {R}^{V(G)}$
with
$\vec {e}\in \mathbb {R}^{V(G)}$
with
![]() $0\le e_v\le Hn$
for all
$0\le e_v\le Hn$
for all
![]() $v\in V(G)$
. Let
$v\in V(G)$
. Let
![]() $U\subseteq V(G)$
be a random vertex subset obtained by including each vertex with probability
$U\subseteq V(G)$
be a random vertex subset obtained by including each vertex with probability
![]() $1/2$
independently, and let
$1/2$
independently, and let
![]() $X = e(G[U]) + \sum _{v\in U}e_v + e_0$
. Let
$X = e(G[U]) + \sum _{v\in U}e_v + e_0$
. Let
![]() $X^*=(X-\mathbb E X)/\sigma (X)$
, and let
$X^*=(X-\mathbb E X)/\sigma (X)$
, and let
![]() $Z\sim \mathcal N(0,1)$
be a standard normal random variable. Then, for all
$Z\sim \mathcal N(0,1)$
be a standard normal random variable. Then, for all
![]() $t\in \mathbb {R}$
, we have
$t\in \mathbb {R}$
, we have
We remark that on its own Lemma 7.1 implies a central limit theorem (stating that X is asymptotically Gaussian) by Lévy’s continuity theorem (see, for example, [Reference Durrett30, Theorem 3.3.17]).
Proof. Define the random vector
![]() $\vec x\in \{-1,1\}^{V(G)}$
by taking
$\vec x\in \{-1,1\}^{V(G)}$
by taking
![]() $x_v=1$
if
$x_v=1$
if
![]() $v\in U$
, and
$v\in U$
, and
![]() $x_v=-1$
if
$x_v=-1$
if
![]() $v\notin U$
(so
$v\notin U$
(so
![]() $x_v$
for
$x_v$
for
![]() $v\in V(G)$
are independent Rademacher random variables). Then, we compute
$v\in V(G)$
are independent Rademacher random variables). Then, we compute
 $$ \begin{align*} X &= e_0+\frac{e(G)}{4}+\frac{1}{2}\sum_{v\in V(G)} e_v+\frac{1}{2}\sum_{v\in V(G)}\Big(e_v+\frac{1}{2}\deg_G(v)\Big)x_v + \frac{1}{4}\sum_{uv\in E(G)}x_ux_v\\ &=\mathbb E X+\frac{1}{2}\sum_{v\in V(G)}\left(e_{v}+\frac{1}{2}\deg_{G}(v)\right)x_{v}+\frac{1}{4}\sum_{uv\in E(G)}x_{u}x_{v}, \end{align*} $$
$$ \begin{align*} X &= e_0+\frac{e(G)}{4}+\frac{1}{2}\sum_{v\in V(G)} e_v+\frac{1}{2}\sum_{v\in V(G)}\Big(e_v+\frac{1}{2}\deg_G(v)\Big)x_v + \frac{1}{4}\sum_{uv\in E(G)}x_ux_v\\ &=\mathbb E X+\frac{1}{2}\sum_{v\in V(G)}\left(e_{v}+\frac{1}{2}\deg_{G}(v)\right)x_{v}+\frac{1}{4}\sum_{uv\in E(G)}x_{u}x_{v}, \end{align*} $$
as in (3.1). Defining
![]() $d_v = e_v+\deg _G(v)/2$
for
$d_v = e_v+\deg _G(v)/2$
for
![]() $v\in V(G)$
, we deduce that
$v\in V(G)$
, we deduce that
 $$\begin{align*}X-\mathbb{E}X=\frac{1}{2}\vec{d}\cdot\vec{x}+\frac{1}{4}\sum_{uv\in E(G)}x_ux_v.\end{align*}$$
$$\begin{align*}X-\mathbb{E}X=\frac{1}{2}\vec{d}\cdot\vec{x}+\frac{1}{4}\sum_{uv\in E(G)}x_ux_v.\end{align*}$$
That is to say,
![]() $X-\mathbb E X$
has a ‘linear part’
$X-\mathbb E X$
has a ‘linear part’
![]() $\frac {1}{2}\vec d\cdot \vec x$
and a ‘quadratic part’
$\frac {1}{2}\vec d\cdot \vec x$
and a ‘quadratic part’
![]() $\frac {1}{4}\sum _{uv\in E(G)}x_ux_v$
. Recalling (4.5), we have
$\frac {1}{4}\sum _{uv\in E(G)}x_ux_v$
. Recalling (4.5), we have
![]() $\sigma (X)^2 = \frac {1}{4}\lVert \vec {d}\rVert _2^2 + \frac {1}{16}e(G)\geq \frac {1}{4}\lVert \vec {d}\rVert _2^2\ge \frac {1}{4}\lVert \vec {d}\rVert _1^2/n \gtrsim _{\varepsilon } n^3$
(here, we are using our density assumption as well as the assumption that
$\sigma (X)^2 = \frac {1}{4}\lVert \vec {d}\rVert _2^2 + \frac {1}{16}e(G)\geq \frac {1}{4}\lVert \vec {d}\rVert _2^2\ge \frac {1}{4}\lVert \vec {d}\rVert _1^2/n \gtrsim _{\varepsilon } n^3$
(here, we are using our density assumption as well as the assumption that
![]() $e_v\geq 0$
for all
$e_v\geq 0$
for all
![]() $v\in V(G)$
).
$v\in V(G)$
).
First, we compare
![]() $X^*=(X-\mathbb E X)/\sigma (X)$
to its linear part
$X^*=(X-\mathbb E X)/\sigma (X)$
to its linear part
![]() $(\vec d\cdot \vec x)/(2\sigma (X))$
. For all
$(\vec d\cdot \vec x)/(2\sigma (X))$
. For all
![]() $t\in \mathbb {R}$
, we have
$t\in \mathbb {R}$
, we have
![]() $|\exp (it)-1|\le |t|$
and therefore
$|\exp (it)-1|\le |t|$
and therefore
 $$ \begin{align} \Big|\varphi_{X^*}(t)&-\mathbb{E}[e^{it(\vec{d}\cdot\vec{x})/(2\sigma(X))}]\Big|\le \mathbb{E}\Big|\exp\Big(\frac{it}{4\sigma(X)}\sum_{uv\in E(G)}x_ux_v\Big)-1\Big|\le\frac{|t|}{4\sigma(X)}\mathbb{E}\Big|\sum_{uv\in E(G)}x_ux_v\Big|\notag\\ &\le\frac{|t|}{4\sigma(X)}\left(\mathbb{E}\Big[\Big(\sum_{uv\in E(G)}x_ux_v\Big)^2\Big]\right)^{1/2}=\frac{|t|}{4\sigma(X)}\cdot e(G)^{1/2}\leq \frac{|t|}{\Omega_{\varepsilon}(n^{3/2})}\cdot n\lesssim_{\varepsilon} |t|n^{-1/2}. \end{align} $$
$$ \begin{align} \Big|\varphi_{X^*}(t)&-\mathbb{E}[e^{it(\vec{d}\cdot\vec{x})/(2\sigma(X))}]\Big|\le \mathbb{E}\Big|\exp\Big(\frac{it}{4\sigma(X)}\sum_{uv\in E(G)}x_ux_v\Big)-1\Big|\le\frac{|t|}{4\sigma(X)}\mathbb{E}\Big|\sum_{uv\in E(G)}x_ux_v\Big|\notag\\ &\le\frac{|t|}{4\sigma(X)}\left(\mathbb{E}\Big[\Big(\sum_{uv\in E(G)}x_ux_v\Big)^2\Big]\right)^{1/2}=\frac{|t|}{4\sigma(X)}\cdot e(G)^{1/2}\leq \frac{|t|}{\Omega_{\varepsilon}(n^{3/2})}\cdot n\lesssim_{\varepsilon} |t|n^{-1/2}. \end{align} $$
Next, the linear part can be handled as in a standard proof of a quantitative central limit theorem (c.f. Lemma 5.5). Let
![]() $\sigma _1 = \sigma (\vec {d}\cdot \vec {x})=\lVert \vec {d}\rVert _2$
and
$\sigma _1 = \sigma (\vec {d}\cdot \vec {x})=\lVert \vec {d}\rVert _2$
and
![]() $\Gamma = (\sum _{v\in V(G)}d_v^2)^{3/2}/\sum _{v\in V(G)}d_v^3\gtrsim _H \lVert \vec {d}\rVert _2^3/n^4\gtrsim _{\varepsilon ,H} n^{1/2}$
(recalling that
$\Gamma = (\sum _{v\in V(G)}d_v^2)^{3/2}/\sum _{v\in V(G)}d_v^3\gtrsim _H \lVert \vec {d}\rVert _2^3/n^4\gtrsim _{\varepsilon ,H} n^{1/2}$
(recalling that
![]() $\lVert \vec {d}\rVert _2^2 \gtrsim _{\varepsilon } n^3$
), and note that
$\lVert \vec {d}\rVert _2^2 \gtrsim _{\varepsilon } n^3$
), and note that
![]() $\varphi _Z(u) = e^{-u^2/2}$
. For
$\varphi _Z(u) = e^{-u^2/2}$
. For
![]() $|u|\le \Gamma /4$
, we have
$|u|\le \Gamma /4$
, we have
by [Reference Petrov and Brown83, Chapter V, Lemma 1]. This yields
for all
![]() $u\in \mathbb {R}$
(this is trivial for
$u\in \mathbb {R}$
(this is trivial for
![]() $|u|\ge \Gamma /4 \gtrsim _{\varepsilon ,H} n^{1/2}$
). Taking
$|u|\ge \Gamma /4 \gtrsim _{\varepsilon ,H} n^{1/2}$
). Taking
![]() $u = t\sigma _1/(2\sigma (X))$
and using
$u = t\sigma _1/(2\sigma (X))$
and using
![]() $\sigma _1/(2\sigma (X)) = \lVert \vec {d}\rVert _2/(\lVert \vec {d}\rVert _2^2 + \frac {1}{4}e(G))^{1/2}=1-O_{\varepsilon }(n^{-1})$
, we have
$\sigma _1/(2\sigma (X)) = \lVert \vec {d}\rVert _2/(\lVert \vec {d}\rVert _2^2 + \frac {1}{4}e(G))^{1/2}=1-O_{\varepsilon }(n^{-1})$
, we have
Here, we used that the function
![]() $\varphi _Z(u)=e^{-u^2/2}$
has bounded derivative, and therefore
$\varphi _Z(u)=e^{-u^2/2}$
has bounded derivative, and therefore
![]() $|\varphi _Z(u)-\varphi _Z(t)|\lesssim |u-t|=|\sigma _1/(2\sigma (X))-1|\cdot |t|=O_{\varepsilon }(n^{-1}|t|)$
. The desired inequality now follows from (7.1) and (7.2).
$|\varphi _Z(u)-\varphi _Z(t)|\lesssim |u-t|=|\sigma _1/(2\sigma (X))-1|\cdot |t|=O_{\varepsilon }(n^{-1}|t|)$
. The desired inequality now follows from (7.1) and (7.2).
As mentioned above, Lemma 7.1 will be used for very small t. When t is somewhat larger we will need a stronger bound which takes into account the interaction between the linear and quadratic parts of our random variable. Specifically, writing
![]() $Z_1$
and
$Z_1$
and
![]() $Z_2$
for the linear and quadratic parts of our normalized random variable
$Z_2$
for the linear and quadratic parts of our normalized random variable
![]() $X^*$
, we show that
$X^*$
, we show that
![]() $e^{itZ_2}$
does not ‘correlate adversarially’ with
$e^{itZ_2}$
does not ‘correlate adversarially’ with
![]() $e^{itZ_1}$
, using an argument due to Berkowitz [Reference Berkowitz12]. Roughly speaking, the idea is as follows. Considering
$e^{itZ_1}$
, using an argument due to Berkowitz [Reference Berkowitz12]. Roughly speaking, the idea is as follows. Considering
![]() $\vec x\in \{-1,1\}^{V(G)}$
as in the proof of Lemma 7.1, we can apply Taylor’s theorem to the exponential function to approximate
$\vec x\in \{-1,1\}^{V(G)}$
as in the proof of Lemma 7.1, we can apply Taylor’s theorem to the exponential function to approximate
![]() $e^{itZ_2}$
by a polynomial in
$e^{itZ_2}$
by a polynomial in
![]() $Z_2$
, thereby approximating
$Z_2$
, thereby approximating
![]() $\varphi _{X^*}(t)$
by a sum of terms of the form
$\varphi _{X^*}(t)$
by a sum of terms of the form
![]() $\mathbb E[\prod _{i\in S}x_Se^{itZ_1}]$
(where the sets S are rather small). Then, we observe that it is impossible for terms of the form
$\mathbb E[\prod _{i\in S}x_Se^{itZ_1}]$
(where the sets S are rather small). Then, we observe that it is impossible for terms of the form
![]() $\prod _{i\in S}x_S$
to correlate in a pathological way with
$\prod _{i\in S}x_S$
to correlate in a pathological way with
![]() $e^{itZ_1}$
, because all but
$e^{itZ_1}$
, because all but
![]() $|S|$
of the terms in the ‘linear’ random variable
$|S|$
of the terms in the ‘linear’ random variable
![]() $Z_1$
are independent from
$Z_1$
are independent from
![]() $\prod _{i\in S}x_S$
. We can use this observation to prove very strong upper bounds on the magnitude of each of our terms
$\prod _{i\in S}x_S$
. We can use this observation to prove very strong upper bounds on the magnitude of each of our terms
![]() $\mathbb E[\prod _{i\in S}x_Se^{itZ_1}]$
(we do not attempt to understand any potential cancellation between these terms, but the resulting loss is not severe as there are not many choices of S).
$\mathbb E[\prod _{i\in S}x_Se^{itZ_1}]$
(we do not attempt to understand any potential cancellation between these terms, but the resulting loss is not severe as there are not many choices of S).
In some range of t, the above idea can be used to prove a much stronger bound than in Lemma 7.1 (where we obtained a bound of
![]() $|t|n^{-1/2}$
). However, naïvely, this idea is only suitable in the regime
$|t|n^{-1/2}$
). However, naïvely, this idea is only suitable in the regime
![]() $|t|\lesssim \sqrt n$
, for two reasons. The first reason is that (one can compute that) the typical order of magnitude of
$|t|\lesssim \sqrt n$
, for two reasons. The first reason is that (one can compute that) the typical order of magnitude of
![]() $Z_2$
is about
$Z_2$
is about
![]() $1/\sqrt n$
, so a Taylor series approximation for
$1/\sqrt n$
, so a Taylor series approximation for
![]() $e^{itZ_2}$
becomes increasingly ineffective as
$e^{itZ_2}$
becomes increasingly ineffective as
![]() $|t|$
increases past
$|t|$
increases past
![]() $\sqrt n$
. The second reason is that depending on the structure of our graph G it is possible that
$\sqrt n$
. The second reason is that depending on the structure of our graph G it is possible that
![]() $|\varphi _{Z_1}(\Theta (\sqrt n))|\gtrsim 1$
, meaning that consideration of the linear part of
$|\varphi _{Z_1}(\Theta (\sqrt n))|\gtrsim 1$
, meaning that consideration of the linear part of
![]() $X^*$
simply does not suffice to prove our desired bound on
$X^*$
simply does not suffice to prove our desired bound on
![]() $\varphi _{X^*}(t)$
(for example, this occurs when
$\varphi _{X^*}(t)$
(for example, this occurs when
![]() $\vec e=\vec 0$
and G is regular).
$\vec e=\vec 0$
and G is regular).
In order to overcome the first of these issues, we restrict our attention to a small vertex subset I, taking advantage of the different way that the linear and quadratic parts scale (related ideas appeared previously in [Reference Berkowitz13]). Specifically, we condition on an outcome of the vertices sampled outside I, leaving only the randomness within I (corresponding to the sequence
![]() $\vec x_I\in \{-1,1\}^I$
). We then redefine
$\vec x_I\in \{-1,1\}^I$
). We then redefine
![]() $Z_1$
and
$Z_1$
and
![]() $Z_2$
to be the linear and quadratic parts of the conditional random variable
$Z_2$
to be the linear and quadratic parts of the conditional random variable
![]() $X^*$
(as a quadratic polynomial in
$X^*$
(as a quadratic polynomial in
![]() $\vec x_I$
). Dropping to a subset in this way significantly reduces the variance of
$\vec x_I$
). Dropping to a subset in this way significantly reduces the variance of
![]() $Z_2$
but may have a much milder effect on
$Z_2$
but may have a much milder effect on
![]() $Z_1$
, in which case the above Taylor expansion techniques described above are effective.
$Z_1$
, in which case the above Taylor expansion techniques described above are effective.
The second issue is more fundamental and is essentially the reason for the case distinction in our proof of Theorem 3.1 (recall Section 3.2). Specifically, the range of t which we are able to consider depends on a certain RLCD (recall the definitions in Section 4.3).
Lemma 7.2. Fix
![]() $C,H> 0$
and
$C,H> 0$
and
![]() $0<\gamma <1/4$
, and let
$0<\gamma <1/4$
, and let
![]() $L = \lceil 100/\gamma \rceil $
. Then there is
$L = \lceil 100/\gamma \rceil $
. Then there is
![]() $\alpha =\alpha (C,H,\gamma )>0$
such that the following holds. Let G be a C-Ramsey graph with n vertices, where n is sufficiently large with respect to
$\alpha =\alpha (C,H,\gamma )>0$
such that the following holds. Let G be a C-Ramsey graph with n vertices, where n is sufficiently large with respect to
![]() $C, H$
and
$C, H$
and
![]() $\gamma $
, and consider
$\gamma $
, and consider
![]() $e_0\in \mathbb {R}$
and a vector
$e_0\in \mathbb {R}$
and a vector
![]() $\vec {e}\in \mathbb {R}^{V(G)}$
with
$\vec {e}\in \mathbb {R}^{V(G)}$
with
![]() $0\le e_v\le Hn$
for all
$0\le e_v\le Hn$
for all
![]() $v\in V(G)$
. Let
$v\in V(G)$
. Let
![]() $\vec {d}\in \mathbb {R}^{V(G)}$
be given by
$\vec {d}\in \mathbb {R}^{V(G)}$
be given by
![]() $d_v = e_v + \deg _G(v)/2$
for all
$d_v = e_v + \deg _G(v)/2$
for all
![]() $v\in V(G)$
. Next, let
$v\in V(G)$
. Next, let
![]() $U\subseteq V(G)$
be a random vertex subset obtained by including each vertex with probability
$U\subseteq V(G)$
be a random vertex subset obtained by including each vertex with probability
![]() $1/2$
independently, and define
$1/2$
independently, and define
![]() $X = e(G[U]) + \sum _{v\in U}e_v+e_0$
. Let
$X = e(G[U]) + \sum _{v\in U}e_v+e_0$
. Let
![]() $X^*=(X-\mathbb E X)/\sigma (X)$
. Then for any
$X^*=(X-\mathbb E X)/\sigma (X)$
. Then for any
![]() $t\in \mathbb {R}$
with
$t\in \mathbb {R}$
with
we have
Before proving Lemma 7.2, we record a simple fact about the vector
![]() $\vec {d}$
in the lemma statement.
$\vec {d}$
in the lemma statement.
Lemma 7.3. Fix
![]() $C>0$
, and let G be a C-Ramsey graph with n vertices, where n is sufficiently large with respect to C. Consider a vector
$C>0$
, and let G be a C-Ramsey graph with n vertices, where n is sufficiently large with respect to C. Consider a vector
![]() $\vec {e}\in \mathbb {R}_{\ge 0}^{V(G)}$
, and define
$\vec {e}\in \mathbb {R}_{\ge 0}^{V(G)}$
, and define
![]() $\vec {d}\in \mathbb {R}^{V(G)}$
by
$\vec {d}\in \mathbb {R}^{V(G)}$
by
![]() $d_v = e_v + \deg _G(v)/2$
for all
$d_v = e_v + \deg _G(v)/2$
for all
![]() $v\in V(G)$
. Then for any subset
$v\in V(G)$
. Then for any subset
![]() $I\subseteq V(G)$
of size
$I\subseteq V(G)$
of size
![]() $|I|\geq \sqrt {n}$
, we have
$|I|\geq \sqrt {n}$
, we have
![]() $\lVert \vec {d}_I\rVert _2\gtrsim _C |I|^{3/2}$
.
$\lVert \vec {d}_I\rVert _2\gtrsim _C |I|^{3/2}$
.
Proof. Note that
![]() $G[I]$
is a
$G[I]$
is a
![]() $(2C)$
-Ramsey graph, so by Theorem 4.1 we have
$(2C)$
-Ramsey graph, so by Theorem 4.1 we have
![]() $e(G[I])\gtrsim _C |I|^2$
. Thus,
$e(G[I])\gtrsim _C |I|^2$
. Thus,
 $$\begin{align*}\lVert\vec{d}_I\rVert_2^2= \sum_{v\in I}\left(e_v+\frac12 \deg_G(v)\right)^2\geq \sum_{v\in V}( \deg_{G[I]}(v)/2)^2\ge |I|\cdot \left(\frac{e(G[I])}{|I|}\right)^2 \gtrsim_C |I|^3.\\[-45pt] \end{align*}$$
$$\begin{align*}\lVert\vec{d}_I\rVert_2^2= \sum_{v\in I}\left(e_v+\frac12 \deg_G(v)\right)^2\geq \sum_{v\in V}( \deg_{G[I]}(v)/2)^2\ge |I|\cdot \left(\frac{e(G[I])}{|I|}\right)^2 \gtrsim_C |I|^3.\\[-45pt] \end{align*}$$
Note that this lemma in particular implies that in the setting of Lemma 7.2 the vector
![]() $\vec {d}$
has fewer than
$\vec {d}$
has fewer than
![]() $n^{1-\gamma }$
zero coordinates, meaning that
$n^{1-\gamma }$
zero coordinates, meaning that
![]() $\widehat {D}_{L,\gamma }(\vec {d})$
is well defined (recall Definition 4.11).
$\widehat {D}_{L,\gamma }(\vec {d})$
is well defined (recall Definition 4.11).
In the proof of Lemma 7.2, we will also use the following Taylor series approximation for the exponential function.
Lemma 7.4. For all
![]() $z\in \mathbb {C}$
and
$z\in \mathbb {C}$
and
![]() $K\in \mathbb {N}$
, we have
$K\in \mathbb {N}$
, we have
 $$\begin{align*}\bigg|e^z - \sum_{j=0}^K\frac{z^j}{j!}\bigg| \le e^{\max\{0,\Re (z)\}}\frac{|z|^{K+1}}{K!}.\end{align*}$$
$$\begin{align*}\bigg|e^z - \sum_{j=0}^K\frac{z^j}{j!}\bigg| \le e^{\max\{0,\Re (z)\}}\frac{|z|^{K+1}}{K!}.\end{align*}$$
Proof. This follows from Taylor’s theorem with the integral form for the remainder: Note that
 $$\begin{align*}\bigg|\int_{0}^{z}e^{t}(z-t)^{K}\,dt\bigg|=|z|^{K+1}\bigg|\int_{0}^{1}e^{sz}(1-s)^{K}\,ds\bigg|\le e^{\max\{0,\Re (z)\}} |z|^{K+1}.\\[-45pt] \end{align*}$$
$$\begin{align*}\bigg|\int_{0}^{z}e^{t}(z-t)^{K}\,dt\bigg|=|z|^{K+1}\bigg|\int_{0}^{1}e^{sz}(1-s)^{K}\,ds\bigg|\le e^{\max\{0,\Re (z)\}} |z|^{K+1}.\\[-45pt] \end{align*}$$
Now, we prove Lemma 7.2.
Proof of Lemma 7.2
Let us define
![]() $\vec x\in \{-1,1\}^{V(G)}$
by taking
$\vec x\in \{-1,1\}^{V(G)}$
by taking
![]() $x_v=1$
if
$x_v=1$
if
![]() $v\in U$
, and
$v\in U$
, and
![]() $x_v=-1$
if
$x_v=-1$
if
![]() $v\notin U$
(and note that then
$v\notin U$
(and note that then
![]() $\vec {x}$
is a vector of independent Rademacher random variables). As in the proof of Lemma 7.1, we obtain
$\vec {x}$
is a vector of independent Rademacher random variables). As in the proof of Lemma 7.1, we obtain
![]() $X-\mathbb {E}X=\frac {1}{2}\vec {d}\cdot \vec {x}+\frac {1}{4}\sum _{uv\in E(G)}x_ux_v$
and
$X-\mathbb {E}X=\frac {1}{2}\vec {d}\cdot \vec {x}+\frac {1}{4}\sum _{uv\in E(G)}x_ux_v$
and
![]() $\sigma (X) \gtrsim _C n^{3/2}$
(here, we used that by Theorem 4.1 the graph G has density at least
$\sigma (X) \gtrsim _C n^{3/2}$
(here, we used that by Theorem 4.1 the graph G has density at least
![]() $\varepsilon $
for some
$\varepsilon $
for some
![]() $\varepsilon =\varepsilon (C)>0$
only depending on C). We furthermore have
$\varepsilon =\varepsilon (C)>0$
only depending on C). We furthermore have
![]() $\sigma (X) = (\frac {1}{4}\lVert \vec {d}\rVert _2^2+\frac {1}{16}e(G))^{1/2}\lesssim _H n^{3/2}$
.
$\sigma (X) = (\frac {1}{4}\lVert \vec {d}\rVert _2^2+\frac {1}{16}e(G))^{1/2}\lesssim _H n^{3/2}$
.
By the definition of RLCD (Definition 4.11), there is a subset
![]() $I\subseteq V(G)$
of size
$I\subseteq V(G)$
of size
![]() $|I|=\lceil n^{1-\gamma }\rceil $
such that
$|I|=\lceil n^{1-\gamma }\rceil $
such that
Step 1: Reducing to the randomness of
![]() $\vec x_I$
. The first step is to condition on a typical outcome of
$\vec x_I$
. The first step is to condition on a typical outcome of
![]() $\vec x_{V(G)\setminus I}\in \{-1,1\}^{V(G)\setminus I}$
so that we can work purely with the randomness of
$\vec x_{V(G)\setminus I}\in \{-1,1\}^{V(G)\setminus I}$
so that we can work purely with the randomness of
![]() $\vec x_I\in \{-1,1\}^I$
. Define the vector
$\vec x_I\in \{-1,1\}^I$
. Define the vector
![]() $\vec y\in \mathbb R^I$
by taking
$\vec y\in \mathbb R^I$
by taking
 $$\begin{align*}y_v =\frac 14\sum_{\substack{u\in V(G)\setminus I\\uv\in E(G)}} x_u\end{align*}$$
$$\begin{align*}y_v =\frac 14\sum_{\substack{u\in V(G)\setminus I\\uv\in E(G)}} x_u\end{align*}$$
for each
![]() $v\in I$
. Also, let
$v\in I$
. Also, let
 $$\begin{align*}Z_1=\Big(\frac{1}{2}\vec d_I+\vec y\Big)\cdot \vec x_I,\quad\quad Z_2=\frac{1}{4}\sum_{\substack{u,v\in I\\uv\in E(G)}}x_ux_v.\end{align*}$$
$$\begin{align*}Z_1=\Big(\frac{1}{2}\vec d_I+\vec y\Big)\cdot \vec x_I,\quad\quad Z_2=\frac{1}{4}\sum_{\substack{u,v\in I\\uv\in E(G)}}x_ux_v.\end{align*}$$
Note that
![]() $X-\mathbb E[X|\vec x_{V(G)\setminus I}]=Z_1+Z_2$
. Using the fact that
$X-\mathbb E[X|\vec x_{V(G)\setminus I}]=Z_1+Z_2$
. Using the fact that
![]() $|\mathbb E [e^{it (Y+c)}]|=|\mathbb E [e^{it Y}]|$
for any real random variable Y and nonrandom
$|\mathbb E [e^{it (Y+c)}]|=|\mathbb E [e^{it Y}]|$
for any real random variable Y and nonrandom
![]() $c\in \mathbb {R}$
, we have
$c\in \mathbb {R}$
, we have
 $$ \begin{align*} |\varphi_{X^*}(t)|=|\mathbb{E}[e^{itX/\sigma(X)}]| \le \mathbb{E}|\mathbb{E}[e^{itX/\sigma(X)}|\vec{x}_{V(G)\setminus I}]| =\mathbb{E}\left|\mathbb{E}\left[\exp\left(\frac{it(Z_1+Z_2)}{\sigma(X)}\right)\middle|\vec{x}_{V(G)\setminus I}\right]\right|. \end{align*} $$
$$ \begin{align*} |\varphi_{X^*}(t)|=|\mathbb{E}[e^{itX/\sigma(X)}]| \le \mathbb{E}|\mathbb{E}[e^{itX/\sigma(X)}|\vec{x}_{V(G)\setminus I}]| =\mathbb{E}\left|\mathbb{E}\left[\exp\left(\frac{it(Z_1+Z_2)}{\sigma(X)}\right)\middle|\vec{x}_{V(G)\setminus I}\right]\right|. \end{align*} $$
The inner expectation on the right-hand side always has magnitude at most 1. Since
![]() $\deg _G(v)\leq n$
for
$\deg _G(v)\leq n$
for
![]() $v\in I$
, with a Chernoff bound we see that with probability at least
$v\in I$
, with a Chernoff bound we see that with probability at least
![]() $1-\exp (-\Omega (n^{\gamma /4}))$
we have
$1-\exp (-\Omega (n^{\gamma /4}))$
we have
![]() $|y_v|\le n^{1/2+\gamma /8}$
for all
$|y_v|\le n^{1/2+\gamma /8}$
for all
![]() $v\in I$
. Conditioning on a fixed outcome of
$v\in I$
. Conditioning on a fixed outcome of
![]() $\vec x_{V(G)\setminus I}$
such that this is the case, it now suffices to show that
$\vec x_{V(G)\setminus I}$
such that this is the case, it now suffices to show that
 $$ \begin{align} \left|\mathbb{E}\left[\exp\left(\frac{it(Z_1+Z_2)}{\sigma(X)}\right)\right]\right|\lesssim_{C,H,\gamma}n^{-5} \end{align} $$
$$ \begin{align} \left|\mathbb{E}\left[\exp\left(\frac{it(Z_1+Z_2)}{\sigma(X)}\right)\right]\right|\lesssim_{C,H,\gamma}n^{-5} \end{align} $$
for all
![]() $t\in \mathbb {R}$
with
$t\in \mathbb {R}$
with
![]() $n^{2\gamma }\le |t|\le \alpha \cdot \min \{n^{\gamma /2}\widehat {D}_{L,\gamma }(\vec {d}), n^{1/2+\gamma /8}\}$
, where
$n^{2\gamma }\le |t|\le \alpha \cdot \min \{n^{\gamma /2}\widehat {D}_{L,\gamma }(\vec {d}), n^{1/2+\gamma /8}\}$
, where
![]() $\alpha =\alpha (C,H,\gamma )>0$
is chosen sufficiently small (in particular, we may assume
$\alpha =\alpha (C,H,\gamma )>0$
is chosen sufficiently small (in particular, we may assume
![]() $\alpha <1$
).
$\alpha <1$
).
Step 2: Taylor expansion. Let
![]() $K = \lceil 10/\gamma \rceil $
. By Lemma 7.4, we have
$K = \lceil 10/\gamma \rceil $
. By Lemma 7.4, we have
 $$ \begin{align} \bigg|\mathbb{E}\bigg[\exp\!\bigg(\frac{it(Z_1+Z_2)}{\sigma(X)}\bigg)\bigg]\bigg| &= \bigg|\mathbb{E}\bigg[\exp\!\bigg(\frac{itZ_1}{\sigma(X)}\bigg)\exp\!\bigg(\frac{itZ_2}{\sigma(X)}\bigg)\bigg]\bigg|\notag\\ &\le \bigg|\mathbb{E}\bigg[\exp\!\bigg(\frac{itZ_1}{\sigma(X)}\bigg)\sum_{j=0}^{K}\frac{1}{j!}\bigg(\frac{itZ_2}{\sigma(X)}\bigg)^{j}\bigg]\bigg| + \mathbb{E}\bigg[\frac{1}{K!}\bigg(\frac{|tZ_2|}{\sigma(X)}\bigg)^{K+1}\bigg]. \end{align} $$
$$ \begin{align} \bigg|\mathbb{E}\bigg[\exp\!\bigg(\frac{it(Z_1+Z_2)}{\sigma(X)}\bigg)\bigg]\bigg| &= \bigg|\mathbb{E}\bigg[\exp\!\bigg(\frac{itZ_1}{\sigma(X)}\bigg)\exp\!\bigg(\frac{itZ_2}{\sigma(X)}\bigg)\bigg]\bigg|\notag\\ &\le \bigg|\mathbb{E}\bigg[\exp\!\bigg(\frac{itZ_1}{\sigma(X)}\bigg)\sum_{j=0}^{K}\frac{1}{j!}\bigg(\frac{itZ_2}{\sigma(X)}\bigg)^{j}\bigg]\bigg| + \mathbb{E}\bigg[\frac{1}{K!}\bigg(\frac{|tZ_2|}{\sigma(X)}\bigg)^{K+1}\bigg]. \end{align} $$
Recalling that
![]() $|I|=\lceil n^{1-\gamma }\rceil $
and our assumption that
$|I|=\lceil n^{1-\gamma }\rceil $
and our assumption that
![]() $|t|\leq n^{1/2+\gamma /8}$
, we have
$|t|\leq n^{1/2+\gamma /8}$
, we have
 $$\begin{align*}\mathbb{E}[(tZ_2/\sigma(X))^2]=\frac{t^2}{\sigma(X)^2}\cdot \mathbb{E}[Z_2^2]\le \frac{t^2}{\sigma(X)^2}\cdot |I|^2\lesssim_{C} \frac{n^{1+\gamma/4}}{n^3}\cdot n^{2-2\gamma}= n^{-7\gamma/4}.\end{align*}$$
$$\begin{align*}\mathbb{E}[(tZ_2/\sigma(X))^2]=\frac{t^2}{\sigma(X)^2}\cdot \mathbb{E}[Z_2^2]\le \frac{t^2}{\sigma(X)^2}\cdot |I|^2\lesssim_{C} \frac{n^{1+\gamma/4}}{n^3}\cdot n^{2-2\gamma}= n^{-7\gamma/4}.\end{align*}$$
By Theorem 4.14 (hypercontractivity), we deduce
![]() $\mathbb {E}[(|tZ_2|/\sigma (X))^{K+1}]\lesssim _{C,\gamma } n^{-7\gamma (K+1)/8}$
. Thus, using that
$\mathbb {E}[(|tZ_2|/\sigma (X))^{K+1}]\lesssim _{C,\gamma } n^{-7\gamma (K+1)/8}$
. Thus, using that
![]() $(K+1)\gamma \geq 10$
, we obtain
$(K+1)\gamma \geq 10$
, we obtain
 $$ \begin{align} \mathbb{E}\bigg[\frac{1}{K!}\bigg(\frac{|tZ_2|}{\sigma(X)}\bigg)^{K+1}\bigg]\lesssim_{C,\gamma}n^{-5}. \end{align} $$
$$ \begin{align} \mathbb{E}\bigg[\frac{1}{K!}\bigg(\frac{|tZ_2|}{\sigma(X)}\bigg)^{K+1}\bigg]\lesssim_{C,\gamma}n^{-5}. \end{align} $$
Also, note that
![]() $\sum _{j=0}^{K}\frac {1}{j!}(itZ_2/\sigma (X))^{j}$
is a polynomial of degree
$\sum _{j=0}^{K}\frac {1}{j!}(itZ_2/\sigma (X))^{j}$
is a polynomial of degree
![]() $2K$
in
$2K$
in
![]() $\vec x_I$
. Noting that
$\vec x_I$
. Noting that
![]() $x_v^2 = 1$
for all v, one can represent this polynomial as a linear combination of at most
$x_v^2 = 1$
for all v, one can represent this polynomial as a linear combination of at most
![]() $|I|^{2K}<n^{2K}$
multilinear monomials
$|I|^{2K}<n^{2K}$
multilinear monomials
![]() $\prod _{v\in S}x_v$
with
$\prod _{v\in S}x_v$
with
![]() $|S|\leq 2K$
. The coefficient of each such monomial has absolute value
$|S|\leq 2K$
. The coefficient of each such monomial has absolute value
![]() $O_{C,\gamma }(1)$
, recalling that
$O_{C,\gamma }(1)$
, recalling that
![]() $|t|\le n^{1/2+\gamma /8}$
and
$|t|\le n^{1/2+\gamma /8}$
and
![]() $\sigma (X)=\Omega _C(n^{3/2})$
and
$\sigma (X)=\Omega _C(n^{3/2})$
and
![]() $|I|=\lceil n^{1-\gamma }\rceil $
(and
$|I|=\lceil n^{1-\gamma }\rceil $
(and
![]() $K=\lceil 10/\gamma \rceil $
). For the rest of the proof, our goal is now to show that for any set
$K=\lceil 10/\gamma \rceil $
). For the rest of the proof, our goal is now to show that for any set
![]() $S\subseteq I$
with
$S\subseteq I$
with
![]() $|S|\le 2K$
we have
$|S|\le 2K$
we have
 $$ \begin{align} \bigg|\mathbb{E}\bigg[\exp\!\bigg(\frac{itZ_1}{\sigma(X)}\bigg)\prod_{v\in S}x_v\bigg]\bigg|\lesssim_{C,H,\gamma} n^{-5-2K}. \end{align} $$
$$ \begin{align} \bigg|\mathbb{E}\bigg[\exp\!\bigg(\frac{itZ_1}{\sigma(X)}\bigg)\prod_{v\in S}x_v\bigg]\bigg|\lesssim_{C,H,\gamma} n^{-5-2K}. \end{align} $$
The desired bound (7.3) will then follow from (7.4), bounding the first summand by summing (7.6) over all choices of S and bounding the second summand via (7.5).
Step 3: Relating to the LCD. So let us fix some subset
![]() $S\subseteq I$
with
$S\subseteq I$
with
![]() $|S|\le 2K$
. Let
$|S|\le 2K$
. Let
![]() $\vec f=\frac {1}{2}\vec d_I+\vec y\in \mathbb {R}^I$
, so
$\vec f=\frac {1}{2}\vec d_I+\vec y\in \mathbb {R}^I$
, so
![]() $Z_1=\vec f\cdot \vec x_I$
. Noting that
$Z_1=\vec f\cdot \vec x_I$
. Noting that
![]() $|x_v|\le 1$
for all
$|x_v|\le 1$
for all
![]() $v\in I$
, and using (4.2), we have
$v\in I$
, and using (4.2), we have
 $$ \begin{align} \bigg|\mathbb{E}\bigg[\exp\!\bigg(\frac{itZ_1}{\sigma(X)}\bigg)\prod_{v\in S}x_v\bigg]\bigg| &= \bigg|\mathbb{E}\bigg[\prod_{v\in I\setminus S}\exp\!\bigg(\frac{itf_vx_v}{2\sigma(X)}\bigg)\cdot \prod_{v\in S}\exp\!\bigg(\frac{itf_vx_v}{2\sigma(X)}\bigg)x_v\bigg]\bigg|\notag\\ &\le \prod_{v\in I\setminus S} \bigg|\mathbb{E}\bigg[\exp\!\bigg(\frac{itf_vx_v}{2\sigma(X)}\bigg)\bigg]\bigg|\le \exp\left(-\sum_{v\in I\setminus S}\bigg\lVert\frac{tf_v}{2\pi\sigma(X)}\bigg\rVert_{\mathbb{R}/\mathbb{Z}}^2\right)\notag\\ &\le\exp\left(|S|-\operatorname{dist}\!\bigg(\frac{|t|\vec f}{2\pi\sigma(X)},\mathbb{Z}^{I}\bigg)^2\right). \end{align} $$
$$ \begin{align} \bigg|\mathbb{E}\bigg[\exp\!\bigg(\frac{itZ_1}{\sigma(X)}\bigg)\prod_{v\in S}x_v\bigg]\bigg| &= \bigg|\mathbb{E}\bigg[\prod_{v\in I\setminus S}\exp\!\bigg(\frac{itf_vx_v}{2\sigma(X)}\bigg)\cdot \prod_{v\in S}\exp\!\bigg(\frac{itf_vx_v}{2\sigma(X)}\bigg)x_v\bigg]\bigg|\notag\\ &\le \prod_{v\in I\setminus S} \bigg|\mathbb{E}\bigg[\exp\!\bigg(\frac{itf_vx_v}{2\sigma(X)}\bigg)\bigg]\bigg|\le \exp\left(-\sum_{v\in I\setminus S}\bigg\lVert\frac{tf_v}{2\pi\sigma(X)}\bigg\rVert_{\mathbb{R}/\mathbb{Z}}^2\right)\notag\\ &\le\exp\left(|S|-\operatorname{dist}\!\bigg(\frac{|t|\vec f}{2\pi\sigma(X)},\mathbb{Z}^{I}\bigg)^2\right). \end{align} $$
(Here, we used that for any
![]() $\vec a\in \mathbb {R}^I$
we have
$\vec a\in \mathbb {R}^I$
we have
![]() $\sum _{v\in I\setminus S}\|a_v\|_{\mathbb {R}\setminus \mathbb Z}^2=\operatorname {dist} (\vec a_{I\setminus S},\mathbb Z^{I\setminus S})^2\ge \operatorname {dist}(\vec a_{I},\mathbb Z^{I})^2-|S|$
.)
$\sum _{v\in I\setminus S}\|a_v\|_{\mathbb {R}\setminus \mathbb Z}^2=\operatorname {dist} (\vec a_{I\setminus S},\mathbb Z^{I\setminus S})^2\ge \operatorname {dist}(\vec a_{I},\mathbb Z^{I})^2-|S|$
.)
Since
![]() $|t|\le n^{1/2+\gamma /8}$
and
$|t|\le n^{1/2+\gamma /8}$
and
![]() $\sigma (X)=\Omega _C(n^{3/2})$
and we are conditioning on
$\sigma (X)=\Omega _C(n^{3/2})$
and we are conditioning on
![]() $\vec x_{V(G)\setminus I}$
such that
$\vec x_{V(G)\setminus I}$
such that
![]() $|y_v|\le n^{1/2+\gamma /8}$
for all
$|y_v|\le n^{1/2+\gamma /8}$
for all
![]() $v\in I$
, we have (using that
$v\in I$
, we have (using that
![]() $|I|=\lceil n^{1-\gamma }\rceil $
)
$|I|=\lceil n^{1-\gamma }\rceil $
)
 $$\begin{align*}\frac{|t|\lVert\vec{y}\rVert_2}{2\pi\sigma(X)}\lesssim_{C} \frac{n^{1/2+\gamma/8}\cdot (|I|^{1/2})\cdot n^{1/2+\gamma/8}}{n^{3/2}}\lesssim n^{-\gamma/4},\end{align*}$$
$$\begin{align*}\frac{|t|\lVert\vec{y}\rVert_2}{2\pi\sigma(X)}\lesssim_{C} \frac{n^{1/2+\gamma/8}\cdot (|I|^{1/2})\cdot n^{1/2+\gamma/8}}{n^{3/2}}\lesssim n^{-\gamma/4},\end{align*}$$
and therefore
![]() $|t|\lVert \vec {y}\rVert _2/(2\pi \sigma (X))\le 1$
for sufficiently large n. By our assumption
$|t|\lVert \vec {y}\rVert _2/(2\pi \sigma (X))\le 1$
for sufficiently large n. By our assumption
![]() $|t|\le \alpha n^{\gamma /2}\hat {D}_{L,\gamma }(\vec {d})=\alpha n^{\gamma /2}D_{L}(\vec {d}_I/\|\vec d_I\|_2)$
, we have
$|t|\le \alpha n^{\gamma /2}\hat {D}_{L,\gamma }(\vec {d})=\alpha n^{\gamma /2}D_{L}(\vec {d}_I/\|\vec d_I\|_2)$
, we have
 $$\begin{align*}\frac{|t|\lVert\vec{d}_I\rVert_2}{4\pi\sigma(X)}\lesssim_{C,H} \frac{\alpha n^{\gamma/2}D_{L}(\vec{d}_I/\|\vec d_I\|_2)\cdot |I|^{1/2}\cdot n}{n^{3/2}} \lesssim \alpha D_{L}(\vec{d}_I/\|\vec d_I\|_2).\end{align*}$$
$$\begin{align*}\frac{|t|\lVert\vec{d}_I\rVert_2}{4\pi\sigma(X)}\lesssim_{C,H} \frac{\alpha n^{\gamma/2}D_{L}(\vec{d}_I/\|\vec d_I\|_2)\cdot |I|^{1/2}\cdot n}{n^{3/2}} \lesssim \alpha D_{L}(\vec{d}_I/\|\vec d_I\|_2).\end{align*}$$
Hence, by choosing
![]() $\alpha =\alpha (C,H,\gamma )>0$
to be sufficiently small in terms of C, H and
$\alpha =\alpha (C,H,\gamma )>0$
to be sufficiently small in terms of C, H and
![]() $\gamma $
, for sufficiently large n we obtain
$\gamma $
, for sufficiently large n we obtain
![]() $|t|\lVert \vec {d}_I\rVert _2/(4\pi \sigma (X))<D_{L}(\vec {d}_I/\|\vec d_I\|_2)$
and therefore
$|t|\lVert \vec {d}_I\rVert _2/(4\pi \sigma (X))<D_{L}(\vec {d}_I/\|\vec d_I\|_2)$
and therefore
 $$ \begin{align} \operatorname{dist}\!\bigg(\frac{|t|\vec f}{2\pi\sigma(X)},\mathbb{Z}^{I}\bigg)\ge \operatorname{dist}\!\bigg(\frac{|t|(\vec d_I/2)}{2\pi\sigma(X)},\mathbb{Z}^{I}\bigg) - \frac{|t|\lVert\vec{y}\rVert_2}{2\pi\sigma(X)}&\ge\operatorname{dist}\!\bigg(\frac{|t|\lVert\vec{d}_I\rVert_2}{4\pi\sigma(X)}\cdot \frac{\vec{d}_I}{\lVert\vec{d}_I\rVert}_2,\mathbb{Z}^{I}\bigg) - 1\notag\\ &\ge L\sqrt{\log_{+}\bigg(\frac{|t|\lVert\vec{d}_I\rVert_2}{4\pi L\sigma(X)}\bigg)} - 1, \end{align} $$
$$ \begin{align} \operatorname{dist}\!\bigg(\frac{|t|\vec f}{2\pi\sigma(X)},\mathbb{Z}^{I}\bigg)\ge \operatorname{dist}\!\bigg(\frac{|t|(\vec d_I/2)}{2\pi\sigma(X)},\mathbb{Z}^{I}\bigg) - \frac{|t|\lVert\vec{y}\rVert_2}{2\pi\sigma(X)}&\ge\operatorname{dist}\!\bigg(\frac{|t|\lVert\vec{d}_I\rVert_2}{4\pi\sigma(X)}\cdot \frac{\vec{d}_I}{\lVert\vec{d}_I\rVert}_2,\mathbb{Z}^{I}\bigg) - 1\notag\\ &\ge L\sqrt{\log_{+}\bigg(\frac{|t|\lVert\vec{d}_I\rVert_2}{4\pi L\sigma(X)}\bigg)} - 1, \end{align} $$
where we applied the definition of LCD (see Definition 4.9). Now,
![]() $|t|\lVert \vec {d}_I\rVert _2/(4\pi L \sigma (X))\gtrsim _{C,H,\gamma } n^{\gamma /2}$
, since
$|t|\lVert \vec {d}_I\rVert _2/(4\pi L \sigma (X))\gtrsim _{C,H,\gamma } n^{\gamma /2}$
, since
![]() $|t|\ge n^{2\gamma }$
and
$|t|\ge n^{2\gamma }$
and
![]() $\sigma (X)\lesssim _H n^{3/2}$
and
$\sigma (X)\lesssim _H n^{3/2}$
and
![]() $\lVert \vec {d}_I\rVert _2\gtrsim _C|I|^{3/2}\gtrsim n^{(3/2)-3\gamma /2}$
by Lemma 7.3. Thus, for sufficiently large n, we have
$\lVert \vec {d}_I\rVert _2\gtrsim _C|I|^{3/2}\gtrsim n^{(3/2)-3\gamma /2}$
by Lemma 7.3. Thus, for sufficiently large n, we have
![]() $|t|\lVert \vec {d_I}\rVert _2/(4\pi L \sigma (X))\ge n^{\gamma /4}$
, and therefore the term (7.8) is at least
$|t|\lVert \vec {d_I}\rVert _2/(4\pi L \sigma (X))\ge n^{\gamma /4}$
, and therefore the term (7.8) is at least
![]() $L\sqrt {\log _{+}(n^{\gamma /4})}-1\geq (L/2)\sqrt {\log _{+}(n^{\gamma /4})}$
. Then, recalling that
$L\sqrt {\log _{+}(n^{\gamma /4})}-1\geq (L/2)\sqrt {\log _{+}(n^{\gamma /4})}$
. Then, recalling that
![]() $L=\lceil 100/\gamma \rceil $
and
$L=\lceil 100/\gamma \rceil $
and
![]() $K = \lceil 10/\gamma \rceil $
and
$K = \lceil 10/\gamma \rceil $
and
![]() $|S|\leq 2K$
, it follows that
$|S|\leq 2K$
, it follows that
 $$\begin{align*}\operatorname{dist}\!\bigg(\frac{|t|\vec f}{2\pi\sigma(X)},\mathbb{Z}^{I}\bigg)^2 \!\ge \bigg(\frac{L}{2}\sqrt{\log_{+}(n^{\gamma/4})}\bigg)^2 \!\ge \frac{10^{4}}{4\gamma^2}\cdot \frac{\gamma}{4}\log n\ge (4K+5)\log n\ge |S|+(2K+5)\log n.\end{align*}$$
$$\begin{align*}\operatorname{dist}\!\bigg(\frac{|t|\vec f}{2\pi\sigma(X)},\mathbb{Z}^{I}\bigg)^2 \!\ge \bigg(\frac{L}{2}\sqrt{\log_{+}(n^{\gamma/4})}\bigg)^2 \!\ge \frac{10^{4}}{4\gamma^2}\cdot \frac{\gamma}{4}\log n\ge (4K+5)\log n\ge |S|+(2K+5)\log n.\end{align*}$$
Combining this with (7.7), we obtain the desired inequality (7.6).
8 Characteristic function estimates based on quadratic cancellation
In Section 7, we proved some bounds on the characteristic function of a random variable X of the form
![]() $X=e(G[U])+\sum _{v\in U}e_{v}+e_0$
purely using the linear part of X. In this section we prove a bound which purely uses the quadratic part of X (this will be useful for larger t).
$X=e(G[U])+\sum _{v\in U}e_{v}+e_0$
purely using the linear part of X. In this section we prove a bound which purely uses the quadratic part of X (this will be useful for larger t).
In the setting and notation of Section 7, the regime where this result is effective corresponds to a range where
![]() $|t|$
is roughly between
$|t|$
is roughly between
![]() $n^{1/2+\Omega (1)}$
and
$n^{1/2+\Omega (1)}$
and
![]() $n^{3/2}$
. However, the bounds in this section will need to be applied in two slightly different settings (recalling from Section 3.2 that the proof of Theorem 3.1 bifurcates into two cases). To facilitate this, we consider random variables X of a slightly different type than in Section 7: Instead of studying the number of edges in a uniformly random vertex subset, we study the number of edges in a uniformly random vertex subset of a particular size. We can interpret this as studying a conditional distribution, where we condition on an outcome of the number of vertices of our random subset (if desired, we can deduce bounds in the unconditioned setting simply by averaging over all possible outcomes).
$n^{3/2}$
. However, the bounds in this section will need to be applied in two slightly different settings (recalling from Section 3.2 that the proof of Theorem 3.1 bifurcates into two cases). To facilitate this, we consider random variables X of a slightly different type than in Section 7: Instead of studying the number of edges in a uniformly random vertex subset, we study the number of edges in a uniformly random vertex subset of a particular size. We can interpret this as studying a conditional distribution, where we condition on an outcome of the number of vertices of our random subset (if desired, we can deduce bounds in the unconditioned setting simply by averaging over all possible outcomes).
We remark that in this setting where our random subset has a fixed size, it is no longer true that the standard deviation
![]() $\sigma (X)$
must have order of magnitude
$\sigma (X)$
must have order of magnitude
![]() $n^{3/2}$
. Indeed, the order of magnitude of
$n^{3/2}$
. Indeed, the order of magnitude of
![]() $\sigma (X)$
depends on
$\sigma (X)$
depends on
![]() $\vec e$
and the degree sequence of G. Therefore, it is more convenient to study the characteristic function of X directly, instead of its normalized version
$\vec e$
and the degree sequence of G. Therefore, it is more convenient to study the characteristic function of X directly, instead of its normalized version
![]() $X^*=(X-\mathbb EX)/\sigma (X)$
. To avoid confusion, we will use the variable name ‘
$X^*=(X-\mathbb EX)/\sigma (X)$
. To avoid confusion, we will use the variable name ‘
![]() $\tau $
’ instead of ‘t’ when working with characteristic functions of random variables that have not been normalized (so, informally speaking, the translation is that
$\tau $
’ instead of ‘t’ when working with characteristic functions of random variables that have not been normalized (so, informally speaking, the translation is that
![]() $\tau =t/\sigma (X)$
).
$\tau =t/\sigma (X)$
).
Lemma 8.1. Fix
![]() $C>0$
and
$C>0$
and
![]() $0<\eta <1/2$
. There is
$0<\eta <1/2$
. There is
![]() $\nu =\nu (C,\eta )>0$
such that the following holds. Let G be a C-Ramsey graph with n vertices, where n is sufficiently large with respect to C and
$\nu =\nu (C,\eta )>0$
such that the following holds. Let G be a C-Ramsey graph with n vertices, where n is sufficiently large with respect to C and
![]() $\eta $
, and consider a vector
$\eta $
, and consider a vector
![]() $\vec {e}\in \mathbb {R}^{V(G)}$
and
$\vec {e}\in \mathbb {R}^{V(G)}$
and
![]() $e_0\in \mathbb {R}$
. Consider
$e_0\in \mathbb {R}$
. Consider
![]() $\ell \in \mathbb N$
with
$\ell \in \mathbb N$
with
![]() $\eta n\le \ell \le (1-\eta )n$
, and let U be a uniformly random subset of
$\eta n\le \ell \le (1-\eta )n$
, and let U be a uniformly random subset of
![]() $\ell $
vertices in G, and let
$\ell $
vertices in G, and let
![]() $X=e(G[U])+\sum _{v\in U}e_{v}+e_0$
. Then for any
$X=e(G[U])+\sum _{v\in U}e_{v}+e_0$
. Then for any
![]() $\tau \in \mathbb {R}$
with
$\tau \in \mathbb {R}$
with
![]() $n^{-1+\eta }\le |\tau |\le \nu $
we have
$n^{-1+\eta }\le |\tau |\le \nu $
we have
The proof of Lemma 8.1 depends crucially on decoupling techniques. Generally speaking, such techniques allow one to reduce from dependent situations to independent ones (see [Reference de la Peña28] for a book-length treatment). In our context, decoupling allows us to reduce the study of ‘quadratic’ random variables to the study of ‘linear’ ones. Famously, a similar approach was taken by Costello, Tao and Vu [Reference Costello, Tao and Vu27] to study singularity of random symmetric matrices.
To illustrate the basic idea of decoupling, consider an n-variable quadratic polynomial f and a sequence of random variables
![]() $\vec \xi \in \mathbb {R}^n$
. If
$\vec \xi \in \mathbb {R}^n$
. If
![]() $[n]=I\cup J$
is a partition of the index set into two subsets, then we can break
$[n]=I\cup J$
is a partition of the index set into two subsets, then we can break
![]() $\vec \xi =(\xi _1,\ldots ,\xi _n)$
into two subsequences
$\vec \xi =(\xi _1,\ldots ,\xi _n)$
into two subsequences
![]() $\vec \xi _{I}\in \mathbb {R}^I$
and
$\vec \xi _{I}\in \mathbb {R}^I$
and
![]() $\vec \xi _{J}\in \mathbb {R}^J$
(and write
$\vec \xi _{J}\in \mathbb {R}^J$
(and write
![]() $f(\vec \xi )=f(\vec \xi _{I},\vec \xi _{J})$
). Let us assume that the random vectors
$f(\vec \xi )=f(\vec \xi _{I},\vec \xi _{J})$
). Let us assume that the random vectors
![]() $\vec \xi _{I}$
and
$\vec \xi _{I}$
and
![]() $\vec \xi _{J}$
are independent. Now, if
$\vec \xi _{J}$
are independent. Now, if
![]() $\vec \xi _{J}'$
is an independent copy of
$\vec \xi _{J}'$
is an independent copy of
![]() $\vec \xi _{J}$
, then
$\vec \xi _{J}$
, then
![]() $Y:=f(\vec \xi _{I},\vec \xi _{J})-f(\vec \xi _{I},\vec \xi _{J}')$
, is a linear polynomial in
$Y:=f(\vec \xi _{I},\vec \xi _{J})-f(\vec \xi _{I},\vec \xi _{J}')$
, is a linear polynomial in
![]() $\vec \xi _I$
, after conditioning on any outcomes of
$\vec \xi _I$
, after conditioning on any outcomes of
![]() $\vec \xi _J,\vec \xi _J'$
(roughly speaking, this is because ‘the quadratic part in
$\vec \xi _J,\vec \xi _J'$
(roughly speaking, this is because ‘the quadratic part in
![]() $\vec \xi _{I}$
gets cancelled out’). Then, for any
$\vec \xi _{I}$
gets cancelled out’). Then, for any
![]() $\tau \in \mathbb {R}$
, we can use the inequality
$\tau \in \mathbb {R}$
, we can use the inequality
 $$ \begin{align} |\varphi_{f(\vec \xi)}(\tau)|^2=\left|\mathbb E e^{i\tau f(\vec\xi_I,\vec\xi_J)}\right|{}^{2} &\le \mathbb E\left[\left|\mathbb E[e^{i\tau f(\vec\xi_{I},\vec\xi_{J})}\mid \vec\xi_{I}]\right|{}^2\right] = \mathbb E\left[\mathbb E[e^{i\tau (f(\vec\xi_{I},\vec\xi_{J})-f(\vec\xi_{I},\vec\xi_{J}'))}\mid \vec\xi_{I}]\right]\notag \\ & = \mathbb E\left[\mathbb E[e^{i\tau (f(\vec\xi_{I},\vec\xi_{J})-f(\vec\xi_{I},\vec\xi_{J}'))}\mid \vec\xi_{J},\vec\xi_{J}']\right]\notag\\ &\le \mathbb E\left[\left|\mathbb E[e^{i\tau (f(\vec\xi_{I},\vec\xi_{J})-f(\vec\xi_{I},\vec\xi_{J}'))}\mid \vec\xi_{J},\vec\xi_{J}']\right|\right]. \end{align} $$
$$ \begin{align} |\varphi_{f(\vec \xi)}(\tau)|^2=\left|\mathbb E e^{i\tau f(\vec\xi_I,\vec\xi_J)}\right|{}^{2} &\le \mathbb E\left[\left|\mathbb E[e^{i\tau f(\vec\xi_{I},\vec\xi_{J})}\mid \vec\xi_{I}]\right|{}^2\right] = \mathbb E\left[\mathbb E[e^{i\tau (f(\vec\xi_{I},\vec\xi_{J})-f(\vec\xi_{I},\vec\xi_{J}'))}\mid \vec\xi_{I}]\right]\notag \\ & = \mathbb E\left[\mathbb E[e^{i\tau (f(\vec\xi_{I},\vec\xi_{J})-f(\vec\xi_{I},\vec\xi_{J}'))}\mid \vec\xi_{J},\vec\xi_{J}']\right]\notag\\ &\le \mathbb E\left[\left|\mathbb E[e^{i\tau (f(\vec\xi_{I},\vec\xi_{J})-f(\vec\xi_{I},\vec\xi_{J}'))}\mid \vec\xi_{J},\vec\xi_{J}']\right|\right]. \end{align} $$
(This inequality appears as [Reference Kwan and Sauermann65, Lemma 3.3]; similar inequalities appear in [Reference Berkowitz12, Reference Nguyen77].) Crucially, the expression
![]() $\mathbb E[e^{i\tau (f(\vec \xi _{I},\vec \xi _{J})-f(\vec \xi _{I},\vec \xi _{J}'))}\mid \vec \xi _{J},\vec \xi _{J}']$
can be interpreted as an evaluation of the characteristic function of a linear polynomial in
$\mathbb E[e^{i\tau (f(\vec \xi _{I},\vec \xi _{J})-f(\vec \xi _{I},\vec \xi _{J}'))}\mid \vec \xi _{J},\vec \xi _{J}']$
can be interpreted as an evaluation of the characteristic function of a linear polynomial in
![]() $\vec \xi _I$
, which is easy to understand.
$\vec \xi _I$
, which is easy to understand.
In general, (8.1) incurs some loss (one generally obtains bounds which are about the square root of the truth). However, under certain assumptions about the degree-2 part of f, this square-root loss ‘in Fourier space’ does not seriously affect the final bounds one gets ‘in physical space’. Specifically, the first and third authors [Reference Kwan and Sauermann65] observed that it suffices to assume that the degree-2 part of f ‘robustly has high rank’, and observed that quadratic forms associated with Ramsey graphs always satisfy this robust high rank assumption (we will prove a similar statement in Lemma 10.1).
Our proof of Lemma 8.1 will be closely related to the proof of the main result in [Reference Kwan and Sauermann65], although our approach is slightly different, as we need to take more care with quantitative aspects. In particular, instead of working with a qualitative robust-high-rank assumption we will directly make use of the fact that in any Ramsey graph, there are many disjoint tuples of vertices with very different neighborhoods (this can be interpreted as a particular sense in which the adjacency matrix of G robustly has high rank).
Lemma 8.2. For any
![]() $C,\beta>0$
, there is
$C,\beta>0$
, there is
![]() $\zeta =\zeta (C,\beta )>0$
such that the following holds for all sufficiently large n. Let G be a C-Ramsey graph with n vertices, and let
$\zeta =\zeta (C,\beta )>0$
such that the following holds for all sufficiently large n. Let G be a C-Ramsey graph with n vertices, and let
![]() $q=\lfloor \zeta \log n\rfloor $
. Then there is a partition
$q=\lfloor \zeta \log n\rfloor $
. Then there is a partition
![]() $V(G)=I\cup J$
and a collection
$V(G)=I\cup J$
and a collection
![]() $\mathcal {V}\subseteq I^{q}$
of at least
$\mathcal {V}\subseteq I^{q}$
of at least
![]() $n^{1-\beta }$
disjoint q-tuples of vertices in I such that for all
$n^{1-\beta }$
disjoint q-tuples of vertices in I such that for all
![]() $(v_1,\ldots ,v_q)\in \mathcal {V}$
we have
$(v_1,\ldots ,v_q)\in \mathcal {V}$
we have
for all
![]() $r=1,\ldots ,q$
.
$r=1,\ldots ,q$
.
Proof. By Lemma 4.4 (applied with
![]() $m=n^{1-\beta /2}$
and
$m=n^{1-\beta /2}$
and
![]() $\alpha = 1/5$
), for some
$\alpha = 1/5$
), for some
![]() $\rho =\rho (C)$
with
$\rho =\rho (C)$
with
![]() $0<\rho <1$
we can find a vertex subset
$0<\rho <1$
we can find a vertex subset
![]() $R\subseteq V(G)$
with
$R\subseteq V(G)$
with
![]() $|R|\ge n^{1-\beta /2}$
, such that the induced subgraph
$|R|\ge n^{1-\beta /2}$
, such that the induced subgraph
![]() $G[R]$
is
$G[R]$
is
![]() $(n^{-\rho \beta /2},\rho )$
-rich. Let us now define
$(n^{-\rho \beta /2},\rho )$
-rich. Let us now define
![]() $\zeta =\beta \rho /(2\log (1/\rho ))>0$
, and let
$\zeta =\beta \rho /(2\log (1/\rho ))>0$
, and let
![]() $q=\lfloor \zeta \log n\rfloor $
.
$q=\lfloor \zeta \log n\rfloor $
.
We claim that for any subset
![]() $U\subseteq R$
of at size at least
$U\subseteq R$
of at size at least
![]() $|U|>n^{1/5}$
, we can iteratively construct a q-tuple
$|U|>n^{1/5}$
, we can iteratively construct a q-tuple
![]() $(v_{1},\ldots ,v_{q})\in U^q$
with
$(v_{1},\ldots ,v_{q})\in U^q$
with
for
![]() $r=1,\ldots ,q$
. Indeed, for any
$r=1,\ldots ,q$
. Indeed, for any
![]() $0\le k<q$
, consider a k-tuple
$0\le k<q$
, consider a k-tuple
![]() $(v_{1},\ldots ,v_{k})\in U^k$
satisfying (8.3) for
$(v_{1},\ldots ,v_{k})\in U^k$
satisfying (8.3) for
![]() $r=1,\ldots ,k$
. Since
$r=1,\ldots ,k$
. Since
![]() $\rho ^k\ge \rho ^q\geq \rho ^{\zeta \log n}= n^{-\rho \beta /2}$
, we can apply the definition of
$\rho ^k\ge \rho ^q\geq \rho ^{\zeta \log n}= n^{-\rho \beta /2}$
, we can apply the definition of
![]() $G[R]$
being
$G[R]$
being
![]() $(n^{-\rho \beta /2},\rho )$
-rich (see Definition 4.3) to the set
$(n^{-\rho \beta /2},\rho )$
-rich (see Definition 4.3) to the set
![]() $W:=R\setminus (N(v_1)\cup \cdots \cup N(v_k))$
of size
$W:=R\setminus (N(v_1)\cup \cdots \cup N(v_k))$
of size
![]() $|W|\geq \rho ^k|R|$
and conclude that there are at most
$|W|\geq \rho ^k|R|$
and conclude that there are at most
![]() $|R|^{1/5}\leq n^{1/5}$
vertices
$|R|^{1/5}\leq n^{1/5}$
vertices
![]() $v\in U$
satisfying
$v\in U$
satisfying
![]() $|(R\cap N(v))\setminus (N(v_1)\cup \cdots \cup N(v_k))|=|N(v)\cap W|\le \rho |W|$
or
$|(R\cap N(v))\setminus (N(v_1)\cup \cdots \cup N(v_k))|=|N(v)\cap W|\le \rho |W|$
or
![]() $|R\setminus (N(v_1)\cup \cdots \cup N(v_k)\cup N(v))|=|W\setminus N(v)|\le \rho |W|$
. Hence, as
$|R\setminus (N(v_1)\cup \cdots \cup N(v_k)\cup N(v))|=|W\setminus N(v)|\le \rho |W|$
. Hence, as
![]() $|U|>n^{1/5}$
, there exists a vertex
$|U|>n^{1/5}$
, there exists a vertex
![]() $v_{k+1}\in U$
with
$v_{k+1}\in U$
with
![]() $|(R\cap N(v_{k+1}))\setminus (N(v_1)\cup \cdots \cup N(v_k))|>\rho |W|\geq \rho ^{k+1}|R|$
and
$|(R\cap N(v_{k+1}))\setminus (N(v_1)\cup \cdots \cup N(v_k))|>\rho |W|\geq \rho ^{k+1}|R|$
and
![]() $|R\setminus (N(v_1)\cup \cdots \cup N(v_{k+1}))|> \rho |W|\geq \rho ^{k+1}|R|$
. So we can indeed construct a q-tuple
$|R\setminus (N(v_1)\cup \cdots \cup N(v_{k+1}))|> \rho |W|\geq \rho ^{k+1}|R|$
. So we can indeed construct a q-tuple
![]() $(v_{1},\ldots ,v_{q})\in U^q$
satisfying (8.3) for
$(v_{1},\ldots ,v_{q})\in U^q$
satisfying (8.3) for
![]() $r=1,\ldots ,q$
.
$r=1,\ldots ,q$
.
By repeatedly applying the above claim, we can now greedily construct a collection
![]() $\mathcal {V}\subseteq R^q$
of
$\mathcal {V}\subseteq R^q$
of
![]() $\lceil n^{1-\beta }\rceil $
disjoint q-tuples of vertices in R such that each such q-tuple
$\lceil n^{1-\beta }\rceil $
disjoint q-tuples of vertices in R such that each such q-tuple
![]() $(v_1,\ldots ,v_q)\in \mathcal {V}$
satisfies (8.3) for
$(v_1,\ldots ,v_q)\in \mathcal {V}$
satisfies (8.3) for
![]() $r=1,\ldots ,q$
(indeed, as long as our collection
$r=1,\ldots ,q$
(indeed, as long as our collection
![]() $\mathcal {V}$
has size
$\mathcal {V}$
has size
![]() $|\mathcal {V}|<n^{1-\beta }$
, the number of vertices appearing in some q-tuple in
$|\mathcal {V}|<n^{1-\beta }$
, the number of vertices appearing in some q-tuple in
![]() $\mathcal {V}$
is at most
$\mathcal {V}$
is at most
![]() $q\cdot n^{1-\beta }<(\zeta \log n)\cdot n^{1-\beta }<n^{1-\beta /2}/2\leq |R|/2$
, and hence there are at least
$q\cdot n^{1-\beta }<(\zeta \log n)\cdot n^{1-\beta }<n^{1-\beta /2}/2\leq |R|/2$
, and hence there are at least
![]() $|R|/2>n^{1/5}$
vertices in R remaining). Now, define I to be the set of the
$|R|/2>n^{1/5}$
vertices in R remaining). Now, define I to be the set of the
![]() $q\cdot \lceil n^{1-\beta }\rceil \le (\zeta \log n)\cdot 2n^{1-\beta }\le n^{1-\beta (1+\rho )/2}/2$
vertices appearing in the q-tuples in
$q\cdot \lceil n^{1-\beta }\rceil \le (\zeta \log n)\cdot 2n^{1-\beta }\le n^{1-\beta (1+\rho )/2}/2$
vertices appearing in the q-tuples in
![]() $\mathcal {V}$
, and let
$\mathcal {V}$
, and let
![]() $J=V(G)\setminus I$
. We claim that now for every
$J=V(G)\setminus I$
. We claim that now for every
![]() $(v_1,\ldots ,v_q)\in \mathcal {V}$
and every
$(v_1,\ldots ,v_q)\in \mathcal {V}$
and every
![]() $r=1,\ldots ,q$
the desired conditions in (8.2) follows from (8.3). Indeed, by (8.3) the sets appearing in (8.2) have size at least
$r=1,\ldots ,q$
the desired conditions in (8.2) follows from (8.3). Indeed, by (8.3) the sets appearing in (8.2) have size at least
![]() $\rho ^r|R|-|R\cap I|\geq \rho ^q\cdot n^{1-\beta /2}-|I|\geq n^{-\beta \rho /2}\cdot n^{1-\beta /2}-n^{1-\beta (1+\rho )/2}/2=n^{1-\beta (1+\rho )/2}/2\geq n^{1-\beta }$
(using that
$\rho ^r|R|-|R\cap I|\geq \rho ^q\cdot n^{1-\beta /2}-|I|\geq n^{-\beta \rho /2}\cdot n^{1-\beta /2}-n^{1-\beta (1+\rho )/2}/2=n^{1-\beta (1+\rho )/2}/2\geq n^{1-\beta }$
(using that
![]() $\rho <1$
and n is sufficiently large).
$\rho <1$
and n is sufficiently large).
Roughly speaking, the condition in (8.2) states that
![]() $(v_1,\ldots ,v_q)$
have very different neighborhoods. This allows us to obtain strong joint probability bounds on degree statistics, as follows.
$(v_1,\ldots ,v_q)$
have very different neighborhoods. This allows us to obtain strong joint probability bounds on degree statistics, as follows.
Lemma 8.3. Fix
![]() $\eta>0$
. In an n-vertex graph G, let
$\eta>0$
. In an n-vertex graph G, let
![]() $(v_{1},\ldots ,v_{q})$
be a tuple of vertices satisfying (8.2) (for all
$(v_{1},\ldots ,v_{q})$
be a tuple of vertices satisfying (8.2) (for all
![]() $r=1,\ldots ,q$
) for some vertex subset
$r=1,\ldots ,q$
) for some vertex subset
![]() $J\subseteq V(G)$
and some
$J\subseteq V(G)$
and some
![]() $0<\beta <1$
. For some
$0<\beta <1$
. For some
![]() $\ell \in \mathbb N$
with
$\ell \in \mathbb N$
with
![]() $\eta n\le \ell \le (1-\eta )n$
, let U be a random subset of
$\eta n\le \ell \le (1-\eta )n$
, let U be a random subset of
![]() $\ell $
vertices of G. Consider any
$\ell $
vertices of G. Consider any
![]() $\tau \in \mathbb {R}\setminus \{0\}$
, any
$\tau \in \mathbb {R}\setminus \{0\}$
, any
![]() $0<\delta \leq 1/2$
, and
$0<\delta \leq 1/2$
, and
![]() $\vec {x}\in \mathbb {R}^{q}$
. Then
$\vec {x}\in \mathbb {R}^{q}$
. Then
 $$ \begin{align*}&\Pr\left[\left\Vert\tau\deg_{U\cap J}(v_{r})-\tau\deg_{U\cap J}(v_{1})+x_{r}\right\Vert{}_{\mathbb{R}/\mathbb Z}<\delta\text{ for }r=2,\ldots,q\right]\\ &\qquad\qquad\le\left(O_{\eta}\left(\frac{(|\tau|+\delta) (|\tau|+n^{-(1-\beta)/2})}{|\tau|}\right)\right)^{q-1}.\end{align*} $$
$$ \begin{align*}&\Pr\left[\left\Vert\tau\deg_{U\cap J}(v_{r})-\tau\deg_{U\cap J}(v_{1})+x_{r}\right\Vert{}_{\mathbb{R}/\mathbb Z}<\delta\text{ for }r=2,\ldots,q\right]\\ &\qquad\qquad\le\left(O_{\eta}\left(\frac{(|\tau|+\delta) (|\tau|+n^{-(1-\beta)/2})}{|\tau|}\right)\right)^{q-1}.\end{align*} $$
To prove Lemma 8.3, we will need the following estimate for hypergeometric distributions.
Lemma 8.4. Fix
![]() $\eta>0$
. For some even positive integer k, let
$\eta>0$
. For some even positive integer k, let
![]() $Z\sim \mathrm {Hyp}(k,k/2,\ell )$
with
$Z\sim \mathrm {Hyp}(k,k/2,\ell )$
with
![]() $\eta k\le \ell \le (1-\eta )k$
. Then for any
$\eta k\le \ell \le (1-\eta )k$
. Then for any
![]() $\tau \in \mathbb {R}\setminus \{0\}$
, any
$\tau \in \mathbb {R}\setminus \{0\}$
, any
![]() $0<\delta \leq 1/2$
and
$0<\delta \leq 1/2$
and
![]() $x\in \mathbb {R}$
, we have
$x\in \mathbb {R}$
, we have
 $$\begin{align*}\Pr\left[\left\Vert\tau Z+x\right\Vert{}_{\mathbb{R}/\mathbb Z}\le\delta\right]\lesssim_{\eta}\frac{(|\tau|+\delta) (|\tau|+1/\sqrt{k})}{|\tau|}.\end{align*}$$
$$\begin{align*}\Pr\left[\left\Vert\tau Z+x\right\Vert{}_{\mathbb{R}/\mathbb Z}\le\delta\right]\lesssim_{\eta}\frac{(|\tau|+\delta) (|\tau|+1/\sqrt{k})}{|\tau|}.\end{align*}$$
Proof. We may assume that
![]() $x\in [-\tau \mathbb {E}Z, -\tau \mathbb {E}Z +1]$
, which implies that
$x\in [-\tau \mathbb {E}Z, -\tau \mathbb {E}Z +1]$
, which implies that
![]() $x/\tau $
differs from
$x/\tau $
differs from
![]() $-\mathbb {E}Z$
by at most
$-\mathbb {E}Z$
by at most
![]() $1/|\tau |$
. Note that the standard deviation of Z is
$1/|\tau |$
. Note that the standard deviation of Z is
![]() $\Theta _{\eta }(\sqrt {k})$
; by direct computation or a nonuniform quantitative central limit theorem for the hypergeometric distribution (for example, [Reference Lahiri, Chatterjee and Maiti69, Theorem 2.3]), for any
$\Theta _{\eta }(\sqrt {k})$
; by direct computation or a nonuniform quantitative central limit theorem for the hypergeometric distribution (for example, [Reference Lahiri, Chatterjee and Maiti69, Theorem 2.3]), for any
![]() $y\in \mathbb {R}$
we have
$y\in \mathbb {R}$
we have
 $$\begin{align*}\Pr[Z-\mathbb E Z=y]\lesssim_{\eta} \frac{\exp\left(-\Omega_{\eta}(y^2/k)\right)}{\sqrt{k}}. \end{align*}$$
$$\begin{align*}\Pr[Z-\mathbb E Z=y]\lesssim_{\eta} \frac{\exp\left(-\Omega_{\eta}(y^2/k)\right)}{\sqrt{k}}. \end{align*}$$
It follows that
 $$ \begin{align*} \Pr\left[\left\Vert\tau Z+x\right\Vert{}_{\mathbb{R}/\mathbb Z}\le\delta\right] &\le\sum_{i\in\mathbb Z}\Pr\left[\left|Z+\frac{x}{\tau}-\frac{i}{\tau}\right| \le \frac{\delta}{|\tau|}\right]\\ &\lesssim_{\eta} \sum_{i\in\mathbb Z} \sum_{\substack{j\in\mathbb{Z}\\|j+x/\tau-i/\tau|\leq \delta/|\tau|}} \!\!\!\!\!\!\!\frac{\exp\left(-\Omega_{\eta}((j-\mathbb EZ)^2/k)\right)}{\sqrt{k}}\\ &\lesssim_{\eta}\sum_{i\in\mathbb Z}\left(1+2\frac{\delta}{|\tau|}\right)\frac{\exp\left(-\Omega_{\eta}\left((\max\{0,|i/\tau|-(1+\delta)/|\tau|\})^2/k\right)\right)}{\sqrt{k}}\\ &\le \left(1+2\frac{\delta}{|\tau|}\right)\left(\sum_{\substack{i\in\mathbb Z\\|i|>4}}\frac{\exp\left(-\Omega_{\eta}\left(i^2/(4\tau^2k)\right)\right)}{\sqrt{k}}+\sum_{\substack{i\in\mathbb Z\\|i| \le 4}}\frac{1}{\sqrt{k}}\right)\\ &\lesssim_{\eta} \frac{|\tau|+\delta}{|\tau|}\cdot \left(\frac{|\tau|\sqrt{k}}{\sqrt{k}}+\frac{1}{\sqrt{k}}\right)=\frac{(|\tau|+\delta) (|\tau|+1/\sqrt{k})}{|\tau|}, \end{align*} $$
$$ \begin{align*} \Pr\left[\left\Vert\tau Z+x\right\Vert{}_{\mathbb{R}/\mathbb Z}\le\delta\right] &\le\sum_{i\in\mathbb Z}\Pr\left[\left|Z+\frac{x}{\tau}-\frac{i}{\tau}\right| \le \frac{\delta}{|\tau|}\right]\\ &\lesssim_{\eta} \sum_{i\in\mathbb Z} \sum_{\substack{j\in\mathbb{Z}\\|j+x/\tau-i/\tau|\leq \delta/|\tau|}} \!\!\!\!\!\!\!\frac{\exp\left(-\Omega_{\eta}((j-\mathbb EZ)^2/k)\right)}{\sqrt{k}}\\ &\lesssim_{\eta}\sum_{i\in\mathbb Z}\left(1+2\frac{\delta}{|\tau|}\right)\frac{\exp\left(-\Omega_{\eta}\left((\max\{0,|i/\tau|-(1+\delta)/|\tau|\})^2/k\right)\right)}{\sqrt{k}}\\ &\le \left(1+2\frac{\delta}{|\tau|}\right)\left(\sum_{\substack{i\in\mathbb Z\\|i|>4}}\frac{\exp\left(-\Omega_{\eta}\left(i^2/(4\tau^2k)\right)\right)}{\sqrt{k}}+\sum_{\substack{i\in\mathbb Z\\|i| \le 4}}\frac{1}{\sqrt{k}}\right)\\ &\lesssim_{\eta} \frac{|\tau|+\delta}{|\tau|}\cdot \left(\frac{|\tau|\sqrt{k}}{\sqrt{k}}+\frac{1}{\sqrt{k}}\right)=\frac{(|\tau|+\delta) (|\tau|+1/\sqrt{k})}{|\tau|}, \end{align*} $$
where in the third step we used that for any
![]() $i\in \mathbb Z$
there are at most
$i\in \mathbb Z$
there are at most
![]() $1+2\delta /|\tau |$
integers
$1+2\delta /|\tau |$
integers
![]() $j\in \mathbb Z$
satisfying
$j\in \mathbb Z$
satisfying
![]() $|j+x/\tau -i/\tau |\leq \delta /|\tau |$
, and for every such integer we have
$|j+x/\tau -i/\tau |\leq \delta /|\tau |$
, and for every such integer we have
![]() $|j-\mathbb EZ|\geq |i|/\tau -1/|\tau |-\delta /|\tau |$
(since
$|j-\mathbb EZ|\geq |i|/\tau -1/|\tau |-\delta /|\tau |$
(since
![]() $x/\tau $
differs from
$x/\tau $
differs from
![]() $-\mathbb {E}Z$
by at most
$-\mathbb {E}Z$
by at most
![]() $1/|\tau |$
).
$1/|\tau |$
).
From this, we deduce Lemma 8.3.
Proof of Lemma 8.3
For
![]() $r=2,\ldots ,q$
, let
$r=2,\ldots ,q$
, let
![]() $\mathcal {E}_{r}$
be the event that
$\mathcal {E}_{r}$
be the event that
![]() $\|\tau \deg _{U\cap J}(v_{i})-\tau \deg _{U\cap J}(v_{1})+x_{i}\|_{\mathbb {R}/\mathbb Z}<\delta $
. We claim that
$\|\tau \deg _{U\cap J}(v_{i})-\tau \deg _{U\cap J}(v_{1})+x_{i}\|_{\mathbb {R}/\mathbb Z}<\delta $
. We claim that
 $$\begin{align*}\Pr[\mathcal{E}_{r}\,|\,\mathcal{E}_{2}\cap\cdots\cap\mathcal{E}_{r-1}]\lesssim_{\eta}\frac{(|\tau|+\delta) (|\tau|+n^{-(1-\beta)/2})}{|\tau|}.\end{align*}$$
$$\begin{align*}\Pr[\mathcal{E}_{r}\,|\,\mathcal{E}_{2}\cap\cdots\cap\mathcal{E}_{r-1}]\lesssim_{\eta}\frac{(|\tau|+\delta) (|\tau|+n^{-(1-\beta)/2})}{|\tau|}.\end{align*}$$
for every
![]() $r=2,\ldots ,q$
. This will suffice, since the desired probability in the statement of Lemma 8.3 is
$r=2,\ldots ,q$
. This will suffice, since the desired probability in the statement of Lemma 8.3 is
 $$\begin{align*}\Pr[\mathcal{E}_{2}\cap\cdots\cap\mathcal{E}_{q}]=\prod_{r=2}^{q}\Pr[\mathcal{E}_{r}\,|\,\mathcal{E}_{2}\cap\cdots\cap\mathcal{E}_{r-1}].\end{align*}$$
$$\begin{align*}\Pr[\mathcal{E}_{2}\cap\cdots\cap\mathcal{E}_{q}]=\prod_{r=2}^{q}\Pr[\mathcal{E}_{r}\,|\,\mathcal{E}_{2}\cap\cdots\cap\mathcal{E}_{r-1}].\end{align*}$$
Now, fix
![]() $r\in \{2,\ldots ,q\}$
. By assumption both of the sets appearing in condition (8.2) have size at least
$r\in \{2,\ldots ,q\}$
. By assumption both of the sets appearing in condition (8.2) have size at least
![]() $\lceil n^{1-\beta }\rceil $
. Inside each of these two sets, we choose some subset of size exactly
$\lceil n^{1-\beta }\rceil $
. Inside each of these two sets, we choose some subset of size exactly
![]() $\lceil n^{1-\beta }\rceil $
and we define
$\lceil n^{1-\beta }\rceil $
and we define
![]() $S\subseteq J\setminus (N(v_1)\cup \cdots \cup N(v_{r-1}))$
to be the union of these two subsets. Then
$S\subseteq J\setminus (N(v_1)\cup \cdots \cup N(v_{r-1}))$
to be the union of these two subsets. Then
![]() $|S|=2\lceil n^{1-\beta }\rceil $
and
$|S|=2\lceil n^{1-\beta }\rceil $
and
![]() $|S\cap N(v_r)|=\lceil n^{1-\beta }\rceil $
. For the random set
$|S\cap N(v_r)|=\lceil n^{1-\beta }\rceil $
. For the random set
![]() $U\subseteq V(G)$
of size
$U\subseteq V(G)$
of size
![]() $\ell $
, let us now condition on an outcome of
$\ell $
, let us now condition on an outcome of
![]() $|U\cap S|$
such that
$|U\cap S|$
such that
![]() $(\eta /2)|S|\le |U\cap S|\le (1-\eta /2)|S|$
(by a Chernoff bound for hypergeometric random variables, as in Lemma 4.16, this happens with probability
$(\eta /2)|S|\le |U\cap S|\le (1-\eta /2)|S|$
(by a Chernoff bound for hypergeometric random variables, as in Lemma 4.16, this happens with probability
![]() $1-n^{-\omega _{\eta }(1)}\geq 1- ((|\tau |+\delta )/|\tau |)\cdot n^{-(1-\beta )/2}$
), and condition on any outcome of
$1-n^{-\omega _{\eta }(1)}\geq 1- ((|\tau |+\delta )/|\tau |)\cdot n^{-(1-\beta )/2}$
), and condition on any outcome of
![]() $U\setminus S$
(as S is disjoint from
$U\setminus S$
(as S is disjoint from
![]() $N(v_1)\cup \cdots \cup N(v_{r-1})$
, this determines the value of
$N(v_1)\cup \cdots \cup N(v_{r-1})$
, this determines the value of
![]() $\deg _{U\cap J}(v_{j})$
for
$\deg _{U\cap J}(v_{j})$
for
![]() $j=1,\ldots ,r-1$
and in particular determines whether the events
$j=1,\ldots ,r-1$
and in particular determines whether the events
![]() $\mathcal {E}_{j}$
hold for
$\mathcal {E}_{j}$
hold for
![]() $j=2,\ldots ,r-1$
). Now, conditionally,
$j=2,\ldots ,r-1$
). Now, conditionally,
![]() $\deg _{ U\cap S}(v_{r})=|U\cap S\cap N(v_r)|$
has a hypergeometric distribution
$\deg _{ U\cap S}(v_{r})=|U\cap S\cap N(v_r)|$
has a hypergeometric distribution
![]() $\mathrm {Hyp}(|S|,|S|/2,|U\cap S|)$
, so the claim follows from Lemma 8.4 (taking
$\mathrm {Hyp}(|S|,|S|/2,|U\cap S|)$
, so the claim follows from Lemma 8.4 (taking
![]() $x=\tau \deg _{(U\cap J)\setminus S}(v_{1})-\tau \deg _{U\cap J}(v_{1})+x_{r}$
), recalling that
$x=\tau \deg _{(U\cap J)\setminus S}(v_{1})-\tau \deg _{U\cap J}(v_{1})+x_{r}$
), recalling that
![]() $|S|=2\lceil n^{1-\beta }\rceil $
.
$|S|=2\lceil n^{1-\beta }\rceil $
.
We are now ready to prove Lemma 8.1.
Proof of Lemma 8.1
We apply Lemma 8.2 with
![]() $\beta =\eta /3$
, obtaining a partition
$\beta =\eta /3$
, obtaining a partition
![]() $V(G)=I\cup J$
and a collection
$V(G)=I\cup J$
and a collection
![]() $\mathcal {V}\subseteq I^q$
of at least
$\mathcal {V}\subseteq I^q$
of at least
![]() $n^{1-\eta /3}$
disjoint q-tuples of vertices in I, where
$n^{1-\eta /3}$
disjoint q-tuples of vertices in I, where
![]() $q=\lfloor \zeta \log n\rfloor $
with
$q=\lfloor \zeta \log n\rfloor $
with
![]() $\zeta =\zeta (C,\eta /3)>0$
, such that each q-tuple
$\zeta =\zeta (C,\eta /3)>0$
, such that each q-tuple
![]() $(v_1,\ldots ,v_q)\in \mathcal {V}$
satisfies (8.2) for
$(v_1,\ldots ,v_q)\in \mathcal {V}$
satisfies (8.2) for
![]() $r=1,\ldots ,q$
. Let A denote the adjacency matrix of G, and let
$r=1,\ldots ,q$
. Let A denote the adjacency matrix of G, and let
![]() $\vec \xi \in \{0,1\}^n$
be the characteristic vector of the random set U (meaning
$\vec \xi \in \{0,1\}^n$
be the characteristic vector of the random set U (meaning
![]() $\vec {\xi }_v=1$
if
$\vec {\xi }_v=1$
if
![]() $v\in U$
, and
$v\in U$
, and
![]() $\vec {\xi }_v=0$
if
$\vec {\xi }_v=0$
if
![]() $v\notin U$
), so
$v\notin U$
), so
![]() $\vec \xi \in \{0,1\}^n$
is a uniformly random vector with precisely
$\vec \xi \in \{0,1\}^n$
is a uniformly random vector with precisely
![]() $\ell $
ones. We define
$\ell $
ones. We define
 $$\begin{align*}f(\vec{\xi}):=X=e(G[U])+\sum_{v\in U}e_v+e_0=\frac{1}{2}\vec{\xi}^{\intercal}A\vec{\xi}+\vec{e}\cdot\vec{\xi}+e_0.\end{align*}$$
$$\begin{align*}f(\vec{\xi}):=X=e(G[U])+\sum_{v\in U}e_v+e_0=\frac{1}{2}\vec{\xi}^{\intercal}A\vec{\xi}+\vec{e}\cdot\vec{\xi}+e_0.\end{align*}$$
For the rest of the proof, we condition on an outcome of
![]() $|U\cap I|$
satisfying
$|U\cap I|$
satisfying
![]() $(\eta /2)|I|\le |U\cap I|\le (1-\eta /2)|I|$
. By a Chernoff bound for hypergeometric random variables, as in Lemma 4.16, this occurs with probability
$(\eta /2)|I|\le |U\cap I|\le (1-\eta /2)|I|$
. By a Chernoff bound for hypergeometric random variables, as in Lemma 4.16, this occurs with probability
![]() $1-n^{-\omega _{\eta }(1)}$
(as
$1-n^{-\omega _{\eta }(1)}$
(as
![]() $\eta n\leq \ell \leq (1-\eta )n$
and
$\eta n\leq \ell \leq (1-\eta )n$
and
![]() $|I|\geq n^{1-\eta /3}$
), so the characteristic function for the random variable X under this conditioning differs from the original characteristic function
$|I|\geq n^{1-\eta /3}$
), so the characteristic function for the random variable X under this conditioning differs from the original characteristic function
![]() $\varphi _X$
by at most
$\varphi _X$
by at most
![]() $n^{-\omega _{\eta }(1)}$
. Hence, it suffices to prove that
$n^{-\omega _{\eta }(1)}$
. Hence, it suffices to prove that
![]() $|\varphi _X(\tau )|\le n^{-6}$
(for
$|\varphi _X(\tau )|\le n^{-6}$
(for
![]() $n^{-1+\eta }\le |\tau |\le \nu $
) for our conditional random variable X.
$n^{-1+\eta }\le |\tau |\le \nu $
) for our conditional random variable X.
Let
![]() $\vec \xi _I$
and
$\vec \xi _I$
and
![]() $\vec \xi _J$
be the restrictions of
$\vec \xi _J$
be the restrictions of
![]() $\vec \xi $
to the index sets I and J. Having conditioned on
$\vec \xi $
to the index sets I and J. Having conditioned on
![]() $|U\cap I|$
, these vectors
$|U\cap I|$
, these vectors
![]() $\vec {\xi }_{I}$
and
$\vec {\xi }_{I}$
and
![]() $\vec {\xi }_{J}$
are independent from each other. Let
$\vec {\xi }_{J}$
are independent from each other. Let
![]() $\vec {\xi }_{J}'$
be an independent copy of
$\vec {\xi }_{J}'$
be an independent copy of
![]() $\vec {\xi }_{J}$
; by (8.1), we have
$\vec {\xi }_{J}$
; by (8.1), we have
Now, we can write
![]() $f(\vec {\xi }_{I},\vec {\xi }_{J})-f(\vec {\xi }_{I},\vec {\xi }_{J}')=\sum _{i\in I}a_{i}\xi _{i}+b$
, where
$f(\vec {\xi }_{I},\vec {\xi }_{J})-f(\vec {\xi }_{I},\vec {\xi }_{J}')=\sum _{i\in I}a_{i}\xi _{i}+b$
, where
![]() $a_{i}=\sum _{j\in J}A_{i,j}(\xi _{j}-\xi _{j}')$
for each
$a_{i}=\sum _{j\in J}A_{i,j}(\xi _{j}-\xi _{j}')$
for each
![]() $i\in I$
and b only depends on
$i\in I$
and b only depends on
![]() $\vec {\xi }_{J}$
and
$\vec {\xi }_{J}$
and
![]() $\vec {\xi }_{J}'$
(but not on
$\vec {\xi }_{J}'$
(but not on
![]() $\vec {\xi }_{I}$
). Let
$\vec {\xi }_{I}$
). Let
![]() $\delta =n^{-1/2+\eta /3}$
.
$\delta =n^{-1/2+\eta /3}$
.
Claim 8.5. With probability at least
![]() $1-n^{-12}/2$
the outcome of
$1-n^{-12}/2$
the outcome of
![]() $(\vec {\xi }_{J},\vec {\xi }_{J}')$
is such that
$(\vec {\xi }_{J},\vec {\xi }_{J}')$
is such that
for at least
![]() $\left |\mathcal {V}\right |/2\geq n^{1-\eta /3}/2$
disjoint pairs
$\left |\mathcal {V}\right |/2\geq n^{1-\eta /3}/2$
disjoint pairs
![]() $(i,i')\in I^{2}$
.
$(i,i')\in I^{2}$
.
Assuming Claim 8.5, it follows from Lemma 4.8 that with probability at least
![]() $1-n^{-12}/2$
, the outcome of
$1-n^{-12}/2$
, the outcome of
![]() $\vec {\xi }_{J}$
and
$\vec {\xi }_{J}$
and
![]() $\vec {\xi }_{J}'$
is such that
$\vec {\xi }_{J}'$
is such that
 $$ \begin{align*} \left|\mathbb E[e^{i\tau(f(\vec{\xi}_{I},\vec{\xi}_{J})-f(\vec{\xi}_{I},\vec{\xi}_{J}'))}\mid\vec{\xi}_{J},\vec{\xi}_{J}']\right|&=\left|\mathbb E[e^{i\tau\left(\sum_{i\in I} a_i\xi_i+b\right)}\mid\vec{\xi}_{J},\vec{\xi}_{J}']\right|\\ &=\left|\mathbb E[e^{i\sum_{i\in I} \tau a_i\xi_i}\mid\vec{\xi}_{J},\vec{\xi}_{J}']\right|\lesssim e^{-\Omega_{\eta}(n^{\eta/3})}. \end{align*} $$
$$ \begin{align*} \left|\mathbb E[e^{i\tau(f(\vec{\xi}_{I},\vec{\xi}_{J})-f(\vec{\xi}_{I},\vec{\xi}_{J}'))}\mid\vec{\xi}_{J},\vec{\xi}_{J}']\right|&=\left|\mathbb E[e^{i\tau\left(\sum_{i\in I} a_i\xi_i+b\right)}\mid\vec{\xi}_{J},\vec{\xi}_{J}']\right|\\ &=\left|\mathbb E[e^{i\sum_{i\in I} \tau a_i\xi_i}\mid\vec{\xi}_{J},\vec{\xi}_{J}']\right|\lesssim e^{-\Omega_{\eta}(n^{\eta/3})}. \end{align*} $$
For sufficiently large n, the right-hand side is bounded by
![]() $n^{-12}/2$
. Noting that the expectation on the left-hand side is bounded by
$n^{-12}/2$
. Noting that the expectation on the left-hand side is bounded by
![]() $1$
for all outcomes of
$1$
for all outcomes of
![]() $\vec {\xi }_{J}$
and
$\vec {\xi }_{J}$
and
![]() $\vec {\xi }_{J}'$
, we can conclude that the right-hand side of (8.4) is bounded by
$\vec {\xi }_{J}'$
, we can conclude that the right-hand side of (8.4) is bounded by
![]() $n^{-12}$
and therefore
$n^{-12}$
and therefore
![]() $|\varphi _{X}(\tau )|\leq n^{-6}$
for sufficiently large n, as desired. It remains to prove Claim 8.5.
$|\varphi _{X}(\tau )|\leq n^{-6}$
for sufficiently large n, as desired. It remains to prove Claim 8.5.
Proof of Claim 8.5
Let us also condition on any outcome of
![]() $\vec {\xi }_{J}'$
. We say that a q-tuple
$\vec {\xi }_{J}'$
. We say that a q-tuple
![]() $(v_{1},\ldots ,v_{q})\in \mathcal {V}$
is bad if no pair
$(v_{1},\ldots ,v_{q})\in \mathcal {V}$
is bad if no pair
![]() $(v_r, v_1)\in I^2$
with
$(v_r, v_1)\in I^2$
with
![]() $r\in \{2,\ldots ,q\}$
has the property in the claim. In other words,
$r\in \{2,\ldots ,q\}$
has the property in the claim. In other words,
![]() $(v_{1},\ldots ,v_{q})$
is bad if for all
$(v_{1},\ldots ,v_{q})$
is bad if for all
![]() $r=2,\ldots ,q$
we have
$r=2,\ldots ,q$
we have
![]() $\left \Vert \tau a_{v_r}/(2\pi )-\tau a_{v_1}/(2\pi )\right \Vert {}_{\mathbb {R}/\mathbb Z}<\delta $
.
$\left \Vert \tau a_{v_r}/(2\pi )-\tau a_{v_1}/(2\pi )\right \Vert {}_{\mathbb {R}/\mathbb Z}<\delta $
.
For any q-tuple
![]() $(v_{1},\ldots ,v_{q})\in \mathcal {V}$
, we can bound the probability that
$(v_{1},\ldots ,v_{q})\in \mathcal {V}$
, we can bound the probability that
![]() $(v_{1},\ldots ,v_{q})$
is bad by applying Lemma 8.3 with
$(v_{1},\ldots ,v_{q})$
is bad by applying Lemma 8.3 with
![]() $x_{r}=-(\tau /(2\pi ))\sum _{j\in J}(A_{v_r,j}-A_{v_1,j})\xi _{j}'$
for
$x_{r}=-(\tau /(2\pi ))\sum _{j\in J}(A_{v_r,j}-A_{v_1,j})\xi _{j}'$
for
![]() $r=2,\ldots ,q$
(recall that
$r=2,\ldots ,q$
(recall that
![]() $(v_{1},\ldots ,v_{q})$
satisfies (8.2)), obtaining
$(v_{1},\ldots ,v_{q})$
satisfies (8.2)), obtaining
 $$ \begin{align*} &\Pr[(v_{1},\ldots,v_{q})\text{ is bad}] \\ &\qquad=\Pr\left[\left\Vert\tau a_{v_r}/(2\pi)-\tau a_{v_1}/(2\pi)\right\Vert{}_{\mathbb{R}/\mathbb Z}<\delta\text{ for }r=2,\ldots,q\right]\\ &\qquad =\Pr\left[\left\Vert(\tau/(2\pi))\deg_{U\cap J}(v_{r})-(\tau/(2\pi))\deg_{U\cap J}(v_{1})+x_{r}\right\Vert{}_{\mathbb{R}/\mathbb Z}<\delta\text{ for }r=2,\ldots,q\right]\\ &\qquad \le\left(O_{\eta}\left(\frac{(|\tau/(2\pi)|+\delta) (|\tau/(2\pi)|+n^{-(1-\beta)/2})}{|\tau/(2\pi)|}\right)\right)^{q-1}\\ &\qquad\le\left(O_{\eta}\left(\frac{(|\tau|+n^{-1/2+\eta/3}) (|\tau|+n^{-1/2+\eta/6})}{|\tau|}\right)\right)^{q-1}\le \left(O_{\eta}(\nu+n^{-\eta/2})\right)^{\lfloor\zeta\log n\rfloor-1}, \end{align*} $$
$$ \begin{align*} &\Pr[(v_{1},\ldots,v_{q})\text{ is bad}] \\ &\qquad=\Pr\left[\left\Vert\tau a_{v_r}/(2\pi)-\tau a_{v_1}/(2\pi)\right\Vert{}_{\mathbb{R}/\mathbb Z}<\delta\text{ for }r=2,\ldots,q\right]\\ &\qquad =\Pr\left[\left\Vert(\tau/(2\pi))\deg_{U\cap J}(v_{r})-(\tau/(2\pi))\deg_{U\cap J}(v_{1})+x_{r}\right\Vert{}_{\mathbb{R}/\mathbb Z}<\delta\text{ for }r=2,\ldots,q\right]\\ &\qquad \le\left(O_{\eta}\left(\frac{(|\tau/(2\pi)|+\delta) (|\tau/(2\pi)|+n^{-(1-\beta)/2})}{|\tau/(2\pi)|}\right)\right)^{q-1}\\ &\qquad\le\left(O_{\eta}\left(\frac{(|\tau|+n^{-1/2+\eta/3}) (|\tau|+n^{-1/2+\eta/6})}{|\tau|}\right)\right)^{q-1}\le \left(O_{\eta}(\nu+n^{-\eta/2})\right)^{\lfloor\zeta\log n\rfloor-1}, \end{align*} $$
using that
![]() $n^{-1+\eta }\le |\tau |\le \nu $
. Now, if
$n^{-1+\eta }\le |\tau |\le \nu $
. Now, if
![]() $\nu $
is sufficiently small with respect to C and
$\nu $
is sufficiently small with respect to C and
![]() $\eta $
(and consequently also sufficiently small with respect to
$\eta $
(and consequently also sufficiently small with respect to
![]() $\zeta $
), we deduce that
$\zeta $
), we deduce that
![]() $\Pr [(v_{1},\ldots ,v_{q})\text { is bad}]\leq 1/(4n^{12})$
. Hence, the expected number of bad tuples
$\Pr [(v_{1},\ldots ,v_{q})\text { is bad}]\leq 1/(4n^{12})$
. Hence, the expected number of bad tuples
![]() $(v_{1},\ldots ,v_{q})\in \mathcal {V}$
is at most
$(v_{1},\ldots ,v_{q})\in \mathcal {V}$
is at most
![]() $|\mathcal {V}|/(4n^{12})$
. Thus, by Markov’s inequality, with probability at least
$|\mathcal {V}|/(4n^{12})$
. Thus, by Markov’s inequality, with probability at least
![]() $1-n^{-12}/2$
there are at most
$1-n^{-12}/2$
there are at most
![]() $|\mathcal {V}|/2$
bad q-tuples in
$|\mathcal {V}|/2$
bad q-tuples in
![]() $\mathcal {V}$
. When this is the case, among each of the at least
$\mathcal {V}$
. When this is the case, among each of the at least
![]() $|\mathcal {V}|/2$
different q-tuples
$|\mathcal {V}|/2$
different q-tuples
![]() $(v_{1},\ldots ,v_{q})\in \mathcal {V}$
that are not bad we can find a pair
$(v_{1},\ldots ,v_{q})\in \mathcal {V}$
that are not bad we can find a pair
![]() $(v_r, v_1)\in I^2$
with the desired property that
$(v_r, v_1)\in I^2$
with the desired property that
![]() $\left \Vert \tau a_{v_r}/(2\pi )-\tau a_{v_1}/(2\pi )\right \Vert {}_{\mathbb {R}/\mathbb Z}\geq \delta $
. Since the q-tuples in
$\left \Vert \tau a_{v_r}/(2\pi )-\tau a_{v_1}/(2\pi )\right \Vert {}_{\mathbb {R}/\mathbb Z}\geq \delta $
. Since the q-tuples in
![]() $\mathcal {V}$
are all disjoint, this gives at least
$\mathcal {V}$
are all disjoint, this gives at least
![]() $|\mathcal {V}|/2$
disjoint pairs in
$|\mathcal {V}|/2$
disjoint pairs in
![]() $I^2$
with this property, thus proving the claim.
$I^2$
with this property, thus proving the claim.
As we saw earlier, this finishes the proof of Lemma 8.1.
9 Short interval control in the additively unstructured case
Now, we can combine the characteristic function estimates in Sections 7 and 8 to prove Theorem 3.1 in the ‘additively unstructured’ case (recall the outline in Section 3.2), defined as follows. This definition is chosen so that the term
![]() $\widehat {D}_{L,\gamma }(\vec {d})$
appearing in Lemma 7.2 is large, meaning that Lemma 7.2 can be applied to a wide range of
$\widehat {D}_{L,\gamma }(\vec {d})$
appearing in Lemma 7.2 is large, meaning that Lemma 7.2 can be applied to a wide range of
![]() $|t|$
.
$|t|$
.
Definition 9.1. Fix
![]() $0<\gamma <1/4$
, consider a graph G with n vertices and a vector
$0<\gamma <1/4$
, consider a graph G with n vertices and a vector
![]() $\vec e\in \mathbb {R}_{\ge 0}^{V(G)}$
and let
$\vec e\in \mathbb {R}_{\ge 0}^{V(G)}$
and let
![]() $d_v=e_v+\deg _G(v)/2$
for all
$d_v=e_v+\deg _G(v)/2$
for all
![]() $v \in V(G)$
. Say that
$v \in V(G)$
. Say that
![]() $(G,\vec e)$
is
$(G,\vec e)$
is
![]() $\gamma $
-unstructured if
$\gamma $
-unstructured if
![]() $\widehat {D}_{L,\gamma }(\vec {d})\ge n^{1/2}$
, for
$\widehat {D}_{L,\gamma }(\vec {d})\ge n^{1/2}$
, for
![]() $L=\lceil 100/\gamma \rceil $
. Otherwise,
$L=\lceil 100/\gamma \rceil $
. Otherwise,
![]() $(G,\vec e)$
is
$(G,\vec e)$
is
![]() $\gamma $
-structured.
$\gamma $
-structured.
From now on, we fix
![]() $\gamma =10^{-4}$
. For our proof of Theorem 3.1, we split into two cases, depending on whether
$\gamma =10^{-4}$
. For our proof of Theorem 3.1, we split into two cases, depending on whether
![]() $(G,\vec e)$
is
$(G,\vec e)$
is
![]() $\gamma $
-structured. In this section, we will prove Theorem 3.1 in the case where
$\gamma $
-structured. In this section, we will prove Theorem 3.1 in the case where
![]() $(G,\vec e)$
is
$(G,\vec e)$
is
![]() $\gamma $
-unstructured. Eventually (in Section 12), we will handle the case where
$\gamma $
-unstructured. Eventually (in Section 12), we will handle the case where
![]() $(G,\vec e)$
is
$(G,\vec e)$
is
![]() $\gamma $
-structured, that is, where
$\gamma $
-structured, that is, where
![]() $\widehat {D}_{L,\gamma }(\vec {d})< n^{1/2}$
. While the arguments in this section work for any constant
$\widehat {D}_{L,\gamma }(\vec {d})< n^{1/2}$
. While the arguments in this section work for any constant
![]() $0<\gamma <1/4$
, the proof of the
$0<\gamma <1/4$
, the proof of the
![]() $\gamma $
-structured case in Section 12 requires
$\gamma $
-structured case in Section 12 requires
![]() $\gamma $
to be sufficiently small (this is why we define
$\gamma $
to be sufficiently small (this is why we define
![]() $\gamma =10^{-4}$
).
$\gamma =10^{-4}$
).
Proof of Theorem 3.1 in the
 $\gamma $
-unstructured case
$\gamma $
-unstructured case
Fix
![]() $C,H>0$
, let G and
$C,H>0$
, let G and
![]() $\vec {e}\in \mathbb {R}^{V(G)}$
and
$\vec {e}\in \mathbb {R}^{V(G)}$
and
![]() $e_0\in \mathbb {R}$
be as in Theorem 3.1 and assume that
$e_0\in \mathbb {R}$
be as in Theorem 3.1 and assume that
![]() $(G,\vec e)$
is
$(G,\vec e)$
is
![]() $\gamma $
-unstructured and that n is sufficiently large with respect to C and H. Recall that U is a uniformly random subset of
$\gamma $
-unstructured and that n is sufficiently large with respect to C and H. Recall that U is a uniformly random subset of
![]() $V(G)$
and
$V(G)$
and
![]() $X=e(G[U])+\sum _{v\in U} e_v+e_0$
, and also recall (e.g., from the proof of Lemma 7.2) that
$X=e(G[U])+\sum _{v\in U} e_v+e_0$
, and also recall (e.g., from the proof of Lemma 7.2) that
![]() $\sigma (X)=\Theta _{C,H}(n^{3/2})$
. Let
$\sigma (X)=\Theta _{C,H}(n^{3/2})$
. Let
![]() $Z\sim \mathcal {N}(\mathbb E X,\sigma (X))$
be a Gaussian random variable with the same mean and variance as X.
$Z\sim \mathcal {N}(\mathbb E X,\sigma (X))$
be a Gaussian random variable with the same mean and variance as X.
First, note that for any
![]() $\tau \in \mathbb {R}$
, Lemma 7.1 implies
$\tau \in \mathbb {R}$
, Lemma 7.1 implies
 $$ \begin{align*}|\varphi_X(\tau)-\varphi_Z(\tau)|&=\big|\varphi_{(X-\mathbb{E} X)/\sigma(X)}(\tau\sigma(X))-\varphi_{(Z-\mathbb{E} X)/\sigma(X)}(\tau\sigma(X))\big |\\ &\lesssim_{C,H}|\tau|\sigma(X)n^{-1/2}\lesssim_{C,H}|\tau|n\end{align*} $$
$$ \begin{align*}|\varphi_X(\tau)-\varphi_Z(\tau)|&=\big|\varphi_{(X-\mathbb{E} X)/\sigma(X)}(\tau\sigma(X))-\varphi_{(Z-\mathbb{E} X)/\sigma(X)}(\tau\sigma(X))\big |\\ &\lesssim_{C,H}|\tau|\sigma(X)n^{-1/2}\lesssim_{C,H}|\tau|n\end{align*} $$
(noting that the graph G has density at least
![]() $\Omega _C(1)$
by Theorem 4.1). Then, note that since
$\Omega _C(1)$
by Theorem 4.1). Then, note that since
![]() $|\varphi _Z(\tau )|=\exp (-\sigma (X)^2\tau ^2/2)$
, for
$|\varphi _Z(\tau )|=\exp (-\sigma (X)^2\tau ^2/2)$
, for
![]() $|\tau |\ge n^{2\gamma }/\sigma (X)$
we have
$|\tau |\ge n^{2\gamma }/\sigma (X)$
we have
![]() $|\varphi _Z(\tau )|\le \exp (-n^{4\gamma }/2)$
. Furthermore, in Lemma 7.2 we have
$|\varphi _Z(\tau )|\le \exp (-n^{4\gamma }/2)$
. Furthermore, in Lemma 7.2 we have
![]() $\widehat {D}_{L,\gamma }(\vec {d})\ge n^{1/2}$
by our assumption that
$\widehat {D}_{L,\gamma }(\vec {d})\ge n^{1/2}$
by our assumption that
![]() $(G,\vec e)$
is
$(G,\vec e)$
is
![]() $\gamma $
-unstructured. Hence, for
$\gamma $
-unstructured. Hence, for
![]() $\alpha =\alpha (C,H,\gamma )>0$
as in Lemma 7.2, we obtain that
$\alpha =\alpha (C,H,\gamma )>0$
as in Lemma 7.2, we obtain that
![]() $|\varphi _X(\tau )|=|\varphi _{(X-\mathbb {E} X)/\sigma (X)}(\tau \sigma (X))|\lesssim _{C,H,\gamma } n^{-5}$
for
$|\varphi _X(\tau )|=|\varphi _{(X-\mathbb {E} X)/\sigma (X)}(\tau \sigma (X))|\lesssim _{C,H,\gamma } n^{-5}$
for
![]() $n^{2\gamma }/\sigma (X)\le |\tau |\le \alpha n^{1/2+\gamma /8}/\sigma (X)$
.
$n^{2\gamma }/\sigma (X)\le |\tau |\le \alpha n^{1/2+\gamma /8}/\sigma (X)$
.
Let
![]() $\nu =\nu (C,\gamma /9)>0$
be as in Lemma 8.1. Note that by a Chernoff bound we have
$\nu =\nu (C,\gamma /9)>0$
be as in Lemma 8.1. Note that by a Chernoff bound we have
![]() $n/4\le |U|\le 3n/4$
with probability
$n/4\le |U|\le 3n/4$
with probability
![]() $1-e^{-\Omega (n)}$
. If we condition on such an outcome of
$1-e^{-\Omega (n)}$
. If we condition on such an outcome of
![]() $|U|$
, then for
$|U|$
, then for
![]() $n^{-1+\gamma /9}\le |\tau |\le \nu $
, Lemma 8.1 shows that the conditional characteristic function of X is bounded in absolute value by
$n^{-1+\gamma /9}\le |\tau |\le \nu $
, Lemma 8.1 shows that the conditional characteristic function of X is bounded in absolute value by
![]() $n^{-5}$
(assuming that n is sufficiently large). It follows that for this range of
$n^{-5}$
(assuming that n is sufficiently large). It follows that for this range of
![]() $|\tau |$
we have
$|\tau |$
we have
![]() $|\varphi _X(\tau )|\lesssim _{C,H} n^{-5}+e^{-\Omega (n)}\lesssim n^{-5}$
.
$|\varphi _X(\tau )|\lesssim _{C,H} n^{-5}+e^{-\Omega (n)}\lesssim n^{-5}$
.
Recalling that
![]() $\sigma (X)=\Theta _{C,H}(n^{3/2})$
(and therefore
$\sigma (X)=\Theta _{C,H}(n^{3/2})$
(and therefore
![]() $n^{-1+\gamma /9}\le \alpha n^{1/2+\gamma /8}/\sigma (X)$
for sufficiently large n), we can conclude that for
$n^{-1+\gamma /9}\le \alpha n^{1/2+\gamma /8}/\sigma (X)$
for sufficiently large n), we can conclude that for
![]() $n^{2\gamma }/\sigma (X)\le |\tau |\le \nu $
we have
$n^{2\gamma }/\sigma (X)\le |\tau |\le \nu $
we have
![]() $|\varphi _X(\tau )|\lesssim _{C,H} n^{-5}$
and
$|\varphi _X(\tau )|\lesssim _{C,H} n^{-5}$
and
![]() $|\varphi _X(\tau )-\varphi _Z(\tau )|\lesssim _{C,H} n^{-5}+\exp (-n^{4\gamma }/2)\lesssim n^{-5}$
. Hence, defining
$|\varphi _X(\tau )-\varphi _Z(\tau )|\lesssim _{C,H} n^{-5}+\exp (-n^{4\gamma }/2)\lesssim n^{-5}$
. Hence, defining
![]() $\varepsilon =2/\nu>0$
(which only depends on C), we obtain
$\varepsilon =2/\nu>0$
(which only depends on C), we obtain
 $$\begin{align*}\int_{-2/\varepsilon}^{2/\varepsilon}|\varphi_X(\tau)-\varphi_Z(\tau)|\,d\tau\lesssim_{C,H} \int_{-n^{2\gamma}/\sigma(X)}^{n^{2\gamma}/\sigma(X)}|\tau|n\,d\tau+2\nu\cdot n^{-5}\lesssim_{C,H}n^{4\gamma-2}. \end{align*}$$
$$\begin{align*}\int_{-2/\varepsilon}^{2/\varepsilon}|\varphi_X(\tau)-\varphi_Z(\tau)|\,d\tau\lesssim_{C,H} \int_{-n^{2\gamma}/\sigma(X)}^{n^{2\gamma}/\sigma(X)}|\tau|n\,d\tau+2\nu\cdot n^{-5}\lesssim_{C,H}n^{4\gamma-2}. \end{align*}$$
Let
![]() $B=B(C)=10^4\cdot 2\varepsilon $
. For the upper bound in Theorem 3.1, note that by Lemma 6.1 for all
$B=B(C)=10^4\cdot 2\varepsilon $
. For the upper bound in Theorem 3.1, note that by Lemma 6.1 for all
![]() $x\in \mathbb {R}$
we have (using that
$x\in \mathbb {R}$
we have (using that
![]() $\mathcal {L}(Z,\varepsilon )\le 2\varepsilon /\sigma (X)\lesssim _{C,H} n^{-3/2}$
as
$\mathcal {L}(Z,\varepsilon )\le 2\varepsilon /\sigma (X)\lesssim _{C,H} n^{-3/2}$
as
![]() $p_Z(u)\le 1/\sigma (X)$
for all
$p_Z(u)\le 1/\sigma (X)$
for all
![]() $u\in \mathbb {R}$
)
$u\in \mathbb {R}$
)
 $$\begin{align*}\Pr[|X-x|\leq B]\le 2\cdot 10^4\cdot \mathcal{L}(X,\varepsilon)\lesssim \mathcal{L}(Z,\varepsilon)+\varepsilon \int_{-2/\varepsilon}^{2/\varepsilon}|\varphi_X(\tau)-\varphi_Z(\tau)|\,d\tau\lesssim_{C,H} n^{-3/2}.\end{align*}$$
$$\begin{align*}\Pr[|X-x|\leq B]\le 2\cdot 10^4\cdot \mathcal{L}(X,\varepsilon)\lesssim \mathcal{L}(Z,\varepsilon)+\varepsilon \int_{-2/\varepsilon}^{2/\varepsilon}|\varphi_X(\tau)-\varphi_Z(\tau)|\,d\tau\lesssim_{C,H} n^{-3/2}.\end{align*}$$
For the lower bound in Theorem 3.1, fix some
![]() $A>0$
. We can apply Lemma 6.3 with
$A>0$
. We can apply Lemma 6.3 with
![]() $K=2$
and any fixed
$K=2$
and any fixed
![]() $R\geq 4$
(which we will chose sufficiently large in terms of
$R\geq 4$
(which we will chose sufficiently large in terms of
![]() $C, H, \gamma $
and A). Indeed, note that for any fixed
$C, H, \gamma $
and A). Indeed, note that for any fixed
![]() $A>0$
and
$A>0$
and
![]() $R\geq 4$
, for
$R\geq 4$
, for
![]() $x\in \mathbb Z$
with
$x\in \mathbb Z$
with
![]() $|x-\mathbb {E}X|\leq An^{3/2}$
and
$|x-\mathbb {E}X|\leq An^{3/2}$
and
![]() $y_1,y_2\in [x-R\varepsilon ,x+R\varepsilon ]$
, we have that
$y_1,y_2\in [x-R\varepsilon ,x+R\varepsilon ]$
, we have that
![]() $p_Z(y_1)/p_Z(y_2)\le \exp (-((y_1-\mathbb {E}X)^2-(y_2-\mathbb {E}X)^2)/(2\sigma (X)^2))\le \exp (2R\varepsilon \cdot 4An^{3/2}/\Theta _{C,H}(n^3))\le 2$
if n is sufficiently large with respect to
$p_Z(y_1)/p_Z(y_2)\le \exp (-((y_1-\mathbb {E}X)^2-(y_2-\mathbb {E}X)^2)/(2\sigma (X)^2))\le \exp (2R\varepsilon \cdot 4An^{3/2}/\Theta _{C,H}(n^3))\le 2$
if n is sufficiently large with respect to
![]() $C, H, A$
and R. Hence, Lemma 6.3 yields
$C, H, A$
and R. Hence, Lemma 6.3 yields
 $$ \begin{align*} \Pr[|X-x|\leq B]&\geq \frac{1}{8}\Pr[|Z-x|\le \varepsilon]-C_{6.3}\bigg(R^{-1}\mathcal{L}(Z,\varepsilon)+\varepsilon\int_{-2/\varepsilon}^{2/\varepsilon}|\varphi_Y(\tau)-\varphi_Z(\tau)|\,d\tau\bigg)\\ &\ge \varepsilon\cdot \frac{\exp(-A^2n^3/(2\sigma(X)^2))}{8\sqrt{2\pi}\sigma(X)}-\frac{C_{6.3}}{R}\cdot \frac{2\varepsilon}{\sigma(X)}-C_{6.3}\cdot O_{C,H}(n^{4\gamma-2})\\ &\gtrsim_{C,H,A} n^{-3/2}, \end{align*} $$
$$ \begin{align*} \Pr[|X-x|\leq B]&\geq \frac{1}{8}\Pr[|Z-x|\le \varepsilon]-C_{6.3}\bigg(R^{-1}\mathcal{L}(Z,\varepsilon)+\varepsilon\int_{-2/\varepsilon}^{2/\varepsilon}|\varphi_Y(\tau)-\varphi_Z(\tau)|\,d\tau\bigg)\\ &\ge \varepsilon\cdot \frac{\exp(-A^2n^3/(2\sigma(X)^2))}{8\sqrt{2\pi}\sigma(X)}-\frac{C_{6.3}}{R}\cdot \frac{2\varepsilon}{\sigma(X)}-C_{6.3}\cdot O_{C,H}(n^{4\gamma-2})\\ &\gtrsim_{C,H,A} n^{-3/2}, \end{align*} $$
if R is chosen to be large enough with respect to
![]() $C, H$
and A (recall again that
$C, H$
and A (recall again that
![]() $\sigma (X)=\Theta _{C,H}(n^{3/2})$
).
$\sigma (X)=\Theta _{C,H}(n^{3/2})$
).
10 Robust rank of Ramsey graphs
In [Reference Kwan and Sauermann65], the first and third authors observed that the adjacency matrix of a Ramsey graph is far from any matrix with rank
![]() $O(1)$
. We will need a much stronger version of this fact: The adjacency matrix of a Ramsey graph is far from all matrices built out of a small number of rank-
$O(1)$
. We will need a much stronger version of this fact: The adjacency matrix of a Ramsey graph is far from all matrices built out of a small number of rank-
![]() $O(1)$
‘blocks’ (in the proof of Theorem 3.1, these blocks will correspond to the buckets of vertices with similar values of
$O(1)$
‘blocks’ (in the proof of Theorem 3.1, these blocks will correspond to the buckets of vertices with similar values of
![]() $d_v$
). Recall that
$d_v$
). Recall that
![]() $\lVert M\rVert _{\mathrm {F}}^2$
is the sum of the squares of the entries of M.
$\lVert M\rVert _{\mathrm {F}}^2$
is the sum of the squares of the entries of M.
Lemma 10.1. Fix
![]() $0<\delta <1$
,
$0<\delta <1$
,
![]() $C>0$
,
$C>0$
,
![]() $r\in \mathbb {N}$
and consider a C-Ramsey graph G on n vertices with adjacency matrix A. Suppose we are given a partition
$r\in \mathbb {N}$
and consider a C-Ramsey graph G on n vertices with adjacency matrix A. Suppose we are given a partition
![]() $V(G) = I_1\cup \cdots \cup I_{m}$
, with
$V(G) = I_1\cup \cdots \cup I_{m}$
, with
![]() $|I_1|=\cdots =|I_m|$
and
$|I_1|=\cdots =|I_m|$
and
![]() $n^\delta /2\le m\le 2n^\delta $
. Then, for any
$n^\delta /2\le m\le 2n^\delta $
. Then, for any
![]() $B\in \mathbb {R}^{n\times n}$
with
$B\in \mathbb {R}^{n\times n}$
with
![]() $\operatorname {rank}(B[I_j\!\times \! I_k])\le r$
for all
$\operatorname {rank}(B[I_j\!\times \! I_k])\le r$
for all
![]() $j,k\in [m]$
, we have
$j,k\in [m]$
, we have
![]() $\lVert A-B\rVert _{\mathrm {F}}^2\gtrsim _{C,r,\delta } n^2$
.
$\lVert A-B\rVert _{\mathrm {F}}^2\gtrsim _{C,r,\delta } n^2$
.
The proof of Lemma 10.1 has several ingredients, including the fact that if a binary matrix is close to a low-rank matrix, then it is actually close to a binary low-rank matrix. Note that for binary matrices
![]() $A,Q$
, the squared Frobenius norm
$A,Q$
, the squared Frobenius norm
![]() $\lVert A-Q\rVert _{\operatorname {F}}^2$
can be interpreted as the edit distance between A and B: The minimum number of entries that must be changed to obtain B from A.
$\lVert A-Q\rVert _{\operatorname {F}}^2$
can be interpreted as the edit distance between A and B: The minimum number of entries that must be changed to obtain B from A.
Proposition 10.2. Fix
![]() $r\in \mathbb {N}$
. Consider a binary matrix
$r\in \mathbb {N}$
. Consider a binary matrix
![]() $A\in \{0,1\}^{n\times n}$
and a real matrix
$A\in \{0,1\}^{n\times n}$
and a real matrix
![]() $B\in \mathbb {R}^{n\times n}$
such that
$B\in \mathbb {R}^{n\times n}$
such that
![]() $\operatorname {rank} B\leq r$
and
$\operatorname {rank} B\leq r$
and
![]() $\lVert A-B\rVert _{\operatorname {F}}^2\leq \varepsilon n^2$
for some
$\lVert A-B\rVert _{\operatorname {F}}^2\leq \varepsilon n^2$
for some
![]() $\varepsilon>0$
. Then there is a binary matrix
$\varepsilon>0$
. Then there is a binary matrix
![]() $Q\in \{0,1\}^{n\times n}$
with
$Q\in \{0,1\}^{n\times n}$
with
![]() $\operatorname {rank} Q\leq r$
and
$\operatorname {rank} Q\leq r$
and
![]() $\lVert A-Q\rVert _{\operatorname {F}}^2\le C_r \sqrt \varepsilon n^2$
, for some
$\lVert A-Q\rVert _{\operatorname {F}}^2\le C_r \sqrt \varepsilon n^2$
, for some
![]() $C_r$
depending only on r.
$C_r$
depending only on r.
We remark that it is possible to give a more direct proof of a version of Proposition 10.2 with dramatically worse quantitative aspects (i.e., replacing
![]() $\sqrt \varepsilon $
by a function that decays extremely slowly as
$\sqrt \varepsilon $
by a function that decays extremely slowly as
![]() $\varepsilon \to 0$
), using a bipartite version of the induced graph removal lemma (see, for example, [Reference Conlon and Fox25, Theorem 3.2]). For the application in this paper, quantitative aspects are not important, but we still believe our elementary proof and the strong bounds in Proposition 10.2 are of independent interest (induced removal lemmas typically require the so-called strong regularity lemma, which is notorious for its terrible quantitative aspects). Our proof of Proposition 10.2 relies on the following lemma.
$\varepsilon \to 0$
), using a bipartite version of the induced graph removal lemma (see, for example, [Reference Conlon and Fox25, Theorem 3.2]). For the application in this paper, quantitative aspects are not important, but we still believe our elementary proof and the strong bounds in Proposition 10.2 are of independent interest (induced removal lemmas typically require the so-called strong regularity lemma, which is notorious for its terrible quantitative aspects). Our proof of Proposition 10.2 relies on the following lemma.
Lemma 10.3. Fix
![]() $r\in \mathbb {N}$
. Let
$r\in \mathbb {N}$
. Let
![]() $\eta>0$
, and let
$\eta>0$
, and let
![]() $A\in \{0,1\}^{n\times n}$
be a binary matrix where every entry is colored either red or green, in such a way that fewer than
$A\in \{0,1\}^{n\times n}$
be a binary matrix where every entry is colored either red or green, in such a way that fewer than
![]() $\eta ^2/(10\cdot 2^r)^2\cdot n^2$
entries are red. Suppose that every
$\eta ^2/(10\cdot 2^r)^2\cdot n^2$
entries are red. Suppose that every
![]() $(r+1)\times (r+1)$
submatrix of A consisting only of green entries is singular. Then there exists a binary matrix
$(r+1)\times (r+1)$
submatrix of A consisting only of green entries is singular. Then there exists a binary matrix
![]() $Q\in \{0,1\}^{n\times n}$
with
$Q\in \{0,1\}^{n\times n}$
with
![]() $\operatorname {rank} Q\leq r$
which differs from A in at most
$\operatorname {rank} Q\leq r$
which differs from A in at most
![]() $\eta \cdot n^2$
entries.
$\eta \cdot n^2$
entries.
Proof. For
![]() $\ell \in \mathbb N$
, let us call an
$\ell \in \mathbb N$
, let us call an
![]() $\ell \times \ell $
submatrix of some matrix green if all its
$\ell \times \ell $
submatrix of some matrix green if all its
![]() $\ell ^2$
entries are green.
$\ell ^2$
entries are green.
First, consider all rows and columns of A that contain at least
![]() $\eta /(10\cdot 2^{2r})\cdot n$
red entries. There can be at most
$\eta /(10\cdot 2^{2r})\cdot n$
red entries. There can be at most
![]() $(\eta /10)\cdot n$
such rows and at most
$(\eta /10)\cdot n$
such rows and at most
![]() $(\eta /10)\cdot n$
such columns. Let us define a new matrix
$(\eta /10)\cdot n$
such columns. Let us define a new matrix
![]() $A_1\in \{0,1\}^{n\times n}$
where we replace each of these rows by an all-zero row and each of these columns by an all-zero column, and where we recolor all elements in these replaced rows and columns green. Note that then
$A_1\in \{0,1\}^{n\times n}$
where we replace each of these rows by an all-zero row and each of these columns by an all-zero column, and where we recolor all elements in these replaced rows and columns green. Note that then
![]() $A_1$
and A differ in at most
$A_1$
and A differ in at most
![]() $(2\eta /10)\cdot n^2$
entries, and
$(2\eta /10)\cdot n^2$
entries, and
![]() $A_1$
still has the property that each green
$A_1$
still has the property that each green
![]() $(r+1)\times (r+1)$
submatrix is singular. Furthermore, each row and column in
$(r+1)\times (r+1)$
submatrix is singular. Furthermore, each row and column in
![]() $A_1$
contains at most
$A_1$
contains at most
![]() $\eta /(10\cdot 2^{2r})\cdot n$
red entries.
$\eta /(10\cdot 2^{2r})\cdot n$
red entries.
Now, choose
![]() $\ell $
maximal such that
$\ell $
maximal such that
![]() $A_1$
contains a nonsingular green
$A_1$
contains a nonsingular green
![]() $\ell \times \ell $
submatrix. Clearly,
$\ell \times \ell $
submatrix. Clearly,
![]() $\ell \leq r$
, and without loss of generality we assume that the
$\ell \leq r$
, and without loss of generality we assume that the
![]() $\ell \times \ell $
submatrix
$\ell \times \ell $
submatrix
![]() $A_1[\,[\ell ]\!\times \! [\ell ]\,]$
in the top-left corner of
$A_1[\,[\ell ]\!\times \! [\ell ]\,]$
in the top-left corner of
![]() $A_1$
is nonsingular and green. By the choice of
$A_1$
is nonsingular and green. By the choice of
![]() $\ell $
, every green
$\ell $
, every green
![]() $(\ell +1)\times (\ell +1)$
submatrix in
$(\ell +1)\times (\ell +1)$
submatrix in
![]() $A_1$
is singular.
$A_1$
is singular.
Now, in the first
![]() $\ell $
rows of
$\ell $
rows of
![]() $A_1$
there are at most
$A_1$
there are at most
![]() $\ell \cdot \eta /(10\cdot 2^{2r})\cdot n\leq (\eta /10)n$
red entries. For each of these red entries in the first
$\ell \cdot \eta /(10\cdot 2^{2r})\cdot n\leq (\eta /10)n$
red entries. For each of these red entries in the first
![]() $\ell $
rows of
$\ell $
rows of
![]() $A_1$
, let us replace its entire column by green zeroes (i.e., an all-zero column with all entries colored green). Similarly, in the first
$A_1$
, let us replace its entire column by green zeroes (i.e., an all-zero column with all entries colored green). Similarly, in the first
![]() $\ell $
columns of
$\ell $
columns of
![]() $A_1$
there are at most
$A_1$
there are at most
![]() $(\eta /10)n$
red entries, and for each of these red entries let us replace its entire row by green zeroes. We obtain a new matrix
$(\eta /10)n$
red entries, and for each of these red entries let us replace its entire row by green zeroes. We obtain a new matrix
![]() $A_2\in \{0,1\}^{n\times n}$
differing from
$A_2\in \{0,1\}^{n\times n}$
differing from
![]() $A_1$
in at most
$A_1$
in at most
![]() $(2\eta /10)\cdot n^2$
entries. In this matrix
$(2\eta /10)\cdot n^2$
entries. In this matrix
![]() $A_2$
, it is still true that each green
$A_2$
, it is still true that each green
![]() $(\ell +1)\times (\ell +1)$
submatrix in
$(\ell +1)\times (\ell +1)$
submatrix in
![]() $A_1$
is singular but that
$A_1$
is singular but that
![]() $A_2[\,[\ell ]\!\times \![\ell ]\,]$
is nonsingular. Furthermore,
$A_2[\,[\ell ]\!\times \![\ell ]\,]$
is nonsingular. Furthermore,
![]() $A_2$
has no red entries anywhere in the first
$A_2$
has no red entries anywhere in the first
![]() $\ell $
rows or first
$\ell $
rows or first
![]() $\ell $
columns.
$\ell $
columns.
Next, consider the set of columns of
![]() $A_2\in \{0,1\}^{n\times n}$
with indices in
$A_2\in \{0,1\}^{n\times n}$
with indices in
![]() $\{\ell +1,\ldots ,n\}$
. There is a partition
$\{\ell +1,\ldots ,n\}$
. There is a partition
![]() $\{\ell +1,\ldots ,n\}=I_1\cup \cdots \cup I_{2^r}$
such that for each
$\{\ell +1,\ldots ,n\}=I_1\cup \cdots \cup I_{2^r}$
such that for each
![]() $k=1,\ldots ,2^r$
, the columns of
$k=1,\ldots ,2^r$
, the columns of
![]() $A_2$
with indices in
$A_2$
with indices in
![]() $I_k$
all agree in their first
$I_k$
all agree in their first
![]() $\ell $
rows. For each
$\ell $
rows. For each
![]() $k=1,\ldots ,2^r$
with
$k=1,\ldots ,2^r$
with
![]() $|I_k|\leq \eta /(10\cdot 2^r)\cdot n$
, let us replace all columns with indices in
$|I_k|\leq \eta /(10\cdot 2^r)\cdot n$
, let us replace all columns with indices in
![]() $I_k$
by green all-zero columns. Similarly, there is a partition
$I_k$
by green all-zero columns. Similarly, there is a partition
![]() $\{\ell +1,\ldots ,n\}=J_1\cup \cdots \cup J_{2^r}$
such that the rows with indices in the same set
$\{\ell +1,\ldots ,n\}=J_1\cup \cdots \cup J_{2^r}$
such that the rows with indices in the same set
![]() $J_k$
all agree in their first
$J_k$
all agree in their first
![]() $\ell $
columns. For each
$\ell $
columns. For each
![]() $k=1,\ldots ,2^r$
with
$k=1,\ldots ,2^r$
with
![]() $|J_k|\leq \eta /(10\cdot 2^r)\cdot n$
, replace all rows with indices in
$|J_k|\leq \eta /(10\cdot 2^r)\cdot n$
, replace all rows with indices in
![]() $J_k$
with green all-zero rows. In this way, we obtain a new matrix
$J_k$
with green all-zero rows. In this way, we obtain a new matrix
![]() $A_3\in \{0,1\}^{n\times n}$
differing from
$A_3\in \{0,1\}^{n\times n}$
differing from
![]() $A_2$
in at most
$A_2$
in at most
![]() $(2\eta /10)\cdot n^2$
entries. Still, all green
$(2\eta /10)\cdot n^2$
entries. Still, all green
![]() $(\ell +1)\times (\ell +1)$
submatrices in
$(\ell +1)\times (\ell +1)$
submatrices in
![]() $A_3$
are singular,
$A_3$
are singular,
![]() $A_3[\,[\ell ]\!\times \![\ell ]\,]$
is nonsingular, and all entries in the first
$A_3[\,[\ell ]\!\times \![\ell ]\,]$
is nonsingular, and all entries in the first
![]() $\ell $
rows and in the first
$\ell $
rows and in the first
![]() $\ell $
columns of
$\ell $
columns of
![]() $A_3$
are green.
$A_3$
are green.
Finally, define the matrix
![]() $Q\in \{0,1\}^{n\times n}$
by replacing the red entries in
$Q\in \{0,1\}^{n\times n}$
by replacing the red entries in
![]() $A_3$
as follows. For each red entry
$A_3$
as follows. For each red entry
![]() $(j,i)$
in
$(j,i)$
in
![]() $A_3$
we have
$A_3$
we have
![]() $j\in J_k$
and
$j\in J_k$
and
![]() $i\in I_{k'}$
for some k and
$i\in I_{k'}$
for some k and
![]() $k'$
such that
$k'$
such that
![]() $|J_k|, |I_{k'}|> \eta /(10\cdot 2^r)\cdot n$
. So, the submatrix
$|J_k|, |I_{k'}|> \eta /(10\cdot 2^r)\cdot n$
. So, the submatrix
![]() $A_3[J_k\!\times \! I_{k'}]$
of
$A_3[J_k\!\times \! I_{k'}]$
of
![]() $A_3$
must contain at least one green entry (since
$A_3$
must contain at least one green entry (since
![]() $A_3$
has fewer than
$A_3$
has fewer than
![]() $\eta ^2/(10\cdot 2^r)^2\cdot n^2$
red entries). Let us now replace the red
$\eta ^2/(10\cdot 2^r)^2\cdot n^2$
red entries). Let us now replace the red
![]() $(j,i)$
-entry in
$(j,i)$
-entry in
![]() $A_3$
by some green entry in
$A_3$
by some green entry in
![]() $A_3[J_k\!\times \! I_{k'}]$
. Replacing all red entries in this way, we obtain a matrix
$A_3[J_k\!\times \! I_{k'}]$
. Replacing all red entries in this way, we obtain a matrix
![]() $Q\in \{0,1\}^{n\times n}$
differing from
$Q\in \{0,1\}^{n\times n}$
differing from
![]() $A_3$
in at most
$A_3$
in at most
![]() $\eta ^2/(10\cdot 2^r)^2\cdot n^2\leq (\eta /10)\cdot n^2$
entries.
$\eta ^2/(10\cdot 2^r)^2\cdot n^2\leq (\eta /10)\cdot n^2$
entries.
All in all, Q differs from A in at most
![]() $(7\eta /10)\cdot n^2\leq \eta \cdot n^2$
entries. The
$(7\eta /10)\cdot n^2\leq \eta \cdot n^2$
entries. The
![]() $\ell \times \ell $
submatrix
$\ell \times \ell $
submatrix
![]() $Q[\,[\ell ]\!\times \![\ell ]\,]$
is still nonsingular. We claim that whenever we extend this
$Q[\,[\ell ]\!\times \![\ell ]\,]$
is still nonsingular. We claim that whenever we extend this
![]() $\ell \times \ell $
submatrix in Q to an
$\ell \times \ell $
submatrix in Q to an
![]() $(\ell +1)\times (\ell +1)$
submatrix by taking an additional row
$(\ell +1)\times (\ell +1)$
submatrix by taking an additional row
![]() $j\in \{\ell +1,\ldots ,n\}$
and an additional column
$j\in \{\ell +1,\ldots ,n\}$
and an additional column
![]() $i\in \{\ell +1,\ldots ,n\}$
, the resulting
$i\in \{\ell +1,\ldots ,n\}$
, the resulting
![]() $(\ell +1)\times (\ell +1)$
submatrix of Q is singular. If the
$(\ell +1)\times (\ell +1)$
submatrix of Q is singular. If the
![]() $(j,i)$
-entry in
$(j,i)$
-entry in
![]() $A_3$
is green, then this
$A_3$
is green, then this
![]() $(\ell +1)\times (\ell +1)$
submatrix of Q agrees with the corresponding submatrix in
$(\ell +1)\times (\ell +1)$
submatrix of Q agrees with the corresponding submatrix in
![]() $A_3$
, which is green and therefore singular. If the
$A_3$
, which is green and therefore singular. If the
![]() $(j,i)$
-entry in
$(j,i)$
-entry in
![]() $A_3$
is red, then the
$A_3$
is red, then the
![]() $(j,i)$
-entry in Q agrees with some green
$(j,i)$
-entry in Q agrees with some green
![]() $(j',i')$
-entry in
$(j',i')$
-entry in
![]() $A_3$
, where
$A_3$
, where
![]() $j,j'\in J_k$
and
$j,j'\in J_k$
and
![]() $i,i'\in I_{k'}$
for some
$i,i'\in I_{k'}$
for some
![]() $k,k'$
. Hence, the desired
$k,k'$
. Hence, the desired
![]() $(\ell +1)\times (\ell +1)$
submatrix of Q agrees with the
$(\ell +1)\times (\ell +1)$
submatrix of Q agrees with the
![]() $(\ell +1)\times (\ell +1)$
submatrix
$(\ell +1)\times (\ell +1)$
submatrix
![]() $A_3[\,([\ell ]\cup \{i'\})\!\times \!([\ell ]\cup \{j'\})\,]$
of
$A_3[\,([\ell ]\cup \{i'\})\!\times \!([\ell ]\cup \{j'\})\,]$
of
![]() $A_3$
, which is green and therefore singular. Hence, we have shown that all
$A_3$
, which is green and therefore singular. Hence, we have shown that all
![]() $(\ell +1)\times (\ell +1)$
submatrices of Q that contain
$(\ell +1)\times (\ell +1)$
submatrices of Q that contain
![]() $Q[\,[\ell ]\!\times \![\ell ]\,]$
are singular. Since
$Q[\,[\ell ]\!\times \![\ell ]\,]$
are singular. Since
![]() $Q[\,[\ell ]\!\times \![\ell ]\,]$
is nonsingular, this implies that
$Q[\,[\ell ]\!\times \![\ell ]\,]$
is nonsingular, this implies that
![]() $\operatorname {rank} Q = \ell \leq r$
.
$\operatorname {rank} Q = \ell \leq r$
.
Now, we are ready to prove Proposition 10.2.
Proof of Proposition 10.2
Choose some
![]() $0<c_r<1$
depending only on r such thatFootnote 9
$0<c_r<1$
depending only on r such thatFootnote 9
where
![]() $\lVert S-T\rVert _{\infty }$
denotes the maximum absolute value
$\lVert S-T\rVert _{\infty }$
denotes the maximum absolute value
![]() $|(S-T)_{i,j}|$
among the entries of
$|(S-T)_{i,j}|$
among the entries of
![]() $S-T$
.
$S-T$
.
Let A and B be matrices as in the lemma statement. Let us color each entry
![]() $A_{i,j}$
of A red if
$A_{i,j}$
of A red if
![]() $|A_{i,j}-B_{i,j}|^2> c_r$
and green otherwise. Then, as
$|A_{i,j}-B_{i,j}|^2> c_r$
and green otherwise. Then, as
![]() $\lVert A-B\rVert _{\operatorname {F}}^2\leq \varepsilon n^2$
, there are fewer than
$\lVert A-B\rVert _{\operatorname {F}}^2\leq \varepsilon n^2$
, there are fewer than
![]() $\varepsilon n^2/c_r$
red entries in A. Furthermore, as
$\varepsilon n^2/c_r$
red entries in A. Furthermore, as
![]() $\operatorname {rank} B\leq r$
, by the choice of
$\operatorname {rank} B\leq r$
, by the choice of
![]() $c_r$
, every
$c_r$
, every
![]() $(r+1)\times (r+1)$
submatrix of A consisting only of green entries must be singular. Thus, taking
$(r+1)\times (r+1)$
submatrix of A consisting only of green entries must be singular. Thus, taking
![]() $C_r=10\cdot 2^r/\sqrt {c_r}$
the desired statement follows from Lemma 10.3 with
$C_r=10\cdot 2^r/\sqrt {c_r}$
the desired statement follows from Lemma 10.3 with
![]() $\eta =(10\cdot 2^r)\sqrt {\varepsilon /c_r}$
.
$\eta =(10\cdot 2^r)\sqrt {\varepsilon /c_r}$
.
We also need the simple fact that low-rank binary matrices can be partitioned into a small number of homogeneous parts. This essentially corresponds to a classical bound on the log-rank conjecture.
Lemma 10.4. Fix
![]() $r\in \mathbb {N}$
, and let
$r\in \mathbb {N}$
, and let
![]() $s=2^r$
. For any binary matrix
$s=2^r$
. For any binary matrix
![]() $Q\in \{0,1\}^{n\times n}$
with
$Q\in \{0,1\}^{n\times n}$
with
![]() $\operatorname {rank} Q\leq r$
, we can find partitions
$\operatorname {rank} Q\leq r$
, we can find partitions
![]() $P_1\cup \cdots \cup P_{s}$
and
$P_1\cup \cdots \cup P_{s}$
and
![]() $R_1\cup \cdots \cup R_{s}$
of
$R_1\cup \cdots \cup R_{s}$
of
![]() $[n]$
such that for all
$[n]$
such that for all
![]() $i,j\in [s]$
, the submatrix
$i,j\in [s]$
, the submatrix
![]() $Q[P_i\!\times \! R_j]$
consists of only zeroes or only ones.
$Q[P_i\!\times \! R_j]$
consists of only zeroes or only ones.
Proof. First, we claim that the matrix Q has most
![]() $2^r$
different row vectors: Indeed, let
$2^r$
different row vectors: Indeed, let
![]() $r'=\operatorname {rank} Q\leq r$
and suppose without loss of generality that the submatrix
$r'=\operatorname {rank} Q\leq r$
and suppose without loss of generality that the submatrix
![]() $Q[\,[r']\!\times \! [r']\,]$
is nonsingular. Then each row of Q can be expressed as a linear combination of the first
$Q[\,[r']\!\times \! [r']\,]$
is nonsingular. Then each row of Q can be expressed as a linear combination of the first
![]() $r'$
rows, and any two rows of Q which agree in the first
$r'$
rows, and any two rows of Q which agree in the first
![]() $r'$
entries must be given by the same linear combination. Hence, there can be at most
$r'$
entries must be given by the same linear combination. Hence, there can be at most
![]() $2^r=s$
different row vectors in the matrix Q, and we obtain a partition
$2^r=s$
different row vectors in the matrix Q, and we obtain a partition
![]() $[n]=P_1\cup \cdots \cup P_{s}$
such that any two rows with indices in the same set
$[n]=P_1\cup \cdots \cup P_{s}$
such that any two rows with indices in the same set
![]() $P_i$
are identical.
$P_i$
are identical.
Similarly, there is a partition
![]() $[n]=P_1\cup \cdots \cup P_{s}$
such that any two columns with indices in the same set
$[n]=P_1\cup \cdots \cup P_{s}$
such that any two columns with indices in the same set
![]() $R_j$
are identical. Now, for all
$R_j$
are identical. Now, for all
![]() $i,j\in [s]$
, all entries of the submatrix
$i,j\in [s]$
, all entries of the submatrix
![]() $Q[P_i\!\times \! R_j]$
must be identical to each other, that is, must be either all zeroes or all ones.
$Q[P_i\!\times \! R_j]$
must be identical to each other, that is, must be either all zeroes or all ones.
Apart from Proposition 10.2 and Lemma 10.4, in our proof of Lemma 10.1 we will also use the fact that every n-vertex graph has a clique or independent set of size at least
![]() $\frac 12\log n$
(this is a quantitative version of Ramsey’s theorem proved by Erdős and Szekeres [Reference Erdős and Szekeres38], as mentioned in the introduction).
$\frac 12\log n$
(this is a quantitative version of Ramsey’s theorem proved by Erdős and Szekeres [Reference Erdős and Szekeres38], as mentioned in the introduction).
Proof of Lemma 10.1
By Theorem 4.1, there exists some
![]() $\alpha =\alpha (C,\delta )>0$
such that every
$\alpha =\alpha (C,\delta )>0$
such that every
![]() $2C/(1-\delta )$
-Ramsey graph on sufficiently many vertices has density at least
$2C/(1-\delta )$
-Ramsey graph on sufficiently many vertices has density at least
![]() $\alpha $
and at most
$\alpha $
and at most
![]() $1-\alpha $
. Fix a sufficiently large integer
$1-\alpha $
. Fix a sufficiently large integer
![]() $D=D(C,\delta )$
such that
$D=D(C,\delta )$
such that
![]() $1/\log _2 D<\alpha /4$
, and choose
$1/\log _2 D<\alpha /4$
, and choose
![]() $\varepsilon =\varepsilon (C,r,\delta )>0$
small enough such that
$\varepsilon =\varepsilon (C,r,\delta )>0$
small enough such that
![]() $\sqrt {\varepsilon }<1/D^2$
and
$\sqrt {\varepsilon }<1/D^2$
and
![]() $\varepsilon ^{1/4}<\alpha /(2^{2rD+1}C_r)$
, where
$\varepsilon ^{1/4}<\alpha /(2^{2rD+1}C_r)$
, where
![]() $C_r$
is the constant in Proposition 10.2. It suffices to prove that we have
$C_r$
is the constant in Proposition 10.2. It suffices to prove that we have
![]() $\|A-B\|^2_{\mathrm F}\ge \varepsilon n^2$
if n is sufficiently large with respect to
$\|A-B\|^2_{\mathrm F}\ge \varepsilon n^2$
if n is sufficiently large with respect to
![]() $C,\delta $
, and r. So let us assume for contradiction that
$C,\delta $
, and r. So let us assume for contradiction that
![]() $\|A-B\|^2_{\mathrm F}< \varepsilon n^2$
.
$\|A-B\|^2_{\mathrm F}< \varepsilon n^2$
.
Note that
![]() $\sum _{1\le k<j\le m}\big \|(A-B)[I_j\!\times \! I_k]\big \|_{\mathrm F}^2\le \|A-B\|_{\mathrm F}^2\le \varepsilon n^2$
, so there can be at most
$\sum _{1\le k<j\le m}\big \|(A-B)[I_j\!\times \! I_k]\big \|_{\mathrm F}^2\le \|A-B\|_{\mathrm F}^2\le \varepsilon n^2$
, so there can be at most
![]() $\sqrt {\varepsilon }m^2$
pairs
$\sqrt {\varepsilon }m^2$
pairs
![]() $(j,k)$
with
$(j,k)$
with
![]() $1\le j<k\le m$
such that
$1\le j<k\le m$
such that
![]() $\big \|(A-B)[I_j\!\times \! I_k]\big \|_{\mathrm F}^2\ge \sqrt {\varepsilon }(n/m)^2$
. Hence, a uniformly random subset of
$\big \|(A-B)[I_j\!\times \! I_k]\big \|_{\mathrm F}^2\ge \sqrt {\varepsilon }(n/m)^2$
. Hence, a uniformly random subset of
![]() $[m]$
of size D contains such a pair
$[m]$
of size D contains such a pair
![]() $(j,k)$
with probability at most
$(j,k)$
with probability at most
![]() $\binom {D}{2}\cdot \sqrt {\varepsilon }<1$
. Thus, there exists a subset of
$\binom {D}{2}\cdot \sqrt {\varepsilon }<1$
. Thus, there exists a subset of
![]() $[m]$
of size D not containing any such pair
$[m]$
of size D not containing any such pair
![]() $(j,k)$
, and we may assume without loss of generality that
$(j,k)$
, and we may assume without loss of generality that
![]() $[D]$
is such a subset. Then for any
$[D]$
is such a subset. Then for any
![]() $1\le j<k\le D$
we have
$1\le j<k\le D$
we have
![]() $\big \|(A-B)[I_j\!\times \! I_k]\big \|_{\mathrm F}^2< \sqrt {\varepsilon }(n/m)^2=\sqrt {\varepsilon }\cdot |I_j|\cdot |I_k|$
.
$\big \|(A-B)[I_j\!\times \! I_k]\big \|_{\mathrm F}^2< \sqrt {\varepsilon }(n/m)^2=\sqrt {\varepsilon }\cdot |I_j|\cdot |I_k|$
.
For any
![]() $1\le j<k\le D$
, by Proposition 10.2 (recalling that
$1\le j<k\le D$
, by Proposition 10.2 (recalling that
![]() $\operatorname {rank}(B[I_j\!\times \! I_k])\le r$
) we can find a binary matrix
$\operatorname {rank}(B[I_j\!\times \! I_k])\le r$
) we can find a binary matrix
![]() $Q^{(j,k)}\in \{0,1\}^{I_j\!\times \! I_k}$
with
$Q^{(j,k)}\in \{0,1\}^{I_j\!\times \! I_k}$
with
![]() $\operatorname {rank}(Q^{(j,k)})\le r$
and
$\operatorname {rank}(Q^{(j,k)})\le r$
and
![]() $\|A[I_j\!\times \! I_k]-Q^{(j,k)}\|_{\mathrm F}^2\le C_r \varepsilon ^{1/4} (n/m)^2$
. Now, by Lemma 10.4, we can find partitions of
$\|A[I_j\!\times \! I_k]-Q^{(j,k)}\|_{\mathrm F}^2\le C_r \varepsilon ^{1/4} (n/m)^2$
. Now, by Lemma 10.4, we can find partitions of
![]() $I_j$
and
$I_j$
and
![]() $I_k$
into
$I_k$
into
![]() $2^r$
parts each, such that the corresponding
$2^r$
parts each, such that the corresponding
![]() $(2^r)^2$
submatrices of
$(2^r)^2$
submatrices of
![]() $Q^{(j,k)}$
each consist either only of zeroes or only of ones. Let us choose such partitions for all pairs
$Q^{(j,k)}$
each consist either only of zeroes or only of ones. Let us choose such partitions for all pairs
![]() $(j,k)$
with
$(j,k)$
with
![]() $1\le j<k\le D$
, and for each of the sets
$1\le j<k\le D$
, and for each of the sets
![]() $I_1,\ldots ,I_D$
, let us take a common refinement of the
$I_1,\ldots ,I_D$
, let us take a common refinement of the
![]() $D-1$
partitions of that set. This way, for each of the sets
$D-1$
partitions of that set. This way, for each of the sets
![]() $I_1,\ldots ,I_D$
we obtain a partition into
$I_1,\ldots ,I_D$
we obtain a partition into
![]() $2^{r(D-1)}$
parts in such a way that for all
$2^{r(D-1)}$
parts in such a way that for all
![]() $1\le j<k\le D$
each of the submatrices of
$1\le j<k\le D$
each of the submatrices of
![]() $Q^{(j,k)}$
induced by the partitions of
$Q^{(j,k)}$
induced by the partitions of
![]() $I_j$
and
$I_j$
and
![]() $I_k$
consist either only of zeroes or only of ones.
$I_k$
consist either only of zeroes or only of ones.
For each
![]() $j=1,\ldots ,D$
, inside one of the parts of this partition of
$j=1,\ldots ,D$
, inside one of the parts of this partition of
![]() $I_j$
, we can now choose a subset
$I_j$
, we can now choose a subset
![]() $I_j'\subseteq I_j$
of size
$I_j'\subseteq I_j$
of size
![]() $|I_j'|=\lceil |I_j|/2^{r(D-1)}\rceil =\lceil n/(2^{r(D-1)}m)\rceil $
. Then for all
$|I_j'|=\lceil |I_j|/2^{r(D-1)}\rceil =\lceil n/(2^{r(D-1)}m)\rceil $
. Then for all
![]() $1\le j<k\le D$
, the submatrix
$1\le j<k\le D$
, the submatrix
![]() $Q^{(j,k)}[I_j',I_k']$
consists either only of zeroes or only of ones. Consider the graph H on the vertex set
$Q^{(j,k)}[I_j',I_k']$
consists either only of zeroes or only of ones. Consider the graph H on the vertex set
![]() $[D]$
where for
$[D]$
where for
![]() $1\le j<k\le D$
we draw an edge if all entries of
$1\le j<k\le D$
we draw an edge if all entries of
![]() $Q^{(j,k)}[I_j',I_k']$
are one (and we don’t draw an edge if all entries are zero). Then, by Ramsey’s theorem (specifically, Erdős and Szekeres’ classical bound [Reference Erdős and Szekeres38]), this graph H must have a clique or independent set
$Q^{(j,k)}[I_j',I_k']$
are one (and we don’t draw an edge if all entries are zero). Then, by Ramsey’s theorem (specifically, Erdős and Szekeres’ classical bound [Reference Erdős and Szekeres38]), this graph H must have a clique or independent set
![]() $S\subseteq [D]$
of size
$S\subseteq [D]$
of size
![]() $|S|\geq (\log _2 D)/2$
. Without loss of generality, assume that
$|S|\geq (\log _2 D)/2$
. Without loss of generality, assume that
![]() $S=\{1,\ldots ,|S|\}$
. Let us now consider the induced subgraph of the original graph G on the vertex set
$S=\{1,\ldots ,|S|\}$
. Let us now consider the induced subgraph of the original graph G on the vertex set
![]() $I_1'\cup \cdots \cup I_{|S|}'$
.
$I_1'\cup \cdots \cup I_{|S|}'$
.
If
![]() $S=\{1,\ldots ,|S|\}$
is an independent set in H, then for all
$S=\{1,\ldots ,|S|\}$
is an independent set in H, then for all
![]() $1\leq j<k\leq |S|$
the matrix
$1\leq j<k\leq |S|$
the matrix
![]() $Q^{(j,k)}[I_j'\!\times \!I_k']$
is all-zero, so
$Q^{(j,k)}[I_j'\!\times \!I_k']$
is all-zero, so
![]() $A[I_j\!\times \! I_k]\in \{0,1\}^{I_j\!\times \! I_k}$
can contain at most
$A[I_j\!\times \! I_k]\in \{0,1\}^{I_j\!\times \! I_k}$
can contain at most
![]() $C_r \varepsilon ^{1/4} (n/m)^2$
ones (since
$C_r \varepsilon ^{1/4} (n/m)^2$
ones (since
![]() $\|A[I_j\!\times \! I_k]-Q^{(j,k)}\|_{\mathrm F}^2\le C_r \varepsilon ^{1/4} (n/m)^2$
). In other words, for all
$\|A[I_j\!\times \! I_k]-Q^{(j,k)}\|_{\mathrm F}^2\le C_r \varepsilon ^{1/4} (n/m)^2$
). In other words, for all
![]() $1\leq j<k\leq |S|$
the graph
$1\leq j<k\leq |S|$
the graph
![]() $G[I_1'\cup \cdots \cup I_{|S|}']$
has at most
$G[I_1'\cup \cdots \cup I_{|S|}']$
has at most
![]() $C_r \varepsilon ^{1/4} (n/m)^2\leq C_r \varepsilon ^{1/4}\cdot 2^{2r(D-1)}\cdot |I_j'|\cdot |I_k'|\leq (\alpha /2)\cdot |I_j'|\cdot |I_{k}'|$
edges between
$C_r \varepsilon ^{1/4} (n/m)^2\leq C_r \varepsilon ^{1/4}\cdot 2^{2r(D-1)}\cdot |I_j'|\cdot |I_k'|\leq (\alpha /2)\cdot |I_j'|\cdot |I_{k}'|$
edges between
![]() $I_j'$
and
$I_j'$
and
![]() $I_k'$
. As
$I_k'$
. As
![]() $|I_1'|=\cdots =|I_{|S|}'|$
, the edges within the sets
$|I_1'|=\cdots =|I_{|S|}'|$
, the edges within the sets
![]() $I_1,\ldots ,I_k$
also contribute at most
$I_1,\ldots ,I_k$
also contribute at most
![]() $1/|S|\leq 2/\log _2 D<\alpha /2$
to the density of
$1/|S|\leq 2/\log _2 D<\alpha /2$
to the density of
![]() $G[I_1'\cup \cdots \cup I_{|S|}']$
. Thus, the graph
$G[I_1'\cup \cdots \cup I_{|S|}']$
. Thus, the graph
![]() $G[I_1'\cup \cdots \cup I_{|S|}']$
has density less than
$G[I_1'\cup \cdots \cup I_{|S|}']$
has density less than
![]() $\alpha $
, but it is a
$\alpha $
, but it is a
![]() $2C/(1-\delta )$
-Ramsey graph since
$2C/(1-\delta )$
-Ramsey graph since
![]() $|I_1'\cup \cdots \cup I_{|S|}'|\geq n/(2^{r(D-1)}m)\geq n^{1-\delta }/2^{r(D-1)+1}\geq n^{(1-\delta )/2}$
. This is a contradiction.
$|I_1'\cup \cdots \cup I_{|S|}'|\geq n/(2^{r(D-1)}m)\geq n^{1-\delta }/2^{r(D-1)+1}\geq n^{(1-\delta )/2}$
. This is a contradiction.
Similarly, if
![]() $S=\{1,\ldots ,|S|\}$
is a clique in H, then for all
$S=\{1,\ldots ,|S|\}$
is a clique in H, then for all
![]() $1\leq j<k\leq |S|$
the matrix
$1\leq j<k\leq |S|$
the matrix
![]() $Q^{(j,k)}[I_j',I_k']$
is an all-ones matrix, and we can perform a similar calculation for the number of nonedges in
$Q^{(j,k)}[I_j',I_k']$
is an all-ones matrix, and we can perform a similar calculation for the number of nonedges in
![]() $G[I_1'\cup \cdots \cup I_{|S|}']$
. We find that
$G[I_1'\cup \cdots \cup I_{|S|}']$
. We find that
![]() $G[I_1'\cup \cdots \cup I_{|S|}']$
has density greater than
$G[I_1'\cup \cdots \cup I_{|S|}']$
has density greater than
![]() $1-\alpha $
, which is again a contradiction.
$1-\alpha $
, which is again a contradiction.
11 Lemmas for products of Boolean slices
In this section we study products of Boolean slices (that is, we consider random vectors
![]() $\vec x\in \{-1,1\}^n$
whose index set is divided into ‘buckets’, uniform among all vectors with a particular number of ‘1’s in each bucket). The main outputs we will need from this section are summarized in the following lemma. Namely, for a ‘well behaved’ quadratic polynomial f, a Gaussian vector
$\vec x\in \{-1,1\}^n$
whose index set is divided into ‘buckets’, uniform among all vectors with a particular number of ‘1’s in each bucket). The main outputs we will need from this section are summarized in the following lemma. Namely, for a ‘well behaved’ quadratic polynomial f, a Gaussian vector
![]() $\vec z$
and a vector
$\vec z$
and a vector
![]() $\vec x$
sampled from an appropriate product of slices, we can compare
$\vec x$
sampled from an appropriate product of slices, we can compare
![]() $f(\vec x)$
with
$f(\vec x)$
with
![]() $f(\vec z)$
. Our assumptions on f are certain bounds on the coefficients, and that our polynomial is in a certain sense ‘balanced’ within each bucket.
$f(\vec z)$
. Our assumptions on f are certain bounds on the coefficients, and that our polynomial is in a certain sense ‘balanced’ within each bucket.
Lemma 11.1. Fix
![]() $0<\delta <1/4$
. Suppose we are given a partition
$0<\delta <1/4$
. Suppose we are given a partition
![]() $[n] = I_1\cup \cdots \cup I_{m}$
, with
$[n] = I_1\cup \cdots \cup I_{m}$
, with
![]() $|I_1|=\cdots =|I_m|$
and
$|I_1|=\cdots =|I_m|$
and
![]() $n^\delta /2\le m\le 2n^\delta $
, where n is sufficiently large with respect to
$n^\delta /2\le m\le 2n^\delta $
, where n is sufficiently large with respect to
![]() $\delta $
. Consider a symmetric matrix
$\delta $
. Consider a symmetric matrix
![]() $F\in \mathbb {R}^{n\times n}$
, a vector
$F\in \mathbb {R}^{n\times n}$
, a vector
![]() $\vec f\in \mathbb {R}^{n}$
and a real number
$\vec f\in \mathbb {R}^{n}$
and a real number
![]() $f_0$
satisfying the following conditions:
$f_0$
satisfying the following conditions:
-
(a)
 $\lVert \vec {f}\rVert _{\infty }\le n^{1/2+3\delta }$
.
$\lVert \vec {f}\rVert _{\infty }\le n^{1/2+3\delta }$
. -
(b)
 $|F_{i,j}|\le 1$
for all
$|F_{i,j}|\le 1$
for all
 $i,j\in [n]$
.
$i,j\in [n]$
. -
(c) For each
 $k=1,\ldots ,m$
, the sum of the entries in
$k=1,\ldots ,m$
, the sum of the entries in
 $\vec f_{I_k}$
is equal to zero.
$\vec f_{I_k}$
is equal to zero. -
(d) For all
 $k,h\in [m]$
, in the submatrix
$k,h\in [m]$
, in the submatrix
 $F[I_k\!\times \! I_h]$
of F all row and column sums are zero.
$F[I_k\!\times \! I_h]$
of F all row and column sums are zero.
Consider a sequence
![]() $(\ell _1,\ldots ,\ell _m)\in \mathbb {N}^{m}$
with
$(\ell _1,\ldots ,\ell _m)\in \mathbb {N}^{m}$
with
![]() $|\ell _{k}-|I_k|/2|\le \sqrt {n^{1-\delta }}\log n$
for
$|\ell _{k}-|I_k|/2|\le \sqrt {n^{1-\delta }}\log n$
for
![]() $k=1,\ldots ,m$
. Then, let
$k=1,\ldots ,m$
. Then, let
![]() $\vec {x}\in \{-1,1\}^{n}$
be a uniformly random vector such that
$\vec {x}\in \{-1,1\}^{n}$
be a uniformly random vector such that
![]() $\vec {x}_{I_{k}}$
has exactly
$\vec {x}_{I_{k}}$
has exactly
![]() $\ell _{k}$
ones for each
$\ell _{k}$
ones for each
![]() $k=1,\ldots ,m$
, and let
$k=1,\ldots ,m$
, and let
![]() $\vec z\sim \mathcal {N}(0,1)^{\otimes n}$
be a vector of independent standard Gaussian random variables. Define
$\vec z\sim \mathcal {N}(0,1)^{\otimes n}$
be a vector of independent standard Gaussian random variables. Define
![]() $X=f_0+\vec f\cdot \vec {x}+\vec {x}^{\intercal }F\vec {x}$
and
$X=f_0+\vec f\cdot \vec {x}+\vec {x}^{\intercal }F\vec {x}$
and
![]() $Z=f_0+\vec f\cdot \vec {z}+\vec {z}^{\intercal }F\vec {z}$
. Then the following three statements hold.
$Z=f_0+\vec f\cdot \vec {z}+\vec {z}^{\intercal }F\vec {z}$
. Then the following three statements hold.
-
1.
 $\mathbb {E} X=f_0+\sum _{i=1}^{n}F_{i,i}+O(n^{3/4+4\delta })$
and
$\mathbb {E} X=f_0+\sum _{i=1}^{n}F_{i,i}+O(n^{3/4+4\delta })$
and
 $\mathbb {E} Z=f_0+\sum _{i=1}^{n}F_{i,i}$
.
$\mathbb {E} Z=f_0+\sum _{i=1}^{n}F_{i,i}$
. -
2.
 $\sigma (X)^2=2\|F\|_{\mathrm F}^2+\|\vec f\|_2^2+O(n^{7/4+7\delta })$
and
$\sigma (X)^2=2\|F\|_{\mathrm F}^2+\|\vec f\|_2^2+O(n^{7/4+7\delta })$
and
 $\sigma (Z)^2=2\|F\|_{\mathrm F}^2+\|\vec f\|_2^2$
.
$\sigma (Z)^2=2\|F\|_{\mathrm F}^2+\|\vec f\|_2^2$
. -
3. For any
 $\tau \in \mathbb {R}$
, we have
$\tau \in \mathbb {R}$
, we have  $$\begin{align*}|\varphi_X(\tau)-\varphi_Z(\tau)|\lesssim |\tau|^4\cdot n^{3+12\delta}+|\tau|\cdot n^{3/4+4\delta}.\end{align*}$$
$$\begin{align*}|\varphi_X(\tau)-\varphi_Z(\tau)|\lesssim |\tau|^4\cdot n^{3+12\delta}+|\tau|\cdot n^{3/4+4\delta}.\end{align*}$$
We will apply this lemma in the additively structured case of our proof of Theorem 3.1. In that proof, we will use Lemma 4.12 to partition (most of) the vertices of our graph into ‘buckets’, where vertices in the same bucket have similar values of
![]() $d_v$
(for the vector
$d_v$
(for the vector
![]() $\vec {d}$
defined in Definition 9.1). This choice of buckets will ensure that (a) holds, for a conditional random variable obtained by conditioning on the number of vertices in each bucket (the resulting conditional distribution is a product of slices).
$\vec {d}$
defined in Definition 9.1). This choice of buckets will ensure that (a) holds, for a conditional random variable obtained by conditioning on the number of vertices in each bucket (the resulting conditional distribution is a product of slices).
We also remark that the precise form of the right-hand side of the inequality in (3) is not important; we only need that
![]() $\int _{|\tau |\le n^{-0.99}}|\varphi _X(\tau )-\varphi _Z(\tau )|\,d\tau $
is substantially smaller than
$\int _{|\tau |\le n^{-0.99}}|\varphi _X(\tau )-\varphi _Z(\tau )|\,d\tau $
is substantially smaller than
![]() $1/\sigma (X)$
(for small
$1/\sigma (X)$
(for small
![]() $\delta $
).
$\delta $
).
Lemma 11.1 can be interpreted as a type of Gaussian invariance principle, comparing quadratic functions of products of slices to Gaussian analogs. There are already some invariance principles available for the Boolean slice (see [Reference Filmus and Mossel43, Reference Filmus, Kindler, Mossel and Wimmer42]), and it would likely be possible to prove Lemma 11.1 by repeatedly applying results from [Reference Filmus and Mossel43, Reference Filmus, Kindler, Mossel and Wimmer42] to the individual factors of our product of slices. However, for our specific application it will be more convenient to deduce Lemma 11.1 from a Gaussian invariance principle for products of Rademacher random variables.
Indeed, we will first compare X to its ‘independent Rademacher analog’ (i.e., to the random variable Y defined as
![]() $Y=f_0+\vec f\cdot \vec {y}+\vec {y}^{\intercal }F\vec {y}$
, where
$Y=f_0+\vec f\cdot \vec {y}+\vec {y}^{\intercal }F\vec {y}$
, where
![]() $\vec {y}\in \{-1,1\}^n$
is uniformly random). In order to do this, we will first show that for different choices of the sequence
$\vec {y}\in \{-1,1\}^n$
is uniformly random). In order to do this, we will first show that for different choices of the sequence
![]() $(\ell _1,\ldots ,\ell _m)$
, we can closely couple the resulting random variables X (essentially, we just randomly ‘flip the signs’ of an appropriate number of entries in each
$(\ell _1,\ldots ,\ell _m)$
, we can closely couple the resulting random variables X (essentially, we just randomly ‘flip the signs’ of an appropriate number of entries in each
![]() $I_k$
). Note that the ‘balancedness’ conditions (c) and (d) in Lemma 11.1 ensure that the expected value of X does not depend strongly on the choice of
$I_k$
). Note that the ‘balancedness’ conditions (c) and (d) in Lemma 11.1 ensure that the expected value of X does not depend strongly on the choice of
![]() $(\ell _1,\ldots ,\ell _m)$
.
$(\ell _1,\ldots ,\ell _m)$
.
Lemma 11.2. Fix
![]() $0<\delta <1/4$
, and consider a partition
$0<\delta <1/4$
, and consider a partition
![]() $[n]=I_1\cup \cdots \cup I_m$
as in Lemma 11.1, as well as a symmetric matrix
$[n]=I_1\cup \cdots \cup I_m$
as in Lemma 11.1, as well as a symmetric matrix
![]() $F\in \mathbb {R}^{n\times n}$
, a vector
$F\in \mathbb {R}^{n\times n}$
, a vector
![]() $\vec f\in \mathbb {R}^{n}$
and a real number
$\vec f\in \mathbb {R}^{n}$
and a real number
![]() $f_0$
satisfying conditions (a–d). Assume that n is sufficiently large with respect to
$f_0$
satisfying conditions (a–d). Assume that n is sufficiently large with respect to
![]() $\delta $
.
$\delta $
.
Consider sequences
![]() $(\ell _1,\ldots ,\ell _m), (\ell _1',\ldots ,\ell _m')\in \mathbb {N}^{m}$
with
$(\ell _1,\ldots ,\ell _m), (\ell _1',\ldots ,\ell _m')\in \mathbb {N}^{m}$
with
![]() $|\ell _{k}-|I_k|/2|\le \sqrt {n^{1-\delta }}\log n$
and
$|\ell _{k}-|I_k|/2|\le \sqrt {n^{1-\delta }}\log n$
and
![]() $|\ell _{k}'-|I_k|/2|\le \sqrt {n^{1-\delta }}\log n$
for
$|\ell _{k}'-|I_k|/2|\le \sqrt {n^{1-\delta }}\log n$
for
![]() $k=1,\ldots ,m$
. Then, let
$k=1,\ldots ,m$
. Then, let
![]() $\vec {x}\in \{-1,1\}^{n}$
be a uniformly random vector such that
$\vec {x}\in \{-1,1\}^{n}$
be a uniformly random vector such that
![]() $\vec {x}_{I_{k}}$
has exactly
$\vec {x}_{I_{k}}$
has exactly
![]() $\ell _{k}$
ones for each
$\ell _{k}$
ones for each
![]() $k=1,\ldots ,m$
and let
$k=1,\ldots ,m$
and let
![]() $\vec {x}'\in \{-1,1\}^{n}$
be a uniformly random vector such that
$\vec {x}'\in \{-1,1\}^{n}$
be a uniformly random vector such that
![]() $\vec {x}^{\prime }_{I_{k}}$
has exactly
$\vec {x}^{\prime }_{I_{k}}$
has exactly
![]() $\ell _{k}'$
ones for each
$\ell _{k}'$
ones for each
![]() $k=1,\ldots ,m$
. Let
$k=1,\ldots ,m$
. Let
![]() $X= f_0+\vec f\cdot \vec {x}+\vec {x}^{\intercal }F\vec {x}$
and
$X= f_0+\vec f\cdot \vec {x}+\vec {x}^{\intercal }F\vec {x}$
and
![]() $X'=f_0+\vec f\cdot \vec {x}'+\vec {x}^{\prime \intercal }F\vec {x}'$
. Then we can couple
$X'=f_0+\vec f\cdot \vec {x}'+\vec {x}^{\prime \intercal }F\vec {x}'$
. Then we can couple
![]() $\vec {x}$
and
$\vec {x}$
and
![]() $\vec {x}'$
such that
$\vec {x}'$
such that
![]() $|X-X'|\le n^{3/4+4\delta }$
with probability at least
$|X-X'|\le n^{3/4+4\delta }$
with probability at least
![]() $1-\exp (-n^{\delta /2})$
.
$1-\exp (-n^{\delta /2})$
.
Proof. Let us couple the random vectors
![]() $\vec {x}$
and
$\vec {x}$
and
![]() $\vec {x}'$
in the following way. First, independently for each
$\vec {x}'$
in the following way. First, independently for each
![]() $k=1,\ldots ,m$
, let us choose a uniformly random subset
$k=1,\ldots ,m$
, let us choose a uniformly random subset
![]() $R_k\subseteq I_k$
of size
$R_k\subseteq I_k$
of size
![]() $|I_k|-2\lfloor |I_k|/2 - \sqrt {n^{1-\delta }}\log n\rfloor $
. Note that then
$|I_k|-2\lfloor |I_k|/2 - \sqrt {n^{1-\delta }}\log n\rfloor $
. Note that then
![]() $|I_k\setminus R_k|$
is even and
$|I_k\setminus R_k|$
is even and
![]() $2\sqrt {n^{1-\delta }}\log n\le |R_k|\le 3\sqrt {n^{1-\delta }}\log n$
. We also have
$2\sqrt {n^{1-\delta }}\log n\le |R_k|\le 3\sqrt {n^{1-\delta }}\log n$
. We also have
![]() $0\le \ell _k-|I_k\setminus R_k|/2\le |R_k|$
and
$0\le \ell _k-|I_k\setminus R_k|/2\le |R_k|$
and
![]() $0\le \ell _k'-|I_k\setminus R_k|/2\le |R_k|$
. Let us now sample
$0\le \ell _k'-|I_k\setminus R_k|/2\le |R_k|$
. Let us now sample
![]() $\vec {x}_{R_k}\in \{-1,1\}^{R_k}$
by taking a uniformly random vector with exactly
$\vec {x}_{R_k}\in \{-1,1\}^{R_k}$
by taking a uniformly random vector with exactly
![]() $\ell _{k}-|I_k\setminus R_k|/2$
ones, and independently let us sample
$\ell _{k}-|I_k\setminus R_k|/2$
ones, and independently let us sample
![]() $\vec {x}_{R_k}'\in \{-1,1\}^{R_k}$
by taking a uniformly random vector with exactly
$\vec {x}_{R_k}'\in \{-1,1\}^{R_k}$
by taking a uniformly random vector with exactly
![]() $\ell _{k}'-|I_k\setminus R_k|/2$
ones. Furthermore, let us sample a random vector in
$\ell _{k}'-|I_k\setminus R_k|/2$
ones. Furthermore, let us sample a random vector in
![]() $\{-1,1\}^{I_k\setminus R_k}$
with exactly
$\{-1,1\}^{I_k\setminus R_k}$
with exactly
![]() $|I_k\setminus R_k|/2$
ones and define both of
$|I_k\setminus R_k|/2$
ones and define both of
![]() $\vec {x}_{I_k\setminus R_k}$
and
$\vec {x}_{I_k\setminus R_k}$
and
![]() $\vec {x}_{I_k\setminus R_k}'$
to agree with this vector. After doing this for all
$\vec {x}_{I_k\setminus R_k}'$
to agree with this vector. After doing this for all
![]() $k=1,\ldots ,m$
, we have defined
$k=1,\ldots ,m$
, we have defined
![]() $\vec {x}$
and
$\vec {x}$
and
![]() $\vec {x}'$
with the appropriate number of ones in each index set
$\vec {x}'$
with the appropriate number of ones in each index set
![]() $I_k$
. For convenience, write
$I_k$
. For convenience, write
![]() $R=R_1\cup \cdots \cup R_k$
.
$R=R_1\cup \cdots \cup R_k$
.
We now need to check that
![]() $|X-X'|\le n^{3/4+4\delta }$
with probability at least
$|X-X'|\le n^{3/4+4\delta }$
with probability at least
![]() $1-\exp (-n^{\delta /2})$
. Since
$1-\exp (-n^{\delta /2})$
. Since
![]() $\vec {x}$
and
$\vec {x}$
and
![]() $\vec {x}'$
agree in all coordinates outside R, all terms that do not involve coordinates in R cancel out in
$\vec {x}'$
agree in all coordinates outside R, all terms that do not involve coordinates in R cancel out in
![]() $X-X'$
. We may therefore write
$X-X'$
. We may therefore write
![]() $X-X'=g_R(\vec {x})-g_R(\vec {x}')$
, where (using that F is symmetric)
$X-X'=g_R(\vec {x})-g_R(\vec {x}')$
, where (using that F is symmetric)
 $$ \begin{align} g_R(\vec{x}):=\sum_{i\in R}f_ix_i + \sum_{\substack{(i,j)\in [n]\\i\in R \text{ or }j\in R}} F_{i,j}x_ix_{j}=\sum_{i\in R}f_ix_i+\sum_{(i,j)\in R^2} F_{i,j}x_ix_{j}+2\sum_{i\not\in R}\sum_{j\in R} F_{i,j}x_ix_{j} \end{align} $$
$$ \begin{align} g_R(\vec{x}):=\sum_{i\in R}f_ix_i + \sum_{\substack{(i,j)\in [n]\\i\in R \text{ or }j\in R}} F_{i,j}x_ix_{j}=\sum_{i\in R}f_ix_i+\sum_{(i,j)\in R^2} F_{i,j}x_ix_{j}+2\sum_{i\not\in R}\sum_{j\in R} F_{i,j}x_ix_{j} \end{align} $$
(and similarly for
![]() $g_R(\vec {x}')$
). It suffices to prove that with probability at least
$g_R(\vec {x}')$
). It suffices to prove that with probability at least
![]() $1-\exp (-n^{\delta /2})/2$
we have
$1-\exp (-n^{\delta /2})/2$
we have
![]() $|g_R(\vec {x})|\le n^{3/4+4\delta }/2$
(then the same holds analogously for
$|g_R(\vec {x})|\le n^{3/4+4\delta }/2$
(then the same holds analogously for
![]() $|g_R(\vec {x'})|$
and overall we obtain
$|g_R(\vec {x'})|$
and overall we obtain
![]() $|X-X'|=|g_R(\vec {x})-g_R(\vec {x}')|\le n^{3/4+4\delta }$
with probability at least
$|X-X'|=|g_R(\vec {x})-g_R(\vec {x}')|\le n^{3/4+4\delta }$
with probability at least
![]() $1-\exp (-n^{\delta /2})$
).
$1-\exp (-n^{\delta /2})$
).
Let us first consider the first two summands on the right-hand side of (11.1). Their expectation is

Now, note that for each
![]() $k=1,\ldots ,m$
, the expectation
$k=1,\ldots ,m$
, the expectation
is the same for all indices
![]() $i\in I_k$
. Since
$i\in I_k$
. Since
![]() $\sum _{i\in I_k} f_i=0$
by condition (c), this means that the first summand on the right-hand side of (11.2) is zero. For the second summand in (11.2), note that for any
$\sum _{i\in I_k} f_i=0$
by condition (c), this means that the first summand on the right-hand side of (11.2) is zero. For the second summand in (11.2), note that for any
![]() $k,h\in [m]$
the expectation
$k,h\in [m]$
the expectation
has the same value
![]() $E_{k,h}$
for all indices
$E_{k,h}$
for all indices
![]() $i\in I_k$
and
$i\in I_k$
and
![]() $j\in I_h$
with
$j\in I_h$
with
![]() $i\neq j$
. For all
$i\neq j$
. For all
![]() $i\in I_k$
and
$i\in I_k$
and
![]() $j\in I_h$
, the magnitude of this expectation is at most
$j\in I_h$
, the magnitude of this expectation is at most
![]() $\Pr [i\in R]\le 3\sqrt {n^{1-\delta }}\log n/|I_k|\leq n^{-1/2+\delta }$
(noting that
$\Pr [i\in R]\le 3\sqrt {n^{1-\delta }}\log n/|I_k|\leq n^{-1/2+\delta }$
(noting that
![]() $|I_k|=n/m\geq n^{1-\delta }/2$
). By (d) we have
$|I_k|=n/m\geq n^{1-\delta }/2$
). By (d) we have
![]() $\sum _{i\in I_k}\sum _{j\in I_h} F_{i,j}=0$
, and so we can conclude that
$\sum _{i\in I_k}\sum _{j\in I_h} F_{i,j}=0$
, and so we can conclude that

where in the last step we used (b). Furthermore, note that
 $$ \begin{align} \sum_{i\in R}f_ix_i+\sum_{(i,j)\in R^2} F_{i,j}x_ix_{j}=\vec{f}\cdot \vec{x}_R+\vec{x}_R^{\intercal}F\vec{x}_R, \end{align} $$
$$ \begin{align} \sum_{i\in R}f_ix_i+\sum_{(i,j)\in R^2} F_{i,j}x_ix_{j}=\vec{f}\cdot \vec{x}_R+\vec{x}_R^{\intercal}F\vec{x}_R, \end{align} $$
where here by slight abuse of notation we consider
![]() $\vec {x}_R$
as a vector in
$\vec {x}_R$
as a vector in
![]() $\{-1,0,1\}^n$
given by extending
$\{-1,0,1\}^n$
given by extending
![]() $\vec {x}_R\in \{-1,1\}^R$
by zeroes for the coordinates outside R. Note that this describes a random vector in
$\vec {x}_R\in \{-1,1\}^R$
by zeroes for the coordinates outside R. Note that this describes a random vector in
![]() $\{-1,0,1\}^n$
such that for each set
$\{-1,0,1\}^n$
such that for each set
![]() $I_k$
for
$I_k$
for
![]() $k=1,\ldots ,m$
, exactly
$k=1,\ldots ,m$
, exactly
![]() $\ell _k\leq n^{1/2}$
entries are
$\ell _k\leq n^{1/2}$
entries are
![]() $1$
, exactly
$1$
, exactly
![]() $|I_k|-2\lfloor |I_k|/2 - \sqrt {n^{1-\delta }}\log n\rfloor -\ell _k\leq 3\sqrt {n^{1-\delta }}-\ell _k\log n\le n^{1/2}-\ell _k$
entries are
$|I_k|-2\lfloor |I_k|/2 - \sqrt {n^{1-\delta }}\log n\rfloor -\ell _k\leq 3\sqrt {n^{1-\delta }}-\ell _k\log n\le n^{1/2}-\ell _k$
entries are
![]() $-1$
and the remaining entries are
$-1$
and the remaining entries are
![]() $0$
. Note that for any two outcomes of such a random vector differing by switching two entries, the resulting values of
$0$
. Note that for any two outcomes of such a random vector differing by switching two entries, the resulting values of
![]() $\vec {f}\cdot \vec {x}_R+\vec {x}_R^{\intercal }F\vec {x}_R$
differ by at most
$\vec {f}\cdot \vec {x}_R+\vec {x}_R^{\intercal }F\vec {x}_R$
differ by at most
![]() $5n^{1/2+3\delta }$
(indeed, by (a) the linear term
$5n^{1/2+3\delta }$
(indeed, by (a) the linear term
![]() $\vec {f}\cdot \vec {x}_R$
differs by at most
$\vec {f}\cdot \vec {x}_R$
differs by at most
![]() $4\lVert f\rVert _{\infty }\leq 4n^{1/2+3\delta }$
, and by (b) the term
$4\lVert f\rVert _{\infty }\leq 4n^{1/2+3\delta }$
, and by (b) the term
![]() $\vec {x}_R^{\intercal }F\vec {x}_R$
differs by at most
$\vec {x}_R^{\intercal }F\vec {x}_R$
differs by at most
![]() $8|R|\leq n^{1/2+3\delta }$
). Thus, we can apply Lemma 4.17 and conclude that with probability at least
$8|R|\leq n^{1/2+3\delta }$
). Thus, we can apply Lemma 4.17 and conclude that with probability at least
![]() $1-2\exp (-n^{3/2+8\delta }/(16\cdot 2m\cdot n^{1/2}\cdot 25n^{1+6\delta }))\geq 1-2\exp (-n^{\delta }/800)$
the quantity in (11.3) differs from its expectation by at most
$1-2\exp (-n^{3/2+8\delta }/(16\cdot 2m\cdot n^{1/2}\cdot 25n^{1+6\delta }))\geq 1-2\exp (-n^{\delta }/800)$
the quantity in (11.3) differs from its expectation by at most
![]() $n^{3/4+4\delta }/4$
. Given the above bound for this expectation, we can conclude that with probability at least
$n^{3/4+4\delta }/4$
. Given the above bound for this expectation, we can conclude that with probability at least
![]() $1-2\exp (-n^{\delta }/800)$
,
$1-2\exp (-n^{\delta }/800)$
,
 $$ \begin{align} \left|\sum_{i\in R}f_ix_i+\sum_{(i,j)\in R^2} F_{i,j}x_ix_{j}\right|\le n^{3/4+4\delta}/3. \end{align} $$
$$ \begin{align} \left|\sum_{i\in R}f_ix_i+\sum_{(i,j)\in R^2} F_{i,j}x_ix_{j}\right|\le n^{3/4+4\delta}/3. \end{align} $$
It remains to bound the third summand on the right-hand side of (11.1).
In order to do so, we first claim that with probability at least
![]() $1-2n\exp (-n^{\delta }/256)$
for each
$1-2n\exp (-n^{\delta }/256)$
for each
![]() $i=1,\ldots ,n$
we have
$i=1,\ldots ,n$
we have
![]() $|\sum _{j\in R}2F_{i,j} x_j|\le n^{1/4+\delta }$
. Indeed, for any fixed i, the sum
$|\sum _{j\in R}2F_{i,j} x_j|\le n^{1/4+\delta }$
. Indeed, for any fixed i, the sum
![]() $\sum _{j\in R}2F_{i,j}x_j$
can be interpreted as a linear function (with coefficients bounded by
$\sum _{j\in R}2F_{i,j}x_j$
can be interpreted as a linear function (with coefficients bounded by
![]() $2$
in absolute value by (b)) of a random vector in
$2$
in absolute value by (b)) of a random vector in
![]() $\{-1,0,1\}^n$
such that for each set
$\{-1,0,1\}^n$
such that for each set
![]() $I_k$
for
$I_k$
for
![]() $k=1,\ldots ,m$
, exactly
$k=1,\ldots ,m$
, exactly
![]() $\ell _k\leq n^{1/2}$
entries are
$\ell _k\leq n^{1/2}$
entries are
![]() $1$
, exactly
$1$
, exactly
![]() $|I_k|-2\lfloor |I_k|/2 - \sqrt {n^{1-\delta }}\log n\rfloor -\ell _k\le n^{1/2}-\ell _k$
entries are
$|I_k|-2\lfloor |I_k|/2 - \sqrt {n^{1-\delta }}\log n\rfloor -\ell _k\le n^{1/2}-\ell _k$
entries are
![]() $-1$
, and the remaining entries are
$-1$
, and the remaining entries are
![]() $0$
. So for each
$0$
. So for each
![]() $i=1,\ldots ,n$
, by Lemma 4.17 (noting that
$i=1,\ldots ,n$
, by Lemma 4.17 (noting that
![]() $\mathbb {E}[\sum _{j\in R}F_{i,j} x_j]=0$
by (d)) we have
$\mathbb {E}[\sum _{j\in R}F_{i,j} x_j]=0$
by (d)) we have
![]() $|\sum _{j\in R}F_{i,j} x_j|\le n^{1/4+\delta }$
with probability at least
$|\sum _{j\in R}F_{i,j} x_j|\le n^{1/4+\delta }$
with probability at least
![]() $1-2\exp (-n^{1/2+2\delta }/(2m\cdot n^{1/2}\cdot 8^2))\geq 1-2\exp (-n^{\delta }/256)$
.
$1-2\exp (-n^{1/2+2\delta }/(2m\cdot n^{1/2}\cdot 8^2))\geq 1-2\exp (-n^{\delta }/256)$
.
Let us now condition on an outcome of R and
![]() $\vec {x}_R$
such that we have
$\vec {x}_R$
such that we have
![]() $|\sum _{j\in R}2F_{i,j} x_j|\le n^{1/4+\delta }$
for
$|\sum _{j\in R}2F_{i,j} x_j|\le n^{1/4+\delta }$
for
![]() $i=1,\ldots ,n$
. Note that
$i=1,\ldots ,n$
. Note that
 $$\begin{align*}2\sum_{i\not\in R}\sum_{j\in R} F_{i,j}x_ix_{j}=\sum_{i\not\in R}\left(\sum_{j\in R}2F_{i,j} x_j\right)x_i.\end{align*}$$
$$\begin{align*}2\sum_{i\not\in R}\sum_{j\in R} F_{i,j}x_ix_{j}=\sum_{i\not\in R}\left(\sum_{j\in R}2F_{i,j} x_j\right)x_i.\end{align*}$$
Subject to the randomness of the coordinates outside R (which are chosen to be half
![]() $1$
and half
$1$
and half
![]() $-1$
inside each set
$-1$
inside each set
![]() $I_k\setminus R_k$
for
$I_k\setminus R_k$
for
![]() $k=1,\ldots ,m$
), the expectation of this quantity is
$k=1,\ldots ,m$
), the expectation of this quantity is
![]() $0$
(since for each individual
$0$
(since for each individual
![]() $x_i$
with
$x_i$
with
![]() $i\in R$
we have
$i\in R$
we have
![]() $\mathbb {E}x_i=0$
). Furthermore, this quantity can be interpreted as a linear function of the entries
$\mathbb {E}x_i=0$
). Furthermore, this quantity can be interpreted as a linear function of the entries
![]() $x_i$
with
$x_i$
with
![]() $i\not \in R$
, with coefficients bounded in absolute value by
$i\not \in R$
, with coefficients bounded in absolute value by
![]() $n^{1/4+\delta }$
. Thus, by Lemma 4.17 we have
$n^{1/4+\delta }$
. Thus, by Lemma 4.17 we have
![]() $|2\sum _{i\not \in R}\sum _{j\in R} F_{i,j}x_ix_{j}|\leq n^{3/4+3\delta }$
with probability at least
$|2\sum _{i\not \in R}\sum _{j\in R} F_{i,j}x_ix_{j}|\leq n^{3/4+3\delta }$
with probability at least
![]() $1-2\exp (-n^{3/2+6\delta }/(2n\cdot 16n^{1/2+2\delta })\geq 1-2\exp (-n^{\delta })$
.
$1-2\exp (-n^{3/2+6\delta }/(2n\cdot 16n^{1/2+2\delta })\geq 1-2\exp (-n^{\delta })$
.
Combining this with (11.4) and (11.1), we conclude that
![]() $|g_R(\vec {x})|\leq n^{3/4+4\delta }/2$
with probability at least
$|g_R(\vec {x})|\leq n^{3/4+4\delta }/2$
with probability at least
![]() $1-2(n+2)\exp (-n^{\delta }/800)\geq 1-\exp (-n^{\delta /2})/2$
.
$1-2(n+2)\exp (-n^{\delta }/800)\geq 1-\exp (-n^{\delta /2})/2$
.
The following lemma gives a comparison between the random variable X in Lemma 11.1 and its ‘independent Rademacher analog’. This lemma is a simple consequence of Lemma 11.2 since a uniformly random vector
![]() $\vec {y}\in \{-1,1\}^n$
can be interpreted as a mixture of different Boolean slices.
$\vec {y}\in \{-1,1\}^n$
can be interpreted as a mixture of different Boolean slices.
Lemma 11.3. Fix
![]() $0<\delta <1/4$
, and consider a partition
$0<\delta <1/4$
, and consider a partition
![]() $[n]=I_1\cup \cdots \cup I_m$
as in Lemma 11.1, as well as a symmetric matrix
$[n]=I_1\cup \cdots \cup I_m$
as in Lemma 11.1, as well as a symmetric matrix
![]() $F\in \mathbb {R}^{n\times n}$
, a vector
$F\in \mathbb {R}^{n\times n}$
, a vector
![]() $\vec f\in \mathbb {R}^{n}$
and a real number
$\vec f\in \mathbb {R}^{n}$
and a real number
![]() $f_0$
satisfying conditions (a–d). Assume that n is sufficiently large with respect to
$f_0$
satisfying conditions (a–d). Assume that n is sufficiently large with respect to
![]() $\delta $
.
$\delta $
.
Consider a sequence
![]() $(\ell _1,\ldots ,\ell _m)\in \mathbb N^{m}$
with
$(\ell _1,\ldots ,\ell _m)\in \mathbb N^{m}$
with
![]() $|\ell _{k}-|I_k|/2|\le \sqrt {n^{1-\delta }}\log n$
and for
$|\ell _{k}-|I_k|/2|\le \sqrt {n^{1-\delta }}\log n$
and for
![]() $k=1,\ldots ,m$
, and let
$k=1,\ldots ,m$
, and let
![]() $\vec {x}\in \{-1,1\}^{n}$
be a uniformly random vector such that
$\vec {x}\in \{-1,1\}^{n}$
be a uniformly random vector such that
![]() $\vec {x}_{I_{k}}$
has exactly
$\vec {x}_{I_{k}}$
has exactly
![]() $\ell _{k}$
ones for each
$\ell _{k}$
ones for each
![]() $k=1,\ldots ,m$
. Furthermore let
$k=1,\ldots ,m$
. Furthermore let
![]() $\vec {y}\in \{-1,1\}^{n}$
be a uniformly random vector (with independent coordinates). Let
$\vec {y}\in \{-1,1\}^{n}$
be a uniformly random vector (with independent coordinates). Let
![]() $X=\vec f_0+f\cdot \vec {x}+\vec {x}^{\intercal }F\vec {x}$
and
$X=\vec f_0+f\cdot \vec {x}+\vec {x}^{\intercal }F\vec {x}$
and
![]() $Y=f_0+\vec f\cdot \vec {y}+\vec {y}^{\intercal }F\vec {y}$
. Then we can couple
$Y=f_0+\vec f\cdot \vec {y}+\vec {y}^{\intercal }F\vec {y}$
. Then we can couple
![]() $\vec {x}$
and
$\vec {x}$
and
![]() $\vec {y}$
such that
$\vec {y}$
such that
![]() $|X-Y|\le n^{3/4+4\delta }$
with probability at least
$|X-Y|\le n^{3/4+4\delta }$
with probability at least
![]() $1-\exp (-(\log n)^2/8)$
.
$1-\exp (-(\log n)^2/8)$
.
Proof. For
![]() $k=1,\ldots ,m$
, consider independent binomial random variables
$k=1,\ldots ,m$
, consider independent binomial random variables
![]() $\ell _k'\sim \mathrm {Bin}(|I_k|,1/2)$
. We can sample
$\ell _k'\sim \mathrm {Bin}(|I_k|,1/2)$
. We can sample
![]() $\vec {y}$
by taking a random vector in
$\vec {y}$
by taking a random vector in
![]() $\{-1,1\}^n$
with exactly
$\{-1,1\}^n$
with exactly
![]() $\ell _{k}'$
ones among the entries with indices in
$\ell _{k}'$
ones among the entries with indices in
![]() $I_k$
for each
$I_k$
for each
![]() $k=1,\ldots ,m$
. Note that altogether this gives precisely a uniformly random vector in
$k=1,\ldots ,m$
. Note that altogether this gives precisely a uniformly random vector in
![]() $\{-1,1\}^{n}$
.
$\{-1,1\}^{n}$
.
We now need to define the desired coupling of
![]() $\vec {x}$
and
$\vec {x}$
and
![]() $\vec {y}$
. By the Chernoff bound (see Lemma 4.16), with probability at least
$\vec {y}$
. By the Chernoff bound (see Lemma 4.16), with probability at least
![]() $1-4n^\delta \cdot \exp (-(\log n)^2/4)\le 1-\exp (-(\log n)^2/6)$
we have
$1-4n^\delta \cdot \exp (-(\log n)^2/4)\le 1-\exp (-(\log n)^2/6)$
we have
![]() $|\ell _{k}'-|I_k|/2|\le \sqrt {n^{1-\delta }}\log n$
for
$|\ell _{k}'-|I_k|/2|\le \sqrt {n^{1-\delta }}\log n$
for
![]() $k=1,\ldots ,m$
(here, we used that
$k=1,\ldots ,m$
(here, we used that
![]() $m\leq 2n^\delta $
and
$m\leq 2n^\delta $
and
![]() $|I_k|=n/m\le 2n^{1-\delta }$
). Whenever this is the case, then by Lemma 11.2 we can couple
$|I_k|=n/m\le 2n^{1-\delta }$
). Whenever this is the case, then by Lemma 11.2 we can couple
![]() $\vec x$
and
$\vec x$
and
![]() $\vec {y}$
in such a way that we have
$\vec {y}$
in such a way that we have
![]() $|X-Y|\le n^{3/4+4\delta }$
with probability at least
$|X-Y|\le n^{3/4+4\delta }$
with probability at least
![]() $1-\exp (-n^{\delta /2})$
. Otherwise, let us couple
$1-\exp (-n^{\delta /2})$
. Otherwise, let us couple
![]() $\vec x$
and
$\vec x$
and
![]() $\vec {y}$
arbitrarily.
$\vec {y}$
arbitrarily.
Now, the overall probability of having
![]() $|X-Y|\le n^{3/4+4\delta }$
is at least
$|X-Y|\le n^{3/4+4\delta }$
is at least
![]() $1-\exp (-(\log n)^2/6)-\exp (-n^{\delta /2})\geq 1-\exp (-(\log n)^2/8)$
, as desired.
$1-\exp (-(\log n)^2/6)-\exp (-n^{\delta /2})\geq 1-\exp (-(\log n)^2/8)$
, as desired.
In order to obtain the comparison of the characteristic functions of X and Z in Lemma 11.1(3), we will use Lemma 11.3 to relate X to Y. It then remains to compare the characteristic functions of Y and Z. To do so, we use the Gaussian invariance principle of Mossel, O’Donnell and Oleszkiewicz [Reference Mossel, O’Donnell and Oleszkiewicz74]. The version stated in Theorem 11.5 below is a special case of [Reference O’Donnell81, (11.29)].
Definition 11.4. Given a multilinear polynomial
![]() $g(x_1,\ldots ,x_n) = \sum _{S\subseteq [n]} a_S\prod _{i\in S}x_i$
, for
$g(x_1,\ldots ,x_n) = \sum _{S\subseteq [n]} a_S\prod _{i\in S}x_i$
, for
![]() $t=1,\ldots ,n$
the influence of the variable
$t=1,\ldots ,n$
the influence of the variable
![]() $x_t$
is defined as
$x_t$
is defined as
 $$\begin{align*}\operatorname{Inf}_t[g] = \sum_{\substack{S\subseteq [n]\\t\in S}} a_S^2.\end{align*}$$
$$\begin{align*}\operatorname{Inf}_t[g] = \sum_{\substack{S\subseteq [n]\\t\in S}} a_S^2.\end{align*}$$
Theorem 11.5. Let g be an n-variable multilinear polynomial of degree at most k. Let
![]() $\vec {y}\in \{-1,1\}^n$
be a uniformly random vector (i.e., a vector of independent Rademacher random variables), and let
$\vec {y}\in \{-1,1\}^n$
be a uniformly random vector (i.e., a vector of independent Rademacher random variables), and let
![]() $\vec {z}\sim \mathcal {N}(0,1)^{\otimes n}$
be a vector of independent standard Gaussian random variables. Then for any four-times-differentiable function
$\vec {z}\sim \mathcal {N}(0,1)^{\otimes n}$
be a vector of independent standard Gaussian random variables. Then for any four-times-differentiable function
![]() $\psi \colon \mathbb {R}\to \mathbb {R}$
, we have
$\psi \colon \mathbb {R}\to \mathbb {R}$
, we have
 $$\begin{align*}\Big|\mathbb{E}[\psi(g(\vec{y}))-\psi(g(\vec{z}))]\Big| \le \frac{9^k}{12}\cdot \lVert\psi^{(4)}\rVert_{\infty}\sum_{t=1}^n\operatorname{Inf}_t[g]^{2}.\end{align*}$$
$$\begin{align*}\Big|\mathbb{E}[\psi(g(\vec{y}))-\psi(g(\vec{z}))]\Big| \le \frac{9^k}{12}\cdot \lVert\psi^{(4)}\rVert_{\infty}\sum_{t=1}^n\operatorname{Inf}_t[g]^{2}.\end{align*}$$
As a simple consequence of Theorem 11.5, we obtain the following lemma.
Lemma 11.6. Fix
![]() $0<\delta <1/4$
. Consider a vector
$0<\delta <1/4$
. Consider a vector
![]() $\vec {f}\in \mathbb {R}^n$
with
$\vec {f}\in \mathbb {R}^n$
with
![]() $\lVert \vec {f}\rVert _{\infty }\le n^{1/2+3\delta }$
and a matrix
$\lVert \vec {f}\rVert _{\infty }\le n^{1/2+3\delta }$
and a matrix
![]() $F\in \mathbb {R}^{n\times n}$
with entries bounded in absolute value by 1, as well as a real number
$F\in \mathbb {R}^{n\times n}$
with entries bounded in absolute value by 1, as well as a real number
![]() $f_0$
. Assume that n is sufficiently large with respect to
$f_0$
. Assume that n is sufficiently large with respect to
![]() $\delta $
.
$\delta $
.
Let
![]() $\vec {y}\in \{-1,1\}^n$
be a uniformly random vector, and let
$\vec {y}\in \{-1,1\}^n$
be a uniformly random vector, and let
![]() $\vec {z}\sim \mathcal {N}(0,1)^{\otimes n}$
be a vector of independent standard Gaussian random variables. Let
$\vec {z}\sim \mathcal {N}(0,1)^{\otimes n}$
be a vector of independent standard Gaussian random variables. Let
![]() $Y = f_0+\vec {f}\cdot \vec {y} + \vec {y}^\intercal F\vec {y}$
and
$Y = f_0+\vec {f}\cdot \vec {y} + \vec {y}^\intercal F\vec {y}$
and
![]() $Z = f_0+\vec {f}\cdot \vec {z} + \vec {z}^\intercal F\vec {z}$
. Then for any four-times-differentiable function
$Z = f_0+\vec {f}\cdot \vec {z} + \vec {z}^\intercal F\vec {z}$
. Then for any four-times-differentiable function
![]() $\psi \colon \mathbb {R}\to \mathbb {R}$
, we have
$\psi \colon \mathbb {R}\to \mathbb {R}$
, we have
Proof. Let
![]() $F'$
be obtained from F by setting each diagonal entry to zero. Define the multilinear polynomial g by
$F'$
be obtained from F by setting each diagonal entry to zero. Define the multilinear polynomial g by
![]() $g(\vec {x}) = f_0+\vec {f}\cdot \vec {x} + \vec {x}^\intercal F'\vec {x} + \sum _{i}F_{i,i}$
, and let
$g(\vec {x}) = f_0+\vec {f}\cdot \vec {x} + \vec {x}^\intercal F'\vec {x} + \sum _{i}F_{i,i}$
, and let
![]() $Y' = g(\vec y)$
and
$Y' = g(\vec y)$
and
![]() $Z'=g(\vec z)$
. Note that
$Z'=g(\vec z)$
. Note that
![]() $\operatorname {Inf}_t[g]\le (n^{1/2+3\delta })^2 + n \le 2n^{1+6\delta }$
for
$\operatorname {Inf}_t[g]\le (n^{1/2+3\delta })^2 + n \le 2n^{1+6\delta }$
for
![]() $t=1,\ldots ,n$
, so
$t=1,\ldots ,n$
, so
![]() $\sum _{t=1}^{n}\operatorname {Inf}_t[g]^{2}\le 4n^{3+12\delta }$
. Theorem 11.5 then implies that
$\sum _{t=1}^{n}\operatorname {Inf}_t[g]^{2}\le 4n^{3+12\delta }$
. Theorem 11.5 then implies that
Furthermore, we always have
![]() $y_i^2 = 1$
for
$y_i^2 = 1$
for
![]() $i=1,\ldots ,n$
, meaning that
$i=1,\ldots ,n$
, meaning that
![]() $Y' = Y$
and in particular
$Y' = Y$
and in particular
![]() $\mathbb {E}[\psi (Y')-\psi (Y)]=0$
. By the Cauchy–Schwarz inequality, we also have
$\mathbb {E}[\psi (Y')-\psi (Y)]=0$
. By the Cauchy–Schwarz inequality, we also have
 $$ \begin{align*}|\mathbb{E}[\psi(Z')-\psi(Z)]|\le \mathbb{E}|\psi(Z')-\psi(Z)|\le \lVert\psi'\rVert_{\infty}\cdot \mathbb{E}|Z'-Z|&\le \lVert\psi'\rVert_{\infty}\cdot (\mathbb{E}[(Z'-Z)^2])^{1/2}\\ &\le 2\lVert\psi'\rVert_{\infty}n^{1/2}, \end{align*} $$
$$ \begin{align*}|\mathbb{E}[\psi(Z')-\psi(Z)]|\le \mathbb{E}|\psi(Z')-\psi(Z)|\le \lVert\psi'\rVert_{\infty}\cdot \mathbb{E}|Z'-Z|&\le \lVert\psi'\rVert_{\infty}\cdot (\mathbb{E}[(Z'-Z)^2])^{1/2}\\ &\le 2\lVert\psi'\rVert_{\infty}n^{1/2}, \end{align*} $$
where we used
![]() $\mathbb {E}[(Z'-Z)^2]=\mathbb {E}[(F_{1,1}(z_1^2-1)+\cdots +F_{n,n}(z_n^2-1))^2]=2|F_{1,1}|^2+\cdots +2|F_{n,n}|^2\le 2n$
in the last step. Combining these estimates gives the desired result.
$\mathbb {E}[(Z'-Z)^2]=\mathbb {E}[(F_{1,1}(z_1^2-1)+\cdots +F_{n,n}(z_n^2-1))^2]=2|F_{1,1}|^2+\cdots +2|F_{n,n}|^2\le 2n$
in the last step. Combining these estimates gives the desired result.
Let us now prove Lemma 11.1.
Proof of Lemma 11.1
We may assume that n is sufficiently large with respect to
![]() $\delta $
. Let
$\delta $
. Let
![]() $\vec {y}\in \{-1,1\}^n$
be a uniformly random vector, and define
$\vec {y}\in \{-1,1\}^n$
be a uniformly random vector, and define
![]() $Y=f_0+\vec f\cdot \vec {y}+\vec {y}^{\intercal }F\vec {y}$
. By Lemma 11.3, we can couple
$Y=f_0+\vec f\cdot \vec {y}+\vec {y}^{\intercal }F\vec {y}$
. By Lemma 11.3, we can couple
![]() $\vec {x}$
and
$\vec {x}$
and
![]() $\vec {y}$
such that
$\vec {y}$
such that
![]() $|X-Y|\le n^{3/4+4\delta }$
with probability at least
$|X-Y|\le n^{3/4+4\delta }$
with probability at least
![]() $1-\exp (-(\log n)^2/8)$
.
$1-\exp (-(\log n)^2/8)$
.
We can now compute
![]() $\mathbb {E}Y=\mathbb {E}Z=f_0+\sum _{i=1}^{n}F_{i,i}$
. Furthermore, since
$\mathbb {E}Y=\mathbb {E}Z=f_0+\sum _{i=1}^{n}F_{i,i}$
. Furthermore, since
![]() $|X-Y|\lesssim n^{2}$
always holds, we have
$|X-Y|\lesssim n^{2}$
always holds, we have
![]() $|\mathbb {E}X-\mathbb {E}Y|\le \mathbb {E}|X-Y|\lesssim n^{3/4+4\delta }+\exp (-(\log n)^2/8)\cdot n^{2}\lesssim n^{3/4+4\delta }$
and therefore
$|\mathbb {E}X-\mathbb {E}Y|\le \mathbb {E}|X-Y|\lesssim n^{3/4+4\delta }+\exp (-(\log n)^2/8)\cdot n^{2}\lesssim n^{3/4+4\delta }$
and therefore
![]() $\mathbb {E}X=f_0+\sum _{i=1}^{n}F_{i,i}+O(n^{3/4+4\delta })$
. This proves (1).
$\mathbb {E}X=f_0+\sum _{i=1}^{n}F_{i,i}+O(n^{3/4+4\delta })$
. This proves (1).
Note that
![]() $Y-\mathbb {E}Y=\vec {f}\cdot \vec {y}+\sum _{i<j} 2F_{i,j}y_iy_j$
(here, we are using that
$Y-\mathbb {E}Y=\vec {f}\cdot \vec {y}+\sum _{i<j} 2F_{i,j}y_iy_j$
(here, we are using that
![]() $y_i^2=1$
and that F is symmetric). Therefore, (4.5) gives
$y_i^2=1$
and that F is symmetric). Therefore, (4.5) gives
![]() $\sigma (Y)^2=\lVert \vec {f}\rVert _2^2+\sum _{i<j} 4F_{i,j}^2=2\lVert F\rVert _{\mathrm F}^2+\lVert \vec {f}\rVert _2^2-2\sum _{i=1}^{n}F_{i,i}^2=2\lVert F\rVert _{\mathrm F}^2+\lVert \vec {f}\rVert _2^2+O(n)$
(and so in particular
$\sigma (Y)^2=\lVert \vec {f}\rVert _2^2+\sum _{i<j} 4F_{i,j}^2=2\lVert F\rVert _{\mathrm F}^2+\lVert \vec {f}\rVert _2^2-2\sum _{i=1}^{n}F_{i,i}^2=2\lVert F\rVert _{\mathrm F}^2+\lVert \vec {f}\rVert _2^2+O(n)$
(and so in particular
![]() $\sigma (Y)^2\lesssim n^{2+6\delta }$
). Furthermore (using the Cauchy–Schwarz inequality), we have
$\sigma (Y)^2\lesssim n^{2+6\delta }$
). Furthermore (using the Cauchy–Schwarz inequality), we have
 $$ \begin{align*} &|\sigma(X)^2-\sigma(Y)^2|\\ &\qquad=\left|\mathbb{E}\left[(X-\mathbb{E}X)^2-(Y-\mathbb{E}Y)^2\right]\right|\le \mathbb{E}\left[|X-Y-\mathbb{E}X+\mathbb{E}Y|\cdot |X+Y-\mathbb{E}X-\mathbb{E}Y|\right]\\ &\qquad\le\left(\mathbb{E}\left[(|X-Y|+|\mathbb{E}X-\mathbb{E}Y|)^2\right]\right)^{1/2}\cdot \left(\mathbb{E}\left[(|X-\mathbb{E}X|+|Y-\mathbb{E}Y|)^2\right]\right)^{1/2}\\ &\qquad\le\left(\mathbb{E}\left[(|X-Y|+O(n^{3/4+4\delta}))^2\right]\right)^{1/2}\cdot \left(2\mathbb{E}\left[|X-\mathbb{E}X|^2\right]+2\mathbb{E}\left[|Y-\mathbb{E}Y|^2\right]\right)^{1/2}\\ &\qquad\lesssim \left(\mathbb{E}[|X-Y|^2] +\mathbb{E}|X-Y|\cdot O(n^{3/4+4\delta})+O(n^{3/2+8\delta})\right)^{1/2}\cdot \left(\sigma(X)^2+\sigma(Y)^2\right)^{1/2}\\ &\qquad\lesssim \left(n^{3/2+8\delta}+\exp(-(\log n)^2/8)\cdot n^{4} +O(n^{3/2+8\delta})\right)^{1/2}\cdot (\sigma(X)+\sigma(Y))\\ &\qquad\lesssim n^{3/4+4\delta}\cdot (\sigma(X)+\sigma(Y)). \end{align*} $$
$$ \begin{align*} &|\sigma(X)^2-\sigma(Y)^2|\\ &\qquad=\left|\mathbb{E}\left[(X-\mathbb{E}X)^2-(Y-\mathbb{E}Y)^2\right]\right|\le \mathbb{E}\left[|X-Y-\mathbb{E}X+\mathbb{E}Y|\cdot |X+Y-\mathbb{E}X-\mathbb{E}Y|\right]\\ &\qquad\le\left(\mathbb{E}\left[(|X-Y|+|\mathbb{E}X-\mathbb{E}Y|)^2\right]\right)^{1/2}\cdot \left(\mathbb{E}\left[(|X-\mathbb{E}X|+|Y-\mathbb{E}Y|)^2\right]\right)^{1/2}\\ &\qquad\le\left(\mathbb{E}\left[(|X-Y|+O(n^{3/4+4\delta}))^2\right]\right)^{1/2}\cdot \left(2\mathbb{E}\left[|X-\mathbb{E}X|^2\right]+2\mathbb{E}\left[|Y-\mathbb{E}Y|^2\right]\right)^{1/2}\\ &\qquad\lesssim \left(\mathbb{E}[|X-Y|^2] +\mathbb{E}|X-Y|\cdot O(n^{3/4+4\delta})+O(n^{3/2+8\delta})\right)^{1/2}\cdot \left(\sigma(X)^2+\sigma(Y)^2\right)^{1/2}\\ &\qquad\lesssim \left(n^{3/2+8\delta}+\exp(-(\log n)^2/8)\cdot n^{4} +O(n^{3/2+8\delta})\right)^{1/2}\cdot (\sigma(X)+\sigma(Y))\\ &\qquad\lesssim n^{3/4+4\delta}\cdot (\sigma(X)+\sigma(Y)). \end{align*} $$
Hence,
![]() $|\sigma (X)-\sigma (Y)|\lesssim n^{3/4+4\delta }$
and in particular
$|\sigma (X)-\sigma (Y)|\lesssim n^{3/4+4\delta }$
and in particular
![]() $\sigma (X)\leq \sigma (Y)+O(n^{3/4+4\delta })\lesssim n^{1+3\delta }$
. Thus, we obtain
$\sigma (X)\leq \sigma (Y)+O(n^{3/4+4\delta })\lesssim n^{1+3\delta }$
. Thus, we obtain
![]() $|\sigma (X)^2-\sigma (Y)^2|= |\sigma (X)-\sigma (Y)| (\sigma (X)+\sigma (Y))\lesssim n^{3/4+4\delta } \cdot n^{1+3\delta }=n^{7/4+7\delta }$
. This gives
$|\sigma (X)^2-\sigma (Y)^2|= |\sigma (X)-\sigma (Y)| (\sigma (X)+\sigma (Y))\lesssim n^{3/4+4\delta } \cdot n^{1+3\delta }=n^{7/4+7\delta }$
. This gives
![]() $\sigma (X)^2=\sigma (Y)^2+O(n^{7/4+7\delta })=2\lVert F\rVert _{\mathrm F}^2+\lVert \vec {f}\rVert _2^2+O(n^{7/4+7\delta })$
.
$\sigma (X)^2=\sigma (Y)^2+O(n^{7/4+7\delta })=2\lVert F\rVert _{\mathrm F}^2+\lVert \vec {f}\rVert _2^2+O(n^{7/4+7\delta })$
.
To finish the proof of (2), we observe that
![]() $Z-\mathbb {E}Z=\vec {f}\cdot \vec {z}+\sum _{i=1}^{n} F_{i,i}(z_i^2-1)+\sum _{i<j} 2F_{i,j}z_iz_j$
, so we can compute
$Z-\mathbb {E}Z=\vec {f}\cdot \vec {z}+\sum _{i=1}^{n} F_{i,i}(z_i^2-1)+\sum _{i<j} 2F_{i,j}z_iz_j$
, so we can compute
![]() $\sigma (Z)^2=\lVert \vec {f}\rVert _2^2+\sum _{i=1}^{n} 2F_{i,i}^2+\sum _{i<j}(2F_{i,j})^2=2\lVert F\rVert _{\mathrm F}^2+\lVert \vec {f}\rVert _2^2$
.
$\sigma (Z)^2=\lVert \vec {f}\rVert _2^2+\sum _{i=1}^{n} 2F_{i,i}^2+\sum _{i<j}(2F_{i,j})^2=2\lVert F\rVert _{\mathrm F}^2+\lVert \vec {f}\rVert _2^2$
.
For (3), consider some
![]() $\tau \in \mathbb {R}$
. We have
$\tau \in \mathbb {R}$
. We have
 $$ \begin{align*} |\varphi_Y(\tau)-\varphi_Z(\tau)|&=\Big|\mathbb{E}[\exp(i\tau Y)-\exp(i\tau Z)]\Big|=\Big|\mathbb{E}[\cos(\tau Y)+i\sin(\tau Y)-\cos(\tau Z)-i\sin(\tau Z)]\Big|\\ &\le \Big|\mathbb{E}[\cos(\tau Y)-\cos(\tau Z)]\Big|+\Big|\mathbb{E}[\sin(\tau Y)-\sin(\tau Z)]\Big|\Big|\\ &\lesssim |\tau|^4\cdot n^{3+12\delta} + |\tau|\cdot n^{1/2}, \end{align*} $$
$$ \begin{align*} |\varphi_Y(\tau)-\varphi_Z(\tau)|&=\Big|\mathbb{E}[\exp(i\tau Y)-\exp(i\tau Z)]\Big|=\Big|\mathbb{E}[\cos(\tau Y)+i\sin(\tau Y)-\cos(\tau Z)-i\sin(\tau Z)]\Big|\\ &\le \Big|\mathbb{E}[\cos(\tau Y)-\cos(\tau Z)]\Big|+\Big|\mathbb{E}[\sin(\tau Y)-\sin(\tau Z)]\Big|\Big|\\ &\lesssim |\tau|^4\cdot n^{3+12\delta} + |\tau|\cdot n^{1/2}, \end{align*} $$
where in the last step we applied Lemma 11.6 to the functions
![]() $u\mapsto \cos (\tau u)$
and
$u\mapsto \cos (\tau u)$
and
![]() $u\mapsto \sin (\tau u)$
. We furthermore have
$u\mapsto \sin (\tau u)$
. We furthermore have
 $$ \begin{align*} |\varphi_X(\tau)-\varphi_Y(\tau)|&=\Big|\mathbb{E}[\exp(i\tau X)-\exp(i\tau Y)]\Big|\\ &\le \mathbb{E}\Big[|\exp(i\tau X)-\exp(i\tau Y)|\Big] \le |\tau|\cdot \mathbb{E}[|X-Y|]\lesssim |\tau| \cdot n^{3/4+4\delta},\end{align*} $$
$$ \begin{align*} |\varphi_X(\tau)-\varphi_Y(\tau)|&=\Big|\mathbb{E}[\exp(i\tau X)-\exp(i\tau Y)]\Big|\\ &\le \mathbb{E}\Big[|\exp(i\tau X)-\exp(i\tau Y)|\Big] \le |\tau|\cdot \mathbb{E}[|X-Y|]\lesssim |\tau| \cdot n^{3/4+4\delta},\end{align*} $$
using that the absolute value of the derivative of the function
![]() $u\mapsto \exp (i\tau u)$
is bounded by
$u\mapsto \exp (i\tau u)$
is bounded by
![]() $|\tau |$
. Combining these two bounds using the triangle inequality gives (3).
$|\tau |$
. Combining these two bounds using the triangle inequality gives (3).
12 Short interval control in the additively structured case
Recall the definition of
![]() $\gamma $
-structuredness from Definition 9.1, and recall that in Section 9 we fixed
$\gamma $
-structuredness from Definition 9.1, and recall that in Section 9 we fixed
![]() $\gamma =10^{-4}$
and proved Theorem 3.1 in the case where
$\gamma =10^{-4}$
and proved Theorem 3.1 in the case where
![]() $(G,\vec e)$
is
$(G,\vec e)$
is
![]() $\gamma $
-unstructured. In this section, we finally prove Theorem 3.1 in the complementary case where
$\gamma $
-unstructured. In this section, we finally prove Theorem 3.1 in the complementary case where
![]() $(G,\vec e)$
is
$(G,\vec e)$
is
![]() $\gamma $
-structured.
$\gamma $
-structured.
As outlined in Section 3, the idea is as follows. First, we apply Lemma 4.12 to the vector
![]() $\vec {d}$
in Definition 9.1 to divide the vertex set into ‘buckets’ such that the
$\vec {d}$
in Definition 9.1 to divide the vertex set into ‘buckets’ such that the
![]() $d_v$
in each bucket have similar values. We encode the number of vertices in each bucket as a vector
$d_v$
in each bucket have similar values. We encode the number of vertices in each bucket as a vector
![]() $\vec \Delta $
; if we condition on an outcome of
$\vec \Delta $
; if we condition on an outcome of
![]() $\vec \Delta $
, then we can use the machinery developed in the previous sections to prove upper and lower bounds on the conditional small-ball probabilities of X. Then, we need to average these estimates over
$\vec \Delta $
, then we can use the machinery developed in the previous sections to prove upper and lower bounds on the conditional small-ball probabilities of X. Then, we need to average these estimates over
![]() $\vec \Delta $
. For this averaging, it is important that our conditional small-ball probabilities decay as we vary
$\vec \Delta $
. For this averaging, it is important that our conditional small-ball probabilities decay as we vary
![]() $\vec \Delta $
(this is where we need the nonuniform anticoncentration estimates in Theorem 5.2(1) and Lemma 6.2).
$\vec \Delta $
(this is where we need the nonuniform anticoncentration estimates in Theorem 5.2(1) and Lemma 6.2).
This section mostly consists of combining ingredients from previous sections, but there are still a few technical difficulties remaining. Chief among these is the fact that, as we vary the numbers of vertices in each bucket, the conditional expected value and variance of X fluctuate fairly significantly. We need to keep track of these fluctuations and ensure that they do not correlate adversarially with each other.
Proof of Theorem 3.1 in the
 $\gamma $
-structured case
$\gamma $
-structured case
Recall that G is a C-Ramsey graph with n vertices,
![]() $e_0\in \mathbb {R}$
and
$e_0\in \mathbb {R}$
and
![]() $\vec {e}\in \mathbb {R}^{V(G)}$
is a vector satisfying
$\vec {e}\in \mathbb {R}^{V(G)}$
is a vector satisfying
![]() $0\leq e_v\leq Hn$
for all
$0\leq e_v\leq Hn$
for all
![]() $v\in V(G)$
and that
$v\in V(G)$
and that
![]() $U\subseteq V(G)$
is a uniformly random vertex subset and
$U\subseteq V(G)$
is a uniformly random vertex subset and
![]() $X=e(G[U])+\sum _{v\in U}e_v+e_0$
. We may assume that n is sufficiently large with respect to
$X=e(G[U])+\sum _{v\in U}e_v+e_0$
. We may assume that n is sufficiently large with respect to
![]() $C, H$
and A.
$C, H$
and A.
Step 1: Bucketing setup. As in Definition 9.1, define
![]() $\vec {d}\in \mathbb {R}^{V(G)}$
by
$\vec {d}\in \mathbb {R}^{V(G)}$
by
![]() $d_v=e_v+\deg _G(v)/2$
for all
$d_v=e_v+\deg _G(v)/2$
for all
![]() $v\in V(G)$
. We are assuming that
$v\in V(G)$
. We are assuming that
![]() $(G,\vec e)$
is
$(G,\vec e)$
is
![]() $\gamma $
-structured, meaning that
$\gamma $
-structured, meaning that
![]() $\widehat {D}_{L,\gamma }(\vec {d})\le n^{1/2}$
, where
$\widehat {D}_{L,\gamma }(\vec {d})\le n^{1/2}$
, where
![]() $L=\lceil 100/\gamma \rceil =10^6$
(recall that
$L=\lceil 100/\gamma \rceil =10^6$
(recall that
![]() $\gamma =10^{-4}$
).
$\gamma =10^{-4}$
).
Note that
![]() $\lVert \vec {d}\rVert _{\infty }\le (H+1)n$
. Furthermore, for any subset
$\lVert \vec {d}\rVert _{\infty }\le (H+1)n$
. Furthermore, for any subset
![]() $S\subseteq V(G)$
of size
$S\subseteq V(G)$
of size
![]() $|S|=\lceil n^{1-\gamma }\rceil $
, we have
$|S|=\lceil n^{1-\gamma }\rceil $
, we have
![]() $\lVert \vec {d}_S\rVert _2\gtrsim _H n^{3/2-3\gamma /2}$
by Lemma 7.3 and therefore in particular
$\lVert \vec {d}_S\rVert _2\gtrsim _H n^{3/2-3\gamma /2}$
by Lemma 7.3 and therefore in particular
![]() $\lVert \vec {d}_S\rVert _2\ge n^{3/2-2\gamma }$
. Thus, we can apply Lemma 4.12 and obtain a partition
$\lVert \vec {d}_S\rVert _2\ge n^{3/2-2\gamma }$
. Thus, we can apply Lemma 4.12 and obtain a partition
![]() $V(G)=R\cup (I_1\cup \cdots \cup I_m)$
and real numbers
$V(G)=R\cup (I_1\cup \cdots \cup I_m)$
and real numbers
![]() $\kappa _1,\ldots ,\kappa _m\geq 0$
with
$\kappa _1,\ldots ,\kappa _m\geq 0$
with
![]() $|R|\le n^{1-\gamma }$
and
$|R|\le n^{1-\gamma }$
and
![]() $|I_1|=\cdots =|I_m|=\lceil n^{1-2\gamma }\rceil $
such that
$|I_1|=\cdots =|I_m|=\lceil n^{1-2\gamma }\rceil $
such that
![]() $|d_v-\kappa _k|\leq n^{1/2+4\gamma }$
for all
$|d_v-\kappa _k|\leq n^{1/2+4\gamma }$
for all
![]() $k=1,\ldots ,m$
and
$k=1,\ldots ,m$
and
![]() $v\in I_k$
. Let
$v\in I_k$
. Let
![]() $V=I_{1}\cup \cdots \cup I_{m}=V(G)\setminus R$
.
$V=I_{1}\cup \cdots \cup I_{m}=V(G)\setminus R$
.
Since
![]() $|R|\le n^{1-\gamma }$
, we have
$|R|\le n^{1-\gamma }$
, we have
![]() $2n/3\leq |V|\le n$
(i.e.,
$2n/3\leq |V|\le n$
(i.e.,
![]() $|V|$
is of order n) and thus furthermore
$|V|$
is of order n) and thus furthermore
![]() $|V|^{2\gamma }/2\le n^{2\gamma }/2\le m\le 2^{1-2\gamma }n^{2\gamma }\leq 2|V|^{2\gamma }$
(which means that we can apply Lemma 10.1 and 11.1 to the partition
$|V|^{2\gamma }/2\le n^{2\gamma }/2\le m\le 2^{1-2\gamma }n^{2\gamma }\leq 2|V|^{2\gamma }$
(which means that we can apply Lemma 10.1 and 11.1 to the partition
![]() $V=I_1\cup \cdots \cup I_m$
).
$V=I_1\cup \cdots \cup I_m$
).
In the next step of the proof, we will condition on an outcome of
![]() $U\cap R$
, and from then on we will only use the randomness of
$U\cap R$
, and from then on we will only use the randomness of
![]() $U\cap (I_1\cup \cdots \cup I_m)=U\cap V$
.
$U\cap (I_1\cup \cdots \cup I_m)=U\cap V$
.
Step 2: Conditioning on an outcome of
![]() $U\cap R$
. Recall that
$U\cap R$
. Recall that
![]() $U\subseteq V(G)$
is a random subset obtained by including each vertex with probability
$U\subseteq V(G)$
is a random subset obtained by including each vertex with probability
![]() $1/2$
independently. Let
$1/2$
independently. Let
![]() $x_{v}=1$
if
$x_{v}=1$
if
![]() $v\in U$
and
$v\in U$
and
![]() $x_{v}=-1$
if
$x_{v}=-1$
if
![]() $v\notin U$
, so the
$v\notin U$
, so the
![]() $x_{v}$
are independent Rademacher random variables. Then, as in (3.1) and the proof of Lemma 7.1 our random variable
$x_{v}$
are independent Rademacher random variables. Then, as in (3.1) and the proof of Lemma 7.1 our random variable
![]() $X=e(G[U])+\sum _{v\in U}e_v+e_0$
can be expressed as
$X=e(G[U])+\sum _{v\in U}e_v+e_0$
can be expressed as
 $$ \begin{align} \mathbb E X+\frac{1}{2}\sum_{v\in V(G)}\left(e_{v}+\frac{1}{2}\deg_{G}(v)\right)x_{v}+\frac{1}{4}\sum_{uv\in E(G)}x_{u}x_{v}=\mathbb E X+\frac{1}{2}\sum_{v\in V(G)}d_vx_{v}+\frac{1}{4}\sum_{uv\in E(G)}x_{u}x_{v}. \end{align} $$
$$ \begin{align} \mathbb E X+\frac{1}{2}\sum_{v\in V(G)}\left(e_{v}+\frac{1}{2}\deg_{G}(v)\right)x_{v}+\frac{1}{4}\sum_{uv\in E(G)}x_{u}x_{v}=\mathbb E X+\frac{1}{2}\sum_{v\in V(G)}d_vx_{v}+\frac{1}{4}\sum_{uv\in E(G)}x_{u}x_{v}. \end{align} $$
Let us now write
![]() $\vec {x}$
for the vector
$\vec {x}$
for the vector
![]() $(x_{v})_{v\in V}$
; we emphasize that this does not include the indices in R. We first rewrite (12.1) as a quadratic polynomial in
$(x_{v})_{v\in V}$
; we emphasize that this does not include the indices in R. We first rewrite (12.1) as a quadratic polynomial in
![]() $\vec {x}$
(where we view the random variables
$\vec {x}$
(where we view the random variables
![]() $x_{u}$
for
$x_{u}$
for
![]() $u\in R=V(G)\setminus V$
as being part of the coefficients of this quadratic polynomial). To this end, let
$u\in R=V(G)\setminus V$
as being part of the coefficients of this quadratic polynomial). To this end, let
![]() $M\in \{0,1\}^{V\times V}$
be the adjacency matrix of
$M\in \{0,1\}^{V\times V}$
be the adjacency matrix of
![]() $G[V]$
, and also define
$G[V]$
, and also define
 $$\begin{align*}y_{v}=d_{v}+\frac{1}{2}\sum_{\substack{u\in R\\uv\in E(G)}}x_{u}~\text{for }v\in V\quad\quad\text{and}\quad\quad E=\mathbb E X+\frac{1}{2}\sum_{v\in R}d_vx_v+\frac{1}{4}\sum_{uv\in E(G[R])}x_{u}x_{v}.\end{align*}$$
$$\begin{align*}y_{v}=d_{v}+\frac{1}{2}\sum_{\substack{u\in R\\uv\in E(G)}}x_{u}~\text{for }v\in V\quad\quad\text{and}\quad\quad E=\mathbb E X+\frac{1}{2}\sum_{v\in R}d_vx_v+\frac{1}{4}\sum_{uv\in E(G[R])}x_{u}x_{v}.\end{align*}$$
Then
Since
![]() $|R|\le n^{1-\gamma }$
and
$|R|\le n^{1-\gamma }$
and
![]() $0\leq d_v\leq Hn+n/2\leq (H+1)n$
for all
$0\leq d_v\leq Hn+n/2\leq (H+1)n$
for all
![]() $v\in V(G)$
, Theorem 4.15 (concentration via hypercontractivity) in combination with (4.5) shows that with probability at least
$v\in V(G)$
, Theorem 4.15 (concentration via hypercontractivity) in combination with (4.5) shows that with probability at least
![]() $1-\exp (-\Omega _H(n^{\gamma /2}))$
(over the randomness of
$1-\exp (-\Omega _H(n^{\gamma /2}))$
(over the randomness of
![]() $x_u$
for
$x_u$
for
![]() $u\in R$
) we have
$u\in R$
) we have
 $$\begin{align*}\bigg|\sum_{\substack{u\in R\\uv\in E(G)}}x_{u}\bigg|\le n^{1/2}~\text{for each }v\in V,\qquad\bigg|\sum_{uv\in E(G[R])}x_{u}x_{v}\bigg|\le n, \qquad \bigg|\sum_{v\in R}d_vx_{v}\bigg|\le n^{3/2}/2,\end{align*}$$
$$\begin{align*}\bigg|\sum_{\substack{u\in R\\uv\in E(G)}}x_{u}\bigg|\le n^{1/2}~\text{for each }v\in V,\qquad\bigg|\sum_{uv\in E(G[R])}x_{u}x_{v}\bigg|\le n, \qquad \bigg|\sum_{v\in R}d_vx_{v}\bigg|\le n^{3/2}/2,\end{align*}$$
which implies that
![]() $|E-\mathbb E X|\le n^{3/2}$
and
$|E-\mathbb E X|\le n^{3/2}$
and
![]() $|y_{v}-d_v|\le n^{1/2}$
for all
$|y_{v}-d_v|\le n^{1/2}$
for all
![]() $v\in V$
. For the rest of the proof, we implicitly condition on an outcome of
$v\in V$
. For the rest of the proof, we implicitly condition on an outcome of
![]() $U\cap R$
satisfying these properties, and we treat E and
$U\cap R$
satisfying these properties, and we treat E and
![]() $\vec {y}=(y_{v})_{v\in V}$
as being nonrandom objects.
$\vec {y}=(y_{v})_{v\in V}$
as being nonrandom objects.
Note that
![]() $\lVert \vec {y}\rVert _{\infty }\leq Hn+n/2+n^{1/2}\leq (H+2)n$
and
$\lVert \vec {y}\rVert _{\infty }\leq Hn+n/2+n^{1/2}\leq (H+2)n$
and
![]() $\lVert \vec {y}\rVert _2\geq \lVert \vec {d}_V\rVert _2-\lVert \vec {y}-d_V\rVert _2\geq \lVert \vec {d}_V\rVert _2-n$
. Furthermore, we have
$\lVert \vec {y}\rVert _2\geq \lVert \vec {d}_V\rVert _2-\lVert \vec {y}-d_V\rVert _2\geq \lVert \vec {d}_V\rVert _2-n$
. Furthermore, we have
![]() $\lVert \vec {d}_V\rVert _2\gtrsim _C n^{3/2}$
by Lemma 7.3 and therefore
$\lVert \vec {d}_V\rVert _2\gtrsim _C n^{3/2}$
by Lemma 7.3 and therefore
![]() $\lVert \vec {y}\rVert _2\gtrsim _C n^{3/2}$
.
$\lVert \vec {y}\rVert _2\gtrsim _C n^{3/2}$
.
Step 3: Rewriting X via bucket intersection sizes. Recall that we have a partition
![]() $V=I_1\cup \cdots \cup I_m$
into ‘buckets’ with
$V=I_1\cup \cdots \cup I_m$
into ‘buckets’ with
![]() $|I_1|=\cdots =|I_{m}|=|V|/m$
and
$|I_1|=\cdots =|I_{m}|=|V|/m$
and
![]() $|V|^{2\gamma }/2\leq m\leq 2|V|^{2\gamma }$
. Let
$|V|^{2\gamma }/2\leq m\leq 2|V|^{2\gamma }$
. Let
![]() $I\in \mathbb {R}^{V\times V}$
be the identity matrix, and let
$I\in \mathbb {R}^{V\times V}$
be the identity matrix, and let
![]() $Q\in \mathbb {R}^{V\times V}$
be the symmetric matrix defined by taking
$Q\in \mathbb {R}^{V\times V}$
be the symmetric matrix defined by taking
![]() $Q_{u,v}=1/|I_{k}|=m/|V|$
for
$Q_{u,v}=1/|I_{k}|=m/|V|$
for
![]() $u,v$
in the same bucket
$u,v$
in the same bucket
![]() $I_{k}$
, and
$I_{k}$
, and
![]() $Q_{u,v}=0$
otherwise. Multiplying a vector
$Q_{u,v}=0$
otherwise. Multiplying a vector
![]() $\vec {v}\in \mathbb {R}^V$
by this matrix Q has the effect of averaging the entries of
$\vec {v}\in \mathbb {R}^V$
by this matrix Q has the effect of averaging the entries of
![]() $\vec {v}$
over each of the buckets
$\vec {v}$
over each of the buckets
![]() $I_k$
, and hence
$I_k$
, and hence
![]() $(I-Q)\vec {v}$
has the property that for
$(I-Q)\vec {v}$
has the property that for
![]() $k=1,\ldots ,m$
the sum of the entries in
$k=1,\ldots ,m$
the sum of the entries in
![]() $\vec {v}_{I_k}$
is zero.
$\vec {v}_{I_k}$
is zero.
Let us define
![]() $\vec {\Delta }\in \mathbb {R}^V$
by
$\vec {\Delta }\in \mathbb {R}^V$
by
![]() $\vec {\Delta }=Q\vec {x}$
, so for any
$\vec {\Delta }=Q\vec {x}$
, so for any
![]() $k=1,\ldots ,m$
and any
$k=1,\ldots ,m$
and any
![]() $v\in I_k$
we have
$v\in I_k$
we have
 $$\begin{align*}\Delta_v=\frac{1}{|I_{k}|}\sum_{u\in I_{k}}x_{u}=\frac{2}{|I_{k}|}\left(|U\cap I_{k}|-\frac{|I_{k}|}{2}\right).\end{align*}$$
$$\begin{align*}\Delta_v=\frac{1}{|I_{k}|}\sum_{u\in I_{k}}x_{u}=\frac{2}{|I_{k}|}\left(|U\cap I_{k}|-\frac{|I_{k}|}{2}\right).\end{align*}$$
Hence,
![]() $\vec {\Delta }$
encodes the sizes of the intersections
$\vec {\Delta }$
encodes the sizes of the intersections
![]() $|U\cap I_{k}|$
for
$|U\cap I_{k}|$
for
![]() $k=1,\ldots ,m$
. In our analysis of the random variable X, we will condition on an outcome of
$k=1,\ldots ,m$
. In our analysis of the random variable X, we will condition on an outcome of
![]() $\vec {\Delta }$
and apply Lemma 11.1 to study X conditioned on
$\vec {\Delta }$
and apply Lemma 11.1 to study X conditioned on
![]() $\vec {\Delta }$
. However, the vector
$\vec {\Delta }$
. However, the vector
![]() $\vec {y}$
and the matrix M appearing in (12.2) do not satisfy conditions (a), (c) and (d) in Lemma 11.1. So, we need to modify the representation of X in (12.2).
$\vec {y}$
and the matrix M appearing in (12.2) do not satisfy conditions (a), (c) and (d) in Lemma 11.1. So, we need to modify the representation of X in (12.2).
Define
![]() $M^{*}=\frac {1}{8}(I-Q)M(I-Q)$
and
$M^{*}=\frac {1}{8}(I-Q)M(I-Q)$
and
![]() $\vec {w}^{*}_{\vec {\Delta }}=\frac {1}{2}(I-Q)(\vec {y}+\frac 12M\vec {\Delta })$
. Then (recalling that Q is symmetric)
$\vec {w}^{*}_{\vec {\Delta }}=\frac {1}{2}(I-Q)(\vec {y}+\frac 12M\vec {\Delta })$
. Then (recalling that Q is symmetric)
 $$ \begin{align} X&=E+\frac{1}{2}\vec{y}\cdot\vec{x}+\frac{1}{8}\vec{x}^{\intercal}M\vec{x}\notag\\ &=E+\frac{1}{2}(I-Q)\vec{y}\cdot\vec{x}+\frac{1}{2}\vec{y}\cdot (Q\vec{x})+\frac{1}{8}\vec{x}^{\intercal}(I-Q)M(I-Q)\vec{x}\notag\\ &\qquad\qquad+\frac{1}{4}\vec{x}^{\intercal}(I-Q)MQ\vec{x}+\frac{1}{8}\vec{x}^{\intercal}QMQ\vec{x}\notag\\ &=\left(E+\frac{1}{2}\vec{y}\cdot\vec{\Delta}+\frac{1}{8}\vec{\Delta}^{\intercal}M\vec{\Delta}\right)+\vec{w}^{*}_{\vec{\Delta}}\cdot\vec{x}+\vec{x}^{\intercal}M^{*}\vec{x}. \end{align} $$
$$ \begin{align} X&=E+\frac{1}{2}\vec{y}\cdot\vec{x}+\frac{1}{8}\vec{x}^{\intercal}M\vec{x}\notag\\ &=E+\frac{1}{2}(I-Q)\vec{y}\cdot\vec{x}+\frac{1}{2}\vec{y}\cdot (Q\vec{x})+\frac{1}{8}\vec{x}^{\intercal}(I-Q)M(I-Q)\vec{x}\notag\\ &\qquad\qquad+\frac{1}{4}\vec{x}^{\intercal}(I-Q)MQ\vec{x}+\frac{1}{8}\vec{x}^{\intercal}QMQ\vec{x}\notag\\ &=\left(E+\frac{1}{2}\vec{y}\cdot\vec{\Delta}+\frac{1}{8}\vec{\Delta}^{\intercal}M\vec{\Delta}\right)+\vec{w}^{*}_{\vec{\Delta}}\cdot\vec{x}+\vec{x}^{\intercal}M^{*}\vec{x}. \end{align} $$
Furthermore,
![]() $M^{*}$
has the property that for all
$M^{*}$
has the property that for all
![]() $k,h\in [m]$
, in the submatrix
$k,h\in [m]$
, in the submatrix
![]() $M^*[I_k\!\times \! I_h]$
all row and column sums are zero, and
$M^*[I_k\!\times \! I_h]$
all row and column sums are zero, and
![]() $\vec {w}^{*}_{\vec {\Delta }}$
has the property that for each
$\vec {w}^{*}_{\vec {\Delta }}$
has the property that for each
![]() $k=1,\ldots ,m$
, the sum of entries in
$k=1,\ldots ,m$
, the sum of entries in
![]() $(\vec {w}^{*}_{\vec {\Delta }})_{I_{k}}$
is equal to zero. Also, note that since M has entries in
$(\vec {w}^{*}_{\vec {\Delta }})_{I_{k}}$
is equal to zero. Also, note that since M has entries in
![]() $\{0,1\}$
, all entries of
$\{0,1\}$
, all entries of
![]() $(I-Q)MQ$
and hence all entries of
$(I-Q)MQ$
and hence all entries of
![]() $M^*$
have absolute value at most
$M^*$
have absolute value at most
![]() $1$
. Thus,
$1$
. Thus,
![]() $\vec {w}^{*}_{\vec {\Delta }}$
and
$\vec {w}^{*}_{\vec {\Delta }}$
and
![]() $M^*$
satisfy conditions (b)–(d) in Lemma 11.1.
$M^*$
satisfy conditions (b)–(d) in Lemma 11.1.
Also, since
![]() $M^{*}$
is defined in terms of the adjacency matrix of a Ramsey graph, Lemma 10.1 tells us that it must have large Frobenius norm. Indeed,
$M^{*}$
is defined in terms of the adjacency matrix of a Ramsey graph, Lemma 10.1 tells us that it must have large Frobenius norm. Indeed,
by Lemma 10.1 applied with
![]() $\delta =2\gamma =2\cdot 10^{-4}$
and
$\delta =2\gamma =2\cdot 10^{-4}$
and
![]() $r=3$
(here, we are using that M is the adjacency matrix of the
$r=3$
(here, we are using that M is the adjacency matrix of the
![]() $(2C)$
-Ramsey graph
$(2C)$
-Ramsey graph
![]() $G[V]$
of size
$G[V]$
of size
![]() $|V|\gtrsim n$
, and we are using that the matrix
$|V|\gtrsim n$
, and we are using that the matrix
![]() $B=MQ+QM-QMQ\in \mathbb {R}^{V\times V}$
has the property that
$B=MQ+QM-QMQ\in \mathbb {R}^{V\times V}$
has the property that
![]() $\operatorname {rank}B[I_{k}\!\times \! I_{h}]\leq 3$
for all
$\operatorname {rank}B[I_{k}\!\times \! I_{h}]\leq 3$
for all
![]() $k,h\in [m]$
).
$k,h\in [m]$
).
Step 4: Conditioning on bucket intersection sizes. By a Chernoff bound, with probability at least
![]() $1-2n^{2\gamma }\cdot n^{-\omega (1)}=1-n^{-\omega (1)}$
we have
$1-2n^{2\gamma }\cdot n^{-\omega (1)}=1-n^{-\omega (1)}$
we have
![]() $\big ||U\cap I_k|-|I_k|/2\big |\le \sqrt {|I_k|}(\log n)/2=\sqrt {|V|/m}\cdot (\log n)/2$
for
$\big ||U\cap I_k|-|I_k|/2\big |\le \sqrt {|I_k|}(\log n)/2=\sqrt {|V|/m}\cdot (\log n)/2$
for
![]() $k=1,\ldots ,m$
, or equivalently
$k=1,\ldots ,m$
, or equivalently
![]() $|\Delta _{v}|\le \sqrt {m/|V|}\log n$
for all
$|\Delta _{v}|\le \sqrt {m/|V|}\log n$
for all
![]() $v\in V$
.
$v\in V$
.
We furthermore claim that with probability
![]() $1-n^{-\omega (1)}$
we have
$1-n^{-\omega (1)}$
we have
![]() $\|\vec {w}^{*}_{\vec {\Delta }}\|_{\infty }\le n^{1/2+5\gamma }$
. Indeed, recall that
$\|\vec {w}^{*}_{\vec {\Delta }}\|_{\infty }\le n^{1/2+5\gamma }$
. Indeed, recall that
![]() $\vec {w}^{*}_{\vec {\Delta }}=\frac {1}{2}(I-Q)(\vec {y}+\frac 12M\vec {\Delta })$
and (from Step 2)
$\vec {w}^{*}_{\vec {\Delta }}=\frac {1}{2}(I-Q)(\vec {y}+\frac 12M\vec {\Delta })$
and (from Step 2)
![]() $|y_{v}-d_v|\le n^{1/2}$
for all
$|y_{v}-d_v|\le n^{1/2}$
for all
![]() $v\in V$
. Recall from the choice of buckets in Step 1 that for all
$v\in V$
. Recall from the choice of buckets in Step 1 that for all
![]() $k=1,\ldots ,m$
and
$k=1,\ldots ,m$
and
![]() $v\in I_k$
, we have
$v\in I_k$
, we have
![]() $|d_v-\kappa _k|\leq n^{1/2+4\gamma }$
, implying that
$|d_v-\kappa _k|\leq n^{1/2+4\gamma }$
, implying that
![]() $|y_{v}-\kappa _k|\le 2n^{1/2+4\gamma }$
. In particular, we obtain
$|y_{v}-\kappa _k|\le 2n^{1/2+4\gamma }$
. In particular, we obtain
![]() $|y_{v}-y_u|\le 4n^{1/2+4\gamma }$
for all
$|y_{v}-y_u|\le 4n^{1/2+4\gamma }$
for all
![]() $u,v\in V$
that are in the same bucket
$u,v\in V$
that are in the same bucket
![]() $I_k$
. Hence,
$I_k$
. Hence,
![]() $\lVert (I-Q)\vec {y}\rVert _{\infty }\leq 4n^{1/2+4\gamma }$
. Furthermore, since all entries of
$\lVert (I-Q)\vec {y}\rVert _{\infty }\leq 4n^{1/2+4\gamma }$
. Furthermore, since all entries of
![]() $(I-Q)MQ$
have absolute value at most
$(I-Q)MQ$
have absolute value at most
![]() $1$
, Theorem 4.15 (concentration via hypercontractivity) shows that with probability at least
$1$
, Theorem 4.15 (concentration via hypercontractivity) shows that with probability at least
![]() $1-n\cdot n^{-\omega (1)}=1-n^{-\omega (1)}$
we have
$1-n\cdot n^{-\omega (1)}=1-n^{-\omega (1)}$
we have
![]() $\|(I-Q)M\vec {\Delta }\|_{\infty }=\|(I-Q)MQ\vec x\|_{\infty }\le \sqrt {n}\log n$
, which now implies
$\|(I-Q)M\vec {\Delta }\|_{\infty }=\|(I-Q)MQ\vec x\|_{\infty }\le \sqrt {n}\log n$
, which now implies
![]() $\|\vec {w}^{*}_{\vec {\Delta }}\|_{\infty }\le n^{1/2+5\gamma }$
as claimed.
$\|\vec {w}^{*}_{\vec {\Delta }}\|_{\infty }\le n^{1/2+5\gamma }$
as claimed.
Let us say that an outcome of
![]() $\vec {\Delta }$
is near-balanced if
$\vec {\Delta }$
is near-balanced if
![]() $\|\vec {w}^{*}_{\vec {\Delta }}\|_{\infty }\le n^{1/2+5\gamma }$
and
$\|\vec {w}^{*}_{\vec {\Delta }}\|_{\infty }\le n^{1/2+5\gamma }$
and
![]() $|\Delta _{v}|\le \sqrt {m/|V|}\log n$
for all
$|\Delta _{v}|\le \sqrt {m/|V|}\log n$
for all
![]() $v\in V$
. We have just shown that
$v\in V$
. We have just shown that
![]() $\vec {\Delta }$
is near-balanced with probability
$\vec {\Delta }$
is near-balanced with probability
![]() $1-n^{-\omega (1)}$
. Note that for near-balanced
$1-n^{-\omega (1)}$
. Note that for near-balanced
![]() $\vec {\Delta }$
we in particular have
$\vec {\Delta }$
we in particular have
![]() $\|\vec {w}^{*}_{\vec {\Delta }}\|_{\infty }\le |V|^{1/2+6\gamma }$
and
$\|\vec {w}^{*}_{\vec {\Delta }}\|_{\infty }\le |V|^{1/2+6\gamma }$
and
![]() $\big ||U\cap I_k|-|I_k|/2\big |\le \sqrt {|V|/m}\cdot (\log n)/2\le \sqrt {|V|^{1-2\gamma }}\log |V|$
for
$\big ||U\cap I_k|-|I_k|/2\big |\le \sqrt {|V|/m}\cdot (\log n)/2\le \sqrt {|V|^{1-2\gamma }}\log |V|$
for
![]() $k=1,\ldots ,m$
. If we condition on a near-balanced outcome of
$k=1,\ldots ,m$
. If we condition on a near-balanced outcome of
![]() $\vec {\Delta }$
(which is equivalent to conditioning on the bucket intersection sizes
$\vec {\Delta }$
(which is equivalent to conditioning on the bucket intersection sizes
![]() $|U\cap I_k|$
for
$|U\cap I_k|$
for
![]() $k=1,\ldots ,m$
), then we are in a position to apply Lemma 11.1 with
$k=1,\ldots ,m$
), then we are in a position to apply Lemma 11.1 with
![]() $\delta =2\gamma =2\cdot 10^{-4}$
. Together with the machinery in Sections 6, 8, 10 and 5 we can then obtain upper and lower bounds for the probability that, conditioning on our outcome of
$\delta =2\gamma =2\cdot 10^{-4}$
. Together with the machinery in Sections 6, 8, 10 and 5 we can then obtain upper and lower bounds for the probability that, conditioning on our outcome of
![]() $\vec \Delta $
, the random variable X lies in some short interval.Footnote 10
$\vec \Delta $
, the random variable X lies in some short interval.Footnote 10
To state such upper and lower bounds, let us write
![]() $E_{\vec {\Delta }}=\mathbb E[X|\vec {\Delta }]$
and define
$E_{\vec {\Delta }}=\mathbb E[X|\vec {\Delta }]$
and define
![]() $\sigma _{\vec {\Delta }}\geq 0$
to satisfy
$\sigma _{\vec {\Delta }}\geq 0$
to satisfy
![]() $\sigma _{\vec {\Delta }}^{2}=\operatorname {Var}[X|\vec {\Delta }]$
. By Lemma 11.1(2), for near-balanced
$\sigma _{\vec {\Delta }}^{2}=\operatorname {Var}[X|\vec {\Delta }]$
. By Lemma 11.1(2), for near-balanced
![]() $\vec {\Delta }$
we have
$\vec {\Delta }$
we have
![]() $\sigma _{\vec {\Delta }}^{2}=2\|M^{*}\|_{\mathrm F}^{2}+\|\vec {w}^{*}_{\vec {\Delta }}\|_{2}^{2}+O(n^{7/4+14\gamma })$
, implying that
$\sigma _{\vec {\Delta }}^{2}=2\|M^{*}\|_{\mathrm F}^{2}+\|\vec {w}^{*}_{\vec {\Delta }}\|_{2}^{2}+O(n^{7/4+14\gamma })$
, implying that
![]() $\sigma _{\vec {\Delta }}\ge \|M^{*}\|_{\mathrm F}\gtrsim _C n$
by (12.4).
$\sigma _{\vec {\Delta }}\ge \|M^{*}\|_{\mathrm F}\gtrsim _C n$
by (12.4).
Claim 12.1. There is a constant
![]() $B=B(C)>0$
such that the following holds for any fixed near-balanced outcome of
$B=B(C)>0$
such that the following holds for any fixed near-balanced outcome of
![]() $\vec {\Delta }$
.
$\vec {\Delta }$
.
-
1. For any
 $x\in \mathbb Z$
, we have
$x\in \mathbb Z$
, we have  $$\begin{align*}\Pr\left[|X-x|\le B\middle|\vec{\Delta}\right]\lesssim_{C}\frac{\exp\left(-\Omega_{C}\left(|x-E_{\vec{\Delta}}|/\sigma_{\vec{\Delta}}\right)\right)+n^{-0.1}}{\sigma_{\vec{\Delta}}}. \end{align*}$$
$$\begin{align*}\Pr\left[|X-x|\le B\middle|\vec{\Delta}\right]\lesssim_{C}\frac{\exp\left(-\Omega_{C}\left(|x-E_{\vec{\Delta}}|/\sigma_{\vec{\Delta}}\right)\right)+n^{-0.1}}{\sigma_{\vec{\Delta}}}. \end{align*}$$
-
2. There is a sign
 $s\in \{-1,1\}$
, depending only on
$s\in \{-1,1\}$
, depending only on
 $M^*$
, such that for any fixed
$M^*$
, such that for any fixed
 $A>0$
and any
$A>0$
and any
 $x\in \mathbb Z$
satisfying
$x\in \mathbb Z$
satisfying
 $3n\le s(x-E_{\vec {\Delta }})\le A\sigma _{\vec {\Delta }}$
, we have
$3n\le s(x-E_{\vec {\Delta }})\le A\sigma _{\vec {\Delta }}$
, we have  $$\begin{align*}\Pr\left[|X-x|\le B\middle|\vec{\Delta}\right]\gtrsim_{C,A}\frac{1}{\sigma_{\vec{\Delta}}}. \end{align*}$$
$$\begin{align*}\Pr\left[|X-x|\le B\middle|\vec{\Delta}\right]\gtrsim_{C,A}\frac{1}{\sigma_{\vec{\Delta}}}. \end{align*}$$
We defer the proof of Claim 12.1 until the end of the section (specifically, we will prove it in Section 12.1). The proof combines the machinery from Sections 6, 8, 10, 5 and 11.
Step 5: Estimating the conditional mean and variance. We wish to average the estimates in Claim 12.1 over different near-balanced outcomes of
![]() $\vec {\Delta }$
. To this end, we need to understand how the conditional mean and variance
$\vec {\Delta }$
. To this end, we need to understand how the conditional mean and variance
![]() $E_{\vec {\Delta }}=\mathbb E[X|\vec {\Delta }]$
and
$E_{\vec {\Delta }}=\mathbb E[X|\vec {\Delta }]$
and
![]() $\sigma _{\vec {\Delta }}^{2}=\operatorname {Var}[X|\vec {\Delta }]$
depend on
$\sigma _{\vec {\Delta }}^{2}=\operatorname {Var}[X|\vec {\Delta }]$
depend on
![]() $\vec {\Delta }$
(recall that we already fixed an outcome for
$\vec {\Delta }$
(recall that we already fixed an outcome for
![]() $U\cap R$
in Step 2, which in particular fixes E and
$U\cap R$
in Step 2, which in particular fixes E and
![]() $\vec {y}$
). Most importantly,
$\vec {y}$
). Most importantly,
![]() $E_{\vec {\Delta }}$
positively correlates with the coordinates of
$E_{\vec {\Delta }}$
positively correlates with the coordinates of
![]() $\vec {\Delta }$
: Recall that
$\vec {\Delta }$
: Recall that
![]() $\vec {\Delta }$
encodes the number of vertices of our random set U in each bucket, so naturally if we take more vertices we are likely to increase the number of edges we end up with. However, there are also certain (lower order, nonlinear) adjustments that we need to take into account. In this subsection we will define ‘shift’ random variables
$\vec {\Delta }$
encodes the number of vertices of our random set U in each bucket, so naturally if we take more vertices we are likely to increase the number of edges we end up with. However, there are also certain (lower order, nonlinear) adjustments that we need to take into account. In this subsection we will define ‘shift’ random variables
![]() $E_{\mathrm {shift}(1)},E_{\mathrm {shift}(2)}$
and
$E_{\mathrm {shift}(1)},E_{\mathrm {shift}(2)}$
and
![]() $\sigma _{\mathrm {shift}}$
depending on
$\sigma _{\mathrm {shift}}$
depending on
![]() $\vec \Delta $
. We then show that these shift random variables control the dependence of
$\vec \Delta $
. We then show that these shift random variables control the dependence of
![]() $E_{\vec {\Delta }}$
and
$E_{\vec {\Delta }}$
and
![]() $\sigma _{\vec {\Delta }}$
on
$\sigma _{\vec {\Delta }}$
on
![]() $\vec \Delta $
.
$\vec \Delta $
.
Let
![]() $E_{\mathrm {shift}(1)}=\frac {1}{2}\vec {y}\cdot \vec {\Delta }$
and
$E_{\mathrm {shift}(1)}=\frac {1}{2}\vec {y}\cdot \vec {\Delta }$
and
![]() $E_{\mathrm {shift}(2)}=\frac {1}{8}\vec {\Delta }^{\intercal }M\vec {\Delta }$
. Recalling (12.3), by Lemma 11.1(1) (applied with
$E_{\mathrm {shift}(2)}=\frac {1}{8}\vec {\Delta }^{\intercal }M\vec {\Delta }$
. Recalling (12.3), by Lemma 11.1(1) (applied with
![]() $\delta =2\gamma $
) we have
$\delta =2\gamma $
) we have
![]() $E_{\vec {\Delta }}=\mathbb E[X|\vec {\Delta }]=E+E_{\mathrm {shift}(1)}+E_{\mathrm {shift}(2)}+\sum _{v\in V} M^*_{v,v}+O(n^{3/4+8\gamma })$
if
$E_{\vec {\Delta }}=\mathbb E[X|\vec {\Delta }]=E+E_{\mathrm {shift}(1)}+E_{\mathrm {shift}(2)}+\sum _{v\in V} M^*_{v,v}+O(n^{3/4+8\gamma })$
if
![]() $\vec {\Delta }$
is near-balanced. Recalling
$\vec {\Delta }$
is near-balanced. Recalling
![]() $\gamma =10^{-4}$
and that all entries of
$\gamma =10^{-4}$
and that all entries of
![]() $M^*$
have absolute value at most
$M^*$
have absolute value at most
![]() $1$
, we obtain
$1$
, we obtain
for all near-balanced
![]() $\vec {\Delta }$
(i.e.,
$\vec {\Delta }$
(i.e.,
![]() $E_{\vec {\Delta }}$
is ‘shifted’ by about
$E_{\vec {\Delta }}$
is ‘shifted’ by about
![]() $E_{\mathrm {shift}(1)}+E_{\mathrm {shift}(2)}$
from E).
$E_{\mathrm {shift}(1)}+E_{\mathrm {shift}(2)}$
from E).
Recall that
![]() $\|\vec y\|_2\gtrsim _C n^{3/2}$
and
$\|\vec y\|_2\gtrsim _C n^{3/2}$
and
![]() $\|\vec y\|_{\infty }\le (H+2)n$
from the end of Step 2. Furthermore, we observed that
$\|\vec y\|_{\infty }\le (H+2)n$
from the end of Step 2. Furthermore, we observed that
![]() $\|(I-Q)\vec y\|_{\infty }\le 4n^{1/2+4\gamma }$
in Step 4, which implies
$\|(I-Q)\vec y\|_{\infty }\le 4n^{1/2+4\gamma }$
in Step 4, which implies
![]() $\|(I-Q)\vec y\|_2\le 4n^{1+4\gamma }$
. Thus, we obtain
$\|(I-Q)\vec y\|_2\le 4n^{1+4\gamma }$
. Thus, we obtain
![]() $\|Q\vec y\|_2\ge \|\vec y\|_2-\|(I-Q)\vec y\|_2\gtrsim _C n^{3/2}$
and
$\|Q\vec y\|_2\ge \|\vec y\|_2-\|(I-Q)\vec y\|_2\gtrsim _C n^{3/2}$
and
![]() $\|Q\vec y\|_{\infty }\le (H+2)n$
. Roughly speaking, this means
$\|Q\vec y\|_{\infty }\le (H+2)n$
. Roughly speaking, this means
![]() $Q\vec y$
behaves like a vector where every entry has magnitude around n, and we can apply the Berry–Esseen theorem to
$Q\vec y$
behaves like a vector where every entry has magnitude around n, and we can apply the Berry–Esseen theorem to
![]() $E_{\mathrm {shift}(1)}=\frac 12\vec y\cdot \vec \Delta =\frac 12 (Q\vec y)\cdot \vec x=\sum _{v\in V}(\frac 12Q\vec y)_v x_v$
(the Berry–Esseen theorem is a quantitative central limit theorem for sums of independent but not necessarily identically distributed random variables; see, for example, [Reference Petrov and Brown83, Chapter V, Theorem 3]). Indeed, let
$E_{\mathrm {shift}(1)}=\frac 12\vec y\cdot \vec \Delta =\frac 12 (Q\vec y)\cdot \vec x=\sum _{v\in V}(\frac 12Q\vec y)_v x_v$
(the Berry–Esseen theorem is a quantitative central limit theorem for sums of independent but not necessarily identically distributed random variables; see, for example, [Reference Petrov and Brown83, Chapter V, Theorem 3]). Indeed, let
![]() $Z\sim \mathcal N(0,(\frac 12\|Q\vec y\|_2)^2)$
; the Berry–Esseen theorem shows that for any interval
$Z\sim \mathcal N(0,(\frac 12\|Q\vec y\|_2)^2)$
; the Berry–Esseen theorem shows that for any interval
![]() $[a,b]\subseteq \mathbb {R}$
, we have
$[a,b]\subseteq \mathbb {R}$
, we have
In particular, for every interval
![]() $[a,b]\subseteq \mathbb {R}$
of length
$[a,b]\subseteq \mathbb {R}$
of length
![]() $b-a\geq \|M^{*}\|_{\mathrm F}$
, we have
$b-a\geq \|M^{*}\|_{\mathrm F}$
, we have
(recalling that
![]() $\|M^{*}\|_{\mathrm F}\gtrsim _C n$
by (12.4)).
$\|M^{*}\|_{\mathrm F}\gtrsim _C n$
by (12.4)).
Recall from Step 4 that for near-balanced
![]() $\vec {\Delta }$
we have
$\vec {\Delta }$
we have
![]() $\sigma _{\vec {\Delta }}^{2}=2\|M^{*}\|_{\mathrm F}^{2}+\|\vec {w}^{*}_{\vec {\Delta }}\|_{2}^{2}+O(n^{7/4+14\gamma })= 2\|M^{*}\|_{\mathrm F}^{2}+\|\frac {1}{2}(I-Q)\vec {y}+\frac 14(I-Q)M\vec {\Delta }\|_{2}^{2}+O(n^{7/4+14\gamma })$
(using the definition of
$\sigma _{\vec {\Delta }}^{2}=2\|M^{*}\|_{\mathrm F}^{2}+\|\vec {w}^{*}_{\vec {\Delta }}\|_{2}^{2}+O(n^{7/4+14\gamma })= 2\|M^{*}\|_{\mathrm F}^{2}+\|\frac {1}{2}(I-Q)\vec {y}+\frac 14(I-Q)M\vec {\Delta }\|_{2}^{2}+O(n^{7/4+14\gamma })$
(using the definition of
![]() $\vec {w}^{*}_{\vec {\Delta }}$
in Step 3). Let us now define
$\vec {w}^{*}_{\vec {\Delta }}$
in Step 3). Let us now define
![]() $\sigma \geq 0$
to satisfy
$\sigma \geq 0$
to satisfy
![]() $\sigma ^2=2\|M^{*}\|_{\mathrm F}^{2}+\|\frac {1}{2}(I-Q)\vec {y}\|_{2}^{2}$
. Note that
$\sigma ^2=2\|M^{*}\|_{\mathrm F}^{2}+\|\frac {1}{2}(I-Q)\vec {y}\|_{2}^{2}$
. Note that
![]() $\sigma $
does not depend on
$\sigma $
does not depend on
![]() $\vec {\Delta }$
(in a moment we will define
$\vec {\Delta }$
(in a moment we will define
![]() $\sigma _{\mathrm {shift}}$
to bound the deviation of
$\sigma _{\mathrm {shift}}$
to bound the deviation of
![]() $\sigma _{\vec \Delta }$
from
$\sigma _{\vec \Delta }$
from
![]() $\sigma $
). Also, note that we have
$\sigma $
). Also, note that we have
![]() $\sigma \ge \|M^{*}\|_{\mathrm F}\gtrsim _C n$
(recalling (12.4)) and
$\sigma \ge \|M^{*}\|_{\mathrm F}\gtrsim _C n$
(recalling (12.4)) and
![]() $\sigma ^2\leq 2n^2+4n^{2+8\gamma }\le n^{2.1}$
, meaning that
$\sigma ^2\leq 2n^2+4n^{2+8\gamma }\le n^{2.1}$
, meaning that
![]() $\sigma \le n^{1.05}$
.
$\sigma \le n^{1.05}$
.
Finally, let us define
![]() $\sigma _{\mathrm {shift}}=\|\frac {1}{4}(I-Q)M\vec {\Delta }\|_{2}$
. Using the inequality
$\sigma _{\mathrm {shift}}=\|\frac {1}{4}(I-Q)M\vec {\Delta }\|_{2}$
. Using the inequality
![]() $\lVert \vec {v}+\vec {w}\rVert _2^2\le 2\lVert \vec {v}\rVert _2^2+2\lVert \vec {w}\rVert _2^2$
for any vectors
$\lVert \vec {v}+\vec {w}\rVert _2^2\le 2\lVert \vec {v}\rVert _2^2+2\lVert \vec {w}\rVert _2^2$
for any vectors
![]() $\vec {v},\vec {w}\in \mathbb {R}^V$
, as well as (12.4) (recalling that
$\vec {v},\vec {w}\in \mathbb {R}^V$
, as well as (12.4) (recalling that
![]() $\gamma =10^{-4}$
), for any near-balanced
$\gamma =10^{-4}$
), for any near-balanced
![]() $\vec {\Delta }$
we have
$\vec {\Delta }$
we have
Similarly (using
![]() $\lVert \vec {v}-\vec {w}\rVert _2^2\ge \frac 12\lVert \vec {v}\rVert _2^2-\lVert \vec {w}\rVert _2^2$
),
$\lVert \vec {v}-\vec {w}\rVert _2^2\ge \frac 12\lVert \vec {v}\rVert _2^2-\lVert \vec {w}\rVert _2^2$
),
Therefore, for every near-balanced
![]() $\vec {\Delta }$
, we must have
$\vec {\Delta }$
, we must have
![]() $\sigma _{\vec {\Delta }}\le 2\sigma _{\mathrm {shift}}$
or
$\sigma _{\vec {\Delta }}\le 2\sigma _{\mathrm {shift}}$
or
![]() $\sigma /2\le \sigma _{\vec {\Delta }}\le 2\sigma $
(indeed, if
$\sigma /2\le \sigma _{\vec {\Delta }}\le 2\sigma $
(indeed, if
![]() $\sigma _{\mathrm {shift}}^2\leq \sigma _{\vec {\Delta }}^2/4$
, then
$\sigma _{\mathrm {shift}}^2\leq \sigma _{\vec {\Delta }}^2/4$
, then
![]() $\sigma _{\vec {\Delta }}^{2}/2\leq 2\sigma ^2$
and
$\sigma _{\vec {\Delta }}^{2}/2\leq 2\sigma ^2$
and
![]() $(5/4)\sigma _{\vec {\Delta }}^{2}\geq \sigma ^2/2$
).
$(5/4)\sigma _{\vec {\Delta }}^{2}\geq \sigma ^2/2$
).
Step 6: Controlling correlations of the shifts. In order to average the estimates in Claim 12.1 over the different outcomes of
![]() $\vec {\Delta }$
, we need to ensure that the ‘shifts’
$\vec {\Delta }$
, we need to ensure that the ‘shifts’
![]() $\sigma _{\mathrm {shift}},E_{\mathrm {shift}(1)},E_{\mathrm {shift}(2)}$
(each of which are determined by
$\sigma _{\mathrm {shift}},E_{\mathrm {shift}(1)},E_{\mathrm {shift}(2)}$
(each of which are determined by
![]() $\vec {\Delta }$
) do not correlate adversarially with each other. More specifically, we need that the quantities
$\vec {\Delta }$
) do not correlate adversarially with each other. More specifically, we need that the quantities
![]() $\sigma _{\mathrm {shift}},E_{\mathrm {shift}(2)}$
do not correlate very strongly with
$\sigma _{\mathrm {shift}},E_{\mathrm {shift}(2)}$
do not correlate very strongly with
![]() $E_{\mathrm {shift}(1)}$
, as shown in the following claim.
$E_{\mathrm {shift}(1)}$
, as shown in the following claim.
Claim 12.2. Let
![]() $[a,b]\subseteq \mathbb {R}$
be an interval of length
$[a,b]\subseteq \mathbb {R}$
be an interval of length
![]() $b-a\ge \|M^{*}\|_{\mathrm F}$
. Then
$b-a\ge \|M^{*}\|_{\mathrm F}$
. Then
In order to prove Claim 12.2, we will use a similar Fourier-analytic argument as in the proof of Lemma 6.1 to estimate expressions of the form
![]() , and deduce the desired bounds by linearity of expectation. We defer the details of this proof to the end of the section (specifically, we will prove it in Section 12.1).
, and deduce the desired bounds by linearity of expectation. We defer the details of this proof to the end of the section (specifically, we will prove it in Section 12.1).
After all this setup, we are now ready to prove the desired bounds in the statement of Theorem 3.1. Let
![]() $B=B(C)>0$
be as in Claim 12.1. Consider
$B=B(C)>0$
be as in Claim 12.1. Consider
![]() $x\in \mathbb {Z}$
, and write
$x\in \mathbb {Z}$
, and write
![]() $x'=x-E$
. Let
$x'=x-E$
. Let
![]() $\mathcal {E}$
be the event that
$\mathcal {E}$
be the event that
![]() $|X-x|\le B$
. We wish to prove the upper bound
$|X-x|\le B$
. We wish to prove the upper bound
![]() $\Pr [\mathcal {E}]\lesssim _{C,H} n^{-3/2}$
, and if
$\Pr [\mathcal {E}]\lesssim _{C,H} n^{-3/2}$
, and if
![]() $|x'|\le (A+1)n^{3/2}$
for some fixed
$|x'|\le (A+1)n^{3/2}$
for some fixed
![]() $A>0$
we wish to prove the lower bound
$A>0$
we wish to prove the lower bound
![]() $\Pr [\mathcal {E}]\gtrsim _{C, H, A}n^{-3/2}$
(recall that
$\Pr [\mathcal {E}]\gtrsim _{C, H, A}n^{-3/2}$
(recall that
![]() $|E-\mathbb E X|\le n^{3/2}$
from Step 2, so we have
$|E-\mathbb E X|\le n^{3/2}$
from Step 2, so we have
![]() $|x'|=|x-E|\le (A+1)n^{3/2}$
whenever
$|x'|=|x-E|\le (A+1)n^{3/2}$
whenever
![]() $|x-\mathbb {E}X|\le An^{3/2}$
).
$|x-\mathbb {E}X|\le An^{3/2}$
).
Step 7: Proof of the upper bound. First, recall from Step 4 that
![]() $\vec \Delta $
is near-balanced with probability
$\vec \Delta $
is near-balanced with probability
![]() $1-n^{-\omega (1)}$
. Also, for
$1-n^{-\omega (1)}$
. Also, for
![]() $\mathcal {E}$
to have an appreciable chance of occurring,
$\mathcal {E}$
to have an appreciable chance of occurring,
![]() $E_{\mathrm {shift}(1)}$
must be quite close to
$E_{\mathrm {shift}(1)}$
must be quite close to
![]() $x'$
. Indeed, note that if
$x'$
. Indeed, note that if
![]() $\mathcal {E}$
occurs,
$\mathcal {E}$
occurs,
![]() $\vec {\Delta }$
is near-balanced, and
$\vec {\Delta }$
is near-balanced, and
![]() $|E_{\mathrm {shift}(1)}-x'|\ge \sigma (\log n)^2$
, then we have
$|E_{\mathrm {shift}(1)}-x'|\ge \sigma (\log n)^2$
, then we have
(recalling that
![]() $\sigma \geq \lVert M^*\rVert _{\mathrm F}\gtrsim _C n$
from Step 5). On the other hand, by (12.2) we have (recalling that
$\sigma \geq \lVert M^*\rVert _{\mathrm F}\gtrsim _C n$
from Step 5). On the other hand, by (12.2) we have (recalling that
![]() $E_{\mathrm {shift}(1)}=\frac {1}{2}\vec {y}\cdot \vec {\Delta }=\frac {1}{2}(Q\vec {y})\cdot \vec {x}$
)
$E_{\mathrm {shift}(1)}=\frac {1}{2}\vec {y}\cdot \vec {\Delta }=\frac {1}{2}(Q\vec {y})\cdot \vec {x}$
)
Hence (as M is a symmetric matrix with zeroes on the diagonal), we have
![]() $\mathbb {E}[X-E-E_{\mathrm {shift}(1)}]=0$
and
$\mathbb {E}[X-E-E_{\mathrm {shift}(1)}]=0$
and
![]() $\sigma (X-E-E_{\mathrm {shift}(1)})^2=\frac {1}{32}\|M\|_{\mathrm F}^{2}+\|\frac {1}{2}(I-Q)\vec {y}\|_{2}^{2}\le n^2+\sigma ^2\lesssim _C \sigma ^2$
by (4.5) and the definition of
$\sigma (X-E-E_{\mathrm {shift}(1)})^2=\frac {1}{32}\|M\|_{\mathrm F}^{2}+\|\frac {1}{2}(I-Q)\vec {y}\|_{2}^{2}\le n^2+\sigma ^2\lesssim _C \sigma ^2$
by (4.5) and the definition of
![]() $\sigma $
in Step 5. Thus, accounting for the probability that
$\sigma $
in Step 5. Thus, accounting for the probability that
![]() $\vec \Delta $
is not near-balanced, we have
$\vec \Delta $
is not near-balanced, we have
 $$ \begin{align} \Pr[\mathcal E\cap \{|E_{\mathrm{shift}(1)}-x'|\ge \sigma(\log n)^2\}]&\le \Pr[|X-E-E_{\mathrm{shift}(1)}|\geq \sigma(\log n)^2/2]+n^{-\omega(1)}\notag \\ &\leq n^{-\omega_C(1)}\le n^{-3/2} \end{align} $$
$$ \begin{align} \Pr[\mathcal E\cap \{|E_{\mathrm{shift}(1)}-x'|\ge \sigma(\log n)^2\}]&\le \Pr[|X-E-E_{\mathrm{shift}(1)}|\geq \sigma(\log n)^2/2]+n^{-\omega(1)}\notag \\ &\leq n^{-\omega_C(1)}\le n^{-3/2} \end{align} $$
by Theorem 4.15 (concentration via hypercontractivity).
So, it suffices to restrict our attention to
![]() $\vec \Delta $
which are near-balanced and satisfy
$\vec \Delta $
which are near-balanced and satisfy
![]() $|E_{\mathrm {shift}(1)}-x'|\le \sigma (\log n)^2$
. The plan is to apply Claim 12.1(1) to upper-bound
$|E_{\mathrm {shift}(1)}-x'|\le \sigma (\log n)^2$
. The plan is to apply Claim 12.1(1) to upper-bound
![]() $\Pr [\mathcal E|\vec \Delta ]$
for all such
$\Pr [\mathcal E|\vec \Delta ]$
for all such
![]() $\vec \Delta $
, and then to average over
$\vec \Delta $
, and then to average over
![]() $\vec \Delta $
. When we apply Claim 12.1(1), we need estimates on
$\vec \Delta $
. When we apply Claim 12.1(1), we need estimates on
![]() $\sigma _{\vec \Delta }$
and
$\sigma _{\vec \Delta }$
and
![]() $|x-E_{\vec \Delta }|$
; we obtain these estimates in different ways depending on properties of
$|x-E_{\vec \Delta }|$
; we obtain these estimates in different ways depending on properties of
![]() $E_{\mathrm {shift}(1)},E_{\mathrm {shift}(2)},\sigma _{\mathrm {shift}}$
.
$E_{\mathrm {shift}(1)},E_{\mathrm {shift}(2)},\sigma _{\mathrm {shift}}$
.
First, the exponential decay in the bound in Claim 12.1(1) is in terms of
![]() $|x-E_{\vec \Delta }|$
. From (12.5), one can deduce that
$|x-E_{\vec \Delta }|$
. From (12.5), one can deduce that
![]() $|x-E_{\vec \Delta }|$
is at least roughly as large as
$|x-E_{\vec \Delta }|$
is at least roughly as large as
![]() $|x'-E_{\mathrm {shift}(1)}|$
, unless
$|x'-E_{\mathrm {shift}(1)}|$
, unless
![]() $E_{\mathrm {shift}(2)}$
is atypically large (at the end of this step we will upper-bound the contribution from such atypical
$E_{\mathrm {shift}(2)}$
is atypically large (at the end of this step we will upper-bound the contribution from such atypical
![]() $\vec \Delta $
). Let
$\vec \Delta $
). Let
![]() $\mathcal {H}$
be the event that
$\mathcal {H}$
be the event that
![]() $\vec \Delta $
is near-balanced and satisfies
$\vec \Delta $
is near-balanced and satisfies
![]() $|E_{\mathrm {shift}(1)}-x'|\le \sigma (\log n)^2$
and
$|E_{\mathrm {shift}(1)}-x'|\le \sigma (\log n)^2$
and
![]() $|x-E_{\vec {\Delta }}|\geq |E_{\mathrm {shift}(1)}-x'|/2-2n$
; we start by upper-bounding
$|x-E_{\vec {\Delta }}|\geq |E_{\mathrm {shift}(1)}-x'|/2-2n$
; we start by upper-bounding
![]() $\Pr [\mathcal E\cap \mathcal H]$
.
$\Pr [\mathcal E\cap \mathcal H]$
.
For any outcome of
![]() $\vec {\Delta }$
such that
$\vec {\Delta }$
such that
![]() $\mathcal {H}$
holds, by Claim 12.1(1) we have
$\mathcal {H}$
holds, by Claim 12.1(1) we have
 $$ \begin{align} \Pr\left[|X-x|\le B\middle|\vec{\Delta}\right]&\lesssim_C \frac{\exp\left(-\Omega_{C}\left(|x-E_{\vec{\Delta}}|/\sigma_{\vec{\Delta}}\right)\right)+n^{-0.1}}{\sigma_{\vec{\Delta}}}\notag\\ &\lesssim_{C}\frac{\exp\left(-\Omega_{C}\left(|E_{\mathrm{shift}(1)}-x'|/\sigma_{\vec{\Delta}}\right)\right)}{\sigma_{\vec{\Delta}}}+n^{-1.1} \end{align} $$
$$ \begin{align} \Pr\left[|X-x|\le B\middle|\vec{\Delta}\right]&\lesssim_C \frac{\exp\left(-\Omega_{C}\left(|x-E_{\vec{\Delta}}|/\sigma_{\vec{\Delta}}\right)\right)+n^{-0.1}}{\sigma_{\vec{\Delta}}}\notag\\ &\lesssim_{C}\frac{\exp\left(-\Omega_{C}\left(|E_{\mathrm{shift}(1)}-x'|/\sigma_{\vec{\Delta}}\right)\right)}{\sigma_{\vec{\Delta}}}+n^{-1.1} \end{align} $$
(recalling from Step 4 that
![]() $\sigma _{\vec {\Delta }}\ge \|M^{*}\|_{\mathrm F}\gtrsim _C n$
). Also, note that by (12.7), we have
$\sigma _{\vec {\Delta }}\ge \|M^{*}\|_{\mathrm F}\gtrsim _C n$
). Also, note that by (12.7), we have
(recalling that
![]() $\sigma \ge \|M^{*}\|_{\mathrm F}$
and
$\sigma \ge \|M^{*}\|_{\mathrm F}$
and
![]() $\sigma \le n^{1.05}$
from Step 5).
$\sigma \le n^{1.05}$
from Step 5).
Recall from the end of Step 5 that we always have
![]() $\sigma _{\vec {\Delta }}\le 2\sigma _{\mathrm {shift}}$
or
$\sigma _{\vec {\Delta }}\le 2\sigma _{\mathrm {shift}}$
or
![]() $\sigma /2\le \sigma _{\vec {\Delta }}\le 2\sigma $
. First, we bound
$\sigma /2\le \sigma _{\vec {\Delta }}\le 2\sigma $
. First, we bound
 $$ \begin{align*} &\Pr[\mathcal{E}\cap \mathcal{H}\cap \{\sigma/2\le \sigma_{\vec{\Delta}}\le 2\sigma\}] \\ & = \sum_{j=0}^{\infty} \Pr\bigg[\mathcal{E}\cap\mathcal{H}\cap\{\sigma/2\le \sigma_{\vec{\Delta}}\le 2\sigma\}\cap\bigg\{j\le \frac{|E_{\mathrm{shift}(1)}-x'|}{\sigma}<j+1\bigg\}\bigg] \\ & \lesssim_C \sum_{j=0}^{\infty} \Pr\bigg[\mathcal{H}\cap (\sigma/2\le \sigma_{\vec{\Delta}}\le 2\sigma)\cap \bigg\{j\le \frac{|E_{\mathrm{shift}(1)}-x'|}{\sigma}<j+1\bigg\}\bigg] \bigg(\frac{\exp\left(-\Omega_{C}(j)\right)}{\sigma}+n^{-1.1}\bigg) \\ & \le \Pr[\mathcal{H}]\cdot n^{-1.1}+\sum_{j=0}^{\infty} \Pr\bigg[j\le \frac{|E_{\mathrm{shift}(1)}-x'|}{\sigma}<j+1\bigg] \cdot \frac{\exp\left(-\Omega_{C}(j)\right)}{\sigma}\\ & \lesssim_{C,H} n^{-0.45}(\log n)^2\cdot n^{-1.1}+\sum_{j=0}^{\infty} \frac{\sigma}{n^{3/2}}\cdot \frac{\exp\left(-\Omega_{C}(j)\right)}{\sigma}\lesssim_C n^{-3/2}, \end{align*} $$
$$ \begin{align*} &\Pr[\mathcal{E}\cap \mathcal{H}\cap \{\sigma/2\le \sigma_{\vec{\Delta}}\le 2\sigma\}] \\ & = \sum_{j=0}^{\infty} \Pr\bigg[\mathcal{E}\cap\mathcal{H}\cap\{\sigma/2\le \sigma_{\vec{\Delta}}\le 2\sigma\}\cap\bigg\{j\le \frac{|E_{\mathrm{shift}(1)}-x'|}{\sigma}<j+1\bigg\}\bigg] \\ & \lesssim_C \sum_{j=0}^{\infty} \Pr\bigg[\mathcal{H}\cap (\sigma/2\le \sigma_{\vec{\Delta}}\le 2\sigma)\cap \bigg\{j\le \frac{|E_{\mathrm{shift}(1)}-x'|}{\sigma}<j+1\bigg\}\bigg] \bigg(\frac{\exp\left(-\Omega_{C}(j)\right)}{\sigma}+n^{-1.1}\bigg) \\ & \le \Pr[\mathcal{H}]\cdot n^{-1.1}+\sum_{j=0}^{\infty} \Pr\bigg[j\le \frac{|E_{\mathrm{shift}(1)}-x'|}{\sigma}<j+1\bigg] \cdot \frac{\exp\left(-\Omega_{C}(j)\right)}{\sigma}\\ & \lesssim_{C,H} n^{-0.45}(\log n)^2\cdot n^{-1.1}+\sum_{j=0}^{\infty} \frac{\sigma}{n^{3/2}}\cdot \frac{\exp\left(-\Omega_{C}(j)\right)}{\sigma}\lesssim_C n^{-3/2}, \end{align*} $$
where in the first inequality we used (12.9) and in the final inequality we used (12.7) (recalling that
![]() $\sigma \geq \|M^{*}\|_{\mathrm F}$
).
$\sigma \geq \|M^{*}\|_{\mathrm F}$
).
Next, let us bound
![]() $\Pr [\mathcal {E}\cap \mathcal {H}\cap \{\sigma _{\vec {\Delta }}\le 2\sigma _{\mathrm {shift}}\}]$
. Note that Claim 12.2 implies
$\Pr [\mathcal {E}\cap \mathcal {H}\cap \{\sigma _{\vec {\Delta }}\le 2\sigma _{\mathrm {shift}}\}]$
. Note that Claim 12.2 implies
for any interval
![]() $[a,b]\subseteq \mathbb {R}$
of length
$[a,b]\subseteq \mathbb {R}$
of length
![]() $b-a\ge \|M^{*}\|_{\mathrm F}$
. Hence, recalling from Step 4 that
$b-a\ge \|M^{*}\|_{\mathrm F}$
. Hence, recalling from Step 4 that
![]() $\sigma _{\vec {\Delta }}\ge \|M^{*}\|_{\mathrm F}\gtrsim _C n$
for every near-balanced
$\sigma _{\vec {\Delta }}\ge \|M^{*}\|_{\mathrm F}\gtrsim _C n$
for every near-balanced
![]() $\vec {\Delta }$
, we obtain
$\vec {\Delta }$
, we obtain
 $$ \begin{align*} &\Pr[\mathcal{E}\cap \mathcal{H}\cap \{\sigma_{\vec{\Delta}}\le 2\sigma_{\mathrm{shift}}\}] \\ &= \sum_{i,j=0}^{\infty} \Pr\!\bigg[\mathcal{E}\cap \mathcal{H}\cap \{\sigma_{\vec{\Delta}}\le 2\sigma_{\mathrm{shift}}\}\cap \bigg\{2^i\le \frac{\sigma_{\vec{\Delta}}}{\|M^{*}\|_{\mathrm F}}< 2^{i+1}\bigg\}\cap \bigg\{j\le \frac{|E_{\mathrm{shift}(1)}-x'|}{2^i\|M^{*}\|_{\mathrm F}}<j+1\bigg\}\bigg] \\ &\lesssim_C \sum_{i,j=0}^{\infty} \Pr\bigg[\mathcal{H}\cap \{\sigma_{\vec{\Delta}}\le 2\sigma_{\mathrm{shift}}\}\cap\bigg\{2^i\le \frac{\sigma_{\vec{\Delta}}}{\|M^{*}\|_{\mathrm F}}< 2^{i+1}\bigg\}\cap \bigg\{j\le \frac{|E_{\mathrm{shift}(1)}-x'|}{2^i\|M^{*}\|_{\mathrm F}}<j+1\bigg\}\bigg] \\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\cdot \left(\frac{\exp\left(-\Omega_{C}(j)\right)}{2^i\|M^{*}\|_{\mathrm F}}+n^{-1.1}\right)\\ &\le \frac{\Pr[\mathcal{H}]}{n^{1.1}}+\sum_{i,j=0}^{\infty} \Pr\bigg[\{\sigma_{\vec{\Delta}}\le 2\sigma_{\mathrm{shift}}\}\cap \bigg\{2^i\le \frac{\sigma_{\vec{\Delta}}}{\|M^{*}\|_{\mathrm F}}\bigg\}\cap \bigg\{j\le \frac{|E_{\mathrm{shift}(1)}-x'|}{2^i\|M^{*}\|_{\mathrm F}}<j+1\bigg\}\bigg]\\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\cdot \frac{\exp\left(-\Omega_{C}(j)\right)}{2^i\|M^{*}\|_{\mathrm F}}\\ &\lesssim_{C,H} n^{-0.45}(\log n)^2\cdot n^{-1.1}+\sum_{i,j=0}^{\infty} \frac{n^{1/2}2^i\|M^{*}\|_{\mathrm F}}{(2^i\|M^{*}\|_{\mathrm F})^2}\cdot \frac{\exp\left(-\Omega_{C}(j)\right)}{2^i\|M^{*}\|_{\mathrm F}}\\ &=n^{-1.55}(\log n)^2+\sum_{i,j=0}^{\infty} \frac{n^{1/2}}{2^{2i}\|M^{*}\|_{\mathrm F}^2}\cdot \exp\left(-\Omega_{C}(j)\right)\lesssim_C n^{-3/2}+\frac{n^{1/2}}{\|M^{*}\|_{\mathrm F}^2}\lesssim_C n^{-3/2}. \end{align*} $$
$$ \begin{align*} &\Pr[\mathcal{E}\cap \mathcal{H}\cap \{\sigma_{\vec{\Delta}}\le 2\sigma_{\mathrm{shift}}\}] \\ &= \sum_{i,j=0}^{\infty} \Pr\!\bigg[\mathcal{E}\cap \mathcal{H}\cap \{\sigma_{\vec{\Delta}}\le 2\sigma_{\mathrm{shift}}\}\cap \bigg\{2^i\le \frac{\sigma_{\vec{\Delta}}}{\|M^{*}\|_{\mathrm F}}< 2^{i+1}\bigg\}\cap \bigg\{j\le \frac{|E_{\mathrm{shift}(1)}-x'|}{2^i\|M^{*}\|_{\mathrm F}}<j+1\bigg\}\bigg] \\ &\lesssim_C \sum_{i,j=0}^{\infty} \Pr\bigg[\mathcal{H}\cap \{\sigma_{\vec{\Delta}}\le 2\sigma_{\mathrm{shift}}\}\cap\bigg\{2^i\le \frac{\sigma_{\vec{\Delta}}}{\|M^{*}\|_{\mathrm F}}< 2^{i+1}\bigg\}\cap \bigg\{j\le \frac{|E_{\mathrm{shift}(1)}-x'|}{2^i\|M^{*}\|_{\mathrm F}}<j+1\bigg\}\bigg] \\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\cdot \left(\frac{\exp\left(-\Omega_{C}(j)\right)}{2^i\|M^{*}\|_{\mathrm F}}+n^{-1.1}\right)\\ &\le \frac{\Pr[\mathcal{H}]}{n^{1.1}}+\sum_{i,j=0}^{\infty} \Pr\bigg[\{\sigma_{\vec{\Delta}}\le 2\sigma_{\mathrm{shift}}\}\cap \bigg\{2^i\le \frac{\sigma_{\vec{\Delta}}}{\|M^{*}\|_{\mathrm F}}\bigg\}\cap \bigg\{j\le \frac{|E_{\mathrm{shift}(1)}-x'|}{2^i\|M^{*}\|_{\mathrm F}}<j+1\bigg\}\bigg]\\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\cdot \frac{\exp\left(-\Omega_{C}(j)\right)}{2^i\|M^{*}\|_{\mathrm F}}\\ &\lesssim_{C,H} n^{-0.45}(\log n)^2\cdot n^{-1.1}+\sum_{i,j=0}^{\infty} \frac{n^{1/2}2^i\|M^{*}\|_{\mathrm F}}{(2^i\|M^{*}\|_{\mathrm F})^2}\cdot \frac{\exp\left(-\Omega_{C}(j)\right)}{2^i\|M^{*}\|_{\mathrm F}}\\ &=n^{-1.55}(\log n)^2+\sum_{i,j=0}^{\infty} \frac{n^{1/2}}{2^{2i}\|M^{*}\|_{\mathrm F}^2}\cdot \exp\left(-\Omega_{C}(j)\right)\lesssim_C n^{-3/2}+\frac{n^{1/2}}{\|M^{*}\|_{\mathrm F}^2}\lesssim_C n^{-3/2}. \end{align*} $$
(The first inequality is by (12.9) and in the third inequality we used (12.10) with Markov’s inequality.)
We have now proved that
![]() $\Pr [\mathcal {E}\cap \mathcal {H}]\lesssim _{C,H} n^{-3/2}$
. Recalling the definition of
$\Pr [\mathcal {E}\cap \mathcal {H}]\lesssim _{C,H} n^{-3/2}$
. Recalling the definition of
![]() $\mathcal H$
and (12.8), it now suffices to upper-bound the probability that
$\mathcal H$
and (12.8), it now suffices to upper-bound the probability that
![]() $\mathcal E$
holds,
$\mathcal E$
holds,
![]() $\vec \Delta $
is near-balanced and
$\vec \Delta $
is near-balanced and
![]() $|x-E_{\vec {\Delta }}|\leq |E_{\mathrm {shift}(1)}-x'|/2-2n$
.
$|x-E_{\vec {\Delta }}|\leq |E_{\mathrm {shift}(1)}-x'|/2-2n$
.
If
![]() $\vec {\Delta }$
is near-balanced and
$\vec {\Delta }$
is near-balanced and
![]() $|x-E_{\vec {\Delta }}|\leq |E_{\mathrm {shift}(1)}-x'|/2-2n$
, then
$|x-E_{\vec {\Delta }}|\leq |E_{\mathrm {shift}(1)}-x'|/2-2n$
, then
![]() $|E_{\mathrm {shift}(1)}-x'|\geq 4n$
and, using
$|E_{\mathrm {shift}(1)}-x'|\geq 4n$
and, using
![]() $x'=x-E$
and (12.5), furthermore
$x'=x-E$
and (12.5), furthermore
![]() $|E_{\mathrm {shift}(2)}|\geq |E_{\mathrm {shift}(1)}+E-x|-|E_{\vec {\Delta }}-x|-2n\geq |E_{\mathrm {shift}(1)}-x'|/2$
. Hence (using Claim 12.2 noting that
$|E_{\mathrm {shift}(2)}|\geq |E_{\mathrm {shift}(1)}+E-x|-|E_{\vec {\Delta }}-x|-2n\geq |E_{\mathrm {shift}(1)}-x'|/2$
. Hence (using Claim 12.2 noting that
![]() $\lVert M^*\rVert _{\mathrm F}\le n$
and Markov’s inequality),
$\lVert M^*\rVert _{\mathrm F}\le n$
and Markov’s inequality),
 $$ \begin{align*} &\Pr[|x-E_{\vec{\Delta}}|\leq |E_{\mathrm{shift}(1)}-x'|/2-2n \text{ and }\vec{\Delta}\text{ is near-balanced}]\\ &\leq \sum_{i=2}^{\infty}\Pr[(2^i n\le |E_{\mathrm{shift}(1)}-x'|<2^{i+1} n)\cap (|E_{\mathrm{shift}(2)}|\geq 2^{i-1}n)]\lesssim_{C,H} \sum_{i=2}^{\infty}\frac{n^{1/2}\cdot 2^i n}{2^{2(i-1)}n^2}\lesssim n^{-1/2}. \end{align*} $$
$$ \begin{align*} &\Pr[|x-E_{\vec{\Delta}}|\leq |E_{\mathrm{shift}(1)}-x'|/2-2n \text{ and }\vec{\Delta}\text{ is near-balanced}]\\ &\leq \sum_{i=2}^{\infty}\Pr[(2^i n\le |E_{\mathrm{shift}(1)}-x'|<2^{i+1} n)\cap (|E_{\mathrm{shift}(2)}|\geq 2^{i-1}n)]\lesssim_{C,H} \sum_{i=2}^{\infty}\frac{n^{1/2}\cdot 2^i n}{2^{2(i-1)}n^2}\lesssim n^{-1/2}. \end{align*} $$
For every near-balanced outcome of
![]() $\vec {\Delta }$
, by Claim 12.1(1) we have
$\vec {\Delta }$
, by Claim 12.1(1) we have
![]() $\Pr [\mathcal {E}|\vec {\Delta }]\lesssim _C 1/\sigma _{\vec {\Delta }}\lesssim _C 1/n$
(recalling from Step 4 that
$\Pr [\mathcal {E}|\vec {\Delta }]\lesssim _C 1/\sigma _{\vec {\Delta }}\lesssim _C 1/n$
(recalling from Step 4 that
![]() $\sigma _{\vec {\Delta }}\ge \|M^{*}\|_{\mathrm F}\gtrsim _C n$
). Hence the probability that
$\sigma _{\vec {\Delta }}\ge \|M^{*}\|_{\mathrm F}\gtrsim _C n$
). Hence the probability that
![]() $\mathcal {E}$
holds,
$\mathcal {E}$
holds,
![]() $\vec {\Delta }$
is near-balanced, and
$\vec {\Delta }$
is near-balanced, and
![]() $|x-E_{\vec {\Delta }}|\leq |E_{\mathrm {shift}(1)}-x'|/2-2n$
is bounded by
$|x-E_{\vec {\Delta }}|\leq |E_{\mathrm {shift}(1)}-x'|/2-2n$
is bounded by
![]() $O_{C,H}(n^{-3/2})$
, completing the proof of the upper bound.
$O_{C,H}(n^{-3/2})$
, completing the proof of the upper bound.
Step 8: Proof of the lower bound. Fix
![]() $A>0$
, and assume that
$A>0$
, and assume that
![]() $|x-E|=|x'|\le (A+1)n^{3/2}$
. We need to show that
$|x-E|=|x'|\le (A+1)n^{3/2}$
. We need to show that
![]() $\Pr [\mathcal {E}]\gtrsim _{C,H,A} n^{-3/2}$
. To do so, we define an event
$\Pr [\mathcal {E}]\gtrsim _{C,H,A} n^{-3/2}$
. To do so, we define an event
![]() $\mathcal {F}$
such that we can conveniently apply Claim 12.1(2) after conditioning on this event (roughly speaking, we need
$\mathcal {F}$
such that we can conveniently apply Claim 12.1(2) after conditioning on this event (roughly speaking, we need
![]() $E_{\mathrm {shift}(1)}$
to take ‘about the right value’, and we need
$E_{\mathrm {shift}(1)}$
to take ‘about the right value’, and we need
![]() $E_{\mathrm {shift}(2)}$
and
$E_{\mathrm {shift}(2)}$
and
![]() $\sigma _{\mathrm {shift}}$
‘not to be too large’). We study the probability of
$\sigma _{\mathrm {shift}}$
‘not to be too large’). We study the probability of
![]() $\mathcal {F}$
by applying (12.6) (Gaussian approximation for
$\mathcal {F}$
by applying (12.6) (Gaussian approximation for
![]() $E_{\mathrm {shift}(1)}$
) as well as Claim 12.2 together with Markov’s inequality (as in the upper bound proof in the previous step).
$E_{\mathrm {shift}(1)}$
) as well as Claim 12.2 together with Markov’s inequality (as in the upper bound proof in the previous step).
Let
![]() $s\in \{-1,1\}$
be as in Claim 12.1(2). For any
$s\in \{-1,1\}$
be as in Claim 12.1(2). For any
![]() $0<K<n^{3/2}/(2\sigma )$
, we can consider the event that
$0<K<n^{3/2}/(2\sigma )$
, we can consider the event that
![]() $K\sigma \le s(x'-E_{\mathrm {shift}(1)})\le 2K\sigma $
, which can be interpreted as the event that
$K\sigma \le s(x'-E_{\mathrm {shift}(1)})\le 2K\sigma $
, which can be interpreted as the event that
![]() $E_{\mathrm {shift}(1)}$
lies in a certain interval of length
$E_{\mathrm {shift}(1)}$
lies in a certain interval of length
![]() $K\sigma $
whose endpoints both have absolute value at most
$K\sigma $
whose endpoints both have absolute value at most
![]() $|x'|+2K\sigma \le (A+2)n^{3/2}$
. Using (12.6), we can compare the probability for this event to the probability that a normal random variable with distribution
$|x'|+2K\sigma \le (A+2)n^{3/2}$
. Using (12.6), we can compare the probability for this event to the probability that a normal random variable with distribution
![]() $\mathcal N(0,(\frac 12\|Q\vec y\|_2)^2)$
lies in this interval. In this way, we see that the probability of the event
$\mathcal N(0,(\frac 12\|Q\vec y\|_2)^2)$
lies in this interval. In this way, we see that the probability of the event
![]() $K\sigma \le s(x'-E_{\mathrm {shift}(1)})\le 2K\sigma $
is at least
$K\sigma \le s(x'-E_{\mathrm {shift}(1)})\le 2K\sigma $
is at least
 $$ \begin{align} K\sigma\cdot \frac{\exp(-(A+2)^2n^3/(\frac12\lVert Q\vec{y}\rVert_2^2))}{\sqrt{2\pi}\cdot \frac{1}{2}\lVert Q\vec{y}\rVert_2}-O_{C,H}(1/\sqrt{n})\ge K\sigma\cdot \frac{\exp(-O_{C,A}(1))}{O_H(n^{3/2})}-O_{C,H}(1/\sqrt{n}), \end{align} $$
$$ \begin{align} K\sigma\cdot \frac{\exp(-(A+2)^2n^3/(\frac12\lVert Q\vec{y}\rVert_2^2))}{\sqrt{2\pi}\cdot \frac{1}{2}\lVert Q\vec{y}\rVert_2}-O_{C,H}(1/\sqrt{n})\ge K\sigma\cdot \frac{\exp(-O_{C,A}(1))}{O_H(n^{3/2})}-O_{C,H}(1/\sqrt{n}), \end{align} $$
where we used that
![]() $\lVert Q\vec {y}\rVert _2\gtrsim _C n^{3/2}$
and
$\lVert Q\vec {y}\rVert _2\gtrsim _C n^{3/2}$
and
![]() $\lVert Q\vec {y}\rVert _{\infty }\le (H+2)n$
(which implies that
$\lVert Q\vec {y}\rVert _{\infty }\le (H+2)n$
(which implies that
![]() $\lVert Q\vec {y}\rVert _2\lesssim _H n^{3/2}$
), as discussed in Step 5.
$\lVert Q\vec {y}\rVert _2\lesssim _H n^{3/2}$
), as discussed in Step 5.
Now, recalling that
![]() $n^{1.05}\ge \sigma \ge \lVert M^*\rVert _{\mathrm F}\gtrsim _C n$
from Step 5, we can take
$n^{1.05}\ge \sigma \ge \lVert M^*\rVert _{\mathrm F}\gtrsim _C n$
from Step 5, we can take
![]() $K=K(C,H,A)\ge 10^4$
to be a sufficiently large constant such that the right-hand-side of (12.11) is at least
$K=K(C,H,A)\ge 10^4$
to be a sufficiently large constant such that the right-hand-side of (12.11) is at least
![]() $\sigma /n^{3/2}$
such that
$\sigma /n^{3/2}$
such that
![]() $\lVert M^*\rVert _{\mathrm F}\ge K^{-1/4}\cdot n$
, and such that the hidden constant in the
$\lVert M^*\rVert _{\mathrm F}\ge K^{-1/4}\cdot n$
, and such that the hidden constant in the
![]() $\lesssim _{C,H}$
notation in the statement of Claim 12.2 is at most
$\lesssim _{C,H}$
notation in the statement of Claim 12.2 is at most
![]() $K^{1/4}$
. By the choice of K, we have
$K^{1/4}$
. By the choice of K, we have
Furthermore, using Claim 12.2 and Markov’s inequality we have
Thus, with probability at least
![]() $\sigma /(2n^{3/2})$
, we have
$\sigma /(2n^{3/2})$
, we have
![]() $E_{\mathrm {shift}(2)}^2+\sigma _{\mathrm {shift}}^2\le 2K^{5/4}n^2$
and
$E_{\mathrm {shift}(2)}^2+\sigma _{\mathrm {shift}}^2\le 2K^{5/4}n^2$
and
![]() $K\sigma \le s(x'-E_{\mathrm {shift}(1)})\le 2K\sigma $
. Let
$K\sigma \le s(x'-E_{\mathrm {shift}(1)})\le 2K\sigma $
. Let
![]() $\mathcal {F}$
be the event that these two conditions are satisfied and
$\mathcal {F}$
be the event that these two conditions are satisfied and
![]() $\vec {\Delta }$
is near-balanced (and note that
$\vec {\Delta }$
is near-balanced (and note that
![]() $\mathcal {F}$
only depends on the randomness of
$\mathcal {F}$
only depends on the randomness of
![]() $\vec {\Delta }$
). Recalling from Step 4 that
$\vec {\Delta }$
). Recalling from Step 4 that
![]() $\vec {\Delta }$
is near-balanced with probability
$\vec {\Delta }$
is near-balanced with probability
![]() $1-n^{-\omega (1)}$
, we see that
$1-n^{-\omega (1)}$
, we see that
![]() $\Pr [\mathcal F]\geq \sigma /(4n^{3/2})$
.
$\Pr [\mathcal F]\geq \sigma /(4n^{3/2})$
.
We claim that whenever
![]() $\mathcal {F}$
holds, we have
$\mathcal {F}$
holds, we have
![]() $\sigma /K^2\le \sigma _{\vec {\Delta }}\le K^2\sigma $
and
$\sigma /K^2\le \sigma _{\vec {\Delta }}\le K^2\sigma $
and
![]() $3n\le s(x-E_{\vec {\Delta }})\le 3K^3\sigma _{\vec {\Delta }}$
. For the first claim, note that if
$3n\le s(x-E_{\vec {\Delta }})\le 3K^3\sigma _{\vec {\Delta }}$
. For the first claim, note that if
![]() $\mathcal {F}$
holds, then
$\mathcal {F}$
holds, then
![]() $\sigma _{\mathrm {shift}}^2\le 2K^{5/4}n^2\le K^2n^2/4$
and hence
$\sigma _{\mathrm {shift}}^2\le 2K^{5/4}n^2\le K^2n^2/4$
and hence
![]() $\sigma _{\vec {\Delta }}^2\geq \sigma ^2/2-\sigma _{\mathrm {shift}}^2\geq \sigma ^2/2-K^2n^2/4$
. So, if
$\sigma _{\vec {\Delta }}^2\geq \sigma ^2/2-\sigma _{\mathrm {shift}}^2\geq \sigma ^2/2-K^2n^2/4$
. So, if
![]() $\sigma \geq Kn$
, we obtain the desired lower bound
$\sigma \geq Kn$
, we obtain the desired lower bound
![]() $\sigma _{\vec {\Delta }}\geq \sigma /2\geq \sigma /K^2$
. If
$\sigma _{\vec {\Delta }}\geq \sigma /2\geq \sigma /K^2$
. If
![]() $\sigma \leq Kn$
, then we instead obtain the desired lower bound on
$\sigma \leq Kn$
, then we instead obtain the desired lower bound on
![]() $\sigma _{\vec {\Delta }}$
by observing that
$\sigma _{\vec {\Delta }}$
by observing that
![]() $\sigma \leq Kn\le K^2 \lVert M^*\rVert _{\mathrm F}\le K^2 \sigma _{\vec {\Delta }}$
(using that
$\sigma \leq Kn\le K^2 \lVert M^*\rVert _{\mathrm F}\le K^2 \sigma _{\vec {\Delta }}$
(using that
![]() $\vec {\Delta }$
is near-balanced). For the upper bound on
$\vec {\Delta }$
is near-balanced). For the upper bound on
![]() $\sigma _{\vec {\Delta }}$
, recall from the end of Step 5 that we have
$\sigma _{\vec {\Delta }}$
, recall from the end of Step 5 that we have
![]() $\sigma _{\vec {\Delta }}\le 2\sigma \le K^2\sigma $
or
$\sigma _{\vec {\Delta }}\le 2\sigma \le K^2\sigma $
or
![]() $\sigma _{\vec {\Delta }}\le 2\sigma _{\mathrm {shift}}$
. In the latter case, we obtain
$\sigma _{\vec {\Delta }}\le 2\sigma _{\mathrm {shift}}$
. In the latter case, we obtain
![]() $\sigma _{\vec {\Delta }}\le 2\sigma _{\mathrm {shift}}\le Kn\le K^{2}\lVert M^*\rVert _{\mathrm F}\le K^2\sigma $
. Altogether, we have proved that
$\sigma _{\vec {\Delta }}\le 2\sigma _{\mathrm {shift}}\le Kn\le K^{2}\lVert M^*\rVert _{\mathrm F}\le K^2\sigma $
. Altogether, we have proved that
![]() $\sigma /K^2\le \sigma _{\vec {\Delta }}\le K^2\sigma $
whenever
$\sigma /K^2\le \sigma _{\vec {\Delta }}\le K^2\sigma $
whenever
![]() $\mathcal {F}$
holds, as claimed.
$\mathcal {F}$
holds, as claimed.
For the second of our two claims, note that whenever
![]() $\mathcal {F}$
holds, we have
$\mathcal {F}$
holds, we have
![]() $E_{\mathrm {shift}(2)}^2\le 2K^{5/4}n^2\le 2K^{7/4}\lVert M^*\rVert _{\mathrm F}^2\le K^2\sigma ^2/4$
, so
$E_{\mathrm {shift}(2)}^2\le 2K^{5/4}n^2\le 2K^{7/4}\lVert M^*\rVert _{\mathrm F}^2\le K^2\sigma ^2/4$
, so
![]() $|E_{\mathrm {shift}(2)}|\le K\sigma /2$
and hence
$|E_{\mathrm {shift}(2)}|\le K\sigma /2$
and hence
![]() $K\sigma /2 \le s(x'-E_{\mathrm {shift}(1)}-E_{\mathrm {shift}(2)})\le 2.5K\sigma $
. Recalling (12.5) and
$K\sigma /2 \le s(x'-E_{\mathrm {shift}(1)}-E_{\mathrm {shift}(2)})\le 2.5K\sigma $
. Recalling (12.5) and
![]() $x'=x-E$
, this implies the desired claim
$x'=x-E$
, this implies the desired claim
where in the first and fourth inequalities we used that
![]() $n\leq K^{1/4}\lVert M^*\rVert _{\mathrm F}\le K^{1/4}\sigma $
, and in the last inequality we used the first claim.
$n\leq K^{1/4}\lVert M^*\rVert _{\mathrm F}\le K^{1/4}\sigma $
, and in the last inequality we used the first claim.
Now, having established the above claims for all outcomes of
![]() $\vec {\Delta }$
satisfying
$\vec {\Delta }$
satisfying
![]() $\mathcal {F}$
, Claim 12.1(2) implies that
$\mathcal {F}$
, Claim 12.1(2) implies that
![]() $\Pr [\mathcal E| \mathcal F]\gtrsim _{C,H,A} 1/(K^2\sigma )$
. Thus,
$\Pr [\mathcal E| \mathcal F]\gtrsim _{C,H,A} 1/(K^2\sigma )$
. Thus,
![]() $\Pr [\mathcal E]\ge \Pr [\mathcal F]\cdot \Pr [\mathcal E|\mathcal F]\gtrsim _{C,H,A} \sigma /(4n^{3/2})\cdot 1/(K^2\sigma )\gtrsim _{C,H,A}n^{-3/2}$
, completing the proof of the lower bound.
$\Pr [\mathcal E]\ge \Pr [\mathcal F]\cdot \Pr [\mathcal E|\mathcal F]\gtrsim _{C,H,A} \sigma /(4n^{3/2})\cdot 1/(K^2\sigma )\gtrsim _{C,H,A}n^{-3/2}$
, completing the proof of the lower bound.
12.1 Proofs of claims
In order to finish the proof of Theorem 3.1 in the
![]() $\gamma $
-structured case, it remains to prove Claims 12.1 and 12.2.
$\gamma $
-structured case, it remains to prove Claims 12.1 and 12.2.
Proof of Claim 12.1
Recall that in the statement of Claim 12.1 we fixed a near-balanced outcome of
![]() $\vec {\Delta }$
and the desired conclusions are conditional on this outcome of
$\vec {\Delta }$
and the desired conclusions are conditional on this outcome of
![]() $\vec {\Delta }$
. Throughout this proof, let us therefore always condition on the fixed outcome of
$\vec {\Delta }$
. Throughout this proof, let us therefore always condition on the fixed outcome of
![]() $\vec {\Delta }$
, which we now view as being nonrandom, and for notational simplicity we omit all ‘
$\vec {\Delta }$
, which we now view as being nonrandom, and for notational simplicity we omit all ‘
![]() $|\vec \Delta $
’ notation.
$|\vec \Delta $
’ notation.
Recall that we have
![]() $\sigma _{\vec {\Delta }}^{2}=2\|M^{*}\|_{\mathrm F}^{2}+\|\vec {w}^{*}_{\vec {\Delta }}\|_{2}^{2}+O(n^{7/4+14\gamma })$
and
$\sigma _{\vec {\Delta }}^{2}=2\|M^{*}\|_{\mathrm F}^{2}+\|\vec {w}^{*}_{\vec {\Delta }}\|_{2}^{2}+O(n^{7/4+14\gamma })$
and
![]() $\|\vec {w}^{*}_{\vec {\Delta }}\|_{\infty }\le n^{1/2+5\gamma }$
(since
$\|\vec {w}^{*}_{\vec {\Delta }}\|_{\infty }\le n^{1/2+5\gamma }$
(since
![]() $\vec {\Delta }$
is near-balanced). Also, recalling that all entries of
$\vec {\Delta }$
is near-balanced). Also, recalling that all entries of
![]() $M^*$
have absolute value at most
$M^*$
have absolute value at most
![]() $1$
, this implies
$1$
, this implies
![]() $\sigma _{\vec \Delta }^2\le n^2+n\cdot n^{1+10\gamma }+O(n^{7/4+14\gamma })\le n^{2.2}$
(as
$\sigma _{\vec \Delta }^2\le n^2+n\cdot n^{1+10\gamma }+O(n^{7/4+14\gamma })\le n^{2.2}$
(as
![]() $\gamma =10^{-4}$
). Thus,
$\gamma =10^{-4}$
). Thus,
![]() $\sigma _{\vec \Delta }\le n^{1.1}$
.
$\sigma _{\vec \Delta }\le n^{1.1}$
.
For the upper bound in (1), we will use Lemma 6.2 and for the lower bound in (2) we will use Lemma 6.3. Recalling (12.3), let Z be the ‘Gaussian analog’ of X: Let
![]() $\vec {z}\sim \mathcal {N}(0,1)^{\otimes n}$
be a standard n-variate Gaussian random vector, and let
$\vec {z}\sim \mathcal {N}(0,1)^{\otimes n}$
be a standard n-variate Gaussian random vector, and let
 $$\begin{align*}Z=\left(E+\frac{1}{2}\vec{y}\cdot\vec{\Delta}+\frac{1}{8}\vec{\Delta}^{\intercal}M\vec{\Delta}\right)+\vec{w}^{*}_{\vec{\Delta}}\cdot\vec{z}+\vec{z}^{\intercal}M^{*}\vec{z}.\end{align*}$$
$$\begin{align*}Z=\left(E+\frac{1}{2}\vec{y}\cdot\vec{\Delta}+\frac{1}{8}\vec{\Delta}^{\intercal}M\vec{\Delta}\right)+\vec{w}^{*}_{\vec{\Delta}}\cdot\vec{z}+\vec{z}^{\intercal}M^{*}\vec{z}.\end{align*}$$
Let
![]() $\nu =\nu (2C,0.001)>0$
be as in Lemma 8.1, and let
$\nu =\nu (2C,0.001)>0$
be as in Lemma 8.1, and let
![]() $\varepsilon =2/\nu $
. Let
$\varepsilon =2/\nu $
. Let
![]() $s \in \{-1, 1\}$
be the sign of the eigenvalue of
$s \in \{-1, 1\}$
be the sign of the eigenvalue of
![]() $M^*$
with the largest magnitude. We collect several estimates.
$M^*$
with the largest magnitude. We collect several estimates.
-
(A)
 $\sigma (Z)\asymp _{C}\sigma _{\vec \Delta }\gtrsim _{C} n$
and
$\sigma (Z)\asymp _{C}\sigma _{\vec \Delta }\gtrsim _{C} n$
and
 $|\mathbb E Z-E_{\vec \Delta }|\le 2n$
.
$|\mathbb E Z-E_{\vec \Delta }|\le 2n$
. -
(B) For all
 $x\in \mathbb {R}$
,
$x\in \mathbb {R}$
,  $$\begin{align*}\Pr[|Z-x|\le \varepsilon]\lesssim_{C}\frac{\varepsilon}{\sigma(Z)}\exp\left(-\Omega_{C}\left(\frac{|x-\mathbb E Z|}{\sigma(Z)}\right)\right)\le \frac\varepsilon{\sigma(Z)}.\end{align*}$$
$$\begin{align*}\Pr[|Z-x|\le \varepsilon]\lesssim_{C}\frac{\varepsilon}{\sigma(Z)}\exp\left(-\Omega_{C}\left(\frac{|x-\mathbb E Z|}{\sigma(Z)}\right)\right)\le \frac\varepsilon{\sigma(Z)}.\end{align*}$$
-
(C)
 $\int _{-2/\varepsilon }^{2/\varepsilon }|\varphi _{X}(\tau )-\varphi _{Z}(\tau )|\,d\tau \le n^{-1.2}$
.
$\int _{-2/\varepsilon }^{2/\varepsilon }|\varphi _{X}(\tau )-\varphi _{Z}(\tau )|\,d\tau \le n^{-1.2}$
. -
(D) For any fixed
 $A'\in \mathbb {R}_{\ge 0}$
, assuming that n is sufficiently large with respect to
$A'\in \mathbb {R}_{\ge 0}$
, assuming that n is sufficiently large with respect to
 $A'$
, we have
$A'$
, we have
 $p_{Z}(y_{1})/p_{Z}(y_{2})\le 2$
for all
$p_{Z}(y_{1})/p_{Z}(y_{2})\le 2$
for all
 $y_1,y_2\in \mathbb {R}$
with
$y_1,y_2\in \mathbb {R}$
with
 $0\le s (y_{1}-\mathbb E Z)\le A'\sigma (Z)$
and
$0\le s (y_{1}-\mathbb E Z)\le A'\sigma (Z)$
and
 $|y_{1}-y_{2}|\le 2n^{1/4}\varepsilon $
.
$|y_{1}-y_{2}|\le 2n^{1/4}\varepsilon $
. -
(E) For any fixed
 $A'>0$
and any
$A'>0$
and any
 $x\in \mathbb Z$
satisfying
$x\in \mathbb Z$
satisfying
 $0\le s(x-\mathbb E Z)\le A'\sigma (Z)$
,
$0\le s(x-\mathbb E Z)\le A'\sigma (Z)$
,  $$\begin{align*}\Pr[|Z-x|\le \varepsilon]\gtrsim_{C,A'}\frac{1}{\sigma(Z)}\qquad\text{and}\qquad p_Z(x)\gtrsim_{C,A'}\frac1{\sigma(Z)}.\end{align*}$$
$$\begin{align*}\Pr[|Z-x|\le \varepsilon]\gtrsim_{C,A'}\frac{1}{\sigma(Z)}\qquad\text{and}\qquad p_Z(x)\gtrsim_{C,A'}\frac1{\sigma(Z)}.\end{align*}$$
We will prove (A–E) using the results from Sections 11, 8, 10 and 5; before explaining how to do this, we deduce the desired upper and lower bounds in (1) and (2). Let
![]() $B=B(C)=10^4\cdot 2\varepsilon $
. First, using that by (A) we have
$B=B(C)=10^4\cdot 2\varepsilon $
. First, using that by (A) we have
![]() $\varepsilon \le \sigma (Z)$
for sufficiently large n, and using (B), we can apply Lemma 6.2 to
$\varepsilon \le \sigma (Z)$
for sufficiently large n, and using (B), we can apply Lemma 6.2 to
![]() $X-\mathbb EZ$
and
$X-\mathbb EZ$
and
![]() $Z-\mathbb E Z$
and
$Z-\mathbb E Z$
and
![]() $\sigma (Z)$
. Hence, for all
$\sigma (Z)$
. Hence, for all
![]() $x\in \mathbb Z$
we have
$x\in \mathbb Z$
we have
 $$ \begin{align*} \Pr[|X-x|\leq B]&\le 2\cdot 10^4\sup_{\substack{y\in\mathbb{R}\\|x-y|\le B}}\Pr[|X-y|\leq \varepsilon]\\ &\lesssim_{C} \frac{\varepsilon^2}{\sigma(Z)^2}+ \frac{\varepsilon}{\sigma(Z)}\exp\left(-\Omega_{C}\left(\frac{|x-\mathbb E Z|}{\sigma(Z)}\right)\right)+\varepsilon \int_{-2/\varepsilon}^{2/\varepsilon}|\varphi_X(\tau)-\varphi_Z(\tau)|\,d\tau. \end{align*} $$
$$ \begin{align*} \Pr[|X-x|\leq B]&\le 2\cdot 10^4\sup_{\substack{y\in\mathbb{R}\\|x-y|\le B}}\Pr[|X-y|\leq \varepsilon]\\ &\lesssim_{C} \frac{\varepsilon^2}{\sigma(Z)^2}+ \frac{\varepsilon}{\sigma(Z)}\exp\left(-\Omega_{C}\left(\frac{|x-\mathbb E Z|}{\sigma(Z)}\right)\right)+\varepsilon \int_{-2/\varepsilon}^{2/\varepsilon}|\varphi_X(\tau)-\varphi_Z(\tau)|\,d\tau. \end{align*} $$
The bound in (1) then follows from (A) and (C). Second, by (A) and (E), if
![]() $x\in \mathbb {Z}$
satisfies
$x\in \mathbb {Z}$
satisfies
![]() $3n\le s(x-E_{\vec \Delta })\le A\sigma _{\vec \Delta }$
then
$3n\le s(x-E_{\vec \Delta })\le A\sigma _{\vec \Delta }$
then
![]() $\Pr [|Z-x|\le \varepsilon ]\gtrsim _{C,A} 1/\sigma _{\vec \Delta }$
. Furthermore, for all
$\Pr [|Z-x|\le \varepsilon ]\gtrsim _{C,A} 1/\sigma _{\vec \Delta }$
. Furthermore, for all
![]() $y_1,y_2\in [x-n^{1/4}\varepsilon ,x+n^{1/4}\varepsilon ]$
by (A) we have
$y_1,y_2\in [x-n^{1/4}\varepsilon ,x+n^{1/4}\varepsilon ]$
by (A) we have
![]() $0\le 3n-|\mathbb E Z-E_{\vec \Delta }|-n^{1/4}\varepsilon \le s (y_{1}-\mathbb E Z)\le A'\sigma (Z)$
for some
$0\le 3n-|\mathbb E Z-E_{\vec \Delta }|-n^{1/4}\varepsilon \le s (y_{1}-\mathbb E Z)\le A'\sigma (Z)$
for some
![]() $A'=A'(C,A)$
, and therefore
$A'=A'(C,A)$
, and therefore
![]() $p_{Z}(y_{1})/p_{Z}(y_{2})\le 2$
by (D). Let
$p_{Z}(y_{1})/p_{Z}(y_{2})\le 2$
by (D). Let
![]() $K=2$
and
$K=2$
and
![]() $R=n^{1/4}$
, so by Lemma 6.3 we have (recalling that
$R=n^{1/4}$
, so by Lemma 6.3 we have (recalling that
![]() $B=10^4\cdot 2\varepsilon =10^4K\varepsilon $
)
$B=10^4\cdot 2\varepsilon =10^4K\varepsilon $
)
 $$ \begin{align*} \Pr[|X-x|\leq B]&\ge \Omega_{C,A}(1/\sigma_{\vec \Delta})-C_{6.3}\left(R^{-1}\mathcal L(Z,\varepsilon)+\varepsilon\int_{-2/\varepsilon}^{2/\varepsilon}|\varphi_X(\tau)-\varphi_Z(\tau)|\,d\tau\right). \end{align*} $$
$$ \begin{align*} \Pr[|X-x|\leq B]&\ge \Omega_{C,A}(1/\sigma_{\vec \Delta})-C_{6.3}\left(R^{-1}\mathcal L(Z,\varepsilon)+\varepsilon\int_{-2/\varepsilon}^{2/\varepsilon}|\varphi_X(\tau)-\varphi_Z(\tau)|\,d\tau\right). \end{align*} $$
The bound in (2) then follows from (A–C).
Now, we prove (A–E). First, note that for any matrix
![]() $\widetilde M\in \mathbb {R}^{V\times V}$
with rank at most say 400, we have
$\widetilde M\in \mathbb {R}^{V\times V}$
with rank at most say 400, we have
![]() $\|M^{*}-\widetilde {M}\|_{\mathrm {F}}^{2}=\frac {1}{64}\|M-(MQ+QM-QMQ+64\widetilde {M})\|_{\mathrm {F}}^{2}\gtrsim _{C} n^{2}\ge \|M^{*}\|_{\mathrm {F}}^{2}$
by Lemma 10.1. Also, note that
$\|M^{*}-\widetilde {M}\|_{\mathrm {F}}^{2}=\frac {1}{64}\|M-(MQ+QM-QMQ+64\widetilde {M})\|_{\mathrm {F}}^{2}\gtrsim _{C} n^{2}\ge \|M^{*}\|_{\mathrm {F}}^{2}$
by Lemma 10.1. Also, note that
![]() $M^*$
and
$M^*$
and
![]() $\vec {w}^{*}_{\vec {\Delta }}$
satisfy conditions (a)–(d) in Lemma 11.1 for
$\vec {w}^{*}_{\vec {\Delta }}$
satisfy conditions (a)–(d) in Lemma 11.1 for
![]() $\delta =2\gamma =2\cdot 10^{-4}$
, as discussed at the end of Step 3 and the start of Step 4 above.
$\delta =2\gamma =2\cdot 10^{-4}$
, as discussed at the end of Step 3 and the start of Step 4 above.
Then, the two parts of (A) follow from parts (1) and (2) of Lemma 11.1 (applied with
![]() $\delta =2\gamma =2\cdot 10^{-4}$
), recalling
$\delta =2\gamma =2\cdot 10^{-4}$
), recalling
![]() $\sigma _{\vec {\Delta }}\gtrsim _C n$
from the end of Step 4. Furthermore, (B) and (E) follow from Theorem 5.2(1–2) (for the second part of (E), we use Theorem 5.2(2) with
$\sigma _{\vec {\Delta }}\gtrsim _C n$
from the end of Step 4. Furthermore, (B) and (E) follow from Theorem 5.2(1–2) (for the second part of (E), we use Theorem 5.2(2) with
![]() $\varepsilon \to 0$
).
$\varepsilon \to 0$
).
Now, consider
![]() $y_1,y_2$
as in (D), so in particular
$y_1,y_2$
as in (D), so in particular
![]() $|y_{1}-y_{2}|\le 2n^{1/4}\varepsilon $
. By the inversion formula (4.1) and Lemma 5.11 (with
$|y_{1}-y_{2}|\le 2n^{1/4}\varepsilon $
. By the inversion formula (4.1) and Lemma 5.11 (with
![]() $r=8$
), and (A), we have
$r=8$
), and (A), we have
 $$ \begin{align*} |p_{Z}(y_{1})-p_{Z}(y_{2})| & =\left|\frac{1}{2\pi}\int_{-\infty}^{\infty}(e^{-i\tau y_{1}}-e^{-i\tau y_{2}})\mathbb E e^{i\tau Z}\,d\tau\right|\lesssim\int_{-\infty}^{\infty}\min\{|\tau(y_{1}-y_{2})|,1\}|\mathbb E e^{i\tau Z}|\,d\tau\\[4pt] & \lesssim_{C}\int_{-\infty}^{\infty}\min\{n^{1/4}|\tau|,1\}\cdot(1+\tau^{2}n^{2})^{-2}\,d\tau\lesssim n^{-7/4}=o(1/\sigma(Z)), \end{align*} $$
$$ \begin{align*} |p_{Z}(y_{1})-p_{Z}(y_{2})| & =\left|\frac{1}{2\pi}\int_{-\infty}^{\infty}(e^{-i\tau y_{1}}-e^{-i\tau y_{2}})\mathbb E e^{i\tau Z}\,d\tau\right|\lesssim\int_{-\infty}^{\infty}\min\{|\tau(y_{1}-y_{2})|,1\}|\mathbb E e^{i\tau Z}|\,d\tau\\[4pt] & \lesssim_{C}\int_{-\infty}^{\infty}\min\{n^{1/4}|\tau|,1\}\cdot(1+\tau^{2}n^{2})^{-2}\,d\tau\lesssim n^{-7/4}=o(1/\sigma(Z)), \end{align*} $$
from which we may deduce (D) using the second part of (E). It remains to prove (C), that is, to bound the integral
![]() $\int _{-2/\varepsilon }^{2/\varepsilon }|\varphi _{X}(\tau )-\varphi _{Z}(\tau )|\,d\tau $
by
$\int _{-2/\varepsilon }^{2/\varepsilon }|\varphi _{X}(\tau )-\varphi _{Z}(\tau )|\,d\tau $
by
![]() $n^{-1.2}$
. If
$n^{-1.2}$
. If
![]() $|\tau |\le n^{-0.99}$
, then by Lemma 11.1(3) (with
$|\tau |\le n^{-0.99}$
, then by Lemma 11.1(3) (with
![]() $\delta =2\gamma $
) we have
$\delta =2\gamma $
) we have
![]() $|\varphi _{X}(\tau )-\varphi _{Z}(\tau )|\lesssim |\tau |^4\cdot n^{3+24\gamma }+|\tau |\cdot n^{3/4+8\gamma }\lesssim |\tau |\cdot n^{3/4+8\gamma }$
. Thus, the contribution of the range
$|\varphi _{X}(\tau )-\varphi _{Z}(\tau )|\lesssim |\tau |^4\cdot n^{3+24\gamma }+|\tau |\cdot n^{3/4+8\gamma }\lesssim |\tau |\cdot n^{3/4+8\gamma }$
. Thus, the contribution of the range
![]() $|\tau |\le n^{-0.99}$
to the integral
$|\tau |\le n^{-0.99}$
to the integral
![]() $ \int _{-2/\varepsilon }^{2/\varepsilon }|\varphi _{X}(\tau )-\varphi _{Z}(\tau )|\,d\tau $
is
$ \int _{-2/\varepsilon }^{2/\varepsilon }|\varphi _{X}(\tau )-\varphi _{Z}(\tau )|\,d\tau $
is
![]() $O((n^{-0.99})^2 \cdot n^{3/4+8\gamma })=O(n^{-1.23+8\gamma })$
, which is smaller than
$O((n^{-0.99})^2 \cdot n^{3/4+8\gamma })=O(n^{-1.23+8\gamma })$
, which is smaller than
![]() $n^{-1.2}/2$
(recalling that
$n^{-1.2}/2$
(recalling that
![]() $\gamma =10^{-4}$
).
$\gamma =10^{-4}$
).
For
![]() $n^{-0.99}\le |\tau |\le 2/\varepsilon $
, we bound
$n^{-0.99}\le |\tau |\le 2/\varepsilon $
, we bound
![]() $|\varphi _X(\tau )|$
and
$|\varphi _X(\tau )|$
and
![]() $|\varphi _Z(\tau )|$
separately. By Lemma 5.11 (with
$|\varphi _Z(\tau )|$
separately. By Lemma 5.11 (with
![]() $r=400$
), we have
$r=400$
), we have
![]() $|\varphi _Z(\tau )|\lesssim _C (1+\tau ^2n^2)^{-100}\le (n^{0.02})^{-100}=n^{-2}$
. To bound
$|\varphi _Z(\tau )|\lesssim _C (1+\tau ^2n^2)^{-100}\le (n^{0.02})^{-100}=n^{-2}$
. To bound
![]() $|\varphi _X(\tau )|$
, we use Lemma 8.1, after conditioning on any outcome of
$|\varphi _X(\tau )|$
, we use Lemma 8.1, after conditioning on any outcome of
![]() $U\cap (I_2\cup \cdots \cup I_m)$
. After this conditioning, the remaining randomness is just within the first bucket
$U\cap (I_2\cup \cdots \cup I_m)$
. After this conditioning, the remaining randomness is just within the first bucket
![]() $I_1$
, and conditionally X is of the form required to apply Lemma 8.1 with respect to the
$I_1$
, and conditionally X is of the form required to apply Lemma 8.1 with respect to the
![]() $(2C)$
-Ramsey graph
$(2C)$
-Ramsey graph
![]() $G[I_1]$
of size
$G[I_1]$
of size
![]() $|I_1|\geq n^{1-2\gamma }$
, and we obtain
$|I_1|\geq n^{1-2\gamma }$
, and we obtain
![]() $|\varphi _X(\tau )|\lesssim n^{-(1-2\gamma )5}\le n^{-4}$
since
$|\varphi _X(\tau )|\lesssim n^{-(1-2\gamma )5}\le n^{-4}$
since
![]() $|\tau |\ge n^{-0.99}\ge |I_1|^{-0.999}$
. Thus, in the range
$|\tau |\ge n^{-0.99}\ge |I_1|^{-0.999}$
. Thus, in the range
![]() $n^{-0.99}\le |\tau |\le 2/\varepsilon $
we have
$n^{-0.99}\le |\tau |\le 2/\varepsilon $
we have
![]() $|\varphi _{X}(\tau )-\varphi _{Z}(\tau )|\le |\varphi _X(\tau )|+|\varphi _Z(\tau )|\lesssim n^{-2}$
, and so the contribution of this range to the integral
$|\varphi _{X}(\tau )-\varphi _{Z}(\tau )|\le |\varphi _X(\tau )|+|\varphi _Z(\tau )|\lesssim n^{-2}$
, and so the contribution of this range to the integral
![]() $\int _{-2/\varepsilon }^{2/\varepsilon }|\varphi _{X}(\tau )-\varphi _{Z}(\tau )|\,d\tau $
is also smaller than
$\int _{-2/\varepsilon }^{2/\varepsilon }|\varphi _{X}(\tau )-\varphi _{Z}(\tau )|\,d\tau $
is also smaller than
![]() $n^{-1.2}/2$
.
$n^{-1.2}/2$
.
We will deduce Claim 12.2 from the following auxiliary estimate, applied with
![]() $k=1$
and with
$k=1$
and with
![]() $k=2$
(recall that the functions
$k=2$
(recall that the functions
![]() $\psi $
and f already appeared in the proof of Lemma 6.1).
$\psi $
and f already appeared in the proof of Lemma 6.1).
Claim 12.3. Fix
![]() $k\in \mathbb {N}$
. Let us define the function
$k\in \mathbb {N}$
. Let us define the function
![]() $\psi \colon \mathbb {R}\to \mathbb {R}$
as the convolution
$\psi \colon \mathbb {R}\to \mathbb {R}$
as the convolution
![]() (where
(where
![]() is the indicator function of the interval
is the indicator function of the interval
![]() $[-1,1]$
) and let
$[-1,1]$
) and let
![]() $f=\hat {\psi }$
be the Fourier transform of
$f=\hat {\psi }$
be the Fourier transform of
![]() $\psi $
. Consider a matrix
$\psi $
. Consider a matrix
![]() $A\in \mathbb {R}^{V\times V}$
whose entries have absolute value at most
$A\in \mathbb {R}^{V\times V}$
whose entries have absolute value at most
![]() $1$
, and a vector
$1$
, and a vector
![]() $\vec {\beta }\in \mathbb {R}^{V}$
with
$\vec {\beta }\in \mathbb {R}^{V}$
with
![]() $\|\vec {\beta }\|_{\infty }\le \pi /4$
. Then for any
$\|\vec {\beta }\|_{\infty }\le \pi /4$
. Then for any
![]() $t\in \mathbb {R}$
we have
$t\in \mathbb {R}$
we have
![]() $|\mathbb E[(\vec {x}^{\intercal }A\vec {x})^{k}f(\vec {\beta }\cdot \vec {x}-t)]|\lesssim _{k}(\sqrt {n}/\lVert \vec {\beta }\rVert _2)^{2k+1}\cdot n^{k-1/2}$
.
$|\mathbb E[(\vec {x}^{\intercal }A\vec {x})^{k}f(\vec {\beta }\cdot \vec {x}-t)]|\lesssim _{k}(\sqrt {n}/\lVert \vec {\beta }\rVert _2)^{2k+1}\cdot n^{k-1/2}$
.
Proof. Observing that
![]() $x_{v}^{2}=1$
, we can express
$x_{v}^{2}=1$
, we can express
![]() $(\vec {x}^{\intercal }A\vec {x})^{k}$
as a multilinear polynomial of degree at most
$(\vec {x}^{\intercal }A\vec {x})^{k}$
as a multilinear polynomial of degree at most
![]() $2k$
in the
$2k$
in the
![]() $|V|\le n$
variables
$|V|\le n$
variables
![]() $x_v$
for
$x_v$
for
![]() $v\in V$
. For each
$v\in V$
. For each
![]() $\ell \leq 2k$
, this polynomial has at most
$\ell \leq 2k$
, this polynomial has at most
![]() $O(n^\ell )$
terms of degree
$O(n^\ell )$
terms of degree
![]() $\ell $
, and for each such term the corresponding coefficient has absolute value at most
$\ell $
, and for each such term the corresponding coefficient has absolute value at most
![]() $O_k(n^{(2k-\ell )/2})$
.
$O_k(n^{(2k-\ell )/2})$
.
It suffices to prove that
![]() $|\mathbb E[x_{v_{1}}\cdots x_{v_{\ell }}f(\vec {\beta }\cdot \vec {x}-t)]|\lesssim _{\ell }\lVert \beta \rVert _2^{-(\ell +1)}$
for any
$|\mathbb E[x_{v_{1}}\cdots x_{v_{\ell }}f(\vec {\beta }\cdot \vec {x}-t)]|\lesssim _{\ell }\lVert \beta \rVert _2^{-(\ell +1)}$
for any
![]() $\ell \le 2k$
and any distinct
$\ell \le 2k$
and any distinct
![]() $v_{1},\ldots ,v_{\ell }\in V$
. Indeed, this does imply
$v_{1},\ldots ,v_{\ell }\in V$
. Indeed, this does imply
![]() $|\mathbb E[(\vec {x}^{\intercal }A\vec {x})^{k}f(\vec {\beta }\cdot \vec {x}-t)]|\lesssim _k \sum _{\ell =0}^{2k} n^\ell \cdot n^{(2k-\ell )/2}\cdot \lVert \beta \rVert _2^{-(\ell +1)}\lesssim _k (\sqrt {n}/\lVert \vec {\beta }\rVert _2)^{2k+1}\cdot n^{k-1/2}$
using that
$|\mathbb E[(\vec {x}^{\intercal }A\vec {x})^{k}f(\vec {\beta }\cdot \vec {x}-t)]|\lesssim _k \sum _{\ell =0}^{2k} n^\ell \cdot n^{(2k-\ell )/2}\cdot \lVert \beta \rVert _2^{-(\ell +1)}\lesssim _k (\sqrt {n}/\lVert \vec {\beta }\rVert _2)^{2k+1}\cdot n^{k-1/2}$
using that
![]() $\lVert \vec {\beta }\rVert _2\le \sqrt {n}$
since
$\lVert \vec {\beta }\rVert _2\le \sqrt {n}$
since
![]() $|V|\le n$
and
$|V|\le n$
and
![]() $\|\vec {\beta }\|_{\infty }\le \pi /4\le 1$
.
$\|\vec {\beta }\|_{\infty }\le \pi /4\le 1$
.
Note that the support of the function
![]() $\psi $
is inside the interval
$\psi $
is inside the interval
![]() $[-2,2]$
and we furthermore have
$[-2,2]$
and we furthermore have
![]() $0\le \psi (\theta )\le 2$
for all
$0\le \psi (\theta )\le 2$
for all
![]() $\theta \in \mathbb {R}$
. Therefore, we can write
$\theta \in \mathbb {R}$
. Therefore, we can write
 $$ \begin{align*}|\mathbb E[x_{v_{1}}\cdots x_{v_{\ell}}f(\vec{\beta}\cdot\vec{x}-t)]| &=\left|\mathbb E\left[\int_{-\infty}^{\infty}x_{v_{1}}\cdots x_{v_{\ell}}\psi(\theta)e^{-i\theta(\vec{\beta}\cdot\vec{x}-t)}\,d\theta\right]\right|\\[4pt] &\le2\int_{-2}^{2}|\mathbb E[x_{v_{1}}\cdots x_{v_{\ell}}e^{-i\theta(\vec{\beta}\cdot\vec{x})}]|\,d\theta.\end{align*} $$
$$ \begin{align*}|\mathbb E[x_{v_{1}}\cdots x_{v_{\ell}}f(\vec{\beta}\cdot\vec{x}-t)]| &=\left|\mathbb E\left[\int_{-\infty}^{\infty}x_{v_{1}}\cdots x_{v_{\ell}}\psi(\theta)e^{-i\theta(\vec{\beta}\cdot\vec{x}-t)}\,d\theta\right]\right|\\[4pt] &\le2\int_{-2}^{2}|\mathbb E[x_{v_{1}}\cdots x_{v_{\ell}}e^{-i\theta(\vec{\beta}\cdot\vec{x})}]|\,d\theta.\end{align*} $$
By (4.2), for
![]() $-\pi /2\le \lambda \le \pi /2$
and
$-\pi /2\le \lambda \le \pi /2$
and
![]() $v\in V$
we have
$v\in V$
we have
![]() $|\mathbb E[e^{i\lambda x_{v}}]|=|\cos \lambda |\le \exp (-\lambda ^{2}/\pi ^2)$
, and
$|\mathbb E[e^{i\lambda x_{v}}]|=|\cos \lambda |\le \exp (-\lambda ^{2}/\pi ^2)$
, and
 $$\begin{align*}|\mathbb E[x_{v}e^{i\lambda x_{v}}]|=\left|\frac{1}{2}\exp(i\lambda)-\frac{1}{2}\exp(-i\lambda)\right|=|\sin \lambda|\le|\lambda|.\end{align*}$$
$$\begin{align*}|\mathbb E[x_{v}e^{i\lambda x_{v}}]|=\left|\frac{1}{2}\exp(i\lambda)-\frac{1}{2}\exp(-i\lambda)\right|=|\sin \lambda|\le|\lambda|.\end{align*}$$
Since
![]() $|\theta \beta _{v}|\le \pi /2$
for all
$|\theta \beta _{v}|\le \pi /2$
for all
![]() $v\in V$
and
$v\in V$
and
![]() $-2\le \theta \le 2$
, we can deduce (also using that
$-2\le \theta \le 2$
, we can deduce (also using that
![]() $|\beta _{v}|\le 1$
for all
$|\beta _{v}|\le 1$
for all
![]() $v\in V$
)
$v\in V$
)
 $$ \begin{align*} &|\mathbb E[x_{v_{1}}\cdots x_{v_{\ell}}f(\vec{\beta}\cdot\vec{x}-t)]| \\ &\qquad\qquad\le2\int_{-2}^{2}\prod_{j=1}^{\ell}|\theta \beta_{v_j}| \prod_{v\in V\setminus\{v_{1},\ldots,v_{\ell}\}}e^{-(\theta^2/\pi^2)\beta_v^2}\le 2 \int_{-2}^{2}|\theta|^{\ell}e^{-(\theta^{2}/\pi^2)(\lVert\vec{\beta}\rVert_2^2-\ell)}d\theta\\ &\qquad\qquad\lesssim_{\ell}\int_{-2}^{2} |\theta|^{\ell}e^{-\theta^2\lVert\vec{\beta}\rVert_2^2/\pi^2}d\theta=\frac{\pi^{\ell+1}}{\lVert\vec{\beta}\rVert_2^{\ell+1}} \int_{-2\lVert\vec{\beta}\rVert_2/\pi}^{2\lVert\vec{\beta}\rVert_2/\pi} |z|^{\ell}e^{-z^2}dz\lesssim_{\ell}\lVert\vec{\beta}\rVert_2^{-(\ell+1)}, \end{align*} $$
$$ \begin{align*} &|\mathbb E[x_{v_{1}}\cdots x_{v_{\ell}}f(\vec{\beta}\cdot\vec{x}-t)]| \\ &\qquad\qquad\le2\int_{-2}^{2}\prod_{j=1}^{\ell}|\theta \beta_{v_j}| \prod_{v\in V\setminus\{v_{1},\ldots,v_{\ell}\}}e^{-(\theta^2/\pi^2)\beta_v^2}\le 2 \int_{-2}^{2}|\theta|^{\ell}e^{-(\theta^{2}/\pi^2)(\lVert\vec{\beta}\rVert_2^2-\ell)}d\theta\\ &\qquad\qquad\lesssim_{\ell}\int_{-2}^{2} |\theta|^{\ell}e^{-\theta^2\lVert\vec{\beta}\rVert_2^2/\pi^2}d\theta=\frac{\pi^{\ell+1}}{\lVert\vec{\beta}\rVert_2^{\ell+1}} \int_{-2\lVert\vec{\beta}\rVert_2/\pi}^{2\lVert\vec{\beta}\rVert_2/\pi} |z|^{\ell}e^{-z^2}dz\lesssim_{\ell}\lVert\vec{\beta}\rVert_2^{-(\ell+1)}, \end{align*} $$
as desired (where in the last step we used that the integral
![]() $\int _{-\infty }^{\infty }|z|^{m}e^{-z^2}dz$
is finite).
$\int _{-\infty }^{\infty }|z|^{m}e^{-z^2}dz$
is finite).
Finally, let us deduce Claim 12.2.
Proof of Claim 12.2
First, note that it suffices to consider the case where the interval
![]() $[a,b]$
has length exactly
$[a,b]$
has length exactly
![]() $(2H+4)n$
. Indeed, in the general case we can cover
$(2H+4)n$
. Indeed, in the general case we can cover
![]() $[a,b]$
with
$[a,b]$
with
![]() $\lceil (b-a)/((2H+4)n)\rceil \lesssim _{C.H} (b-a)/((2H+4)n)$
intervals of length exactly
$\lceil (b-a)/((2H+4)n)\rceil \lesssim _{C.H} (b-a)/((2H+4)n)$
intervals of length exactly
![]() $(2H+4)n$
(here, we used that
$(2H+4)n$
(here, we used that
![]() $b-a\ge \lVert M^*\rVert _{\mathrm {F}}\gtrsim _C n$
by (12.4)). So assume that
$b-a\ge \lVert M^*\rVert _{\mathrm {F}}\gtrsim _C n$
by (12.4)). So assume that
![]() $b-a=(2H+4)n$
and let
$b-a=(2H+4)n$
and let
![]() $s=(a+b)/2$
, then
$s=(a+b)/2$
, then
![]() $[a,b]=[s-(H+2)n,s+(H+2)n]$
.
$[a,b]=[s-(H+2)n,s+(H+2)n]$
.
Using that Q and M are symmetric, recall from Step 5 that
 $$ \begin{align*} \sigma_{\mathrm{shift}}^{2}=\frac{1}{16}\lVert(I-Q)M\vec{\Delta}\rVert_2^2=\frac{1}{16}\lVert(I-Q)MQ\vec{x}\rVert_2^2&=\frac{1}{16}\vec{x}^{\intercal}QM(I-Q)^2MQ\vec{x}\\ &=\frac{n}{16}\vec{x}^{\intercal}\frac{QM(I-Q)^2MQ}{n}\vec{x}. \end{align*} $$
$$ \begin{align*} \sigma_{\mathrm{shift}}^{2}=\frac{1}{16}\lVert(I-Q)M\vec{\Delta}\rVert_2^2=\frac{1}{16}\lVert(I-Q)MQ\vec{x}\rVert_2^2&=\frac{1}{16}\vec{x}^{\intercal}QM(I-Q)^2MQ\vec{x}\\ &=\frac{n}{16}\vec{x}^{\intercal}\frac{QM(I-Q)^2MQ}{n}\vec{x}. \end{align*} $$
Recall that M has entries in
![]() $\{0,1\}$
, and recall the definition of Q in Step 3 (and the fact that multiplying with Q has the effect of averaging values over buckets). This shows that in
$\{0,1\}$
, and recall the definition of Q in Step 3 (and the fact that multiplying with Q has the effect of averaging values over buckets). This shows that in
![]() $QMQ$
and also in
$QMQ$
and also in
![]() $(I-Q)MQ$
(and consequently in
$(I-Q)MQ$
(and consequently in
![]() $(1/n)QM(I-Q)^2MQ$
) all entries have absolute value at most
$(1/n)QM(I-Q)^2MQ$
) all entries have absolute value at most
![]() $1$
.
$1$
.
Furthermore, recall from Step 4 that
![]() $\|Q\vec {y}\|_{\infty }\le (H+2)n$
and
$\|Q\vec {y}\|_{\infty }\le (H+2)n$
and
![]() $\|Q\vec {y}\|_{2}\gtrsim _C n^{3/2}$
. Consider
$\|Q\vec {y}\|_{2}\gtrsim _C n^{3/2}$
. Consider
![]() $\psi $
and f as in the statement of Claim 12.3, and recall from the proof of Lemma 6.1 that
$\psi $
and f as in the statement of Claim 12.3, and recall from the proof of Lemma 6.1 that
![]() for all
for all
![]() $t\in \mathbb {R}$
(more specifically, the function f is given by
$t\in \mathbb {R}$
(more specifically, the function f is given by
![]() $f(t)=(2(\sin t)/t)^2$
for
$f(t)=(2(\sin t)/t)^2$
for
![]() $t\neq 0$
and
$t\neq 0$
and
![]() $f(0)=2^2$
). Also, note that
$f(0)=2^2$
). Also, note that
![]() $E_{\mathrm {shift}(2)}^{2}$
and
$E_{\mathrm {shift}(2)}^{2}$
and
![]() $\sigma _{\mathrm {shift}}^{2}$
are both nonnegative.
$\sigma _{\mathrm {shift}}^{2}$
are both nonnegative.
Now, let
![]() $\vec {\beta }\in \mathbb {R}^V$
be given by
$\vec {\beta }\in \mathbb {R}^V$
be given by
![]() $((H+2)n)^{-1}\cdot \frac {1}{2}Q\vec {y}$
, and note that then
$((H+2)n)^{-1}\cdot \frac {1}{2}Q\vec {y}$
, and note that then
![]() $\lVert \vec {\beta }\rVert _{\infty }\le 1/2<\pi /4$
and
$\lVert \vec {\beta }\rVert _{\infty }\le 1/2<\pi /4$
and
![]() $\lVert \vec {\beta }\rVert _2\gtrsim _{C,H} n^{1/2}$
. Furthermore, let
$\lVert \vec {\beta }\rVert _2\gtrsim _{C,H} n^{1/2}$
. Furthermore, let
![]() $t=((H+2)n)^{-1}s$
, so (recalling that
$t=((H+2)n)^{-1}s$
, so (recalling that
![]() $E_{\mathrm {shift}(1)}=\frac {1}{2}(Q\vec {y})\cdot \vec {x}$
and
$E_{\mathrm {shift}(1)}=\frac {1}{2}(Q\vec {y})\cdot \vec {x}$
and
![]() $[a,b]=[s-(H+2)n,s+(H+2)n]$
) we have
$[a,b]=[s-(H+2)n,s+(H+2)n]$
) we have
![]() $E_{\mathrm {shift}(1)}\in [a,b]$
if and only if
$E_{\mathrm {shift}(1)}\in [a,b]$
if and only if
![]() $\vec {\beta }\cdot \vec {x}-t\in [-1,1]$
. Hence,
$\vec {\beta }\cdot \vec {x}-t\in [-1,1]$
. Hence,

and therefore by Claim 12.3 applied with
![]() $A=QMQ$
and
$A=QMQ$
and
![]() $k=2$
,
$k=2$
,
Similarly, writing
![]() $A=(1/n)QM(I-Q)^2MQ$
and applying Claim 12.3 wih
$A=(1/n)QM(I-Q)^2MQ$
and applying Claim 12.3 wih
![]() $k=1$
, we have
$k=1$
, we have

Summing these two estimates and recalling that
![]() $b-a=(2H+4)n$
now gives the desired result
$b-a=(2H+4)n$
now gives the desired result
13 Switchings for pointwise probability estimates
So far (in Theorem 3.1), we have obtained near-optimal estimates on probabilities of events of the form
![]() $|X-x|\le B$
, for some large constant B. However, in order to prove Theorem 2.1, we need to control the probability that X is exactly equal to x (assuming that
$|X-x|\le B$
, for some large constant B. However, in order to prove Theorem 2.1, we need to control the probability that X is exactly equal to x (assuming that
![]() $e_0$
and the entries of the vector
$e_0$
and the entries of the vector
![]() $\vec {e}$
are integers). Of course, an upper bound on
$\vec {e}$
are integers). Of course, an upper bound on
![]() $\Pr [|X-x|\le B]$
as in Theorem 3.1 implies an upper bound on
$\Pr [|X-x|\le B]$
as in Theorem 3.1 implies an upper bound on
![]() $\Pr [X=x]$
. So it only remains to prove the lower bound in Theorem 2.1.
$\Pr [X=x]$
. So it only remains to prove the lower bound in Theorem 2.1.
In order to deduce the lower bound in Theorem 2.1 from Theorem 3.1, it suffices to show that
![]() $\Pr [X=x]$
does not differ too much from
$\Pr [X=x]$
does not differ too much from
![]() $\Pr [X=x']$
for
$\Pr [X=x']$
for
![]() $x'\in [x-B,x+B]$
. In order to show this, we use the switching method, by which we study the effect of small perturbations to U. For example, in the setting of Theorem 2.1 one can show that for a typical outcome of U there are many pairs of vertices
$x'\in [x-B,x+B]$
. In order to show this, we use the switching method, by which we study the effect of small perturbations to U. For example, in the setting of Theorem 2.1 one can show that for a typical outcome of U there are many pairs of vertices
![]() $(y,z)$
such that
$(y,z)$
such that
![]() $y\in U$
,
$y\in U$
,
![]() $z\notin U$
and
$z\notin U$
and
![]() $|N(z)\cap (U\setminus \{y\})|-|N(y)\cap (U\setminus \{z\})|+e_z-e_y=\ell $
. For such a pair
$|N(z)\cap (U\setminus \{y\})|-|N(y)\cap (U\setminus \{z\})|+e_z-e_y=\ell $
. For such a pair
![]() $(y,z)$
, modifying U by removing y and adding z (a ‘switch’ of y and z) changes X by exactly
$(y,z)$
, modifying U by removing y and adding z (a ‘switch’ of y and z) changes X by exactly
![]() $\ell $
.
$\ell $
.
As discussed in Section 3.5, we introduce an averaged version of the switching method. Roughly speaking, we define random variables that measure the number of ways to switch between two classes and study certain moments of these random variables. We can then make our desired probabilistic conclusions with the Cauchy–Schwarz inequality.
First, we need a lemma providing us with a special set of vertices which we will use for switching operations (the properties in the lemma make it tractable to compute the relevant moments).
For vertices
![]() $v_{1},\ldots ,v_{s}$
in a graph G, let us define
$v_{1},\ldots ,v_{s}$
in a graph G, let us define
to be the set of vertices in
![]() $V(G)\setminus \{v_1,\ldots ,v_s\}$
that are not adjacent to any of the vertices
$V(G)\setminus \{v_1,\ldots ,v_s\}$
that are not adjacent to any of the vertices
![]() $v_1,\ldots ,v_s$
.
$v_1,\ldots ,v_s$
.
Lemma 13.1. For any fixed
![]() $C,H>0$
and
$C,H>0$
and
![]() $D\in \mathbb N$
, there exist
$D\in \mathbb N$
, there exist
![]() $\rho =\rho (C,D)$
with
$\rho =\rho (C,D)$
with
![]() $0<\rho <1$
and
$0<\rho <1$
and
![]() $\delta =\delta (C,D)>0$
with
$\delta =\delta (C,D)>0$
with
![]() $\delta <\rho ^3/3^{D+1}$
such that the following holds for all sufficiently large n. For every C-Ramsey graph G on n vertices and every vector
$\delta <\rho ^3/3^{D+1}$
such that the following holds for all sufficiently large n. For every C-Ramsey graph G on n vertices and every vector
![]() $\vec {e}\in \mathbb {Z}^{V(G)}$
with
$\vec {e}\in \mathbb {Z}^{V(G)}$
with
![]() $0\le e_v\le Hn$
for all
$0\le e_v\le Hn$
for all
![]() $v\in V(G)$
, there exist subsets
$v\in V(G)$
, there exist subsets
![]() $S\subseteq S_0\subseteq V(G)$
with
$S\subseteq S_0\subseteq V(G)$
with
![]() $|S|\geq n^{0.48}$
and
$|S|\geq n^{0.48}$
and
![]() $|S_0|\geq \delta ^{1/\rho }\cdot n$
such that the following properties hold.
$|S_0|\geq \delta ^{1/\rho }\cdot n$
such that the following properties hold.
-
1. The induced subgraph
 $G[S_0]$
is
$G[S_0]$
is
 $(\delta ,\rho )$
-rich (see Definition 4.3).
$(\delta ,\rho )$
-rich (see Definition 4.3). -
2. For any vertices
 $v_{1},\ldots ,v_{s}\in S$
with
$v_{1},\ldots ,v_{s}\in S$
with
 $s\leq D$
, we have
$s\leq D$
, we have
 $|\overline {N}(v_{1},\ldots ,v_{s})\cap S_0|\ge \delta |S_0|$
.
$|\overline {N}(v_{1},\ldots ,v_{s})\cap S_0|\ge \delta |S_0|$
. -
3. For any vertices
 $v,w\in S$
, we have
$v,w\in S$
, we have
 $|\deg _G(v)/2+e_v-\deg _G(w)/2-e_w|\leq \sqrt {n}$
.
$|\deg _G(v)/2+e_v-\deg _G(w)/2-e_w|\leq \sqrt {n}$
.
Remark 13.2. We will apply Lemma 13.1 with
![]() $D=8B+4$
, where
$D=8B+4$
, where
![]() $B=B(C)$
is as in Theorem 3.1. So the size of
$B=B(C)$
is as in Theorem 3.1. So the size of
![]() $S_0$
depends on B. Eventually, we will apply Theorem 3.1 to a Ramsey graph
$S_0$
depends on B. Eventually, we will apply Theorem 3.1 to a Ramsey graph
![]() $G[\overline N]$
, for a certain subset
$G[\overline N]$
, for a certain subset
![]() $\overline N\subseteq S_0$
(with
$\overline N\subseteq S_0$
(with
![]() $U\cap \overline N$
as our random vertex set, conditioning on an outcome of
$U\cap \overline N$
as our random vertex set, conditioning on an outcome of
![]() $U\setminus \overline N$
). Since the proportion of G that
$U\setminus \overline N$
). Since the proportion of G that
![]() $\overline N\subseteq S_0$
occupies depends on D, we will have to apply Theorem 3.1 with
$\overline N\subseteq S_0$
occupies depends on D, we will have to apply Theorem 3.1 with
![]() $A,H$
depending on D (and therefore on B). So, it is crucial that in Theorem 3.1, B does not depend on
$A,H$
depending on D (and therefore on B). So, it is crucial that in Theorem 3.1, B does not depend on
![]() $A,H$
.
$A,H$
.
To prove Lemma 13.1 (specifically, property (2)), we will need a dependent random choice lemma: The following simple yet powerful lemma appears as [Reference Fox and Sudakov46, Lemma 2.1].
Lemma 13.3. Let F be a graph on n vertices with average degree d. Suppose that
![]() $a,s,r\in \mathbb N$
satisfy
$a,s,r\in \mathbb N$
satisfy
 $$\begin{align*}\sup_{t\in\mathbb N}\left(\frac{d^{t}}{n^{t-1}}-\binom{n}{r}\cdot \left(\frac{s}{n}\right)^{t}\right)\ge a. \end{align*}$$
$$\begin{align*}\sup_{t\in\mathbb N}\left(\frac{d^{t}}{n^{t-1}}-\binom{n}{r}\cdot \left(\frac{s}{n}\right)^{t}\right)\ge a. \end{align*}$$
Then, F has a subset W of at least a vertices such that every r vertices in W have at least s common neighbors in F.
Proof of Lemma 13.1
Let
![]() $\varepsilon =\varepsilon (2C)$
be as in Theorem 4.1, so for sufficiently large m every
$\varepsilon =\varepsilon (2C)$
be as in Theorem 4.1, so for sufficiently large m every
![]() $2C$
-Ramsey graph on m vertices has average degree at least
$2C$
-Ramsey graph on m vertices has average degree at least
![]() $\varepsilon m$
. Let
$\varepsilon m$
. Let
![]() $\rho =\rho (C,1/5)>0$
be as in Lemma 4.4. Let
$\rho =\rho (C,1/5)>0$
be as in Lemma 4.4. Let
![]() $\delta =\delta (C,D)>0$
be sufficiently small such that
$\delta =\delta (C,D)>0$
be sufficiently small such that
![]() $\delta <\rho ^3/3^{D+1}$
and for all sufficiently large m (in terms of C and D) we have
$\delta <\rho ^3/3^{D+1}$
and for all sufficiently large m (in terms of C and D) we have
 $$\begin{align*}\sup_{t\in\mathbb N}\left(\varepsilon^{t}m-\binom{m}{D}\delta^{t}\right)\ge m^{0.99}. \end{align*}$$
$$\begin{align*}\sup_{t\in\mathbb N}\left(\varepsilon^{t}m-\binom{m}{D}\delta^{t}\right)\ge m^{0.99}. \end{align*}$$
To see that this is possible, consider
![]() $t=\eta \log m$
for some small
$t=\eta \log m$
for some small
![]() $\eta $
(in terms of
$\eta $
(in terms of
![]() $\varepsilon $
), and let
$\varepsilon $
), and let
![]() $\delta $
be small in terms of
$\delta $
be small in terms of
![]() $\eta $
and D.
$\eta $
and D.
By Lemma 4.4, we can find a
![]() $(\delta ,\rho )$
-rich induced subgraph
$(\delta ,\rho )$
-rich induced subgraph
![]() $G[S_{0}]$
of size
$G[S_{0}]$
of size
![]() $|S_0|\ge \delta ^{1/\rho }\cdot n$
.
$|S_0|\ge \delta ^{1/\rho }\cdot n$
.
Since
![]() $|S_0|\geq \delta ^{1/\rho }\cdot n\ge \sqrt {n}$
, the graph
$|S_0|\geq \delta ^{1/\rho }\cdot n\ge \sqrt {n}$
, the graph
![]() $G[S_0]$
is
$G[S_0]$
is
![]() $2C$
-Ramsey. Let
$2C$
-Ramsey. Let
![]() $\overline G[S_0]$
be the complement of this graph so that
$\overline G[S_0]$
be the complement of this graph so that
![]() $\overline G[S_0]$
is also a
$\overline G[S_0]$
is also a
![]() $2C$
-Ramsey graph and therefore has average degree at least
$2C$
-Ramsey graph and therefore has average degree at least
![]() $\varepsilon |S_{0}|$
. By Lemma 13.3 and the choice of
$\varepsilon |S_{0}|$
. By Lemma 13.3 and the choice of
![]() $\delta $
, the graph
$\delta $
, the graph
![]() $\overline G[S_0]$
contains a set
$\overline G[S_0]$
contains a set
![]() $S'$
of
$S'$
of
![]() $|S'|\geq |S_{0}|^{0.99}\ge 2(H+1)n^{0.98}$
vertices such that every D vertices in
$|S'|\geq |S_{0}|^{0.99}\ge 2(H+1)n^{0.98}$
vertices such that every D vertices in
![]() $S'$
have at least
$S'$
have at least
![]() $\delta |S_{0}|$
common neighbors in
$\delta |S_{0}|$
common neighbors in
![]() $\overline G[S_0]$
. This means that for any
$\overline G[S_0]$
. This means that for any
![]() $s\le D$
and any
$s\le D$
and any
![]() $v_{1},\ldots ,v_{s}\in S'$
, we have
$v_{1},\ldots ,v_{s}\in S'$
, we have
![]() $|\overline {N}(v_{1},\ldots ,v_{s})\cap S_0|\ge \delta |S_{0}|$
, so (2) holds for any subset
$|\overline {N}(v_{1},\ldots ,v_{s})\cap S_0|\ge \delta |S_{0}|$
, so (2) holds for any subset
![]() $S\subseteq S'$
.
$S\subseteq S'$
.
Finally, note that
![]() $\deg _G(v)/2+e_v\in [0,(H+1)n]$
for all
$\deg _G(v)/2+e_v\in [0,(H+1)n]$
for all
![]() $v\in S'$
, and consider a partition of the interval
$v\in S'$
, and consider a partition of the interval
![]() $[0,(H+1)n]$
into
$[0,(H+1)n]$
into
![]() $\lfloor 2(H+1) \sqrt {n}\rfloor $
subintervals of length
$\lfloor 2(H+1) \sqrt {n}\rfloor $
subintervals of length
![]() $ (H+1)n/\lfloor 2(H+1) \sqrt {n}\rfloor \leq \sqrt {n}$
. By the pigeonhole principle, there exists a set
$ (H+1)n/\lfloor 2(H+1) \sqrt {n}\rfloor \leq \sqrt {n}$
. By the pigeonhole principle, there exists a set
![]() $S\subseteq S'$
of at least
$S\subseteq S'$
of at least
![]() $ 2(H+1)n^{0.98}/\lfloor 2(H+1) \sqrt {n}\rfloor \ge n^{0.48}$
vertices v whose associated values
$ 2(H+1)n^{0.98}/\lfloor 2(H+1) \sqrt {n}\rfloor \ge n^{0.48}$
vertices v whose associated values
![]() $\deg _G(v)/2+e_v$
lie in the same subinterval. Then (3) holds.
$\deg _G(v)/2+e_v$
lie in the same subinterval. Then (3) holds.
As foreshadowed earlier, the next lemma estimates moments of certain random variables that measure the number of ways to switch between certain choices of the set U. The proof of this lemma relies on Theorem 3.1.
Lemma 13.4. Fix
![]() $C,H,A>0$
, let
$C,H,A>0$
, let
![]() $B=B(2C)$
be as in Theorem 3.1 and define
$B=B(2C)$
be as in Theorem 3.1 and define
![]() $D=D(C)=8B+4$
. Consider a C-Ramsey graph G on n vertices and a vector
$D=D(C)=8B+4$
. Consider a C-Ramsey graph G on n vertices and a vector
![]() $\vec {e}\in \mathbb {Z}^{V(G)}$
with
$\vec {e}\in \mathbb {Z}^{V(G)}$
with
![]() $0\le e_v\le Hn$
for all
$0\le e_v\le Hn$
for all
![]() $v\in V(G)$
. Let
$v\in V(G)$
. Let
![]() $S\subseteq S_0\subseteq V(G)$
,
$S\subseteq S_0\subseteq V(G)$
,
![]() $\rho =\rho (C,D)>0$
and
$\rho =\rho (C,D)>0$
and
![]() $\delta =\delta (C,D)>0$
be as in Lemma 13.1, and define
$\delta =\delta (C,D)>0$
be as in Lemma 13.1, and define
Consider a random vertex subset
![]() $U\subseteq V(G)$
obtained by including each vertex with probability
$U\subseteq V(G)$
obtained by including each vertex with probability
![]() $1/2$
independently, and let
$1/2$
independently, and let
![]() $X=e(G[U])+\sum _{u\in U}e_u$
. For
$X=e(G[U])+\sum _{u\in U}e_u$
. For
![]() $\ell =-B,\ldots ,B$
, let
$\ell =-B,\ldots ,B$
, let
![]() $Y_{\ell }$
be the number of vertex pairs
$Y_{\ell }$
be the number of vertex pairs
![]() $(y,z)\in T$
with
$(y,z)\in T$
with
![]() $y\in U$
and
$y\in U$
and
![]() $z\notin U$
such that
$z\notin U$
such that
![]() $(|N(z)\cap (U\setminus \{y\})|+e_z)-(|N(y)\cap (U\setminus \{z\})|+e_y)=\ell $
. For
$(|N(z)\cap (U\setminus \{y\})|+e_z)-(|N(y)\cap (U\setminus \{z\})|+e_y)=\ell $
. For
![]() $x\in \mathbb Z$
, let
$x\in \mathbb Z$
, let
![]() $Z_{x-B,x+B}\in \{0,1\}$
be the indicator random variable for the event that
$Z_{x-B,x+B}\in \{0,1\}$
be the indicator random variable for the event that
![]() $x-B\le X\le x+B$
.
$x-B\le X\le x+B$
.
Then, for any
![]() $x\in \mathbb Z$
satisfying
$x\in \mathbb Z$
satisfying
![]() $|x-\mathbb EX|\le An^{3/2}$
and any
$|x-\mathbb EX|\le An^{3/2}$
and any
![]() $a_{-B},\ldots ,a_{B}\in \{0,1,2\}$
, we have
$a_{-B},\ldots ,a_{B}\in \{0,1,2\}$
, we have
We defer the proof of Lemma 13.4 (using Theorem 3.1) until the end of the section, first showing how it can be used to prove Theorem 2.1. This argument requires the set T in Lemma 13.4 to be nonempty, which is implied by the following lemma.
Lemma 13.5. The set T defined in Lemma 13.4 has size
![]() $|T|\geq |S|^2/2\geq n^{0.96}/2$
.
$|T|\geq |S|^2/2\geq n^{0.96}/2$
.
Proof. Recall that the set
![]() $S\subseteq S_0$
has size
$S\subseteq S_0$
has size
![]() $|S|\geq n^{0.48}$
and that
$|S|\geq n^{0.48}$
and that
![]() $G[S_0]$
is
$G[S_0]$
is
![]() $(\delta ,\rho )$
-rich, where
$(\delta ,\rho )$
-rich, where
![]() $\delta <\rho ^3/3^{D+1}< \rho $
is as in Lemma 13.1. We first claim that at least
$\delta <\rho ^3/3^{D+1}< \rho $
is as in Lemma 13.1. We first claim that at least
![]() $(3/4)\cdot |S|^2$
pairs
$(3/4)\cdot |S|^2$
pairs
![]() $(y,z)\in S^{2}$
satisfy the first condition
$(y,z)\in S^{2}$
satisfy the first condition
![]() $|(N(z)\setminus N(y))\cap S_0|\geq \rho ^2 |S_0|$
in the definition of T. Indeed, by Definition 4.3, all but at most
$|(N(z)\setminus N(y))\cap S_0|\geq \rho ^2 |S_0|$
in the definition of T. Indeed, by Definition 4.3, all but at most
![]() $n^{1/5}$
vertices
$n^{1/5}$
vertices
![]() $z\in S_0$
satisfy
$z\in S_0$
satisfy
![]() $|N(z)\cap S_0|\geq \rho |S_0|$
. Hence,
$|N(z)\cap S_0|\geq \rho |S_0|$
. Hence,
![]() $|N(z)\cap S_0|\geq \rho |S_0|$
for at least
$|N(z)\cap S_0|\geq \rho |S_0|$
for at least
![]() $|S|-n^{1/5}$
vertices
$|S|-n^{1/5}$
vertices
![]() $z\in S$
. Furthermore, for each such
$z\in S$
. Furthermore, for each such
![]() $z\in S$
we have
$z\in S$
we have
![]() $|(N(z)\setminus N(y))\cap S_0|=|(N(z)\cap S_0)\setminus N(y)|\geq \rho \cdot |N(z)\cap S_0|\geq \rho ^2|S_0|$
for all but at most
$|(N(z)\setminus N(y))\cap S_0|=|(N(z)\cap S_0)\setminus N(y)|\geq \rho \cdot |N(z)\cap S_0|\geq \rho ^2|S_0|$
for all but at most
![]() $n^{1/5}$
vertices
$n^{1/5}$
vertices
![]() $y\in S_0$
and in particular for at least
$y\in S_0$
and in particular for at least
![]() $|S|-n^{1/5}$
vertices
$|S|-n^{1/5}$
vertices
![]() $y\in S$
. Thus, there are at least
$y\in S$
. Thus, there are at least
![]() $(|S|-n^{1/5})^2\geq (3/4)\cdot |S|^2$
pairs
$(|S|-n^{1/5})^2\geq (3/4)\cdot |S|^2$
pairs
![]() $(y,z)\in S^2$
satisfying
$(y,z)\in S^2$
satisfying
![]() $|(N(z)\setminus N(y))\cap S_0|\geq \rho ^2 |S_0|$
. Analogously, at least
$|(N(z)\setminus N(y))\cap S_0|\geq \rho ^2 |S_0|$
. Analogously, at least
![]() $(3/4)\cdot |S|^2$
pairs
$(3/4)\cdot |S|^2$
pairs
![]() $(y,z)\in S^{2}$
satisfy the second condition
$(y,z)\in S^{2}$
satisfy the second condition
![]() $|(N(y)\setminus N(z))\cap S_0|\geq \rho ^2 |S_0|$
in the definition of T. This means that the number of pairs
$|(N(y)\setminus N(z))\cap S_0|\geq \rho ^2 |S_0|$
in the definition of T. This means that the number of pairs
![]() $(y,z)\in S^2$
satisfying both conditions is at least
$(y,z)\in S^2$
satisfying both conditions is at least
![]() $|S|^2-2(|S|^2-(3/4)\cdot |S|^2)=|S|^2/2$
and hence
$|S|^2-2(|S|^2-(3/4)\cdot |S|^2)=|S|^2/2$
and hence
![]() $|T|\geq |S|^2/2\geq n^{0.96}/2$
.
$|T|\geq |S|^2/2\geq n^{0.96}/2$
.
Now, we are ready to deduce Theorem 2.1 from Lemma 13.4.
Proof of Theorem 2.1
Consider a C-Ramsey graph G, a random subset
![]() $U\subseteq V(G)$
and
$U\subseteq V(G)$
and
![]() $X=e(G[U])+\sum _{v\in U}e_v+e_0$
as in Theorem 2.1, and consider the setup of Lemma 13.4. Note that the upper bound in Theorem 2.1 follows immediately from the upper bound in Theorem 3.1, so it only remains to prove the lower bound.
$X=e(G[U])+\sum _{v\in U}e_v+e_0$
as in Theorem 2.1, and consider the setup of Lemma 13.4. Note that the upper bound in Theorem 2.1 follows immediately from the upper bound in Theorem 3.1, so it only remains to prove the lower bound.
For
![]() $x\in \mathbb Z$
, let
$x\in \mathbb Z$
, let
![]() $Z_{x}$
be the indicator random variable for the event that
$Z_{x}$
be the indicator random variable for the event that
![]() $X=x$
. Note that for all
$X=x$
. Note that for all
![]() $x\in \mathbb Z$
and
$x\in \mathbb Z$
and
![]() $\ell =-B,\ldots ,B$
we have
$\ell =-B,\ldots ,B$
we have
![]() $\mathbb E[Y_{-\ell }Z_{x+\ell }]=\mathbb E[Y_{\ell }Z_{x}]$
. Indeed, if
$\mathbb E[Y_{-\ell }Z_{x+\ell }]=\mathbb E[Y_{\ell }Z_{x}]$
. Indeed, if
![]() $X=e(G[U])+\sum _{u\in U}e_u+e_0=x+\ell $
, then
$X=e(G[U])+\sum _{u\in U}e_u+e_0=x+\ell $
, then
![]() $Y_{-\ell }$
is the number of ways to perform a ‘switch’ of two vertices
$Y_{-\ell }$
is the number of ways to perform a ‘switch’ of two vertices
![]() $y\in U$
,
$y\in U$
,
![]() $z\notin U$
with
$z\notin U$
with
![]() $(y,z)\in T$
, to obtain a vertex subset
$(y,z)\in T$
, to obtain a vertex subset
![]() $U'=(U\setminus \{y\})\cup \{z\}$
with
$U'=(U\setminus \{y\})\cup \{z\}$
with
![]() $e(G[U'])+\sum _{v\in U'}e_v+e_0=x$
. Conversely, if
$e(G[U'])+\sum _{v\in U'}e_v+e_0=x$
. Conversely, if
![]() $X=e(G[U])+\sum _{v\in U}e_v+e_0=x$
, then
$X=e(G[U])+\sum _{v\in U}e_v+e_0=x$
, then
![]() $Y_{\ell }$
is the number of ways to perform such a switch ‘in reverse’ to obtain a vertex subset
$Y_{\ell }$
is the number of ways to perform such a switch ‘in reverse’ to obtain a vertex subset
![]() $U'$
with
$U'$
with
![]() $e(G[U'])+\sum _{v\in U'}e_v+e_0=x+\ell $
. So,
$e(G[U'])+\sum _{v\in U'}e_v+e_0=x+\ell $
. So,
![]() $2^{n}\mathbb E[Y_{-\ell }Z_{x+\ell }]$
and
$2^{n}\mathbb E[Y_{-\ell }Z_{x+\ell }]$
and
![]() $2^{n}\mathbb E[Y_{\ell }Z_{x}]$
both describe the total number of ways to switch in this way between an outcome of U with
$2^{n}\mathbb E[Y_{\ell }Z_{x}]$
both describe the total number of ways to switch in this way between an outcome of U with
![]() $X=x+\ell $
and an outcome with
$X=x+\ell $
and an outcome with
![]() $X=x$
.
$X=x$
.
Now, for every
![]() $x\in \mathbb Z$
with
$x\in \mathbb Z$
with
![]() $|x-\mathbb E X|\le An^{3/2}$
there is some
$|x-\mathbb E X|\le An^{3/2}$
there is some
![]() $\ell \in \{-B,\ldots ,B\}$
such that
$\ell \in \{-B,\ldots ,B\}$
such that
 $$ \begin{align*} \mathbb E[Y_{-B}\cdots Y_{B}Z_{x+\ell}]&\ge\frac{1}{2B+1}\sum_{\ell'=-B}^B\mathbb E[Y_{-B}\cdots Y_{B}Z_{x+\ell'}]\\ &=\frac{1}{2B+1} \mathbb E[Y_{-B}\cdots Y_{B}Z_{x-B,x+B}]\gtrsim_{C,H,A}\frac{(|T|/\sqrt{n})^{2B+1}}{n^{3/2}},\end{align*} $$
$$ \begin{align*} \mathbb E[Y_{-B}\cdots Y_{B}Z_{x+\ell}]&\ge\frac{1}{2B+1}\sum_{\ell'=-B}^B\mathbb E[Y_{-B}\cdots Y_{B}Z_{x+\ell'}]\\ &=\frac{1}{2B+1} \mathbb E[Y_{-B}\cdots Y_{B}Z_{x-B,x+B}]\gtrsim_{C,H,A}\frac{(|T|/\sqrt{n})^{2B+1}}{n^{3/2}},\end{align*} $$
where the last step is by Lemma 13.4. For this
![]() $\ell $
, the Cauchy–Schwarz inequality, together with Lemma 13.4 and the fact that
$\ell $
, the Cauchy–Schwarz inequality, together with Lemma 13.4 and the fact that
![]() $Z_{x+\ell }\le Z_{x-B,x+B}$
, implies that
$Z_{x+\ell }\le Z_{x-B,x+B}$
, implies that
 $$ \begin{align*}\mathbb E[Y_{\ell}Z_{x}]=\mathbb E[Y_{-\ell}Z_{x+\ell}]&\ge\frac{(\mathbb E[Y_{-B}\cdots Y_{B}Z_{x+\ell}])^{2}}{\mathbb E[Y_{-B}^{2}\cdots Y_{-\ell-1}^{2}Y_{-\ell}Y_{-\ell+1}^{2}\cdots Y_{B}^{2}Z_{x+\ell}]}\\ &\gtrsim_{C,H,A}\frac{(|T|/\sqrt{n})^{4B+2}/n^{3}}{(|T|/\sqrt{n})^{4B+1}/n^{3/2}}=\frac{|T|/\sqrt{n}}{n^{3/2}}. \end{align*} $$
$$ \begin{align*}\mathbb E[Y_{\ell}Z_{x}]=\mathbb E[Y_{-\ell}Z_{x+\ell}]&\ge\frac{(\mathbb E[Y_{-B}\cdots Y_{B}Z_{x+\ell}])^{2}}{\mathbb E[Y_{-B}^{2}\cdots Y_{-\ell-1}^{2}Y_{-\ell}Y_{-\ell+1}^{2}\cdots Y_{B}^{2}Z_{x+\ell}]}\\ &\gtrsim_{C,H,A}\frac{(|T|/\sqrt{n})^{4B+2}/n^{3}}{(|T|/\sqrt{n})^{4B+1}/n^{3/2}}=\frac{|T|/\sqrt{n}}{n^{3/2}}. \end{align*} $$
Finally, we use the Cauchy–Schwarz inequality and Lemma 13.4 once more (noting that
![]() $Z_{x}\le Z_{x-B,x+B}$
) to conclude that
$Z_{x}\le Z_{x-B,x+B}$
) to conclude that
 $$\begin{align*}\Pr[X=x]=\mathbb E Z_{x}\ge\frac{(\mathbb E[Y_{\ell}Z_{x}])^{2}}{\mathbb E[Y_{\ell}^{2}Z_{x}]}\gtrsim_{C,H,A} \frac{(|T|/\sqrt{n})^{2}/n^{3}}{(|T|/\sqrt{n})^{2}/n^{3/2}}=\frac{1}{n^{3/2}}.\\[-47pt] \end{align*}$$
$$\begin{align*}\Pr[X=x]=\mathbb E Z_{x}\ge\frac{(\mathbb E[Y_{\ell}Z_{x}])^{2}}{\mathbb E[Y_{\ell}^{2}Z_{x}]}\gtrsim_{C,H,A} \frac{(|T|/\sqrt{n})^{2}/n^{3}}{(|T|/\sqrt{n})^{2}/n^{3/2}}=\frac{1}{n^{3/2}}.\\[-47pt] \end{align*}$$
It now remains to prove the moment estimates in Lemma 13.4. We will write the desired moments as a combinatorial sum of probabilities; for various tuples of pairs of vertices
![]() $(y,z)$
, we then need to control the joint probability that
$(y,z)$
, we then need to control the joint probability that
![]() $X=e(G[U])+\sum _{u\in U}e_u$
lies in a certain interval and that U contains a specified number of vertices from the neighborhoods of the various y and z. The next lemma gives a lower bound for certain probabilities of this form. Slightly more precisely, it allows us to specify the intersection sizes of U in with given disjoint vertex subsets
$X=e(G[U])+\sum _{u\in U}e_u$
lies in a certain interval and that U contains a specified number of vertices from the neighborhoods of the various y and z. The next lemma gives a lower bound for certain probabilities of this form. Slightly more precisely, it allows us to specify the intersection sizes of U in with given disjoint vertex subsets
![]() $W_{1},\ldots ,W_{s}$
. When applying this lemma in the proof of Lemma 13.4, we will take
$W_{1},\ldots ,W_{s}$
. When applying this lemma in the proof of Lemma 13.4, we will take
![]() $s=a_{-B}+\cdots +a_B$
, and given s pairs of vertices
$s=a_{-B}+\cdots +a_B$
, and given s pairs of vertices
![]() $(y_1,z_1),\ldots ,(y_s,z_s)\in T$
, we will take
$(y_1,z_1),\ldots ,(y_s,z_s)\in T$
, we will take
![]() $W_1,\ldots ,W_s$
to be certain regions of the Venn diagram given by the neighborhoods of
$W_1,\ldots ,W_s$
to be certain regions of the Venn diagram given by the neighborhoods of
![]() $y_1,z_1,\ldots ,y_s,z_s$
. We can then use the intersection sizes of U with
$y_1,z_1,\ldots ,y_s,z_s$
. We can then use the intersection sizes of U with
![]() $W_1,\ldots ,W_s$
to control the events that the s-tuple of pairs
$W_1,\ldots ,W_s$
to control the events that the s-tuple of pairs
![]() $(y_1,z_1),\ldots ,(y_s,z_s)$
contributes to
$(y_1,z_1),\ldots ,(y_s,z_s)$
contributes to
![]() $Y_{-B}^{a_{-B}}\cdots Y_{B}^{a_{B}}Z_{x-B,x+B}$
. For this argument, we will, however, need to condition on the outcome of U outside these special regions of the Venn diagram. This conditioning affects the linear terms and constant terms in our random variable X, so we use the variables
$Y_{-B}^{a_{-B}}\cdots Y_{B}^{a_{B}}Z_{x-B,x+B}$
. For this argument, we will, however, need to condition on the outcome of U outside these special regions of the Venn diagram. This conditioning affects the linear terms and constant terms in our random variable X, so we use the variables
![]() $f_v$
and
$f_v$
and
![]() $f_0$
in the lemma statement below (when applying the lemma, we take
$f_0$
in the lemma statement below (when applying the lemma, we take
![]() $f_v$
and
$f_v$
and
![]() $f_0$
to be the terms obtained from
$f_0$
to be the terms obtained from
![]() $e_v$
and
$e_v$
and
![]() $e_0$
after accounting for this conditioning).
$e_0$
after accounting for this conditioning).
Lemma 13.6. Let
![]() $\delta '>0$
and
$\delta '>0$
and
![]() $R\geq 1$
, and consider an n-vertex graph G, a real number
$R\geq 1$
, and consider an n-vertex graph G, a real number
![]() $f_0$
, and a sequence
$f_0$
, and a sequence
![]() $\vec {f}\in \mathbb {R}^{V(G)}$
with
$\vec {f}\in \mathbb {R}^{V(G)}$
with
![]() $|f_{v}|\le R n$
for each
$|f_{v}|\le R n$
for each
![]() $v\in V(G)$
. Let
$v\in V(G)$
. Let
![]() $U\subseteq V(G)$
be a vertex subset obtained by including each vertex with probability
$U\subseteq V(G)$
be a vertex subset obtained by including each vertex with probability
![]() $1/2$
independently, and let
$1/2$
independently, and let
![]() $X=e(G[U])+\sum _{v\in U}f_{v}+f_0$
. Then the following hold.
$X=e(G[U])+\sum _{v\in U}f_{v}+f_0$
. Then the following hold.
-
1.
 $\operatorname {Var}[X]\leq R^2n^3$
.
$\operatorname {Var}[X]\leq R^2n^3$
. -
2. For any
 $s\leq R$
and any disjoint subsets
$s\leq R$
and any disjoint subsets
 $W_{1},\ldots ,W_{s}\subseteq V(G)$
, each of size at least
$W_{1},\ldots ,W_{s}\subseteq V(G)$
, each of size at least
 $\delta ' n$
, and any
$\delta ' n$
, and any
 $w_{1},\ldots ,w_{s}\in \mathbb Z$
satisfying
$w_{1},\ldots ,w_{s}\in \mathbb Z$
satisfying
 $\big |w_{i}-|W_{i}|/2\big |\le R\sqrt {n}$
for
$\big |w_{i}-|W_{i}|/2\big |\le R\sqrt {n}$
for
 $i=1,\ldots ,s$
, we have
$i=1,\ldots ,s$
, we have  $$\begin{align*}\Pr\left[|X-\mathbb E X|\leq 6R^2n^{3/2}\text{ and }|U\cap W_i|=w_i\text{ for }i=1,\ldots,s\right]\gtrsim_{\delta', R} n^{-s/2}.\end{align*}$$
$$\begin{align*}\Pr\left[|X-\mathbb E X|\leq 6R^2n^{3/2}\text{ and }|U\cap W_i|=w_i\text{ for }i=1,\ldots,s\right]\gtrsim_{\delta', R} n^{-s/2}.\end{align*}$$
Proof. For (1), the expression for X in (3.1) and the formula in (4.5) show that
 $$\begin{align*}\operatorname{Var}[X]=\frac{1}{4}\sum_{v\in V(G)}\left(f_v+\frac{1}{2}\deg(v)\right)^2+\frac{1}{16}e(G)\leq R^2n^3.\end{align*}$$
$$\begin{align*}\operatorname{Var}[X]=\frac{1}{4}\sum_{v\in V(G)}\left(f_v+\frac{1}{2}\deg(v)\right)^2+\frac{1}{16}e(G)\leq R^2n^3.\end{align*}$$
Let
![]() $E=\mathbb {E}X$
, and note that for each
$E=\mathbb {E}X$
, and note that for each
![]() $i=1,\ldots ,s$
we have
$i=1,\ldots ,s$
we have
 $$\begin{align*}\Pr[|U\cap W_i|=w_i]=\binom{|W_i|}{w_i}^{-1}\asymp_{\delta',R} n^{-1/2}.\end{align*}$$
$$\begin{align*}\Pr[|U\cap W_i|=w_i]=\binom{|W_i|}{w_i}^{-1}\asymp_{\delta',R} n^{-1/2}.\end{align*}$$
and these events are independent for all i. Thus, in order to establish (2), it suffices to show that when conditioning on
![]() $|U\cap W_i|=w_i$
for
$|U\cap W_i|=w_i$
for
![]() $i=1,\ldots ,s$
, we have
$i=1,\ldots ,s$
, we have
![]() $|X-E|\leq 6R^2n^{3/2}$
with probability at least
$|X-E|\leq 6R^2n^{3/2}$
with probability at least
![]() $1/2$
.
$1/2$
.
Also, note that the value of X changes by at most
![]() $(R+1)n$
when adding or deleting a vertex of U. We can sample a uniformly random subset
$(R+1)n$
when adding or deleting a vertex of U. We can sample a uniformly random subset
![]() $U\subseteq V(G)$
conditioned on
$U\subseteq V(G)$
conditioned on
![]() $|U\cap W_i|=w_i$
for
$|U\cap W_i|=w_i$
for
![]() $i=1,\ldots ,s$
by the following procedure. First, sample a uniformly random subset
$i=1,\ldots ,s$
by the following procedure. First, sample a uniformly random subset
![]() $U'\subseteq V(G)$
, and then construct U from
$U'\subseteq V(G)$
, and then construct U from
![]() $U'$
by deleting
$U'$
by deleting
![]() $|U'\cap W_i|-w_i$
uniformly randomly chosen vertices from
$|U'\cap W_i|-w_i$
uniformly randomly chosen vertices from
![]() $U'\cap W_i$
(if
$U'\cap W_i$
(if
![]() $|U'\cap W_i|\ge w_i$
) or adding
$|U'\cap W_i|\ge w_i$
) or adding
![]() $w_i-|U'\cap W_i|$
randomly chosen vertices from
$w_i-|U'\cap W_i|$
randomly chosen vertices from
![]() $W_i\setminus U'$
to
$W_i\setminus U'$
to
![]() $U'$
(if
$U'$
(if
![]() $|U'\cap W_i|<w_i$
) for each
$|U'\cap W_i|<w_i$
) for each
![]() $i=1,\ldots ,s$
. With probability at least
$i=1,\ldots ,s$
. With probability at least
![]() $1/2$
the value
$1/2$
the value
![]() $X'=e(G[U'])+\sum _{v\in U'}f_{v}+f_0$
satisfies
$X'=e(G[U'])+\sum _{v\in U'}f_{v}+f_0$
satisfies
![]() $|X'-E|\leq 2Rn^{3/2}$
and we have
$|X'-E|\leq 2Rn^{3/2}$
and we have
![]() $||U'\cap W_i|-|W_i|/2|\leq s\sqrt {n}$
for
$||U'\cap W_i|-|W_i|/2|\leq s\sqrt {n}$
for
![]() $i=1,\ldots ,n$
(by Chebyshev’s inequality using
$i=1,\ldots ,n$
(by Chebyshev’s inequality using
![]() $\operatorname {Var}[X']\leq R^2n^3$
and
$\operatorname {Var}[X']\leq R^2n^3$
and
![]() $\operatorname {Var}[|U'\cap W_i|]\leq n/4$
). Whenever this is the case, we have
$\operatorname {Var}[|U'\cap W_i|]\leq n/4$
). Whenever this is the case, we have
![]() $\big ||U'\cap W_i|-w_i\big |\leq 2R\sqrt {n}$
for
$\big ||U'\cap W_i|-w_i\big |\leq 2R\sqrt {n}$
for
![]() $i=1,\ldots ,s$
, implying
$i=1,\ldots ,s$
, implying
![]() $|X-X'|\leq 4R^2n^{3/2}$
and thus
$|X-X'|\leq 4R^2n^{3/2}$
and thus
![]() $|X-E|\leq 4R^2n^{3/2}+2Rn^{3/2}\leq 6R^2n^{3/2}$
, as desired.
$|X-E|\leq 4R^2n^{3/2}+2Rn^{3/2}\leq 6R^2n^{3/2}$
, as desired.
The proof of Lemma 13.4 involves the consideration of tuples
![]() $((y_1,z_1),\ldots ,(y_s,z_s))\in T^s$
and studies the probability that each
$((y_1,z_1),\ldots ,(y_s,z_s))\in T^s$
and studies the probability that each
![]() $(y_i,z_i)$
contributes to some specified
$(y_i,z_i)$
contributes to some specified
![]() $Y_{\ell _i}$
. So, we will need to establish various properties of the tuples
$Y_{\ell _i}$
. So, we will need to establish various properties of the tuples
![]() $((y_1,z_1),\ldots ,(y_s,z_s))\in T^s$
. In particular, the properties in the following definition will be used in our proof of the upper bound in Lemma 13.4. In this definition, and for the rest of this section, we write
$((y_1,z_1),\ldots ,(y_s,z_s))\in T^s$
. In particular, the properties in the following definition will be used in our proof of the upper bound in Lemma 13.4. In this definition, and for the rest of this section, we write
![]() $\vec 1_A$
for the characteristic vector of a set A (with
$\vec 1_A$
for the characteristic vector of a set A (with
![]() $(\vec 1_A)_i=1$
if
$(\vec 1_A)_i=1$
if
![]() $i\in A$
, and
$i\in A$
, and
![]() $(\vec 1_A)_i=0$
otherwise).Footnote 11
$(\vec 1_A)_i=0$
otherwise).Footnote 11
Definition 13.7. Fix
![]() $C>0$
and let
$C>0$
and let
![]() $\rho =\rho (C)>0$
and
$\rho =\rho (C)>0$
and
![]() $\delta =\delta (C)>0$
be as in Lemma 13.4. For a C-Ramsey graph G on n vertices and vertex pairs
$\delta =\delta (C)>0$
be as in Lemma 13.4. For a C-Ramsey graph G on n vertices and vertex pairs
![]() $(y_1,z_1),\ldots ,(y_s,z_s)\in V(G)^2$
, let us define
$(y_1,z_1),\ldots ,(y_s,z_s)\in V(G)^2$
, let us define
![]() $M(y_1,z_1,\ldots ,y_s,z_s)$
to be the
$M(y_1,z_1,\ldots ,y_s,z_s)$
to be the
![]() $s\times n$
matrix (with rows indexed by
$s\times n$
matrix (with rows indexed by
![]() $1,\ldots ,s$
and columns indexed by
$1,\ldots ,s$
and columns indexed by
![]() $V(G)$
) with entries in
$V(G)$
) with entries in
![]() $\{-1,0,1\}$
such that for
$\{-1,0,1\}$
such that for
![]() $i=1,\ldots ,s$
the i-th row of
$i=1,\ldots ,s$
the i-th row of
![]() $M(y_1,z_1,\ldots ,y_s,z_s)$
is the difference of characteristic vectors
$M(y_1,z_1,\ldots ,y_s,z_s)$
is the difference of characteristic vectors
![]() $\vec {1}_{N(z_i)\setminus \{y_i\}}-\vec {1}_{N(y_i)\setminus \{z_i\}}\in \mathbb {R}^{V(G)}$
. We say that
$\vec {1}_{N(z_i)\setminus \{y_i\}}-\vec {1}_{N(y_i)\setminus \{z_i\}}\in \mathbb {R}^{V(G)}$
. We say that
![]() $((y_1,z_1),\ldots ,(y_s,z_s))$
is k-degenerate for some
$((y_1,z_1),\ldots ,(y_s,z_s))$
is k-degenerate for some
![]() $k\in \{0,\ldots ,s\}$
if it is possible to delete at most
$k\in \{0,\ldots ,s\}$
if it is possible to delete at most
![]() $\delta ^{3/\rho }\cdot n$
columns from the matrix
$\delta ^{3/\rho }\cdot n$
columns from the matrix
![]() $M(y_1,z_1,\ldots ,y_s,z_s)$
and obtain a matrix of rank at most
$M(y_1,z_1,\ldots ,y_s,z_s)$
and obtain a matrix of rank at most
![]() $s-k$
. We furthermore define the degeneracy of
$s-k$
. We furthermore define the degeneracy of
![]() $((y_1,z_1),\ldots ,(y_s,z_s))$
to be the maximum k such that
$((y_1,z_1),\ldots ,(y_s,z_s))$
to be the maximum k such that
![]() $((y_1,z_1),\ldots ,(y_s,z_s))$
is k-degenerate.
$((y_1,z_1),\ldots ,(y_s,z_s))$
is k-degenerate.
Note that
![]() $(y_1,z_1,\ldots ,y_s,z_s)$
is always
$(y_1,z_1,\ldots ,y_s,z_s)$
is always
![]() $0$
-degenerate (so the definition of degeneracy is well defined).
$0$
-degenerate (so the definition of degeneracy is well defined).
The significance of the matrix
![]() $M(y_1,z_1,\ldots ,y_s,z_s)$
is as follows. For any subset
$M(y_1,z_1,\ldots ,y_s,z_s)$
is as follows. For any subset
![]() $U\subseteq V(G)$
the entries of the product
$U\subseteq V(G)$
the entries of the product
![]() $M(y_1,z_1,\ldots ,y_s,z_s)\vec {1}_U$
(which is a vector with s entries) are precisely
$M(y_1,z_1,\ldots ,y_s,z_s)\vec {1}_U$
(which is a vector with s entries) are precisely
![]() $|N(z_i)\cap (U\setminus \{y_i\})|-|N(y_i)\cap (U\setminus \{z_i\})|$
for
$|N(z_i)\cap (U\setminus \{y_i\})|-|N(y_i)\cap (U\setminus \{z_i\})|$
for
![]() $i=1,\ldots ,s$
(these quantities occur in the definition of
$i=1,\ldots ,s$
(these quantities occur in the definition of
![]() $Y_{\ell }$
in Lemma 13.4). We can obtain a bound on the joint anticoncentration of these quantities from the following version of a theorem of Halász [Reference Halász55] (which can be viewed as a multidimensional version of the Erdős–Littlewood–Offord theorem [Reference Erdős32]). This version follows via a fairly short deduction from the standard version of Halász’ theorem [Reference Halász55, Theorem 1] (for the case
$Y_{\ell }$
in Lemma 13.4). We can obtain a bound on the joint anticoncentration of these quantities from the following version of a theorem of Halász [Reference Halász55] (which can be viewed as a multidimensional version of the Erdős–Littlewood–Offord theorem [Reference Erdős32]). This version follows via a fairly short deduction from the standard version of Halász’ theorem [Reference Halász55, Theorem 1] (for the case
![]() $r=s$
, see also [Reference Tao and Vu93, Exercise 7.2.3]), but it is slightly more convenient to instead make our deduction from a version of Halász’ theorem due to Ferber, Jain and Zhao [Reference Ferber, Jain and Zhao41].
$r=s$
, see also [Reference Tao and Vu93, Exercise 7.2.3]), but it is slightly more convenient to instead make our deduction from a version of Halász’ theorem due to Ferber, Jain and Zhao [Reference Ferber, Jain and Zhao41].
Theorem 13.8. Fix integers
![]() $s\geq r\geq 0$
and
$s\geq r\geq 0$
and
![]() $\lambda>0$
, and consider a matrix
$\lambda>0$
, and consider a matrix
![]() $M\in \mathbb {R}^{s\times n}$
. Suppose that whenever we delete at most
$M\in \mathbb {R}^{s\times n}$
. Suppose that whenever we delete at most
![]() $\lambda n$
columns of M, the resulting matrix still has rank at least r. Then for a uniformly random vector
$\lambda n$
columns of M, the resulting matrix still has rank at least r. Then for a uniformly random vector
![]() $\vec {\xi }\in \{0,1\}^{n}$
, we have
$\vec {\xi }\in \{0,1\}^{n}$
, we have
![]() $\Pr [M\vec {\xi }=\vec {\lambda }]\lesssim _{s,\lambda } n^{-r/2}$
for any vector
$\Pr [M\vec {\xi }=\vec {\lambda }]\lesssim _{s,\lambda } n^{-r/2}$
for any vector
![]() $\vec {\lambda }\in \mathbb {R}^s$
.
$\vec {\lambda }\in \mathbb {R}^s$
.
Proof. The assumption on M implies that the set of columns of M contains
![]() $\lceil \lambda n/r\rceil $
disjoint linearly independent subsets of size r (indeed, consider a maximal collection of such subsets, and note that upon deleting the corresponding columns from M the resulting matrix has rank less than r). Hence, the columns of M can be partitioned into
$\lceil \lambda n/r\rceil $
disjoint linearly independent subsets of size r (indeed, consider a maximal collection of such subsets, and note that upon deleting the corresponding columns from M the resulting matrix has rank less than r). Hence, the columns of M can be partitioned into
![]() $\lceil \lambda n/r\rceil $
subsets such that the span of each of these subsets has dimension at least r. By [Reference Ferber, Jain and Zhao41, Theorem 1.10], this implies that
$\lceil \lambda n/r\rceil $
subsets such that the span of each of these subsets has dimension at least r. By [Reference Ferber, Jain and Zhao41, Theorem 1.10], this implies that
![]() $\Pr [M\vec {\xi }=\vec {\lambda }]\lesssim _{s} (\lceil \lambda n/r\rceil )^{-r/2} \lesssim _{s,\lambda } n^{-r/2}$
.
$\Pr [M\vec {\xi }=\vec {\lambda }]\lesssim _{s} (\lceil \lambda n/r\rceil )^{-r/2} \lesssim _{s,\lambda } n^{-r/2}$
.
Applying this theorem to the matrix-vector product
![]() $M(y_1,z_1,\ldots ,y_s,z_s)\vec {1}_U$
yields bounds that get weaker as the degeneracy of
$M(y_1,z_1,\ldots ,y_s,z_s)\vec {1}_U$
yields bounds that get weaker as the degeneracy of
![]() $((y_1,z_1),\ldots ,(y_s,z_s))$
increases. We therefore need to show that there are only few s-tuples
$((y_1,z_1),\ldots ,(y_s,z_s))$
increases. We therefore need to show that there are only few s-tuples
![]() $((y_1,z_1),\ldots ,(y_s,z_s))\in T^s$
with high degeneracy (see part (b) of Lemma 13.10 below), and we will use the following technical lemma to do this.
$((y_1,z_1),\ldots ,(y_s,z_s))\in T^s$
with high degeneracy (see part (b) of Lemma 13.10 below), and we will use the following technical lemma to do this.
Lemma 13.9. For a C-Ramsey graph G on n vertices (where n is sufficiently large with respect to C), let
![]() $S\subseteq S_0\subseteq V(G)$
,
$S\subseteq S_0\subseteq V(G)$
,
![]() $T\subseteq V(G)^2$
,
$T\subseteq V(G)^2$
,
![]() $D = D(C)$
,
$D = D(C)$
,
![]() $\rho =\rho (C)>0$
and
$\rho =\rho (C)>0$
and
![]() $\delta =\delta (C)>0$
be defined as in Lemma 13.4. Let
$\delta =\delta (C)>0$
be defined as in Lemma 13.4. Let
![]() $((y_1,z_1),\ldots ,(y_s,z_s))\in T^s$
be a k-degenerate s-tuple for some
$((y_1,z_1),\ldots ,(y_s,z_s))\in T^s$
be a k-degenerate s-tuple for some
![]() $0\leq s\leq D/2$
and
$0\leq s\leq D/2$
and
![]() $k\in \{0,\ldots ,s\}$
. Then there exist indices
$k\in \{0,\ldots ,s\}$
. Then there exist indices
![]() $1\leq i_1<\cdots <i_{s-k}\leq s$
such that the following holds. For every vector
$1\leq i_1<\cdots <i_{s-k}\leq s$
such that the following holds. For every vector
![]() $\vec {t}\in \{-1,0,1\}^{s-k}$
, let
$\vec {t}\in \{-1,0,1\}^{s-k}$
, let
![]() $W_{\vec {t}}\subseteq V(G)$
be the set of vertices such that the corresponding column of the
$W_{\vec {t}}\subseteq V(G)$
be the set of vertices such that the corresponding column of the
![]() $(s-k)\times n$
matrix
$(s-k)\times n$
matrix
![]() $M(y_{i_1},z_{i_1},\ldots ,y_{i_{s-k}},z_{i_{s-k}})$
(as in Definition 13.7) equals
$M(y_{i_1},z_{i_1},\ldots ,y_{i_{s-k}},z_{i_{s-k}})$
(as in Definition 13.7) equals
![]() $\vec {t}$
. Then for each
$\vec {t}$
. Then for each
![]() $j\in [s]\setminus \{i_1,\ldots ,i_{s-k}\}$
one can find a vector
$j\in [s]\setminus \{i_1,\ldots ,i_{s-k}\}$
one can find a vector
![]() $\vec {t}\in \{-1,0,1\}^{s-k}$
such that the set
$\vec {t}\in \{-1,0,1\}^{s-k}$
such that the set
![]() $W_{\vec {t}}$
fulfills the following three conditions:
$W_{\vec {t}}$
fulfills the following three conditions:
-
(i)
 $|W_{\vec {t}}\cap S_0|\geq \delta \cdot |S_0|$
.
$|W_{\vec {t}}\cap S_0|\geq \delta \cdot |S_0|$
. -
(ii)
 $|N(y_j)\cap W_{\vec {t}}\cap S_0|\leq \rho \cdot |W_{\vec {t}}\cap S_0|$
.
$|N(y_j)\cap W_{\vec {t}}\cap S_0|\leq \rho \cdot |W_{\vec {t}}\cap S_0|$
. -
(iii)
 $|N(z_j)\cap W_{\vec {t}}\cap S_0|\geq (1-\rho )\cdot |W_{\vec {t}}\cap S_0|$
.
$|N(z_j)\cap W_{\vec {t}}\cap S_0|\geq (1-\rho )\cdot |W_{\vec {t}}\cap S_0|$
.
Proof. Since
![]() $((y_1,z_1),\ldots ,(y_s,z_s))\in T^s$
is k-degenerate, there is a way to delete at most
$((y_1,z_1),\ldots ,(y_s,z_s))\in T^s$
is k-degenerate, there is a way to delete at most
![]() $\delta ^{3/\rho }\cdot n$
columns from the
$\delta ^{3/\rho }\cdot n$
columns from the
![]() $s\times n$
matrix
$s\times n$
matrix
![]() $M(y_1,z_1,\ldots ,y_s,z_s)$
and obtain a matrix
$M(y_1,z_1,\ldots ,y_s,z_s)$
and obtain a matrix
![]() $M'$
of rank at most
$M'$
of rank at most
![]() $s-k$
. Let
$s-k$
. Let
![]() $Q\subseteq V(G)$
be the set of vertices corresponding to the deleted columns. We have the bound
$Q\subseteq V(G)$
be the set of vertices corresponding to the deleted columns. We have the bound
![]() $|Q|+2\leq \delta ^{3/\rho }\cdot n+2\leq \delta ^{2/\rho }\cdot |S_0|+2\leq \delta \cdot |S_0|\leq (\rho ^2/2)\cdot |S_0|$
(recall from Lemma 13.1 that
$|Q|+2\leq \delta ^{3/\rho }\cdot n+2\leq \delta ^{2/\rho }\cdot |S_0|+2\leq \delta \cdot |S_0|\leq (\rho ^2/2)\cdot |S_0|$
(recall from Lemma 13.1 that
![]() $|S_0|\ge \delta ^{1/\rho }\cdot n$
and
$|S_0|\ge \delta ^{1/\rho }\cdot n$
and
![]() $\delta <\rho ^3/3^{D+1}$
).
$\delta <\rho ^3/3^{D+1}$
).
Since
![]() $M'$
has rank at most
$M'$
has rank at most
![]() $s-k$
, we can choose indices
$s-k$
, we can choose indices
![]() $1\leq i_1<\cdots <i_{s-k}\leq s$
such that every row of
$1\leq i_1<\cdots <i_{s-k}\leq s$
such that every row of
![]() $M'$
can be written as a linear combination of the rows with indices
$M'$
can be written as a linear combination of the rows with indices
![]() $i_1,\ldots ,i_{s-k}$
. We will show that this choice of indices satisfies the desired statement.
$i_1,\ldots ,i_{s-k}$
. We will show that this choice of indices satisfies the desired statement.
The rows of
![]() $M'$
with indices
$M'$
with indices
![]() $i_1,\ldots ,i_{s-k}$
form precisely the matrix
$i_1,\ldots ,i_{s-k}$
form precisely the matrix
![]() $M(y_{i_1},z_{i_1},\ldots ,y_{i_{s-k}},z_{i_{s-k}})$
with the columns corresponding to vertices in Q deleted. Note that for each vector
$M(y_{i_1},z_{i_1},\ldots ,y_{i_{s-k}},z_{i_{s-k}})$
with the columns corresponding to vertices in Q deleted. Note that for each vector
![]() $\vec {t}\in \{-1,0,1\}^{s-k}$
and each
$\vec {t}\in \{-1,0,1\}^{s-k}$
and each
![]() $h=1,\ldots ,s-k$
, the entries in the
$h=1,\ldots ,s-k$
, the entries in the
![]() $i_h$
-th row of
$i_h$
-th row of
![]() $M'$
in the columns with indices in
$M'$
in the columns with indices in
![]() $W_{\vec {t}}\setminus Q$
all have the same value, namely
$W_{\vec {t}}\setminus Q$
all have the same value, namely
![]() $t_h$
. In other words, writing
$t_h$
. In other words, writing
for the j-th row of
![]() $M'$
for
$M'$
for
![]() $j=1,\ldots ,s$
, each of the row vectors
$j=1,\ldots ,s$
, each of the row vectors
![]() $\vec M^{\prime }_{i_1},\ldots ,\vec M^{\prime }_{i_{s-k}}$
are constant on each of the column sets
$\vec M^{\prime }_{i_1},\ldots ,\vec M^{\prime }_{i_{s-k}}$
are constant on each of the column sets
![]() $W_{\vec {t}}\setminus Q$
, for
$W_{\vec {t}}\setminus Q$
, for
![]() $\vec {t}\in \{-1,0,1\}^{s-k}$
. Since every row
$\vec {t}\in \{-1,0,1\}^{s-k}$
. Since every row
![]() $\vec M^{\prime }_j$
is a linear combination of these vectors, it follows that in fact each row
$\vec M^{\prime }_j$
is a linear combination of these vectors, it follows that in fact each row
![]() $\vec M^{\prime }_j$
is constant on each of the column sets
$\vec M^{\prime }_j$
is constant on each of the column sets
![]() $W_{\vec {t}}\setminus Q$
.
$W_{\vec {t}}\setminus Q$
.
Now, let us fix some
![]() $j\in [s]\setminus \{i_1,\ldots ,i_{s-k}\}$
. We need to show that we can find some
$j\in [s]\setminus \{i_1,\ldots ,i_{s-k}\}$
. We need to show that we can find some
![]() $\vec {t}\in \{-1,0,1\}^{s-k}$
satisfying conditions (i)–(iii) in the lemma. Since
$\vec {t}\in \{-1,0,1\}^{s-k}$
satisfying conditions (i)–(iii) in the lemma. Since
![]() $(y_j,z_j)\in T$
, the definition of T (see the statement of Lemma 13.4) implies
$(y_j,z_j)\in T$
, the definition of T (see the statement of Lemma 13.4) implies
![]() $|(N(z_j)\setminus N(y_j))\cap S_0|\geq \rho ^2 \cdot |S_0|$
, and so
$|(N(z_j)\setminus N(y_j))\cap S_0|\geq \rho ^2 \cdot |S_0|$
, and so
![]() $|(N(z_j)\setminus N(y_j))\cap (S_0\setminus (Q\cup \{y_j,z_j\}))|\geq \rho ^2 \cdot |S_0|-|Q|-2\geq (\rho ^2/2)\cdot |S_0|$
. This means that
$|(N(z_j)\setminus N(y_j))\cap (S_0\setminus (Q\cup \{y_j,z_j\}))|\geq \rho ^2 \cdot |S_0|-|Q|-2\geq (\rho ^2/2)\cdot |S_0|$
. This means that
![]() $\vec M^{\prime }_j$
has at least
$\vec M^{\prime }_j$
has at least
![]() $(\rho ^2/2)|S_0|$
entries corresponding to vertices in
$(\rho ^2/2)|S_0|$
entries corresponding to vertices in
![]() $S_0\setminus (Q\cup \{y_j,z_j\})$
with value
$S_0\setminus (Q\cup \{y_j,z_j\})$
with value
![]() $1-0=1$
. Hence, by the pigeonhole principle there must be some
$1-0=1$
. Hence, by the pigeonhole principle there must be some
![]() $\vec {t}\in \{-1,0,1\}^{s-k}$
for which there are at least
$\vec {t}\in \{-1,0,1\}^{s-k}$
for which there are at least
![]() $\rho ^2\cdot |S_0|/(2\cdot 3^{s-k})\geq (\rho ^2/3^{D+1})\cdot |S_0|$
vertices in
$\rho ^2\cdot |S_0|/(2\cdot 3^{s-k})\geq (\rho ^2/3^{D+1})\cdot |S_0|$
vertices in
![]() $(W_{\vec {t}}\cap S_0)\setminus (Q\cup \{y_j,z_j\})$
such that the corresponding entry in
$(W_{\vec {t}}\cap S_0)\setminus (Q\cup \{y_j,z_j\})$
such that the corresponding entry in
![]() $\vec M^{\prime }_j$
is 1.
$\vec M^{\prime }_j$
is 1.
For this
![]() $\vec t$
, we have
$\vec t$
, we have
![]() $|W_{\vec {t}}\cap S_0|\geq (\rho ^2/3^{D+1})\cdot |S_0|\geq (\delta /\rho )\cdot |S_0|$
, so
$|W_{\vec {t}}\cap S_0|\geq (\rho ^2/3^{D+1})\cdot |S_0|\geq (\delta /\rho )\cdot |S_0|$
, so
![]() $\vec {t}$
satisfies (i) (recall from Lemma 13.1 that
$\vec {t}$
satisfies (i) (recall from Lemma 13.1 that
![]() $0<\rho <1$
). Furthermore, recall that
$0<\rho <1$
). Furthermore, recall that
![]() $\vec M^{\prime }_j$
is constant on the index set
$\vec M^{\prime }_j$
is constant on the index set
![]() $W_{\vec {t}}\setminus Q$
, so this constant value must be 1. This means that for all vertices
$W_{\vec {t}}\setminus Q$
, so this constant value must be 1. This means that for all vertices
![]() $v\in W_{\vec {t}}\setminus (Q\cup \{y_j,z_j\})$
we must have
$v\in W_{\vec {t}}\setminus (Q\cup \{y_j,z_j\})$
we must have
![]() $v\in N(z_i)$
and
$v\in N(z_i)$
and
![]() $v\not \in N(y_i)$
. Hence,
$v\not \in N(y_i)$
. Hence,
![]() $|N(y_j)\cap W_{\vec {t}}\cap S_0|\leq |Q\cup \{y_j,z_j\}|\leq |Q|+2\leq \delta \cdot |S_0|\le \rho \cdot |W_{\vec {t}}\cap S_0|$
, establishing (ii). Furthermore, we similarly have
$|N(y_j)\cap W_{\vec {t}}\cap S_0|\leq |Q\cup \{y_j,z_j\}|\leq |Q|+2\leq \delta \cdot |S_0|\le \rho \cdot |W_{\vec {t}}\cap S_0|$
, establishing (ii). Furthermore, we similarly have
![]() $|N(z_j)\cap W_{\vec {t}}\cap S_0|\geq |W_{\vec {t}}\cap S_0|-|Q\cup \{y_j,z_j\}|\geq (1-\rho )\cdot |W_{\vec {t}}\cap S_0|$
as required in (iii).
$|N(z_j)\cap W_{\vec {t}}\cap S_0|\geq |W_{\vec {t}}\cap S_0|-|Q\cup \{y_j,z_j\}|\geq (1-\rho )\cdot |W_{\vec {t}}\cap S_0|$
as required in (iii).
Given a graph G and vertex pairs
![]() $(y_1,z_1),\ldots ,(y_s,z_s)\in V(G)^2$
, for each
$(y_1,z_1),\ldots ,(y_s,z_s)\in V(G)^2$
, for each
![]() $i=1,\ldots ,s$
, define
$i=1,\ldots ,s$
, define
to be the set of vertices in
![]() $V(G)\setminus \{y_1,z_1,\ldots ,y_s,z_s\}$
that are adjacent to
$V(G)\setminus \{y_1,z_1,\ldots ,y_s,z_s\}$
that are adjacent to
![]() $z_i$
but not to any of the other vertices among
$z_i$
but not to any of the other vertices among
![]() $y_1,z_1,\ldots ,y_s,z_s$
. For the lower bound in Lemma 13.4, we will consider tuples
$y_1,z_1,\ldots ,y_s,z_s$
. For the lower bound in Lemma 13.4, we will consider tuples
![]() $((y_1,z_1),\ldots ,(y_s,z_s))\in T^s$
such that
$((y_1,z_1),\ldots ,(y_s,z_s))\in T^s$
such that
![]() $|N_i(y_1,z_1,\ldots ,y_s,z_s)\cap S_0|\geq \rho \delta \cdot |S_0|$
for all
$|N_i(y_1,z_1,\ldots ,y_s,z_s)\cap S_0|\geq \rho \delta \cdot |S_0|$
for all
![]() $i=1,\ldots ,s$
.
$i=1,\ldots ,s$
.
Lemma 13.10. For a C-Ramsey graph G on n vertices (where n is sufficiently large with respect to C), let
![]() $S\subseteq S_0\subseteq V(G)$
,
$S\subseteq S_0\subseteq V(G)$
,
![]() $T\subseteq V(G)^2$
,
$T\subseteq V(G)^2$
,
![]() $D = D(C)$
,
$D = D(C)$
,
![]() $\rho =\rho (C)>0$
and
$\rho =\rho (C)>0$
and
![]() $\delta =\delta (C)>0$
be defined as in Lemma 13.4. Then for each
$\delta =\delta (C)>0$
be defined as in Lemma 13.4. Then for each
![]() $s=0,1,\ldots ,D/2$
the following statements hold.
$s=0,1,\ldots ,D/2$
the following statements hold.
-
(a) At least
 $|T|^s/2$
different s-tuples
$|T|^s/2$
different s-tuples
 $((y_1,z_1),\ldots ,(y_s,z_s))\in T^s$
with distinct
$((y_1,z_1),\ldots ,(y_s,z_s))\in T^s$
with distinct
 $y_1,z_1,\ldots ,y_s,z_s$
satisfy
$y_1,z_1,\ldots ,y_s,z_s$
satisfy
 $|N_i(y_1,z_1,\ldots ,y_s,z_s)\cap S_0|\geq \rho \delta \cdot |S_0|$
for all
$|N_i(y_1,z_1,\ldots ,y_s,z_s)\cap S_0|\geq \rho \delta \cdot |S_0|$
for all
 $i=1,\ldots ,s$
.
$i=1,\ldots ,s$
. -
(b) For each
 $k=0,\ldots ,s$
, the number of k-degenerate s-tuples
$k=0,\ldots ,s$
, the number of k-degenerate s-tuples
 $((y_1,z_1),\ldots ,(y_s,z_s))\in T^s$
is at most
$((y_1,z_1),\ldots ,(y_s,z_s))\in T^s$
is at most
 $|T|^s/\sqrt {n}^k$
.
$|T|^s/\sqrt {n}^k$
.
Proof. For (a), we first claim that for each fixed
![]() $i=1,\ldots ,s$
there are at most
$i=1,\ldots ,s$
there are at most
![]() $|T|^s/(4D)$
different s-tuples
$|T|^s/(4D)$
different s-tuples
![]() $((y_1,z_1),\ldots ,(y_s,z_s))\in T^s$
with
$((y_1,z_1),\ldots ,(y_s,z_s))\in T^s$
with
![]() $|N_i(y_1,z_1,\ldots ,y_s,z_s)\cap S_0|< \rho \delta \cdot |S_0|$
. Indeed, without loss of generality assume
$|N_i(y_1,z_1,\ldots ,y_s,z_s)\cap S_0|< \rho \delta \cdot |S_0|$
. Indeed, without loss of generality assume
![]() $i=s$
and note that there are
$i=s$
and note that there are
![]() $|T|^{s-1}$
choices for the pairs
$|T|^{s-1}$
choices for the pairs
![]() $(y_1,z_1),\ldots ,(y_{s-1},z_{s-1})$
and
$(y_1,z_1),\ldots ,(y_{s-1},z_{s-1})$
and
![]() $|S|$
choices for
$|S|$
choices for
![]() $y_s$
. Fixing these choices determines the set
$y_s$
. Fixing these choices determines the set
![]() $\overline {N}(y_1,z_1,\ldots ,y_{s-1},z_{s-1},y_s)$
and by property (2) of Lemma 13.1 this set satisfies
$\overline {N}(y_1,z_1,\ldots ,y_{s-1},z_{s-1},y_s)$
and by property (2) of Lemma 13.1 this set satisfies
Hence, since the graph
![]() $G[S_0]$
is
$G[S_0]$
is
![]() $(\delta ,\rho )$
-rich (by property (1) of Lemma 13.1), there are at most
$(\delta ,\rho )$
-rich (by property (1) of Lemma 13.1), there are at most
![]() $n^{1/5}$
choices for the remaining vertex
$n^{1/5}$
choices for the remaining vertex
![]() $z_s$
such that the set
$z_s$
such that the set
has size at most
![]() $\rho \cdot |\overline {N}(y_1,z_1,\ldots ,y_{s-1},z_{-1},y_s)\cap S_0|$
. In particular, there are at most
$\rho \cdot |\overline {N}(y_1,z_1,\ldots ,y_{s-1},z_{-1},y_s)\cap S_0|$
. In particular, there are at most
![]() $n^{1/5}$
choices for
$n^{1/5}$
choices for
![]() $z_s$
with
$z_s$
with
![]() $|N_s(y_1,z_1,\ldots ,y_s,z_s)\cap S_0|< \rho \delta \cdot |S_0|$
.
$|N_s(y_1,z_1,\ldots ,y_s,z_s)\cap S_0|< \rho \delta \cdot |S_0|$
.
This indeed shows that for each
![]() $i=1,\ldots ,s$
there are at most
$i=1,\ldots ,s$
there are at most
![]() $|T|^{s-1}\cdot |S|\cdot n^{1/5}\leq |T|^{s}/(4D)$
different s-tuples
$|T|^{s-1}\cdot |S|\cdot n^{1/5}\leq |T|^{s}/(4D)$
different s-tuples
![]() $((y_1,z_1),\ldots ,(y_s,z_s))\in T^s$
with
$((y_1,z_1),\ldots ,(y_s,z_s))\in T^s$
with
![]() $|N_i(y_1,z_1,\ldots ,y_s,z_s)\cap S_0|< \rho \delta \cdot |S_0|$
(recall from Lemma 13.5 that
$|N_i(y_1,z_1,\ldots ,y_s,z_s)\cap S_0|< \rho \delta \cdot |S_0|$
(recall from Lemma 13.5 that
![]() $|T|\geq |S|^2/2\geq |S|\cdot n^{0.48}/2$
). Hence, there are at least
$|T|\geq |S|^2/2\geq |S|\cdot n^{0.48}/2$
). Hence, there are at least
![]() $(3/4)\cdot |T|^s$
different s-tuples
$(3/4)\cdot |T|^s$
different s-tuples
![]() $((y_1,z_1),\ldots ,(y_s,z_s))\in T^s$
with
$((y_1,z_1),\ldots ,(y_s,z_s))\in T^s$
with
![]() $|N_i(y_1,z_1,\ldots ,y_s,z_s)\cap S_0|\geq \rho \delta \cdot |S_0|$
for all
$|N_i(y_1,z_1,\ldots ,y_s,z_s)\cap S_0|\geq \rho \delta \cdot |S_0|$
for all
![]() $i=1,\ldots ,s$
. Now, at most
$i=1,\ldots ,s$
. Now, at most
![]() $O_s(|T|^{s-1}\cdot |S|)\leq |T|^s/4$
of these s-tuples can have a repetition among the vertices
$O_s(|T|^{s-1}\cdot |S|)\leq |T|^s/4$
of these s-tuples can have a repetition among the vertices
![]() $y_1,z_1,\ldots ,y_s,z_s$
. This proves (a).
$y_1,z_1,\ldots ,y_s,z_s$
. This proves (a).
For (b), fix some
![]() $k\in \{0,\ldots ,s\}$
. For each k-degenerate s-tuple
$k\in \{0,\ldots ,s\}$
. For each k-degenerate s-tuple
![]() $((y_1,z_1),\ldots ,(y_s,z_s))\in T^s$
we can find indices
$((y_1,z_1),\ldots ,(y_s,z_s))\in T^s$
we can find indices
![]() $1\leq i_1<\cdots <i_{s-k}\leq s$
with the property in Lemma 13.9. It suffices to show that for any fixed
$1\leq i_1<\cdots <i_{s-k}\leq s$
with the property in Lemma 13.9. It suffices to show that for any fixed
![]() $1\leq i_1<\cdots <i_{s-k}\leq s$
, there are at most
$1\leq i_1<\cdots <i_{s-k}\leq s$
, there are at most
![]() $|T|^s/(\sqrt {n}^k\cdot \binom {s}{k})$
different s-tuples
$|T|^s/(\sqrt {n}^k\cdot \binom {s}{k})$
different s-tuples
![]() $((y_1,z_1),\ldots ,(y_s,z_s))\in T^s$
with the property in Lemma 13.9. To show this, first note that there are
$((y_1,z_1),\ldots ,(y_s,z_s))\in T^s$
with the property in Lemma 13.9. To show this, first note that there are
![]() $|T|^{s-k}$
choices for
$|T|^{s-k}$
choices for
![]() $(y_{i_1},z_{i_1}),\ldots ,(y_{i_{s-k}},z_{i_{s-k}})\in T$
. After fixing these choices, we claim that for each
$(y_{i_1},z_{i_1}),\ldots ,(y_{i_{s-k}},z_{i_{s-k}})\in T$
. After fixing these choices, we claim that for each
![]() $j\in [s]\setminus \{i_1,\ldots ,i_{s-k}\}$
there are at most
$j\in [s]\setminus \{i_1,\ldots ,i_{s-k}\}$
there are at most
![]() $3^{s-k}\cdot n^{2/5}$
possibilities for the vertices
$3^{s-k}\cdot n^{2/5}$
possibilities for the vertices
![]() $y_j$
and
$y_j$
and
![]() $z_j$
. Indeed, for every such j there must be a vector
$z_j$
. Indeed, for every such j there must be a vector
![]() $\vec {t}\in \{-1,0,1\}^{s-k}$
such that conditions (i) to (iii) in Lemma 13.9 hold. There are at most
$\vec {t}\in \{-1,0,1\}^{s-k}$
such that conditions (i) to (iii) in Lemma 13.9 hold. There are at most
![]() $3^{s-k}$
possibilities for
$3^{s-k}$
possibilities for
![]() $\vec {t}$
satisfying (i), and whenever (i) holds there are at most
$\vec {t}$
satisfying (i), and whenever (i) holds there are at most
![]() $n^{1/5}$
choices for
$n^{1/5}$
choices for
![]() $y_j$
satisfying (ii) and at most
$y_j$
satisfying (ii) and at most
![]() $n^{1/5}$
choices for
$n^{1/5}$
choices for
![]() $z_j$
satisfying (iii), since the graph
$z_j$
satisfying (iii), since the graph
![]() $G[S_0]$
is
$G[S_0]$
is
![]() $(\delta ,\rho )$
-rich. So overall, for fixed indices
$(\delta ,\rho )$
-rich. So overall, for fixed indices
![]() $1\leq i_1<\cdots <i_{s-k}\leq s$
, there are indeed at most
$1\leq i_1<\cdots <i_{s-k}\leq s$
, there are indeed at most
![]() $|T|^{s-k}\cdot (3^{s-k}n^{2/5})^{k}\leq 3^{Dk}\cdot |T|^{s-k} \cdot (n^{0.4})^k\leq |T|^s/(\sqrt {n}^k\cdot \binom {s}{k})$
different s-tuples
$|T|^{s-k}\cdot (3^{s-k}n^{2/5})^{k}\leq 3^{Dk}\cdot |T|^{s-k} \cdot (n^{0.4})^k\leq |T|^s/(\sqrt {n}^k\cdot \binom {s}{k})$
different s-tuples
![]() $((y_1,z_1),\ldots ,(y_s,z_s))\in T^s$
satisfying the property in Lemma 13.9 for n sufficiently large (recalling that
$((y_1,z_1),\ldots ,(y_s,z_s))\in T^s$
satisfying the property in Lemma 13.9 for n sufficiently large (recalling that
![]() $|T|\geq n^{0.96}/2$
by Lemma 13.5).
$|T|\geq n^{0.96}/2$
by Lemma 13.5).
Now, we prove Lemma 13.4.
Proof of Lemma 13.4
We may assume that n is sufficiently large with respect to C and A. Let
![]() $X=e(G[U])+\sum _{u\in U}e_u$
, and let us define
$X=e(G[U])+\sum _{u\in U}e_u$
, and let us define
![]() $E=\mathbb {E}X$
. Consider
$E=\mathbb {E}X$
. Consider
![]() $x\in \mathbb Z$
such that
$x\in \mathbb Z$
such that
![]() $|x-E|\leq An^{3/2}$
, and fix
$|x-E|\leq An^{3/2}$
, and fix
![]() $a_{-B},\ldots ,a_B\in \{0,1,2\}$
. Let
$a_{-B},\ldots ,a_B\in \{0,1,2\}$
. Let
![]() $s=a_{-B}+\cdots +a_B\leq 4B+2$
, and fix a list
$s=a_{-B}+\cdots +a_B\leq 4B+2$
, and fix a list
![]() $(\ell _{1},\ldots ,\ell _{s})$
containing
$(\ell _{1},\ldots ,\ell _{s})$
containing
![]() $a_{\ell }$
copies of each
$a_{\ell }$
copies of each
![]() $\ell =-B,\ldots ,B$
. For
$\ell =-B,\ldots ,B$
. For
![]() $(y,z)\in T$
, let
$(y,z)\in T$
, let
![]() $\mathcal {E}_i(y,z)$
be the event that
$\mathcal {E}_i(y,z)$
be the event that
![]() $(y,z)$
contributes to
$(y,z)$
contributes to
![]() $Y_{\ell _i}$
; that is, the event that we have
$Y_{\ell _i}$
; that is, the event that we have
![]() $y\in U$
and
$y\in U$
and
![]() $z\notin U$
and
$z\notin U$
and
![]() $(|N(z)\cap (U\setminus \{y\})|+e_z)-(|N(y)\cap (U\setminus \{x\})|+e_y)=\ell _i$
. Now,
$(|N(z)\cap (U\setminus \{y\})|+e_z)-(|N(y)\cap (U\setminus \{x\})|+e_y)=\ell _i$
. Now,
where the sum is over all s-tuples
![]() $((y_1,z_1),\ldots ,(y_s,z_s))\in T^s$
. To prove the lemma, we separately establish lower and upper bounds on this quantity. Note that for
$((y_1,z_1),\ldots ,(y_s,z_s))\in T^s$
. To prove the lemma, we separately establish lower and upper bounds on this quantity. Note that for
![]() $s=0$
, we already know that
$s=0$
, we already know that
![]() $\Pr [|X-x|\leq B] \asymp _{C,H,A} n^{-3/2}$
by Theorem 3.1, so we may assume that
$\Pr [|X-x|\leq B] \asymp _{C,H,A} n^{-3/2}$
by Theorem 3.1, so we may assume that
![]() $s\geq 1$
.
$s\geq 1$
.
Step 1: the lower bound. For the lower bound, we will only consider the contribution to (13.1) from s-tuples in
![]() $T^s$
satisfying Lemma 13.10(a). There are at least
$T^s$
satisfying Lemma 13.10(a). There are at least
![]() $|T|^s/2$
such s-tuples. So in order to establish the desired lower bound
$|T|^s/2$
such s-tuples. So in order to establish the desired lower bound
![]() $\Omega _{C,H,A}((|T|/\sqrt {n})^s\cdot n^{-3/2})$
for the sum in (13.1), it suffices to prove that each such s-tuple contributes at least
$\Omega _{C,H,A}((|T|/\sqrt {n})^s\cdot n^{-3/2})$
for the sum in (13.1), it suffices to prove that each such s-tuple contributes at least
![]() $\Omega _{C,H,A}(n^{-(s+3)/2})$
to the sum. In other words, it suffices to show that
$\Omega _{C,H,A}(n^{-(s+3)/2})$
to the sum. In other words, it suffices to show that
for any s-tuple
![]() $((y_1,z_1),\ldots ,(y_s,z_s))\in T^s$
with
$((y_1,z_1),\ldots ,(y_s,z_s))\in T^s$
with
![]() $|N_i(y_1,z_1,\ldots ,y_s,z_s)\cap S_0|\geq \rho \delta |S_0|$
for all
$|N_i(y_1,z_1,\ldots ,y_s,z_s)\cap S_0|\geq \rho \delta |S_0|$
for all
![]() $i=1,\ldots ,s$
and such that the vertices
$i=1,\ldots ,s$
and such that the vertices
![]() $y_1,z_1,\ldots ,y_s,z_s$
are distinct. So let
$y_1,z_1,\ldots ,y_s,z_s$
are distinct. So let
![]() $((y_1,z_1),\ldots ,(y_s,z_s))\in T^s$
be such an s-tuple. For simplicity of notation, we write
$((y_1,z_1),\ldots ,(y_s,z_s))\in T^s$
be such an s-tuple. For simplicity of notation, we write
![]() $\overline {N}=\overline {N}(y_1,z_1,\ldots ,y_s,z_s)\cap S_0$
and
$\overline {N}=\overline {N}(y_1,z_1,\ldots ,y_s,z_s)\cap S_0$
and
![]() $N_i=N_i(y_1,z_1,\ldots ,y_s,z_s)\cap S_0$
for
$N_i=N_i(y_1,z_1,\ldots ,y_s,z_s)\cap S_0$
for
![]() $i=1,\ldots ,s$
. Then
$i=1,\ldots ,s$
. Then
![]() $|N_i|\geq \rho \delta |S_0|\ge \rho \delta ^{1+1/\rho }\cdot n$
for
$|N_i|\geq \rho \delta |S_0|\ge \rho \delta ^{1+1/\rho }\cdot n$
for
![]() $i=1,\ldots ,s$
, and also
$i=1,\ldots ,s$
, and also
![]() $|\overline {N}|\geq \delta |S_0|\geq \delta ^{1+1/\rho }\cdot n$
by property (2) of Lemma 13.1 (as
$|\overline {N}|\geq \delta |S_0|\geq \delta ^{1+1/\rho }\cdot n$
by property (2) of Lemma 13.1 (as
![]() $2s\leq 8B+4\leq D$
). Note that
$2s\leq 8B+4\leq D$
). Note that
![]() $N_1,\ldots ,N_s$
and
$N_1,\ldots ,N_s$
and
![]() $\overline {N}$
are disjoint subsets of
$\overline {N}$
are disjoint subsets of
![]() $S_0\setminus \{y_1,z_1,\ldots ,y_s,z_s\}$
. Let us write
$S_0\setminus \{y_1,z_1,\ldots ,y_s,z_s\}$
. Let us write
![]() $W=V(G)\setminus (N_1\cup \cdots \cup N_s\cup \overline {N})$
, and note that
$W=V(G)\setminus (N_1\cup \cdots \cup N_s\cup \overline {N})$
, and note that
![]() $N(y_i)\subseteq W$
and
$N(y_i)\subseteq W$
and
![]() $N(z_i)\subseteq W\cup N_i$
for
$N(z_i)\subseteq W\cup N_i$
for
![]() $i=1,\ldots ,s$
.
$i=1,\ldots ,s$
.
We will now expose the random subset
![]() $U\subseteq V(G)$
in several steps. First, we expose
$U\subseteq V(G)$
in several steps. First, we expose
![]() $U\cap W$
and consider the conditional expectation
$U\cap W$
and consider the conditional expectation
![]() $\mathbb E[X\,|\, U\cap W]$
(which is a function of the random outcome of
$\mathbb E[X\,|\, U\cap W]$
(which is a function of the random outcome of
![]() $U\cap W$
). Note that this random variable is of the form in Lemma 13.6 applied to the graph
$U\cap W$
). Note that this random variable is of the form in Lemma 13.6 applied to the graph
![]() $G[W]$
with the random set
$G[W]$
with the random set
![]() $U\cap W\subseteq W$
, with
$U\cap W\subseteq W$
, with
![]() $f_w=e_w+\deg _{V(G)\setminus W}(w)$
for all
$f_w=e_w+\deg _{V(G)\setminus W}(w)$
for all
![]() $w\in W$
, with
$w\in W$
, with
![]() $f_0 = e(V(G)\setminus W)+\sum _{v\in V(G)\setminus W}e_v$
, and with
$f_0 = e(V(G)\setminus W)+\sum _{v\in V(G)\setminus W}e_v$
, and with
![]() $R=(H+1)n/|W|$
. By Lemma 13.6(1), its variance is at most
$R=(H+1)n/|W|$
. By Lemma 13.6(1), its variance is at most
![]() $((H+1)n/|W|)^2\cdot |W|^3\le (H+1)^2n^3$
, and trivially its expectation is exactly
$((H+1)n/|W|)^2\cdot |W|^3\le (H+1)^2n^3$
, and trivially its expectation is exactly
![]() $E=\mathbb E[X]$
. Now, we claim that with probability at least
$E=\mathbb E[X]$
. Now, we claim that with probability at least
![]() $2^{-2s-2}=\Omega _C(1)$
the random outcome of
$2^{-2s-2}=\Omega _C(1)$
the random outcome of
![]() $U\cap W$
satisfies the following three properties:
$U\cap W$
satisfies the following three properties:
-
(A)
 $y_1,\ldots ,y_s\in U$
and
$y_1,\ldots ,y_s\in U$
and
 $z_1,\ldots ,z_s\notin U$
, and
$z_1,\ldots ,z_s\notin U$
, and -
(B)
 $|\mathbb E[X\,|\, U\cap W]-E|\leq 2^{s+1}(H+1)n^{3/2}$
, and
$|\mathbb E[X\,|\, U\cap W]-E|\leq 2^{s+1}(H+1)n^{3/2}$
, and -
(C) for all
 $i=1,\ldots ,s$
, the quantity
$i=1,\ldots ,s$
, the quantity
 $|U\cap W\cap (N(z_i)\setminus \{y_i\})|=|U\cap (N(z_i)\setminus (\{y_i\}\cup N_i))|$
differs from
$|U\cap W\cap (N(z_i)\setminus \{y_i\})|=|U\cap (N(z_i)\setminus (\{y_i\}\cup N_i))|$
differs from
 $|N(z_i)\setminus (\{y_i\}\cup N_i)|/2$
by at most
$|N(z_i)\setminus (\{y_i\}\cup N_i)|/2$
by at most
 $2^{s+1}s\sqrt {n}$
and similarly
$2^{s+1}s\sqrt {n}$
and similarly
 $|U\cap W\cap (N(y_i)\setminus \{z_i\})|=|U\cap (N(y_i)\setminus \{z_i\})|$
differs from
$|U\cap W\cap (N(y_i)\setminus \{z_i\})|=|U\cap (N(y_i)\setminus \{z_i\})|$
differs from
 $|N(y_i)\setminus \{z_i\}|/2$
by at most
$|N(y_i)\setminus \{z_i\}|/2$
by at most
 $2^{s+1}s\sqrt {n}$
.
$2^{s+1}s\sqrt {n}$
.
Indeed, (A) holds with probability exactly
![]() $2^{-2s}$
, and by Chebyshev’s inequality, (B) and (C) fail with probability at most
$2^{-2s}$
, and by Chebyshev’s inequality, (B) and (C) fail with probability at most
![]() $2^{-2s-2}$
and
$2^{-2s-2}$
and
![]() $2s\cdot 2^{-2s-2}/s^2$
, respectively.
$2s\cdot 2^{-2s-2}/s^2$
, respectively.
From now on, we condition on an outcome of
![]() $U\cap W$
satisfying (A–C). Next, we expose
$U\cap W$
satisfying (A–C). Next, we expose
![]() $U\cap (N_1\cup \cdots \cup N_s)$
, which then determines all of
$U\cap (N_1\cup \cdots \cup N_s)$
, which then determines all of
![]() $U\setminus \overline {N}$
and in particular determines whether the events
$U\setminus \overline {N}$
and in particular determines whether the events
![]() $\mathcal {E}_i(y_{i},z_{i})$
for
$\mathcal {E}_i(y_{i},z_{i})$
for
![]() $i=1,\ldots ,s$
hold. More precisely, after fixing the outcome of
$i=1,\ldots ,s$
hold. More precisely, after fixing the outcome of
![]() $U\cap W$
, for each
$U\cap W$
, for each
![]() $i=1,\ldots ,s$
the event
$i=1,\ldots ,s$
the event
![]() $\mathcal {E}_i(y_{i},z_{i})$
is now determined by
$\mathcal {E}_i(y_{i},z_{i})$
is now determined by
![]() $U\cap N_i$
and holds if and only if
$U\cap N_i$
and holds if and only if
In particular, the quantity on the right-hand side is determined given the information
![]() $U\cap W$
. By (C), this quantity differs by at most
$U\cap W$
. By (C), this quantity differs by at most
![]() $2^{s+2}s\sqrt {n}\leq 2^{D+2}D\sqrt {n}$
from
$2^{s+2}s\sqrt {n}\leq 2^{D+2}D\sqrt {n}$
from
 $$ \begin{align*} &-|N(z_i)\setminus (\{y_i\}\cup N_i)|/2-e_{z_i}+|N(y_i)\setminus \{z_i\}|/2+e_{y_i}+\ell_i\\ &\qquad \qquad =|N_i|/2-|N(z_i)\setminus \{y_i\}|/2-e_{z_i}+|N(y_i)\setminus \{z_i\}|/2+e_{y_i}+\ell_i\\ &\qquad \qquad =|N_i|/2+(\deg(y_i)/2+e_{y_i})-(\deg(z_i)/2+e_{z_i})+\ell_i. \end{align*} $$
$$ \begin{align*} &-|N(z_i)\setminus (\{y_i\}\cup N_i)|/2-e_{z_i}+|N(y_i)\setminus \{z_i\}|/2+e_{y_i}+\ell_i\\ &\qquad \qquad =|N_i|/2-|N(z_i)\setminus \{y_i\}|/2-e_{z_i}+|N(y_i)\setminus \{z_i\}|/2+e_{y_i}+\ell_i\\ &\qquad \qquad =|N_i|/2+(\deg(y_i)/2+e_{y_i})-(\deg(z_i)/2+e_{z_i})+\ell_i. \end{align*} $$
Recalling that
![]() $|(\deg (y_i)/2+e_{y_i})-(\deg (z_i)/2+e_{z_i})|\leq \sqrt {n}$
by property (3) of Lemma 13.1, this means that the quantity on the right-hand side of (13.3) differs from
$|(\deg (y_i)/2+e_{y_i})-(\deg (z_i)/2+e_{z_i})|\leq \sqrt {n}$
by property (3) of Lemma 13.1, this means that the quantity on the right-hand side of (13.3) differs from
![]() $|N_i|/2$
by at most
$|N_i|/2$
by at most
![]() $(2^{D+2}D+1)\sqrt {n}+B\leq 2^{D+3}D\sqrt {n}$
. Now, note that, conditioning on our fixed outcome of
$(2^{D+2}D+1)\sqrt {n}+B\leq 2^{D+3}D\sqrt {n}$
. Now, note that, conditioning on our fixed outcome of
![]() $U\cap W$
, the random variable
$U\cap W$
, the random variable
![]() $\mathbb E[X\,|\,U\setminus \overline {N}]$
is of the form in Lemma 13.6 with the graph
$\mathbb E[X\,|\,U\setminus \overline {N}]$
is of the form in Lemma 13.6 with the graph
![]() $G[N_1\cup \cdots \cup N_S]$
(of size at least
$G[N_1\cup \cdots \cup N_S]$
(of size at least
![]() $\rho \delta \cdot \delta ^{1/\rho }n$
) and with
$\rho \delta \cdot \delta ^{1/\rho }n$
) and with
![]() $R=R(C,H)=\max \{2^{D+3}D,(H+1)/(\rho \delta ^{1+1/\rho })\}$
. This random variable has expected value
$R=R(C,H)=\max \{2^{D+3}D,(H+1)/(\rho \delta ^{1+1/\rho })\}$
. This random variable has expected value
![]() $\mathbb E [X\,|\,U\cap W]$
, which differs from E by at most
$\mathbb E [X\,|\,U\cap W]$
, which differs from E by at most
![]() $2^{s+1}(H+1)n^{3/2}$
by (B). So, by Lemma 13.6(2), with probability at least
$2^{s+1}(H+1)n^{3/2}$
by (B). So, by Lemma 13.6(2), with probability at least
![]() $\Omega _{C,H}(n^{-s/2})$
the outcome of
$\Omega _{C,H}(n^{-s/2})$
the outcome of
![]() $U\setminus \overline {N}$
satisfies both
$U\setminus \overline {N}$
satisfies both
and (13.3) for all
![]() $i=1,\ldots ,s$
(which implies that
$i=1,\ldots ,s$
(which implies that
![]() $\mathcal E_i (y_i,z_i)$
holds for all
$\mathcal E_i (y_i,z_i)$
holds for all
![]() $i=1,\ldots ,s$
). From now on, we condition on such an outcome of
$i=1,\ldots ,s$
). From now on, we condition on such an outcome of
![]() $U\setminus \overline {N}$
.
$U\setminus \overline {N}$
.
Finally, consider the randomness of
![]() $U\cap \overline {N}$
(having conditioned on our outcome of
$U\cap \overline {N}$
(having conditioned on our outcome of
![]() $U\setminus \overline {N}$
). Note that
$U\setminus \overline {N}$
). Note that
![]() $G[\overline {N}]$
is a
$G[\overline {N}]$
is a
![]() $(2C)$
-Ramsey graph (as
$(2C)$
-Ramsey graph (as
![]() $|\overline {N}|\geq \delta ^{1+1/\rho }\cdot n\geq \sqrt {n}$
), and that (in our conditional probability space) X has the form in Theorem 3.1, with expectation
$|\overline {N}|\geq \delta ^{1+1/\rho }\cdot n\geq \sqrt {n}$
), and that (in our conditional probability space) X has the form in Theorem 3.1, with expectation
![]() $\mathbb E[X\,|\, U\setminus \overline {N}]$
. Now, recalling (13.4) and the fact that
$\mathbb E[X\,|\, U\setminus \overline {N}]$
. Now, recalling (13.4) and the fact that
![]() $|x-E|\leq An^{3/2}$
, note that x differs from
$|x-E|\leq An^{3/2}$
, note that x differs from
![]() $\mathbb E[X\,|\, U\setminus \overline {N}]$
by at most
$\mathbb E[X\,|\, U\setminus \overline {N}]$
by at most
![]() $(A+2^{s+1}(H+1)+6R^2) \cdot n^{3/2}$
. Therefore Theorem 3.1 (plugging in
$(A+2^{s+1}(H+1)+6R^2) \cdot n^{3/2}$
. Therefore Theorem 3.1 (plugging in
![]() $(H+1)/\delta ^{1+1/\rho }$
for the ‘H’ and
$(H+1)/\delta ^{1+1/\rho }$
for the ‘H’ and
![]() $(A+2^{s+1}(H+1)+6R^2)/(\delta ^{1+1/\rho })^{3/2}$
for the ‘A’ in Theorem 3.1) implies that (conditioned on our fixed outcome of
$(A+2^{s+1}(H+1)+6R^2)/(\delta ^{1+1/\rho })^{3/2}$
for the ‘A’ in Theorem 3.1) implies that (conditioned on our fixed outcome of
![]() $U\setminus \overline {N}$
and subject only to the randomness of
$U\setminus \overline {N}$
and subject only to the randomness of
![]() $U\cap \overline {N}$
) we have
$U\cap \overline {N}$
) we have
![]() $\Pr [|X-x|\leq B]\gtrsim _{C,H,A} n^{-3/2}$
. This proves (13.2) and thereby gives the desired lower bound for the sum in (13.1).
$\Pr [|X-x|\leq B]\gtrsim _{C,H,A} n^{-3/2}$
. This proves (13.2) and thereby gives the desired lower bound for the sum in (13.1).
Step 2: the upper bound. To establish the desired upper bound
![]() $O_{C,H,A}((|T|/\sqrt {n})^s\cdot n^{-3/2})$
for the sum in (13.1), for each
$O_{C,H,A}((|T|/\sqrt {n})^s\cdot n^{-3/2})$
for the sum in (13.1), for each
![]() $k=0,\ldots ,s$
, we separately consider the contribution of s-tuples
$k=0,\ldots ,s$
, we separately consider the contribution of s-tuples
![]() $((y_1,z_1),\ldots ,(y_s,z_s))\in T^s$
of degeneracy k (see Definition 13.7). By Lemma 13.10, for each
$((y_1,z_1),\ldots ,(y_s,z_s))\in T^s$
of degeneracy k (see Definition 13.7). By Lemma 13.10, for each
![]() $k=0,\ldots ,s$
there are at most
$k=0,\ldots ,s$
there are at most
![]() $|T|^s/\sqrt {n}^k$
different such s-tuples of degeneracy k. Thus, it suffices to prove that for every s-tuple
$|T|^s/\sqrt {n}^k$
different such s-tuples of degeneracy k. Thus, it suffices to prove that for every s-tuple
![]() $((y_1,z_1),\ldots ,(y_s,z_s))\in T^s$
of degeneracy k we have
$((y_1,z_1),\ldots ,(y_s,z_s))\in T^s$
of degeneracy k we have
Recall the definition of the
![]() $s\times n$
matrix
$s\times n$
matrix
![]() $M(y_1,z_1,\ldots ,y_s,z_s)$
in Definition 13.7. For every outcome of
$M(y_1,z_1,\ldots ,y_s,z_s)$
in Definition 13.7. For every outcome of
![]() $U\subseteq V(G)$
, the entries of the vector
$U\subseteq V(G)$
, the entries of the vector
![]() $M(y_1,z_1,\ldots ,y_s,z_s)\vec {1}_U$
are precisely
$M(y_1,z_1,\ldots ,y_s,z_s)\vec {1}_U$
are precisely
![]() $|N(z_i)\cap (U\setminus \{y_i\})|-|N(y_i)\cap (U\setminus \{z_i\})|$
for
$|N(z_i)\cap (U\setminus \{y_i\})|-|N(y_i)\cap (U\setminus \{z_i\})|$
for
![]() $i=1,\ldots ,s$
, since
$i=1,\ldots ,s$
, since
 $$ \begin{align*} \vec{1}_{N(z_i)\setminus \{y_i\}}\cdot \vec{1}_U-\vec{1}_{N(y_i)\setminus \{z_i\}}\cdot \vec{1}_U&=|(N(z_i)\setminus \{y_i\})\cap U|-|(N(y_i)\setminus \{z_i\})\cap U|\\ &=|N(z_i)\cap (U\setminus \{y_i\})|-|N(y_i)\cap (U\setminus \{z_i\})|. \end{align*} $$
$$ \begin{align*} \vec{1}_{N(z_i)\setminus \{y_i\}}\cdot \vec{1}_U-\vec{1}_{N(y_i)\setminus \{z_i\}}\cdot \vec{1}_U&=|(N(z_i)\setminus \{y_i\})\cap U|-|(N(y_i)\setminus \{z_i\})\cap U|\\ &=|N(z_i)\cap (U\setminus \{y_i\})|-|N(y_i)\cap (U\setminus \{z_i\})|. \end{align*} $$
So if the events
![]() $\mathcal {E}_i(y_{i},z_{i})$
for
$\mathcal {E}_i(y_{i},z_{i})$
for
![]() $i=1,\ldots ,s$
hold, we must have
$i=1,\ldots ,s$
hold, we must have
![]() $M(y_1,z_1,\ldots ,y_s,z_s)\vec {1}_U=(e_{y_i}-e_{z_i}+\ell _i)_{i=1}^s$
. Since
$M(y_1,z_1,\ldots ,y_s,z_s)\vec {1}_U=(e_{y_i}-e_{z_i}+\ell _i)_{i=1}^s$
. Since
![]() $((y_1,z_1),\ldots ,(y_s,z_s))$
is not
$((y_1,z_1),\ldots ,(y_s,z_s))$
is not
![]() $(k+1)$
-degenerate, whenever we delete
$(k+1)$
-degenerate, whenever we delete
![]() $\delta ^{3/\gamma }\cdot n$
columns of the matrix
$\delta ^{3/\gamma }\cdot n$
columns of the matrix
![]() $M(y_1,z_1,\ldots ,y_s,z_s)$
the resulting matrix still has rank at least
$M(y_1,z_1,\ldots ,y_s,z_s)$
the resulting matrix still has rank at least
![]() $s-k$
. So applying Theorem 13.8 (with
$s-k$
. So applying Theorem 13.8 (with
![]() $\lambda =\delta ^{3/\rho }$
and
$\lambda =\delta ^{3/\rho }$
and
![]() $r=s-k$
) yields:
$r=s-k$
) yields:
Thus, in order to show (13.5), it now suffices to prove the conditional probability bound
Note that the events
![]() $\mathcal {E}_i(y_{i},z_{i})$
for
$\mathcal {E}_i(y_{i},z_{i})$
for
![]() $i=1,\ldots ,s$
only depend on
$i=1,\ldots ,s$
only depend on
![]() $U\cap (V(G)\setminus \overline {N}(y_1,z_1,\ldots ,y_s,z_s))$
. So, condition on any outcome of
$U\cap (V(G)\setminus \overline {N}(y_1,z_1,\ldots ,y_s,z_s))$
. So, condition on any outcome of
![]() $U\cap (V(G)\setminus \overline {N}(y_1,z_1,\ldots ,y_s,z_s))$
such that
$U\cap (V(G)\setminus \overline {N}(y_1,z_1,\ldots ,y_s,z_s))$
such that
![]() $\mathcal {E}_i(y_{i},z_{i})$
holds for
$\mathcal {E}_i(y_{i},z_{i})$
holds for
![]() $i=1,\ldots ,s$
. Subject to the randomness of
$i=1,\ldots ,s$
. Subject to the randomness of
![]() $U\cap \overline {N}(y_1,z_1,\ldots ,y_s,z_s)$
, our random variable X has the form in Theorem 3.1, with the graph
$U\cap \overline {N}(y_1,z_1,\ldots ,y_s,z_s)$
, our random variable X has the form in Theorem 3.1, with the graph
![]() $G[\overline {N}(y_1,z_1,\ldots ,y_s,z_s)]$
(which is a
$G[\overline {N}(y_1,z_1,\ldots ,y_s,z_s)]$
(which is a
![]() $(2C)$
-Ramsey graph, since
$(2C)$
-Ramsey graph, since
![]() $|\overline {N}(y_1,z_1,\ldots ,y_s,z_s)|\geq \delta |S_0|\geq \delta ^{1+1/\rho }\cdot n\geq \sqrt {n}$
by property (2) of Lemma 13.1). Thus, in our conditional probability space, Theorem 3.1 (plugging in
$|\overline {N}(y_1,z_1,\ldots ,y_s,z_s)|\geq \delta |S_0|\geq \delta ^{1+1/\rho }\cdot n\geq \sqrt {n}$
by property (2) of Lemma 13.1). Thus, in our conditional probability space, Theorem 3.1 (plugging in
![]() $(H+1)\delta ^{-1-1/\rho }$
for the ‘H’ in Theorem 3.1) yields
$(H+1)\delta ^{-1-1/\rho }$
for the ‘H’ in Theorem 3.1) yields
This proves (13.6) and therefore establishes (13.5), as desired.
Acknowledgements
We thank Jacob Fox for comments motivating the inclusion of Remark 1.3, and Zach Hunter for pointing out several minor corrections to the manuscript. We also thank the two anonymous referees for carefully reading the manuscript and many helpful comments.
Competing interest
The authors have no competing interest to declare.
Financial support
Kwan was supported for part of this work by ERC Starting Grant ‘RANDSTRUCT’ No. 101076777. Sah and Sawhney were supported by NSF Graduate Research Fellowship Program DGE-2141064. Sah was supported by the PD Soros Fellowship. Sauermann was supported by NSF Award DMS-2100157, and for part of this work by a Sloan Research Fellowship.