No CrossRef data available.
Article contents
Khintchine-type double recurrence in abelian groups
Published online by Cambridge University Press: 24 April 2024
Abstract
We prove a Khintchine-type recurrence theorem for pairs of endomorphisms of a countable discrete abelian group. As a special case of the main result, if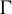 
$\Gamma $ is a countable discrete abelian group, 
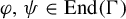$\varphi , \psi \in \mathrm {End}(\Gamma )$, and 
$\psi - \varphi $ is an injective endomorphism with finite index image, then for any ergodic measure-preserving 
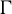$\Gamma $-system 
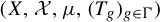$( X, {\mathcal {X}}, \mu , (T_g)_{g \in \Gamma } )$, any measurable set 
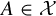$A \in {\mathcal {X}}$, and any 
${\varepsilon }> 0$, there is a syndetic set of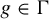 
$g \in \Gamma$ such that 
$\mu ( A \cap T_{\varphi(g)}^{-1} A \cap T_{\psi(g)}^{-1} A ) > \mu(A)^3 - \varepsilon$. This generalizes the main results of Ackelsberg et al [Khintchine-type recurrence for 3-point configurations. Forum Math. Sigma 10 (2022), Paper no. e107] and essentially answers a question left open in that paper [Question 1.12; Khintchine-type recurrence for 3-point configurations. Forum Math. Sigma 10 (2022), Paper no. e107]. For the group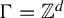 
$\Gamma = {\mathbb {Z}}^d$, the result applies to pairs of endomorphisms given by matrices whose difference is non-singular. The key ingredients in the proof are: (1) a recent result obtained jointly with Bergelson and Shalom [Khintchine-type recurrence for 3-point configurations. Forum Math. Sigma 10 (2022), Paper no. e107] that says that the relevant ergodic averages are controlled by a characteristic factor closely related to the quasi-affine (or Conze–Lesigne) factor; (2) an extension trick to reduce to systems with well-behaved (with respect to 
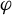$\varphi $ and 
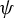$\psi $) discrete spectrum; and (3) a description of Mackey groups associated to quasi-affine cocycles over rotational systems with well-behaved discrete spectrum.
MSC classification
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press
References
Ackelsberg, E., Bergelson, V. and Best, A.. Multiple recurrence and large intersections for abelian group actions. Discrete Anal. (2021), Paper no. 18.Google Scholar
Ackelsberg, E., Bergelson, V. and Shalom, O.. Khintchine-type recurrence for 3-point configurations. Forum Math. Sigma 10 (2022), Paper no. e107.CrossRefGoogle Scholar
Austin, T.. Non-conventional ergodic averages for several commuting actions of an amenable group. J. Anal. Math. 130 (2016), 243–274.CrossRefGoogle Scholar
Behrend, F. A.. On sets of integers which contain no three terms in arithmetical progression. Proc. Natl. Acad. Sci. USA 32 (1946), 331–332.CrossRefGoogle ScholarPubMed
Bergelson, V. and Ferré Moragues, A.. An ergodic correspondence principle, invariant means and applications. Israel J. Math. 245(2) (2021), 921–962.CrossRefGoogle Scholar
Bergelson, V., Host, B. and Kra, B.. Multiple recurrence and nilsequences. Invent. Math. 160(2) (2005), 261–303, appendix by I. Ruzsa.CrossRefGoogle Scholar
Bergelson, V. and Leibman, A.. Cubic averages and large intersections. Recent Trends in Ergodic Theory and Dynamical Systems. Ed. S. Bhattacharya, T. Das, A. Ghosh and R. Shah. American Mathematical Society, Providence, RI, 2015, pp. 5–19.Google Scholar
Bergelson, V., Tao, T. and Ziegler, T.. An inverse theorem for the uniformity seminorms associated with the action of
${F}_p^{\infty }$
. Geom. Funct. Anal. 19(6) (2010), 1539–1596.CrossRefGoogle Scholar
${F}_p^{\infty }$
. Geom. Funct. Anal. 19(6) (2010), 1539–1596.CrossRefGoogle ScholarBergelson, V., Tao, T. and Ziegler, T.. Multiple recurrence and convergence results associated to
${F}_p^{\omega }$
-actions. J. Anal. Math. 127 (2015), 329–378.CrossRefGoogle Scholar
${F}_p^{\omega }$
-actions. J. Anal. Math. 127 (2015), 329–378.CrossRefGoogle ScholarBerger, A., Sah, A., Sawhney, M. and Tidor, J.. Popular differences for matrix patterns. Trans. Amer. Math. Soc. 375(4) (2022), 2677–2704.CrossRefGoogle Scholar
Chu, Q.. Multiple recurrence for two commuting transformations. Ergod. Th. & Dynam. Sys. 31(3) (2011), 771–792.CrossRefGoogle Scholar
Furstenberg, H.. Ergodic behavior of diagonal measures and a theorem of Szemerédi on arithmetic progressions. J. Anal. Math. 31 (1977), 204–256.CrossRefGoogle Scholar
Furstenberg, H. and Katznelson, Y.. An ergodic Szemerédi theorem for IP-systems and combinatorial theory. J. Anal. Math. 45 (1985), 117–168.CrossRefGoogle Scholar
Furstenberg, H. and Weiss, B.. A mean ergodic theorem for
$\frac{1}{N}\sum_{n=1}^Nf({T}^n(x))g({T}^{n^2}(x))$
. Convergence in Ergodic Theory and Probability, Columbus, OH 1993 (Ohio State University Mathematical Research Institute Publications, 5). Ed. V. Bergelson, P. March and J. Rosenblatt. de Gruyter, Berlin, 1996), pp. 193–227.Google Scholar
$\frac{1}{N}\sum_{n=1}^Nf({T}^n(x))g({T}^{n^2}(x))$
. Convergence in Ergodic Theory and Probability, Columbus, OH 1993 (Ohio State University Mathematical Research Institute Publications, 5). Ed. V. Bergelson, P. March and J. Rosenblatt. de Gruyter, Berlin, 1996), pp. 193–227.Google ScholarGlasner, E.. Ergodic Theory via Joinings (Mathematical Surveys and Monographs, 101). American Mathematical Society, Providence, RI, 2003).CrossRefGoogle Scholar
Gowers, W. T.. A new proof of Szemeredi’s theorem. Geom. Funct. Anal. 11(3) (2001), 465–588.CrossRefGoogle Scholar
Green, B.. A Szemerédi-type regularity lemma in abelian groups, with applications. Geom. Funct. Anal. 15(2) (2005), 340–376.CrossRefGoogle Scholar
Green, B.. Montréal notes on quadratic Fourier analysis. Additive Combinatorics (CRM Proceedings and Lecture Notes, 43). Ed. A. Granville, M. B. Nathanson and J. Solymosi. American Mathematical Society, Providence, RI, 2007, pp. 69–102.CrossRefGoogle Scholar
Green, B. and Tao, T.. An arithmetic regularity lemma, an associated counting lemma, and applications. An Irregular Mind (Bolyai Society Mathematical Studies, 21). Ed. I. Bárány, J. Solymosi and G. Sági. János Bolyai Mathematical Society, Budapest, 2010, pp. 261–334.CrossRefGoogle Scholar
Griesmer, J. T.. Ergodic averages, correlation sequences, and sumsets. PhD Thesis, The Ohio State University, 2009.Google Scholar
Griesmer, J. T., Le, A. N. and Lê, T. H.. Bohr sets in sumsets II: countable abelian groups. Forum Math. Sigma 11 (2023), Paper no. e57.CrossRefGoogle Scholar
Host, B. and Kra, B.. Convergence of Conze–Lesigne averages. Ergod. Th. & Dynam. Sys. 21(2) (2001), 493–509.CrossRefGoogle Scholar
Host, B. and Kra, B.. Nonconventional ergodic averages and nilmanifolds. Ann. of Math. (2) 161(1) (2005), 397–488.CrossRefGoogle Scholar
Khintchine, A.. Eine Verschärfung des Poincaréschen “Wiederkehrsatzes”. Compos. Math. 1 (1935), 177–179.Google Scholar
Kovač, V.. Popular differences for right isosceles triangles. Electron. J. Combin. 28 (2021), Paper no. 4.27.CrossRefGoogle Scholar
Le, A. N. and Lê, T. H.. Bohr sets in sumsets I: compact groups. Preprint, 2021, arXiv:2112.11997.Google Scholar
Lesigne, E.. Équations fonctionnelles, couplages de produits gauches et théorèmes ergodiques pour mesures diagonales. Bull. Soc. Math. France 121(3) (1993), 315–351.CrossRefGoogle Scholar
Pilatte, C.. New bound for Roth’s theorem with generalized coefficients. Discrete Anal. (2022), Paper no. 16.Google Scholar
Prendiville, S.. Matrix progressions in multidimensional sets of integers. Mathematika 61(1) (2015), 14–48.CrossRefGoogle Scholar
Rudin, W.. Fourier Analysis on Groups (Wiley Classics Library). John Wiley & Sons, Inc., New York, 1990.CrossRefGoogle Scholar
Shalom, O.. Multiple ergodic averages in abelian groups and Khintchine type recurrence. Trans. Amer. Math. Soc. 375(4) (2022), 2729–2761.Google Scholar
Srivastava, S. M.. A Course on Borel Sets (Graduate Texts in Mathematics, 180). Springer-Verlag, New York, 1998.CrossRefGoogle Scholar