Hostname: page-component-848d4c4894-wzw2p Total loading time: 0 Render date: 2024-05-23T15:08:35.205Z Has data issue: false hasContentIssue false
  • English
  • Français

Approximate discrete entropy monotonicity for log-concave sums

Part of: Communication, information Distribution theory - Probability

Published online by Cambridge University Press:  13 November 2023

Lampros Gavalakis Open the ORCID record for Lampros Gavalakis [Opens in a new window]
Lampros Gavalakis*
Affiliation:
Laboratoire d’Analyse et de Mathématiques Appliquées, Université Gustave Eiffel, Champs-sur-Marne, France
*
Email: lampros.gavalakis@univ-eiffel.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

It is proven that a conjecture of Tao (2010) holds true for log-concave random variables on the integers: For every 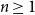$n \geq 1$, if 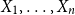$X_1,\ldots,X_n$ are i.i.d. integer-valued, log-concave random variables, then

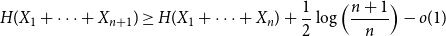\begin{equation*} H(X_1+\cdots +X_{n+1}) \geq H(X_1+\cdots +X_{n}) + \frac {1}{2}\log {\Bigl (\frac {n+1}{n}\Bigr )} - o(1) \end{equation*}
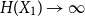as $H(X_1) \to \infty$, where 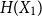$H(X_1)$ denotes the (discrete) Shannon entropy. The problem is reduced to the continuous setting by showing that if 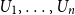$U_1,\ldots,U_n$ are independent continuous uniforms on $(0,1)$, then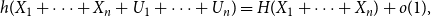
\begin{equation*} h(X_1+\cdots +X_n + U_1+\cdots +U_n) = H(X_1+\cdots +X_n) + o(1), \end{equation*}
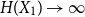as $H(X_1) \to \infty$, where $h$ stands for the differential entropy. Explicit bounds for the 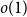$o(1)$-terms are provided.

Keywords

Entropymonotonicitylog-concavityentropy power inequalitycentral limit theoremconcentrationsumset inequalities

MSC classification

Primary: 94A17: Measures of information, entropy
Secondary: 60E15: Inequalities; stochastic orderings 39B62: Functional inequalities, including subadditivity, convexity, etc.
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 33 , Issue 2 , March 2024 , pp. 196 - 209
Copyright
© The Author(s), 2023. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

L.G. has received funding from the European Union’s Horizon 2020 research and innovation program under the Marie Sklodowska-Curie grant agreement No 101034255.

References

Artstein, S., Ball, K., Barthe, F. and Naor, A. (2004) Solution of Shannon’s problem on the monotonicity of entropy. J. Am. Math. Soc. 17(4) 975–982.CrossRefGoogle Scholar
Barron, A. R. (1986) Entropy and the central limit theorem, Ann. Prob. 14, 336–342.CrossRefGoogle Scholar
Bobkov, S. G., Marsiglietti, A. and Melbourne, J. (2022) Concentration functions and entropy bounds for discrete log-concave distributions. Comb. Prob. Comput. 31(1) 54–72.CrossRefGoogle Scholar
Cover, T. M. and Thomas, J. A. (2006) Elements of Information Theory. Wiley-Interscience, New York, NY, USA, Wiley Series in Telecommunications and Signal Processing .Google Scholar
Davis, B. and McDonald, D. (1995) An elementary proof of the local central limit theorem. J. Theor. Probab. 8(3) 693–701.CrossRefGoogle Scholar
Gavalakis, L. and Kontoyiannis, I. (2021) Entropy and the discrete central limit theorem, arXiv preprint arXiv: 2106.00514.Google Scholar
Haghighatshoar, S., Abbe, E. and Telatar, E. (2012) Adaptive sensing using deterministic partial Hadamard matrices. IEEE, pp. 1842–1846, In 2012 IEEE International Symposium on Information Theory Proceedings.CrossRefGoogle Scholar
Haghighatshoar, S., Abbe, E. and Telatar, I. E. (2014) A new entropy power inequality for integer-valued random variables. IEEE Trans. Inform. Theory 60(7) 3787–3796.CrossRefGoogle Scholar
Harremoés, P. and Vignat, C. (2003) An entropy power inequality for the binomial family. JIPAM. J. Inequal. Pure Appl. Math. 4(5) 93.Google Scholar
Hoggar, S. (1974) Chromatic polynomials and logarithmic concavity. J. Comb. Theory, Ser. B 16(3) 248–254.CrossRefGoogle Scholar
Madiman, M. and Barron, A. (2007) Generalized entropy power inequalities and monotonicity properties of information. IEEE Trans. Inform. Theory 53(7) 2317–2329.CrossRefGoogle Scholar
McDonald, D. R. (1980) On local limit theorem for integer-valued random variables. Theory Prob. Appl. 24(3) 613–619.CrossRefGoogle Scholar
Mineka, J. (1973) A criterion for tail events for sums of independent random variables. Z. für Wahrscheinlichkeitstheorie und Verw. Gebiete 25(3) 163–170.CrossRefGoogle Scholar
Ruzsa, I. Z. (2009) Sumsets and entropy. Random Struct. Algorithms 34(1) 1–10.CrossRefGoogle Scholar
Shannon, C. E. (1948) A mathematical theory of communication. Bell Syst. Tech. J. 27(3) 379–423.CrossRefGoogle Scholar
Stam, A. J. (1959) Some inequalities satisfied by the quantities of information of Fisher and Shannon. Inf. Control 2(2) 101–112.CrossRefGoogle Scholar
Tao, T. (2010) Sumset and inverse sumset theory for Shannon entropy. Comb. Probab. Comput. 19(4) 603–639.CrossRefGoogle Scholar
Tao, T. and Vu, V. H. (2005) Entropy methods [Online]. Available: http://www.math.ucla.edu/~tao/preprints/Expository/.Google Scholar
Tao, T. and Vu, V. H. (2006) Additive Combinatorics. Cambridge University Press, Cambridge Studies in Advanced Mathematics.CrossRefGoogle Scholar
Woo, J. O. and Madiman, M. (2015) A discrete entropy power inequality for uniform distributions. IEEE, pp. 1625–1629. In 2015 IEEE International Symposium on Information Theory (ISIT).CrossRefGoogle Scholar