Hostname: page-component-848d4c4894-nr4z6 Total loading time: 0 Render date: 2024-06-02T12:56:45.141Z Has data issue: false hasContentIssue false
  • English
  • Français

A Note on a Square Type Functional Equation

Published online by Cambridge University Press:  20 November 2018

Shigeru Haruki
Shigeru Haruki*
Affiliation:
University of Waterloo, Waterloo Ontario
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The following square functional equation

(1)

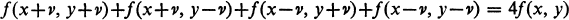
was considered (for example [l]-[9]) previously.

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 16 , Issue 3 , September 1973 , pp. 443 - 445
Copyright
Copyright © Canadian Mathematical Society 1973

References

1. McKiernan, M. A., Boundedness on a set of positive measure and the mean value property characterizes polynomials on a space Vn , Aequationes Math. 4 (1970), 31-36.Google Scholar
2. McKiernan, M. A., On Haruki's functional equation, Aequationes Math. 1 (1968), p. 143.Google Scholar
3. McKiernan, M. A., Difference and mean value type functional equations, C.I.M.E., Roma, (1971), 259-286.Google Scholar
4. Aczél, J., Haruki, H., McKiernan, M. A., and Sakovic, G. N., General and regular solutions of functional equations characterizing harmonic polynomials, Aequationes Math. 1 (1968), 37-53.Google Scholar
5. Šwiatak, H., On the regularity of the distributional and continuous solutions of the functional equations , Aequationes Math. 1 (1968), 6-19.Google Scholar
6. Šwiatak, H., A generalization of the Haruki functional equation, Ann. Polon. Math. 22 (1970), 370-376.Google Scholar
7. Šwiatak, H., On some applications of the theory of distributions in functional equations, Prace Mat. 14 (1970), 35-36.Google Scholar
8. Haruki, H., On a relation between the "square" functional equation and the "square" meanvalue property, Canad. Math. Bull. (2) 14 (1971), 161-165.Google Scholar
9. Haruki, H., On an application of the "square" functional equation to a geometric characterization of quadratic functions from the standpoint of conformal-mapping properties, Aequationes Math. 6 (1971), 36-38.Google Scholar
10. Haruki, S., A note on a Pentomino functional equation, Ann. Polon. Math., (to appear).Google Scholar