No CrossRef data available.
Article contents
Almost sure convergence of the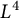 
$L^4$ norm of Littlewood polynomials
Published online by Cambridge University Press: 15 March 2024
Abstract
This paper concerns the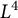 
$L^4$ norm of Littlewood polynomials on the unit circle which are given by i.e., they have random coefficients in 
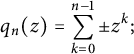$$ \begin{align*}q_n(z)=\sum_{k=0}^{n-1}\pm z^k;\end{align*} $$
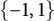$\{-1,1\}$. Let We show that 
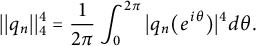$$ \begin{align*}||q_n||_4^4=\frac{1}{2\pi}\int_0^{2\pi}|q_n(e^{i\theta})|^4 d\theta.\end{align*} $$
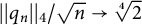$||q_n||_4/\sqrt {n}\rightarrow \sqrt [4]{2}$ almost surely as 
$n\to \infty $. This improves a result of Borwein and Lockhart (2001, Proceedings of the American Mathematical Society 129, 1463–1472), who proved the corresponding convergence in probability. Computer-generated numerical evidence for the a.s. convergence has been provided by Robinson (1997, Polynomials with plus or minus one coefficients: growth properties on the unit circle, M.Sc. thesis, Simon Fraser University). We indeed present two proofs of the main result. The second proof extends to cases where we only need to assume a fourth moment condition.
MSC classification
- Type
- Article
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press on behalf of Canadian Mathematical Society
Footnotes
Y. Duan is supported by the NNSF of China (Grant No. 12171075) and the Science and Technology Research Project of Education Department of Jilin Province (Grant No. JJKH20241406KJ). X. Fang is supported by the NSTC of Taiwan (Grant No. 112-2115-M-008-010-MY2).
References
Balister, P., Bollobás, B., Morris, R., Sahasrabudhe, J., and Tiba, M.,
Flat Littlewood polynomials exist
. Ann. Math. 192(2020), 977–1004.CrossRefGoogle Scholar
Beck, J.,
Flat polynomials on the unit circle – note on a problem of Littlewood
. Bull. Lond. Math. Soc. 23(1991), 269–277.CrossRefGoogle Scholar
Beenker, G. F. M., Claasen, T. A. C. M., and Hermens, P. W. C.,
Binary sequences with a maximally flat amplitude spectrum
. Philips J. Res. 40(1985), 289–304.Google Scholar
Bernasconi, J.,
Low autocorrelation binary sequences: statistical mechanics and configuration state analysis
. J. Physique 48(1987), 559–567.CrossRefGoogle Scholar
Borwein, P., Computational excursions in analysis and number theory, CMB Books in Mathematics, 10, Springer, New York, 2002.CrossRefGoogle Scholar
Borwein, P., Choi, K.-K. S., and Jedwab, J.,
Binary sequences with merit factor greater than 6.34
. IEEE Trans. Inform. Theory 50(2004), 3234–3249.CrossRefGoogle Scholar
Borwein, P. and Lockhart, R., The expected
${L}_p$
norm of random polynomials. Proc. Amer. Math. Soc. 129(2001), 1463–1472.CrossRefGoogle Scholar
${L}_p$
norm of random polynomials. Proc. Amer. Math. Soc. 129(2001), 1463–1472.CrossRefGoogle ScholarBorwein, P. and Mossinghoff, M., Rudin–Shapiro-like polynomials in
${L}_4$
. Math. Comput. 69(2000), 1157–1166.CrossRefGoogle Scholar
${L}_4$
. Math. Comput. 69(2000), 1157–1166.CrossRefGoogle ScholarCinlar, E., Probability and stochastics, Graduate Texts in Mathematics, 261, Springer, New York, 2011.CrossRefGoogle Scholar
Erdős, P.,
An inequality for the maximum of trigonometric polynomials
. Ann. Polon. Math. 12(1962), 151–154.CrossRefGoogle Scholar
Golay, M. J. E.,
The merit factor of Legendre sequences
. IEEE Trans. Inform. Theory 29(1983), 934–936.CrossRefGoogle Scholar
Halász, G.,
On a result of Salem and Zygmund concerning random polynomials
. Stud. Sci. Math. Hung. 8(1973), 369–377.Google Scholar
Høholdt, T. and Jensen, H. E.,
Determination of the merit factor of Legendre sequences
. IEEE Trans. Inform. Theory 34(1988), 161–164.CrossRefGoogle Scholar
Jedwab, J.,
A survey of the merit factor problem for binary sequences
. In: Helleseth, T., Sarwate, D., Song, H.-Y., and Yang, K. (eds.), Sequences and their applications-SETA 2004, Lecture Notes in Computer Science, 3486, Springer, New York, 2005, pp. 30–55.CrossRefGoogle Scholar
Jedwab, J., Katz, D. J., and Schmidt, K.-U., Littlewood polynomials with small
${L}^4$
norm. Adv. Math. 241(2013), 127–136.CrossRefGoogle Scholar
${L}^4$
norm. Adv. Math. 241(2013), 127–136.CrossRefGoogle ScholarJensen, J. M., Jensen, H. E., and Høholdt, T.,
The merit factor of binary sequences related to difference sets
. IEEE Trans. Inform. Theory 37(1991), 617–626.CrossRefGoogle Scholar
Kahane, J.-P.,
Sur les polynômes á coefficients unimodulaires
. Bull. Lond. Math. Soc. 12(1980), 321–342.CrossRefGoogle Scholar
Kahane, J.-P., Some random series of functions, 2nd ed., Cambridge Studies in Advanced Mathematics, 5, Cambridge University Press, Cambridge, 1985.Google Scholar
Littlewood, J. E., On polynomials
$\sum \limits^n\pm {z}^m$
and
$\sum \limits^n{e}^{\alpha_mi}{z}^m$
,
$z={e}^{\theta i}$
. J. Lond. Math. Soc. 41(1966), 367–376.CrossRefGoogle Scholar
$\sum \limits^n\pm {z}^m$
and
$\sum \limits^n{e}^{\alpha_mi}{z}^m$
,
$z={e}^{\theta i}$
. J. Lond. Math. Soc. 41(1966), 367–376.CrossRefGoogle ScholarLittlewood, J. E., Some problems in real and complex analysis, Heath Mathematical Monographs, D. C. Heath, Lexington, MA, 1968.Google Scholar
Montgomery, H. L.,
Littlewood polynomials
. In: Analytic number theory, modular forms and q-hypergeometric series. Springer Proceedings in Mathematics and Statistics, 221, Springer, Cham, 2017, pp. 533–553.CrossRefGoogle Scholar
Newman, D. J. and Byrnes, J. S., The
${L}^4$
norm of a polynomial with coefficients
$\pm 1$
. Amer. Math. Mon. 97(1990), 42–45.Google Scholar
${L}^4$
norm of a polynomial with coefficients
$\pm 1$
. Amer. Math. Mon. 97(1990), 42–45.Google ScholarRobinson, L., Polynomials with plus or minus one coefficients: growth properties on the unit circle. M.Sc. thesis, Simon Fraser University, 1997.Google Scholar
Salem, R. and Zygmund, A.,
Some properties of trigonometric series whose terms have random signs
. Acta Math. 91(1954), 254–301.CrossRefGoogle Scholar