Hostname: page-component-848d4c4894-m9kch Total loading time: 0 Render date: 2024-06-02T17:42:55.196Z Has data issue: false hasContentIssue false
  • English
  • Français

SL(2,5) and Frobenius Galois Groups Over Q

Published online by Cambridge University Press:  20 November 2018

Jack Sonn
Jack Sonn*
Affiliation:
Technion, Israeli Institute of Technology, Haifa, Israel
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A finite transitive permutation group G is called a Frobenius group if every element of G other than 1 leaves at most one letter fixed, and some element of G other than 1 leaves some letter fixed. It is proved in [20] (and sketched below) that if k is a number field such that SL(2, 5) and one other nonsolvable group Ŝ5 of order 240 are realizable as Galois groups over k, then every Frobenius group is realizable over k. 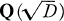It was also proved in [20] that there exists a quadratic (imaginary) field over which these two groups are realizable. In this paper we prove that they are realizable over the rationals Q, hence we Obtain

THEOREM 1. Every Frobenius group is realizable as the Galois group of an extension of the rational numbersQ.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 32 , Issue 2 , February 1980 , pp. 281 - 293
Copyright
Copyright © Canadian Mathematical Society 1980

References

1. Gillard, R., Plongement d'une extension d'ordre p ou p2 dans une surextension non abelienne d'ordre p\ J.R. Ang. Math. 268/269 (1974), 418–426.Google Scholar
2. Gordon, B. and Schacher, M., Quartic coverings of a cubic, J. Number Th. (to appear).Google Scholar
3. Gordon, B. and Schacher, M., The admissibility of A5 , J. Number Th. (to appear).Google Scholar
4. Gruenberg, K. W., Cohomological topics in group theory, Lecture Notes, Springer-Verlag (1970).Google Scholar
5. Hoechsmann, K., Zum Einbettungsproblem, J.R. Ang. Math. 220 (1968), 81–100.Google Scholar
6. Hunter, J., The minimum discriminants of quintic fields, Proc. Glasgow Math. Assoc. 3 (1956), 57–67.Google Scholar
7. Huppert, B., Endliche Gruppen I, Springer-Verlag (1967).Google Scholar
8. Jehne, W., Uber die Einheiten-und Divisorenklassengruppe von reelen Frobeniuskôrpern von Maximaltyp, Math. Z. 152 (1976), 223–252.Google Scholar
9. McCulloh, L. R., Frobenius groups and integral bases, J.R. Ang. Math. 248 (1971), 123–126.Google Scholar
10. Neukirch, J., Uber das Einbettungsproblem der algebraischen Zahlentheorie, Inv. Math. 21 (1973), 59–116.Google Scholar
11. Passman, D., Permutation groups (Benjamin, N.Y., 1968).Google Scholar
12. Pôlya, G. and Szegô, G., Problems and theorems in analysis, Vol. II, Springer-Verlag (1976).Google Scholar
13. Schacher, M., Subfields of division rings, I, J. Alg. 9 (1968), 451–477.Google Scholar
14. Scholz, A., Uber die Bildung algebraischer Zahlkôper mit auflôsbarer Galoissche Gruppe, Math Z. 30 (1929), 332–356.Google Scholar
15. Schur, J., Affectlose Gleichungen in der Théorie der Laguerreschen und Hermiteschen Polynôme, J.f.R. Ang. Math. 165 (1931), 52–58.Google Scholar
16. Serre, J. P., Cohomologie galoisienne, Lecture Notes, Springer-Verlag (1965).Google Scholar
17. Shafarevich, I. R., On the problem of imbedding fields, Transi. A.M.S., Ser. 2. 4 (1956), 151–183.Google Scholar
18. Shafarevich, I. R., Construction of fields of algebraic numbers with given solvable Galois group, Transi. A.M.S., Ser. 2. 4 (1956), 185–237.Google Scholar
19. Sonn, J., On the embedding problem for nonsolvable Galois groups of algebraic number fields: reduction theorems, J. Number Th. 4 (1972), 411–436.Google Scholar
20. Sonn, J., Frobenius Galois groups over quadratic fields, Israel J. Math. 31 (1978), 91–96.Google Scholar
21. Tate, J. T., Global class field theory, in Algebraic number theory, Ed. Cassels, J. W. S. and Frohlich, A., Thompson (1967).Google Scholar
22. Weiss, E., Algebraic number theory, McGraw-Hill (1963).Google Scholar