Hostname: page-component-848d4c4894-ttngx Total loading time: 0 Render date: 2024-05-19T18:51:11.130Z Has data issue: false hasContentIssue false
  • English
  • Français

Existence and symmetry breaking results for positive solutions of elliptic Hamiltonian systems

Part of: Elliptic equations and systems Partial differential equations

Published online by Cambridge University Press:  24 April 2024

Abbas Moameni  and
Kok Lin Wong
Abbas Moameni*
Affiliation:
School of Mathematics and Statistics, Carleton University, Ottawa, ON, Canada e-mail: KelseeWong@cmail.carleton.ca
Kok Lin Wong
Affiliation:
School of Mathematics and Statistics, Carleton University, Ottawa, ON, Canada e-mail: KelseeWong@cmail.carleton.ca
*
e-mail: momeni@math.carleton.ca
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we are interested in positive solutions of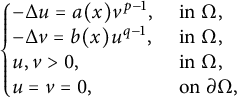

$$ \begin{align*}\left\{ \begin{array}{@{}ll} -\Delta u = a(x)v^{p-1}, \quad &\text{ in } \Omega,\\ -\Delta v = b(x)u^{q-1}, \quad &\text{ in } \Omega,\\ u,v>0, \quad &\text{ in } \Omega,\\ u=v=0, \quad &\text{ on } \partial\Omega, \end{array} \right. \end{align*} $$
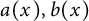where $\Omega $ is a bounded annular domain (not necessarily an annulus) in ${\mathbb {R}}^N (N \ge 3)$ and $ a(x), b(x)$ are positive continuous functions. We show the existence of a positive solution for a range of supercritical values of p and q when the problem enjoys certain mild symmetry and monotonicity conditions. We shall also address the symmetry breaking phenomena where the system is fully symmetric. Indeed, as a consequence of our results, we shall show that problem (1) has 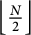$\Bigl \lfloor \frac {N}{2} \Bigr \rfloor $ (the floor of $\frac {N}{2}$) positive non-radial solutions when $ a(x)=b(x)=1$ and $\Omega $ is an annulus with certain assumptions on the radii. In general, for the radial case where the domain is an annulus, we prove the existence of a non-radial solution provided
$$ \begin{align*}(p-1)(q-1)> \Big(1+\frac{2N}{\lambda_H}\Big)^2\left(\frac{q}{p}\right),\end{align*} $$
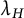where $\lambda _H$ is the best constant for the Hardy inequality on 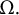$\Omega .$ We remark that the best constant $\lambda _H$ for the Hardy inequality is just the characteristic of the domain, and is independent of the choices of p and 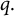$q.$ For this reason, the aforementioned inequality plays a major role to prove the existence and multiplicity of non-radial solutions when the problem is fully symmetric. Our proofs use a variational formulation on appropriate convex subsets for which the lack of compactness is recovered for the supercritical problem.

Keywords

Symmetry breakingHamiltonian systemsvariational principles

MSC classification

Primary: 35B06: Symmetries, invariants, etc. 35J50: Variational methods for elliptic systems 35J57: Boundary value problems for second-order elliptic systems
Type
Article
Information
Canadian Journal of Mathematics , First View , pp. 1 - 29
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

A.M. is pleased to acknowledge the support of the National Sciences and Engineering Research Council of Canada.

References

Bonheure, D., Moreira dos Santos, E., and Ramos, M., Symmetry and symmetry breaking for ground state solutions of some strongly coupled elliptic systems . J. Funct. Anal. 264(2013), no. 1, 62–96.CrossRefGoogle Scholar
Bonheure, D., Moreira dos Santos, E., Ramos, M., and Tavares, H., Existence and symmetry of least energy nodal solutions for Hamiltonian elliptic systems . J. Math. Pures Appl. (9) 104(2015), no. 6, 1075–1107.CrossRefGoogle Scholar
Bonheure, D., Moreira dos Santos, E., and Tavares, H., Hamiltonian elliptic systems: A guide to variational frameworks . Port. Math. 71(2014), nos. 3–4, 301–395.CrossRefGoogle Scholar
Cabré, X. and Ros-Oton, X., Regularity of stable solutions up to dimension 7 in domains of double revolution . Comm. Partial Differential Equations 38(2013), no. 1, 135–154.CrossRefGoogle Scholar
Calanchi, M. and Ruf, B., Radial and non radial solutions for Hardy–Hénon type elliptic systems . Calc. Var. Partial Differential Equations 38(2010), nos. 1–2, 111–133.CrossRefGoogle Scholar
Cardoso, J. A., do, J. M., and Medeiros, Ó. E., Hamiltonian elliptic systems with nonlinearities of arbitrary growth . Topol. Methods Nonlinear Anal. 47(2016), no. 2, 593–612.Google Scholar
Cassani, D. and Zhang, J., A priori estimates and positivity for semiclassical ground states for systems of critical Schrödinger equations in dimension two . Comm. Partial Differential Equations 42(2017), no. 5, 655–702.CrossRefGoogle Scholar
Clapp, M. and Pistoia, A., Symmetries, Hopf fibrations and supercritical elliptic problems . In: Mathematical congress of the Americas, Contemporary Mathematics, 656, American Mathematical Society, Providence, RI, 2016, pp. 1–12.Google Scholar
Clapp, M. and Soares, M., Energy estimates for seminodal solutions to an elliptic system with mixed couplings . NoDEA Nonlinear Differential Equations Appl. 30(2023), no. 11, 33 pp.CrossRefGoogle Scholar
Cowan, C., Liouville theorems for stable Lane–Emden systems and biharmonic problems . Nonlinearity 26(2013), 2357.CrossRefGoogle Scholar
Cowan, C. and Moameni, A., Supercritical elliptic problems on nonradial domains via a nonsmooth variational approach . J. Differential Equations 341(2022), 292–323.CrossRefGoogle Scholar
Cowan, C. and Moameni, A., On supercritical elliptic problems: Existence, multiplicity of positive and symmetry breaking solutions . Mathematische Annalen (2023). https://doi.org/10.1007/s00208-023-02685-9 CrossRefGoogle Scholar
de Figueiredo, D. G., Semilinear elliptic systems: Existence, multiplicity, symmetry of solutions . In: Handbook of differential equations: Stationary partial differential equations. Vol. V, Handbook of Differential Equations, Elsevier/North-Holland, Amsterdam, 2008, pp. 1–48.Google Scholar
de Figueiredo, D. G., Peral, I., and Rossi, J. D., The critical hyperbola for a Hamiltonian elliptic system with weights . Ann. Mat. Pura Appl. (4) 187(2008), 531–545.CrossRefGoogle Scholar
Gilbarg, D. and Trudinger, N. S., Elliptic partial differential equations of second order, Springer, Berlin, 2001.CrossRefGoogle Scholar
Lange Ferreira Melo, J. and Moreira dos Santos, E., Critical and noncritical regions on the critical hyperbola . In: Contributions to nonlinear elliptic equations and systems, 86, Progress in Nonlinear Differential Equations and Their Applications, Birkhäuser/Springer, Cham, 2015, pp. 345–370.CrossRefGoogle Scholar
Li, Y. Y., Existence of many positive solutions of semilinear elliptic equations on annulus . J. Differential Equations 83(1990), 348–367.CrossRefGoogle Scholar
Lieb, E. H., Sharp constants in the Hardy–Littlewood–Sobolev and related inequalities . Ann. Math. 118(1983), 349–374.CrossRefGoogle Scholar
Liu, F. and Yang, J., Nontrivial solutions of Hardy–Hénon type elliptic systems . Acta Math. Sci. Ser. B Engl. Ed. 27(2007), no. 4, 673–688.Google Scholar
Lou, Z., Weth, T., and Zhang, Z., Symmetry breaking via Morse index for equations and systems of Hénon–Schrödinger type . Z. Angew. Math. Phys. 70(2019), 35, 19 pp.CrossRefGoogle Scholar
Mitidieri, E., A Rellich type identity and applications . Comm. Partial Differential Equations 18(1993), nos. 1–2, 125–151.CrossRefGoogle Scholar
Moameni, A., Critical point theory on convex subsets with applications in differential equations and analysis . J. Math. Pures Appl. (9) 141(2020), 266–315.CrossRefGoogle Scholar
Pacella, F., Symmetry results for solutions of semilinear elliptic equations with convex nonlinearities . J. Funct. Anal. 192(2002), 271–282.CrossRefGoogle Scholar
Phan, Q. H., Liouville-type theorems and bounds of solutions for Hardy–Hénon elliptic systems . Adv. Differential Equations 17(2012), nos. 7–8, 605–634.CrossRefGoogle Scholar
Ruf, B., Superlinear elliptic equations and systems . In: Handbook of differential equations: Stationary partial differential equations. Vol. V, Handbook of Differential Equations, Elsevier/North-Holland, Amsterdam, 2008, pp. 211–276.CrossRefGoogle Scholar
Smets, D., Su, J., and Willem, M., Non radial ground states for the Hénon equation . Commun. Contemp. Math. 4(2002), 467–480.CrossRefGoogle Scholar
Smets, D. and Willem, M., Partial symmetry and asymptotic behavior for some elliptic variational problems . Calc. Var. Partial Differential Equations 18(2003), 57–75.CrossRefGoogle Scholar
Souplet, P., The proof of the Lane–Emden conjecture in four space dimensions . Adv. Math. 221(2009), no. 5, 1409–1427.CrossRefGoogle Scholar
Stein, E. M. and Weiss, G., Fractional integrals on $n$ -dimensional Euclidean space . J. Math. Mech. 7(1958), 503–514.Google Scholar
Szulkin, A., Minimax principles for lower semicontinuous functions and applications to nonlinear boundary value problems . Ann. Inst. H. Poincaré Anal. Non Linéaire 3(1986), no. 2, 77–109.CrossRefGoogle Scholar
Van der Vorst, R. C. A. M., Variational identities and applications to differential systems . Arch. Rational Mech. Anal. 116(1992), no. 4, 375–398.CrossRefGoogle Scholar
Wang, X.-J., Sharp constant in a Sobolev inequality . Nonlinear Anal. 20(1993), no. 3, 261–268.CrossRefGoogle Scholar