No CrossRef data available.
Article contents
SUMMABILITY AND ASYMPTOTICS OF POSITIVE SOLUTIONS OF AN EQUATION OF WOLFF TYPE
Part of:
Nonlinear integral equations
Functional analytic methods in summability
Qualitative behavior
Published online by Cambridge University Press: 14 May 2024
Abstract
We use potential analysis to study the properties of positive solutions of a discrete Wolff-type equation 
$$ \begin{align*} w(i)=W_{\beta,\gamma}(w^q)(i), \quad i \in \mathbb{Z}^n. \end{align*} $$
Here, 
$n \geq 1$,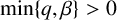 
$\min \{q,\beta \}>0$, 
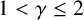$1<\gamma \leq 2$ and 
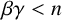$\beta \gamma <n$. Such an equation can be used to study nonlinear problems on graphs appearing in the study of crystal lattices, neural networks and other discrete models. We use the method of regularity lifting to obtain an optimal summability of positive solutions of the equation. From this result, we obtain the decay rate of 
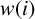$w(i)$ when 
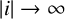$|i| \to \infty $.
MSC classification
Primary:
45M20: Positive solutions
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.
References
Cascante, C., Ortega, J. and Verbitsky, I., ‘Nonlinear potentials and two-weight trace inequalities for general dyadic and radial kernels’, Indiana Univ. Math. J. 53 (2004), 845–882.CrossRefGoogle Scholar
Chen, W., Jin, C., Li, C. and Lim, J., ‘Weighted Hardy–Littlewood–Sobolev inequalities and systems of integral equations’, Discrete Contin. Dyn. Syst. 2005(supplement) (2005), 164–172.Google Scholar
Chen, W. and Li, C., Methods on Nonlinear Elliptic Equations, Differential Equations and Dynamical Systems, 4 (American Institute of Mathematical Sciences, Springfield, MO, 2010).Google Scholar
Chen, W. and Li, C., ‘Radial symmetry of solutions for some integral systems of Wolff type’, Discrete Contin. Dyn. Syst. 30 (2011), 1083–1093.CrossRefGoogle Scholar
Chen, W., Li, C. and Ou, B., ‘Qualitative properties of solutions for an integral equation’, Discrete Contin. Dyn. Syst. 12 (2005), 347–354.CrossRefGoogle Scholar
Chen, X. and Zheng, X., ‘Optimal summation interval and nonexistence of positive solutions to a discrete system’, Acta Math. Sci. Ser. B (Engl. Ed.) 34 (2014), 1720–1730.Google Scholar
, W. E and Li, D., ‘On the crystallization of 2D hexagonal lattices’, Comm. Math. Phys. 286 (2009), 1099–1140.CrossRefGoogle Scholar
Franca, M., ‘Classification of positive solutions of
$p$
-Laplace equation with a growth term’, Arch. Math. (Brno) 40 (2004), 415–434.Google Scholar
$p$
-Laplace equation with a growth term’, Arch. Math. (Brno) 40 (2004), 415–434.Google ScholarGassner, H., Probst, M., Lauenstein, A. and Hermansson, K., ‘Representation of intermolecular potential functions by neural networks’, J. Phys. Chem. A 102 (1998), 4596–4605.CrossRefGoogle Scholar
Hedberg, L. I. and Wolff, T., ‘Thin sets in nonlinear potential theory’, Ann. Inst. Fourier (Grenoble) 33 (1983), 161–187.CrossRefGoogle Scholar
Hua, B. and Li, R., ‘The existence of extremal functions for discrete Sobolev inequalities on lattice graphs’, J. Differential Equations 305 (2021), 224–241.CrossRefGoogle Scholar
Huang, G., Li, C. and Yin, X., ‘Existence of the maximizing pair for the discrete Hardy–Littlewood–Sobolev inequality’, Discrete Contin. Dyn. Syst. 35 (2015), 935–942.CrossRefGoogle Scholar
Jin, C. and Li, C., ‘Qualitative analysis of some systems of integral equations’, Calc. Var. Partial Differential Equations 26 (2006), 447–457.CrossRefGoogle Scholar
Kawano, N., Yanagida, E. and Yotsutani, S., ‘Structure theorems for positive radial solutions to
$\operatorname{div}(|{Du|}^{m-2} Du)+K(|x|){u}^q=0$
in
${\mathbb{R}}^n$
’, J. Math. Soc. Japan 45 (1993), 719–742.CrossRefGoogle Scholar
$\operatorname{div}(|{Du|}^{m-2} Du)+K(|x|){u}^q=0$
in
${\mathbb{R}}^n$
’, J. Math. Soc. Japan 45 (1993), 719–742.CrossRefGoogle ScholarKilpelaiinen, T. and Maly, J., ‘The Wiener test and potential estimates for quasilinear elliptic equations’, Acta Math. 172 (1994), 137–161.CrossRefGoogle Scholar
Labutin, D., ‘Potential estimates for a class of fully nonlinear elliptic equations’, Duke Math. J. 111 (2002), 1–49.CrossRefGoogle Scholar
Lei, Y. and Li, C., ‘Sharp criteria of Liouville type for some nonlinear systems’, Discrete Contin. Dyn. Syst. 36 (2016), 3277–3315.CrossRefGoogle Scholar
Lei, Y., Li, C. and Ma, C., ‘Asymptotic radial symmetry and growth estimates of positive solutions to weighted Hardy–Littlewood–Sobolev system’, Calc. Var. Partial Differential Equations 45 (2012), 43–61.CrossRefGoogle Scholar
Lei, Y., Li, Y. and Tang, T., ‘Critical conditions and asymptotics for discrete systems of the Hardy–Littlewood–Sobolev type’, Tohoku Math. J. (2) 75 (2023), 305–328.CrossRefGoogle Scholar
Lieb, E., ‘Sharp constants in the Hardy–Littlewood–Sobolev and related inequalities’, Ann. of Math. (2) 118 (1983), 349–374.CrossRefGoogle Scholar
Liu, S., ‘Regularity, symmetry, and uniqueness of some integral type quasilinear equations’, Nonlinear Anal. 71 (2009), 1796–1806.CrossRefGoogle Scholar
Ma, C., Chen, W. and Li, C., ‘Regularity of solutions for an integral system of Wolff type’ Adv. Math. 226 (2011), 2676–2699.CrossRefGoogle Scholar
Phuc, N. and Verbitsky, I., ‘Quasilinear and Hessian equations of Lane–Emden type’, Ann. of Math. (2) 168 (2008), 859–914.CrossRefGoogle Scholar
Serrin, J. and Zou, H., ‘Cauchy–Liouville and universal boundedness theorems for quasilinear elliptic equations and inequalities’, Acta Math. 189 (2002), 79–142.CrossRefGoogle Scholar
Sun, S. and Lei, Y., ‘Fast decay estimates for integrable solutions of the Lane–Emden type integral systems involving the Wolff potentials’, J. Funct. Anal. 263 (2012), 3857–3882.CrossRefGoogle Scholar