Article contents
GALOIS LCD CODES OVER 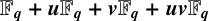 $\boldsymbol {\mathbb {F}_q+u\mathbb {F}_q+v\mathbb {F}_q+uv\mathbb {F}_q}$
$\boldsymbol {\mathbb {F}_q+u\mathbb {F}_q+v\mathbb {F}_q+uv\mathbb {F}_q}$
Published online by Cambridge University Press: 15 December 2022
Abstract
Wu and Shi [‘A note on k-Galois LCD codes over the ring
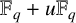 $\mathbb {F}_q + u\mathbb {F}_q$
’, Bull. Aust. Math. Soc. 104(1) (2021), 154–161] studied
$\mathbb {F}_q + u\mathbb {F}_q$
’, Bull. Aust. Math. Soc. 104(1) (2021), 154–161] studied
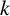 $ k $
-Galois LCD codes over the finite chain ring
$ k $
-Galois LCD codes over the finite chain ring
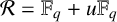 $\mathcal {R}=\mathbb {F}_q+u\mathbb {F}_q$
, where
$\mathcal {R}=\mathbb {F}_q+u\mathbb {F}_q$
, where
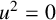 $u^2=0$
and
$u^2=0$
and
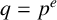 $ q=p^e$
for some prime p and positive integer e. We extend the results to the finite nonchain ring
$ q=p^e$
for some prime p and positive integer e. We extend the results to the finite nonchain ring
 $ \mathcal {R} =\mathbb {F}_q+u\mathbb {F}_q+v\mathbb {F}_q+uv\mathbb {F}_q$
, where
$ \mathcal {R} =\mathbb {F}_q+u\mathbb {F}_q+v\mathbb {F}_q+uv\mathbb {F}_q$
, where
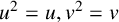 $u^2=u,v^2=v $
and
$u^2=u,v^2=v $
and
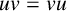 $ uv=vu $
. We define a correspondence between the
$ uv=vu $
. We define a correspondence between the
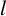 $ l $
-Galois dual of linear codes over
$ l $
-Galois dual of linear codes over
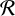 $ \mathcal {R} $
and the
$ \mathcal {R} $
and the
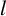 $ l $
-Galois dual of their component codes over
$ l $
-Galois dual of their component codes over
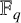 $ \mathbb {F}_q $
. Further, we construct Euclidean LCD and
$ \mathbb {F}_q $
. Further, we construct Euclidean LCD and
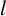 $ l $
-Galois LCD codes from linear codes over
$ l $
-Galois LCD codes from linear codes over
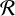 $ \mathcal {R} $
. We prove that any linear code over
$ \mathcal {R} $
. We prove that any linear code over
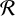 $ \mathcal {R} $
is equivalent to a Euclidean code over
$ \mathcal {R} $
is equivalent to a Euclidean code over
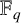 $\mathbb {F}_q$
with
$\mathbb {F}_q$
with
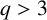 $ q>3 $
and an
$ q>3 $
and an
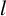 $ l $
-Galois LCD code over
$ l $
-Galois LCD code over
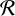 $ \mathcal {R}$
with
$ \mathcal {R}$
with
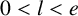 $0<l<e$
and
$0<l<e$
and
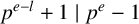 $p^{e-l}+1\mid p^e-1$
. Finally, we investigate MDS codes over
$p^{e-l}+1\mid p^e-1$
. Finally, we investigate MDS codes over
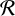 $ \mathcal {R}$
.
$ \mathcal {R}$
.
MSC classification
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.
Footnotes
The first and second authors are supported by UGC, New Delhi, Govt. of India under grant DEC18-417932 and CSIR, New Delhi, Govt. of India under F. No. 09/086(1407)/2019-EMR-I, respectively.
References
- 1
- Cited by





