No CrossRef data available.
Article contents
AN IMPROVEMENT TO A THEOREM OF LEONETTI AND LUCA
Part of:
Sequences and sets
Published online by Cambridge University Press: 01 September 2023
Abstract
Leonetti and Luca [‘On the iterates of the shifted Euler’s function’, Bull. Aust. Math. Soc., to appear] have shown that the integer sequence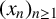 
$(x_n)_{n\geq 1}$ defined by 
$x_{n+2}=\phi (x_{n+1})+\phi (x_{n})+k$, where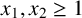 
$x_1,x_2\geq 1$, 
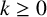$k\geq 0$ and 
$2 \mid k$, is bounded by 
$4^{X^{3^{k+1}}}$, where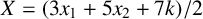 
$X=(3x_1+5x_2+7k)/2$. We improve this result by showing that the sequence 
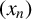$(x_n)$ is bounded by 
$2^{2X^2+X-3}$, where 
$X=x_1+x_2+2k$.
MSC classification
Secondary:
11B37: Recurrences
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.
Footnotes
Nguyen Xuan Tho is funded by the Vietnam Ministry of Education and Training under the project number B2022-CTT-03.
References
Aigner, M. and Ziegler, G. M., Proofs from The Book, 6th edn (Springer, Berlin, 2018).CrossRefGoogle Scholar
Erdős, P., ‘Beweis eines Satzes von Tschebyschef’, Acta Sci. Math. (Szeged) 5 (1930–1932), 194–198.Google Scholar
Leonetti, P. and Luca, F., ‘On the iterates of the shifted Euler’s function’, Bull. Aust. Math. Soc., to appear. Published online (12 May 2023).CrossRefGoogle Scholar
Rosser, J. B., ‘The
$n$
-th prime is greater than
$n \log n$
’,
Proc. Lond. Math. Soc. (3) 45 (1939), 21–44.CrossRefGoogle Scholar
$n$
-th prime is greater than
$n \log n$
’,
Proc. Lond. Math. Soc. (3) 45 (1939), 21–44.CrossRefGoogle Scholar